Данный урок является первым из двух уроков, которые отводятся на изучение темы «Графики функций у=ах2+п и у=а(х-т)2» Преподавание ведётся по учебнику « Алгебра, 9», Ю.Н. Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б. Суворова. Данная тема включена в главу «Квадратичная функция». Изучение квадратичной функции начинается с рассмотрения функции у=ах2, её свойств и особенностей графика, а уже затем рассматриваются частные виды у=ах2+п и у=а(х-т)2.Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы учащиеся понимали, что график функции у=ах2+bx+c может быть получен из графика функции у=х2 с помощью соответствующих преобразований относительно осей координат.
| Содержание урока | Деятельность учителя | Деятельность учащихся |
Оргмомент Цель: подготовка учащихся к работе на уроке |
|
| Приветствует учащихся, выясняет отсутствующих. | Приветствуют учителя.
|
Проверка домашнего задания Цель: - проверка правильности выполнения задания; |
| № 102. Площадь поверхности куба у (см2) зависит от ребра куба х (см). Задайте эту зависимость формулой. Постройте ее график и найдите по графику: а) поверхность куба, если его ребро равно 0,9 см; 1,5 см; 1,8 см; б) длину ребра, если поверхность куба равна 7 см2; 10 см2; 14 см2; | Выясняет: | Называют причины затруднений при выполнении задания. Возможные затруднения: при нахождении ординат точек пересечения; при построении графиков заданных функций Проверяют правильность решения задачи по предложенному образцу.
|
Постановка цели урока. Устная работа. Цель: -актуализация опыта учащихся по данной теме; -подготовка учащихся к усвоению нового материала; -организация целенаправленной познавательной деятельности учащихся. |
|
| Сегодня на уроке мы обобщим накопленные знания о квадратичной функции. С одним из видов которой вы знакомы - это функция у = ах2, и рассмотрим квадратичную функцию вида у = ах2 + Ьх + с.
| Ответы: * Некоторые математические величины связаны зависимостью у = ах2, например, площадь круга от его радиуса.
|
|
| Вопрос: Сколько необходимо задать точек, чтобы построить график функции у=ах2?
| Ответы: - составить таблицу значений из 5-7 точек, симметричных относительно оси у; - вершину О(0;0) и еще 2-3 точки на одной из ветвей параболы. |
|
| Вопрос: Как с помощью графика у=х2 построить: а) у=2х2; б) у = 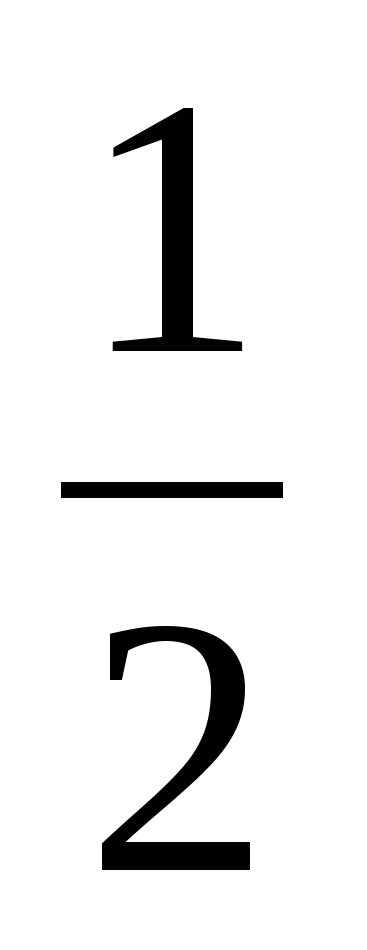 х2; х2; в) у= -2х2 Учитель на доске демонстрирует соответствующие преобразования а) графика функции у=х2 в у=2х2
б) графика функции у=х2 в у=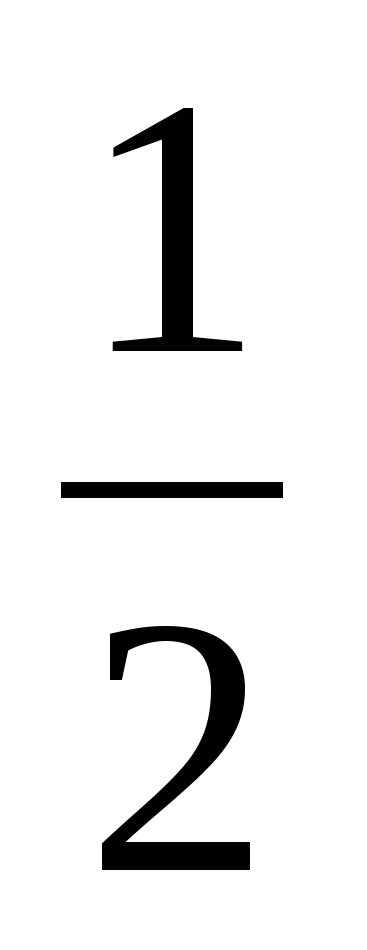 х2 х2
в) графика функции у=2х2 в у= -2х2
|
Ответы:
График функции у = af(x) можно получить из графика функции у = f(х) с помощью растяжения от оси х в а раз, если а 1, и с помощью сжатия к оси х в 1/а раз, если 0 а
График функции у = -f(x) можно получить из графика функции у=f(х) с помощью симметрии относительно оси х.
|
Работа с классом Цель: - развивать умение обобщать, классифицировать, строить умозаключения, делать выводы; - воспитание культуры коллективной работы. |
|
| Учитель. Как построить график функции у=ах2+bx+c с заданными коэффициентами?
Постройте график функции заданной формулой у = х2 - 4 Какую кривую представляет построенный график?
| Ответ. Взять достаточно большое количество точек.
Учащиеся пытаются построить график заданной функции. Параболу.
|
|
| Учитель. Обратите внимание на расположение парабол. Запишите на листе все вопросы, которые возникают при исследовании зависимости между расположением параболы и функцией.
| Через 4-5мин слушаем ответы. Некоторые вопросы, которые задают учащиеся: От чего зависит расположение вершины параболы? Что может влиять на вид параболы? В каких случаях парабола пересекает ось абсцисс, касается ее или не пересекает? Сколько достаточно знать точек, чтобы построить график любой квадратичной функции?
|
| Таблица 1 | х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | | у | -4,5 | -2 | -0,5 | 0 | -0,5 | -2 | -4,5 |
Таблица 2 | х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | | у | -0,5 | 2 | 3,5 | 4 | 3,5 | 2 | -0,5 |
|
Учитель. Рассмотрим исследование функции у=ах2+bх+с на примере № 106 а) у = - 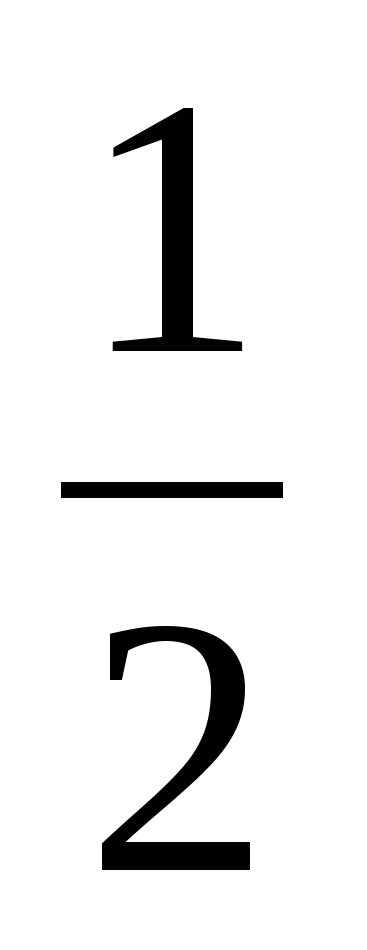 х2 + 4 х2 + 4 Сравним таблицы значений для функций у= - 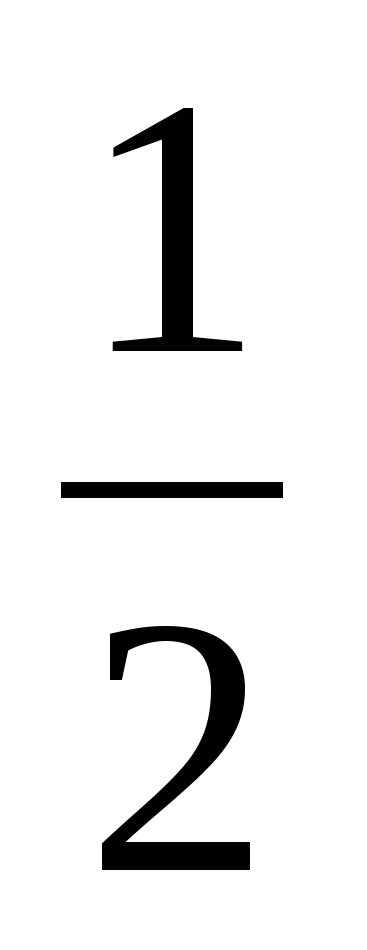 х2 и у= - х2 и у= - 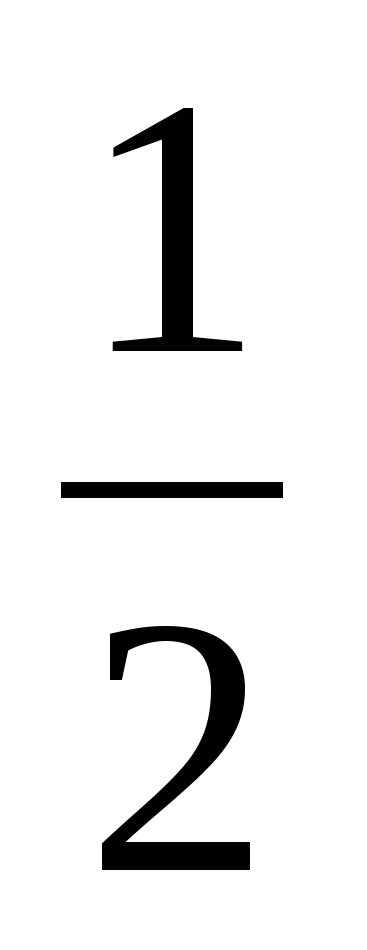 х2 + 4. х2 + 4.
|
Учащиеся заполняют таблицы (один ученик работает у доски), сравнивают полученные значения и делают вывод, что для любого значения х значение второй функции на 4 единиц больше соответствующего значения первой. Значит, график второй функции есть также парабола, полученная переносом графика первой функции вверх параллельно оси ординат на 4 единиц.
|
|
| Учитель с помощью доски демонстрирует параллельный перенос.
Учитель предлагает учащимся построить график функции у= - 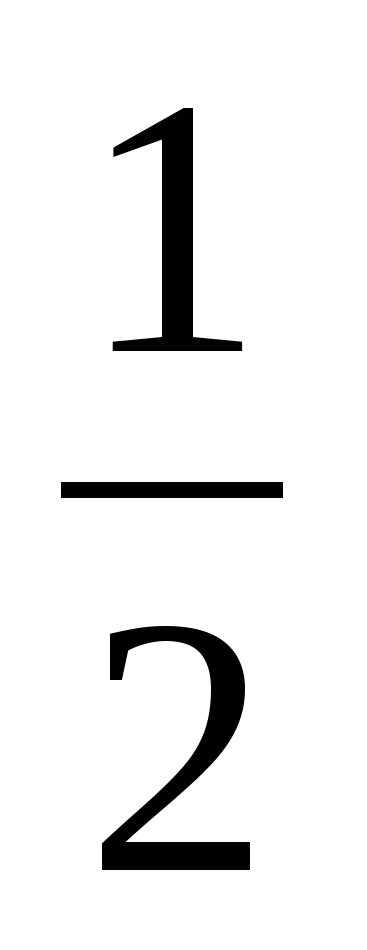 х2-3 х2-3 | Учащиеся выполняют построение в тетрадях с помощью шаблонов.
Учащиеся выполняют построение в тетрадях с помощью шаблонов, в той же координатной плоскости. |
- Какова область определения функции? - Какова область значений функции? Указать промежутки возрастания и убывания функции. Какая прямая является осью симметрии функции? Чему равно наименьшее значение функции?
| Учитель предлагает учащимся ответить на вопросы, записанные на классной доске.
| Учащиеся отвечают на вопросы, сравнивают свойства функций.
Делают вывод: график функции у = ах2 + n является параболой, которую можно получить из графика функции у = ах2 с помощью параллельного переноса вдоль оси у на n единиц вверх, если n 0, или на n единиц вниз, если n
|
|
Таблица 1. | х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | | у | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Таблица 3.
| х | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | у | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| Учитель. Теперь рассмотрим функцию у=(х-5)2.Для этого в одной системе координат построим графики функций у= х2 и у=(х-5)2.Таблица значений для первой функции заполнена, составим таблицу значений второй функции. При этом в качестве значений аргумента выберем те, которые на 5 больше соответствующих значений аргумента в таблице 1. | Учащиеся заполняют таблицу(один ученик у доски) и замечают, что значения аргумента изменились, а соответствующие значения функции те же, что и записанные во второй строке таблицы 1.
|
|
| Учитель с помощью доски демонстрирует параллельный перенос или предлагает это сделать учащимся
| Далее учащиеся строят график, отметив точки, координаты которых указанные в таблице 3. Один ученик выполняет построение на доске. Замечают, что если переместить каждую точка графика функции у=х2 на 5 единицы вправо, то получим график функции у=(х-5)2.
Учащиеся отвечают на вопросы, сравнивают свойства функций.
|
|
| Учитель предлагает учащимся построить график функции у=(х+3)2 | Учащиеся делают вывод: график функции у =а(х-т)2 является параболой, которую можно получить из графика функции у = ах2 с помощью параллельного переноса вдоль оси х на т единиц вправо, если т о, или на т единиц влево, если т
|
| 6.Закрепление полученных знаний.
|
| № 109(а,г) | Учитель координирует действия учащихся, помогает проговаривать и обосновывать выполняемые преобразования | Учащиеся выполняют преобразования в тетрадях с помощью шаблонов, розданных учителем. По очереди выполняют преобразования на доске. |
| 7. Самостоятельная работа Цель: -формировать умения по заданной формуле строить графики функций у = ах2 + n и у =а(х-т)2 |
| Самостоятельная работа. Используя шаблон параболы у = х2, постройте график функции: а) у = - х2 + 3, б) у = (х – 2)2, в) у = - х2 – 4. | Учитель консультирует тех учащихся, которые затрудняются при выполнении задания, выбирает помощников –консультантов из числа справившихся с заданием. Демонстрирует правильное решение(к каждому графику подвигаем соответствующую формулу) | Учащиеся выполняют работу в тетрадях. Помощники - консультанты помогают затрудняющимся |
| 8. Подведение итогов.
|
| Домашнее задание:п.6, № 106( б, в), 111 (а). | Учитель обращается к учащимися с просьбой проговорить изученные правила построения графиков. Задает домашнее задание | Учащиеся проговаривают основные правила преобразований графиков и записывают домашнее задание. |
















