Республика КАЗАХСТАН, г.Кызылорда
средняя школа № 173 имени Алии Молдагуловой
учитель математики высшей категории
Шайхутдинова Галия Жагфаровна
Класс: 8
Интергрированный урок информатики и математики
Тема: Графики квадратичных функций y=ax2+n и y=a(x-m)2
Цель: способствовать формированию навыков применения простейших преобразований для построения графиков функций
Задачи:
- освоить возможности построения графиков функций в программе Graphics;
-создать условия для развития исследовательской культуры обучающихся;
-способствовать развитию логического мышления;
-воспитывать интерес к предмету.
Оборудование: компьютеры Pentium IV, графическая программа Graphics, доска, шаблон
парабол.
I. Организационный момент. Проверка готовности обучающихся к уроку, наличия и функциональности необходимого ПО.
II. Актуализация и коррекция опорных знаний
1. фронтальная устная работа:
а) какая функция называется квадратичной?
б) от чего зависит направление ветвей функции y=ax2?
в) что является графиком квадратичной функции?
г) в какой точке находится вершина параболы?
д) перечислить свойства функции y=ax2 для a>0, a<0.
е) выполнить проверку ответов, сравнивая их с опорным конспектом, представленным на доске.
|
a>0 |
|
a<0 |
|
1. D(y)=(-∞;+∞( |
|
1. D(y)=(-∞;+∞( |
|
2. Если х=0, то y=0. Вершина находится в точке О(0;0). |
|
2. Если х=0, то y=0. Вершина находится в точке О(0;0). |
|
3. При х≠0, у>0. График расположен в верхней полуплоскости, ветви направлены вверх. |
|
3. При х≠0, у<0. График расположен в нижней полуплоскости, ветви направлены вниз. |
|
4. График симметричен относительно оси У. |
|
4. График симметричен относительно оси У. |
|
5. Функция убывает при хÎ(-∞;0]. Функция возрастает при хÎ[0;+∞). |
|
5. Функция возрастает при хÎ(-∞;0]. Функция убывает при хÎ[0;+∞). |
|
6. Наименьшее зачение xmin=0 ymin=0. |
|
6. Наибольшее зачение xmax=0 ymax=0. |
|
7. E(y)=[0;+∞). |
|
7. E(y)=(-∞;0]. |
2. Проверка домашнего задания.
Сравнить полученные ответы с результатом, указанным на доске. Найти ошибки
№ 505 - 1) х=-1,5, у=-4,5; х=0,6, у=0,42; х=1,5, у=-4,5.
2)У=-1, х=±0,7, у=-3, х=±1,3, у=-4,5, х=±1,5.
№ 507 - E(y)=[0;+∞); E(y)=(-∞; 0].
Результаты проверки обсуждаются с обучающимися.
III. Изучение нового материала
- Целеполагание, мотивация учебной деятельности
Учитель: сегодня мы рассмотрим частные случаи графиков квадратичной функции у=ах2+bx+c, пронаблюдаем за изменениями графика функции и сделаем вывод.
Мы будем строить y=ax2+n, где n-любое число, и y=a(x-m)2, где m-любое число.
Алгоритм работы.
1. Занять рабочее место за компьютером, войти в учетную запись Гость. На рабочем столе найти ярлык программы Graphics, щелкнуть по нему. Развернуть открывшееся окно.
2. Работа с интерфейсом программы Graphics: щелкнуть по кнопке Сервис в строке меню программы. Выбрать в ниспадающем меню Сетка, цвет светло-серый, линия пунктирная щелкнуть кнопку ОК.
3. На Панели инструментов щелкнуть по кнопке Добавить график (или в Меню выбрать График Добавить график). Выбрать Цвет – синий, толщина линии 1,5 пикселя)
4. Следовать инструкции, указанной на карточке-задании.
IV. Исследование функций вида y=ax2+n и y=a(x-m)2
Задание 1.
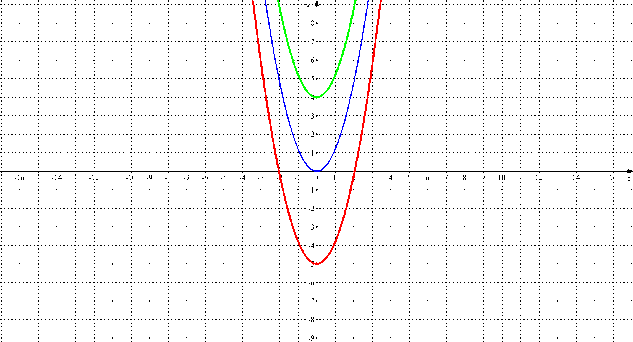
а) В одной системе координат построить графики функций: у=1,2х2 , у=1,2х2+4, у=1,2х2-5, используя программу Graphics.
б) Указать координаты вершин парабол ( О(0;0), О’(0;4), O’’(0;-5)).
в) Сделать вывод о взаимном расположении графиков. Высказать гипотезу о способе получения графиков функций у=1,2х2+4 и у=1,2х2-5. ( Графики функций у=1,2х2+4 и у=1,2х2-5 получены из графика функции у=1,2х2 параллельным переносом вдоль оси ОУ на 4 ед. вверх и на 5 ед. вниз.)
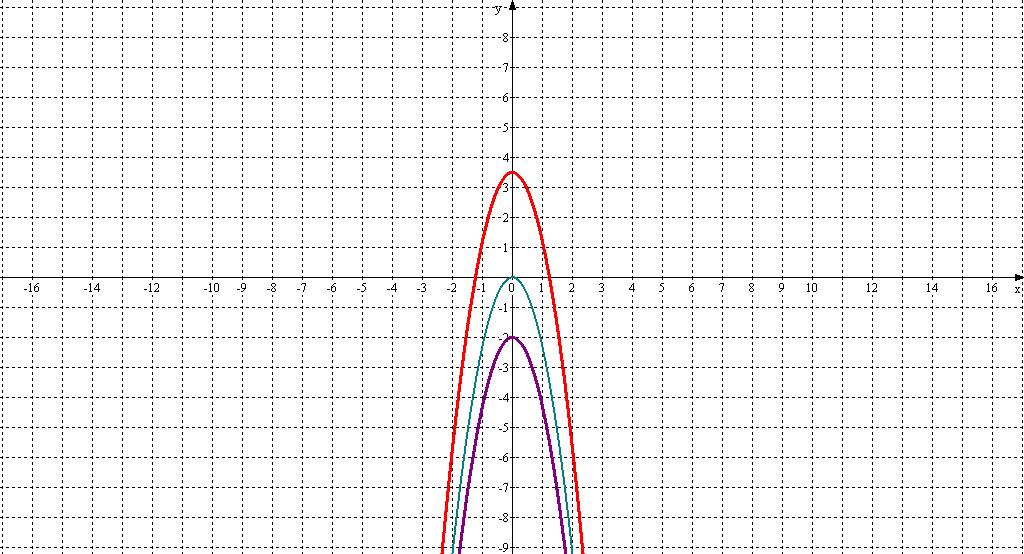
г). Построить графики у=-2,3х2, у=-2,3х2-2, у=-2,3х2+3,5. Проверить полученную гипотезу.
В тетради записывается вывод:
графиком y=ax2+n является парабола, которую можно получить из графика y=ax2 с помощью параллельного переноса на n единиц вдоль оси У. Если n>0, то вверх, если n<0, то вниз.
Задание 2.
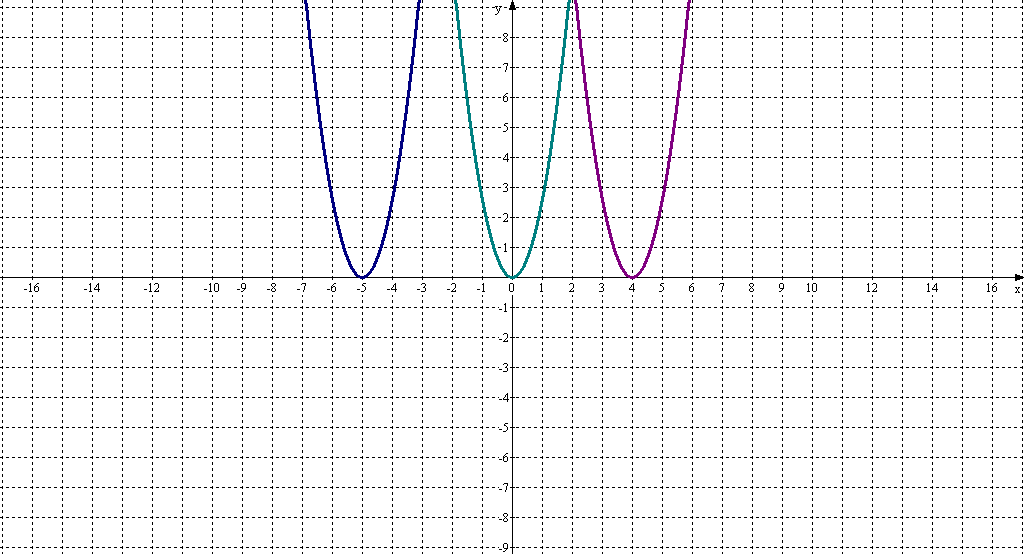
а) В одной системе координат построить графики функций: у=2,6х2, у=2,6(х-4)2, у=2,6(х+5)2. б) Записать координаты вершины. ( О(0,0), O’(4;0), O’’(-5;0)).
в) Сделать вывод о взаимном расположении графиков. Высказать гипотезу о способе получения графиков функций у=2,6(х-4)2, у=2,6(х+5)2
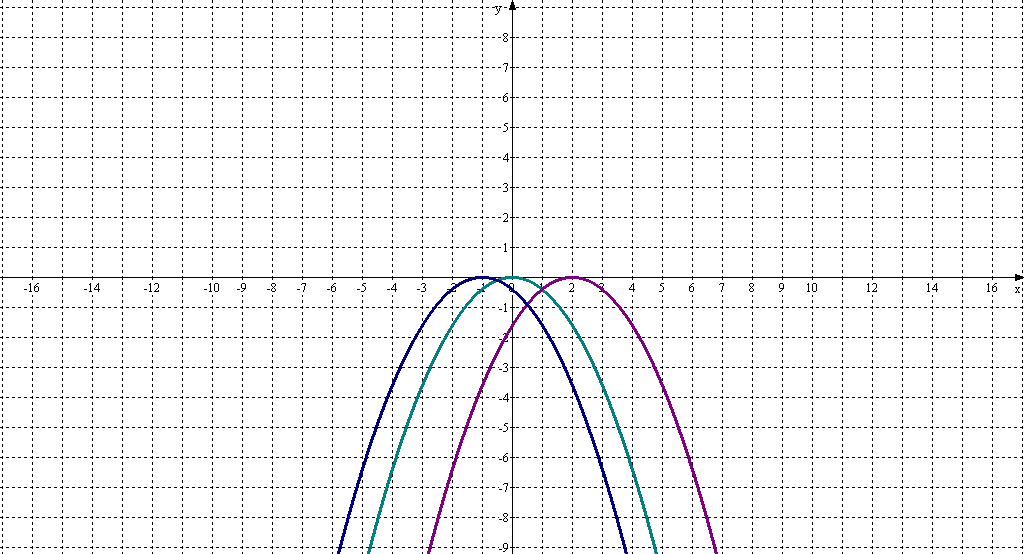
г) Проверить гипотезу, построив графики функций у=-0,4х2, у=-0,4(х-2)2, у=-0,4(х+1)2.
В тетради записывается вывод:
графиком функции y=a(x-m)2 является парабола, которую можно получить из y=ax2, с помощью параллельного переноса на m единиц вдоль оси ОХ. Если m>0, то вправо, если m<0, то влево.
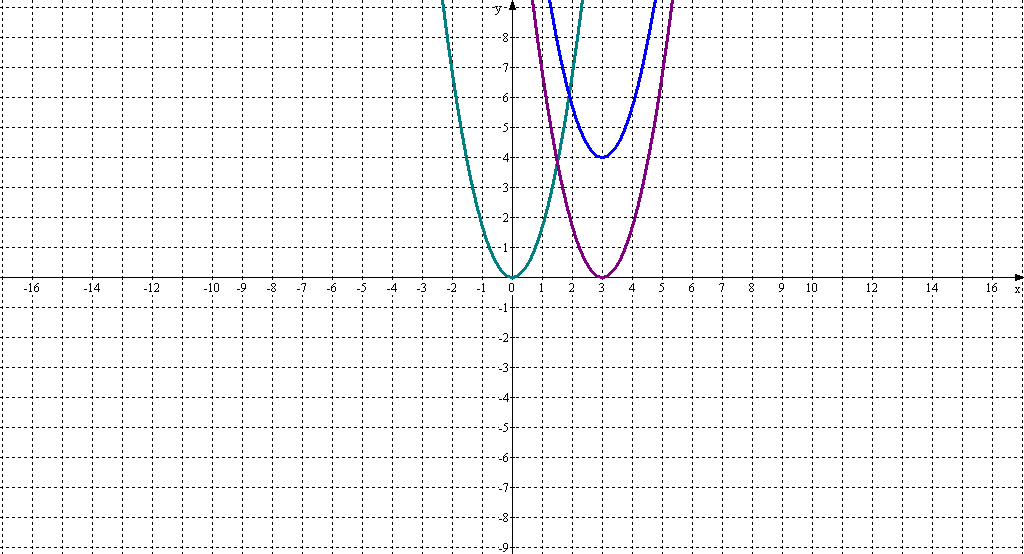
Задание 3. Построить график функции у=1,7(х-3)+4.
а) Разбить построение на этапы: у=1,7х2, у=1,7(х-3)2, у=1,7(х-3)2+4. П
б) пронаблюдать за перемещениями вершины параболы. (Вершина перемещалась вправо на 3 единицы по оси ОХ, а затем вверх на 4 единицы по оси ОУ).
Вывод: график у = а (х - m)2 + n является параболой, которую можно получить из у=ах2 параллельным переносом вдоль оси х на m единиц и вдоль оси у на n единиц.
Задание 5. Построить на доске, используя шаблон, график функции у=(х+4)2-2.
V. Рефлексия. Используя методику «Я, мы, дело», охарактеризовать качество проделанной на уроке работы, оценить степень удовлетворенности уроком.
- Домашнее задание: п. 21, № 518 (а, б)