Тема «Решение простейших тригонометрических уравнений»
Цели занятия:
Образовательная:
- Вывести формулы решения простейших тригонометрических уравнений.
- Сформировать у студентов первичные умения и навыки решения простейших тригонометрических уравнений.
Развивающая:
- Развивать математическое мышление.
- Умение наблюдать, сравнивать, обобщать и анализировать математические ситуации.
Воспитательная:
- Воспитывать активность, самостоятельность, упорство и достижение цели.
Тип занятия: комбинированный.
Обеспечение занятия:
Наглядные пособия: таблицы значений тригонометрических функций, сводные таблицы решения тригонометрических уравнений.
ТСО: компьютер, интерактивная доска.
Оснащение ТСО: программа Microsoft office PowerPoint.
Вычислительные средства: микрокалькуляторы, таблицы значений тригонометрических функций.
Междисциплинарные связи: физика, информатика, геодезия, техническая механика, геофизика, гидрогеология.
Ход занятия:
- Организационный момент:
Проверка отсутствующих, заполнение журнала.
Постановка темы и целей урока.
- Проверка знаний:
Фронтальный опрос (устные вопросы слайд №2)
- Дайте определение функции . Назовите ее область определения и область значения.
- Чему равен ?
- Сформулируйте определение арккосинуса числа.
- Чему равен ?
- Дайте определение функции . Назовите область определения и область значения этой функции.
- Чему равен ?
- Дайте определение арккотангенса числа.
- Чему равен ?
Устный счет по таблицам значения тригонометрических функций:
Проверка домашней работы:
Студентам предлагается исправить ошибки решенной на доске домашней работы и сделать соответствующие комментарии. (6 человек по 1 примеру)
Домашняя работа на доске с ошибками:
Верное решение:
Остальные студенты сверяют решение домашнего задания по своим тетрадям.
- Объяснение нового материала:
Актуализация опорных знаний:
Обратные тригонометрические функции необходимы нам для изучения новой темы «Решение простейших тригонометрических уравнений»,
так как они используются при решении тригонометрических уравнений.
В курсе алгебры вы уже встречались с различными видами уравнений. Давайте вспомним какие это уравнения?
Предполагаемый ответ: линейные, квадратные, кубические, логарифмические, показательные, иррациональные.
Сегодня мы с вами познакомимся с тригонометрическими уравнениями.
Это не последние уравнения в математике, например, на втором курсе мы начнем решать дифференциальные уравнения.
3.1 (Слайд № 3: Определение и виды простейших тригонометрических уравнений)
Давайте запишем определение тригонометрического уравнения.
Тригонометрическим называется уравнение, содержащие переменную под знаком тригонометрической функции.
Сегодня мы рассмотрим решение простейших из них:
Решить тригонометрическое уравнение – это значит найти все его корни.
Корнем тригонометрического уравнения называется такое значение входящей в него переменной, которая удовлетворяет этому уравнению.
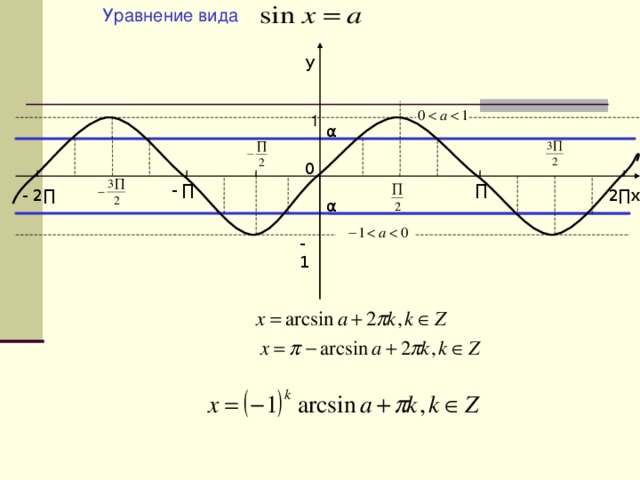
- (Слайд №4: Уравнение вида )
Рассмотрим уравнение вида .
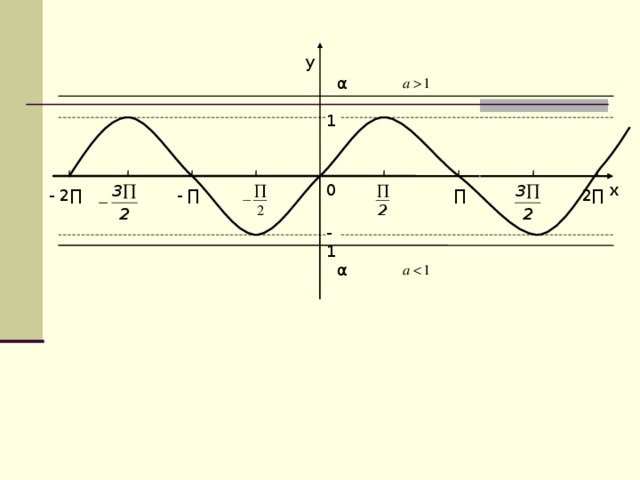
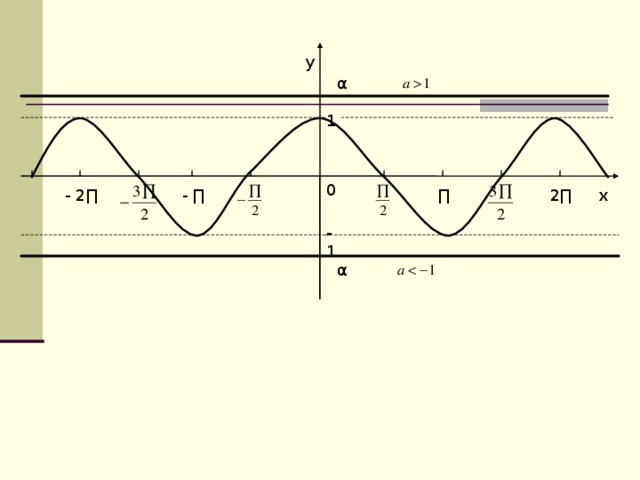
Так как , то уравнение при и не имеет решений.
Период синуса равен , поэтому достаточно найти все решения этого уравнения на любом отрезке длины . Из рисунка видно что, что на отрезке синус возрастает и принимает каждое свое значение один раз. Следовательно, на этом отрезке . На отрезке синус убывает и принимает каждое свое значение тоже один раз. Чтобы найти решение на этом отрезке, вспомним что . Если , то
, и поэтому решением уравнения на отрезке будет .
Для получения всех решений уравнения к каждому из двух полученных решений прибавим числа вида где .Следовательно,
Обе серии решений можно объединить:
называют параметром, при к четном получается формула (1), при к нечетном получается формула (2)
3.3 (Слайд № 5: Частные случаи уравнения . )
При а=1 уравнение имеет решения , .
При а=-1 уравнение имеет решения ,
При а=0 уравнение имеет решения , .
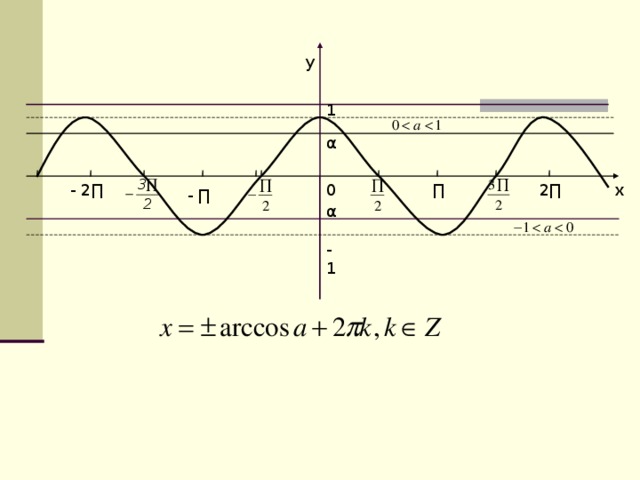
3.4Уравнение вида: (Слайд №6: уравнение вида: )
Рассмотрим уравнение . При и уравнение не имеет решений, так как .
Так как период косинуса равен , то при для нахождения всех решений достаточно рассмотреть отрезок длины . Удобнее всего выбрать отрезок . Очевидно, что уравнение на отрезке имеет решение , а на отрезке - решение так как функция косинус четная. Таким образом на отрезке уравнение имеет решения
Чтобы записать все решения уравнения необходимо, учитывая периодичность косинуса, прибавить к каждому из найденных значений по , где . В итоге получим бесконечное множество решений
3.5(Слайд №7: Частные случаи уравнения )
При а=1 уравнение имеет решения , .
При а= -1 уравнение имеет решения ,
При а=0 уравнение имеет решения , .
3.6 Уравнения вида: , (Слайд №8: уравнения вида: , : )
Так как период тангенса равен , то для того чтобы найти все решения уравнения , достаточно найти все его решения на любом отрезке длины . По определению арктангенса решение уравнения на промежутке есть .
Для того чтобы получить все решения уравнения нужно к решению, полученному на отрезке длины , прибавить . Следовательно,,
И решение уравнения
(Слайд № 9:Сводная таблица решения простейших тригонометрических уравнений)
Сводная таблица решения простейших тригонометрических уравнений
Уравнение
Общее решение
Частные случаи
Студенты заполняют сводную таблицу по ходу объяснения материала.
4.Обобщение и систематизация знаний:
Решение примеров у доски.
Решить уравнения:
Дополнительные задания:
- Подведение итогов занятия:
Сегодня мы с вами познакомились с формулами для решения простейших тригонометрических уравнений и закрепили их при решении задач. На следующем занятии мы рассмотрим более сложные тригонометрические уравнения и познакомимся с методами их решения. Активным студентам выставление оценок.
Домашнее задание: §28, решить примеры (Слайд№10: домашнее задание).
Примеры для домашнего задания.
Литература:
- Математика для техникумов. Алгебра и начала анализа: Учебник. Ч.1/ Под ред. Г.Н. Яковлева – М.: Наука, 1987 – 464с.
- Н.В. Богомолов Практические занятия по математике: Учеб. Пособие для средних спец. Заведений / Н.В. Богомолов – М.: Высшая школа, 2003-495с.