В конспекте урока повторения по теме"Гипербола"поставлены цели обобщения и закрепления знаний учеников по изученной теме с целью приобретения более глубоких знаний по математике курса 8 класса.Урок будет проходить в виде состязания двух команд по этапам.Ученики познакомятся с историческим значением слова "Гипербола" и в каком школьном предмете встречаются высказывания, в которых применяется преувеличение.Ученикам предстоит не только уметь определять положение графика в зависимости от коэффициента, но и уметь находить промежутки монотонности, составлять формулу графика в различных ситуациях.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Конспект урока в 8 классе "Гипербола"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«конспект урока гипербола в 8 классе»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1690 руб.
2820 руб.
1490 руб.
2480 руб.
1690 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
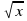 3) -8/х = х2 4) 9/х = х
3) -8/х = х2 4) 9/х = х















