Тема урока : «Высота, биссектриса и медиана треугольника»
Цели.
- Вспомнить понятие “перпендикуляр
- Познакомить с понятиями “ медиана, биссектриса и высота треугольника”.
- Научить распознавать в треугольнике медиану, биссектрису и высоту и применять эти понятия при решении задач.
- Сформировать умение строить медиану, биссектрису и высоту.
- Воспитывать у учащихся потребность к обоснованию своих высказываний.
- Развивать эстетические навыки: красоту, точность и аккуратность построения.
- Развивать интеллектуальные навыки: сравнение, классификация, анализ.
- Развивать коммуникативные навыки.
- Воспитывать диалоговую культуру.
- Воспитывать любовь к предмету.
Оборудование урока: экран, проектор, ноутбук, презентация, чертежные инструменты, раздаточный материал.
План урока.
- Организационный момент.
- Геометрический марафон.
- Изучение нового материала.
- Закрепление полученных знаний.
- Контроль усвоения учащимися нового материала.
- Итог урока. Задание на дом.
Ход урока
I. Организационный момент
Проверить готовность к уроку.
Просмотреть домашнюю работу.
Подписать число в тетрадях.
II. Проверка изученного ранее материала
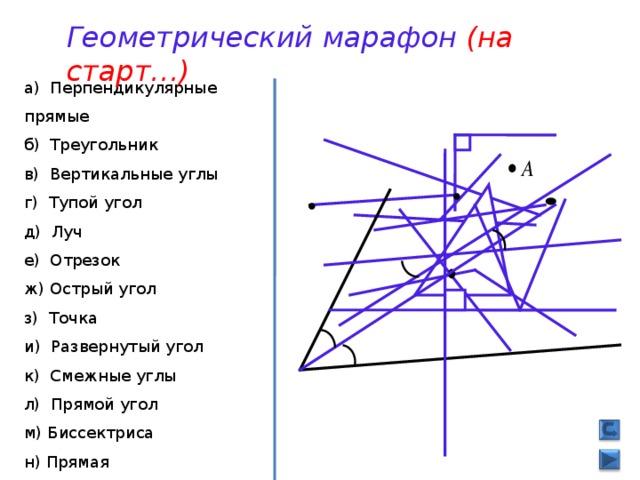
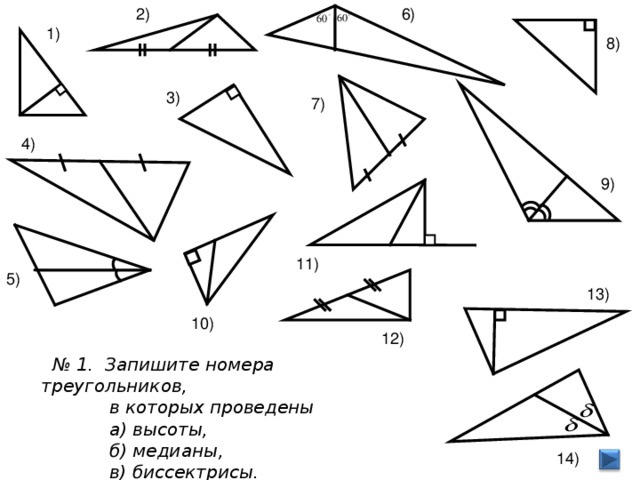
1.сейчас поведём с вами Геометрический марафон. Открыть слайд №1.
Вам необходимо сопоставить фигуру, появляющуюся на экране, с её названием и записать соответствующую букву в клетку листа.
- Взаимопроверка (слайд №2).
- Посмотрите, пожалуйста, какая геометрическая фигура изображена на этом весёлом рисунке? Слайд3 . (Треугольник).
- А что называется треугольником? (Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).
- Сколько вершин у треугольника?
- Сколько у него сторон?
- Какие виды треугольника вы знаете? (прямоугольный, равнобедренный, равносторонний). Дайте им определение.
- Какие треугольники называются равными?
- Назовите 1 свойство равенства треугольников?
- Назовите 2 свойство равенства треугольников?
- Напомните теорему равнобедренного треугольника.
- Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? {Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто – Рико и полуостровом Флорида}.
- А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.
Тема урока: «Высота, биссектриса и медиана треугольника» слайд 4
III. Изучение нового материала
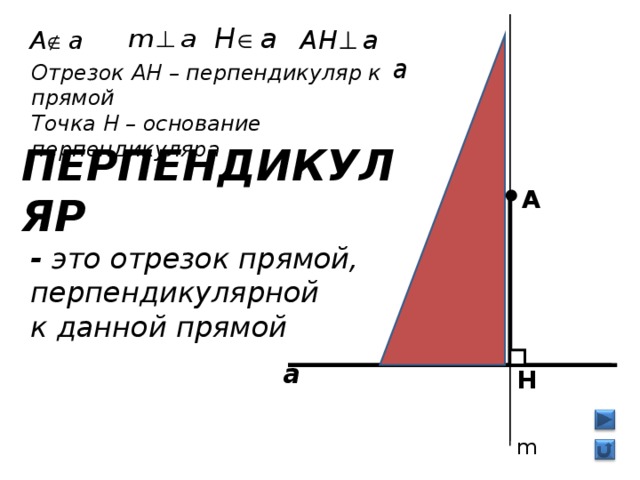
- Введение понятия перпендикуляра (слайд 5 ).
Вспомнить, что означает запись:
Учитель дает задание классу (одновременно идет иллюстрация слайда).
В тетрадях построить прямую а и точку А, не лежащую на этой прямой.
Построить прямую т, проходящую через точку А, и перпендикулярную прямой а.
Построить отрезок АН (та = Н) – перпендикуляр.
Попытайтесь сформулировать определение перпендикуляра и ответить на вопрос “Сколько перпендикуляров можно провести из данной точки А к данной прямой а?”
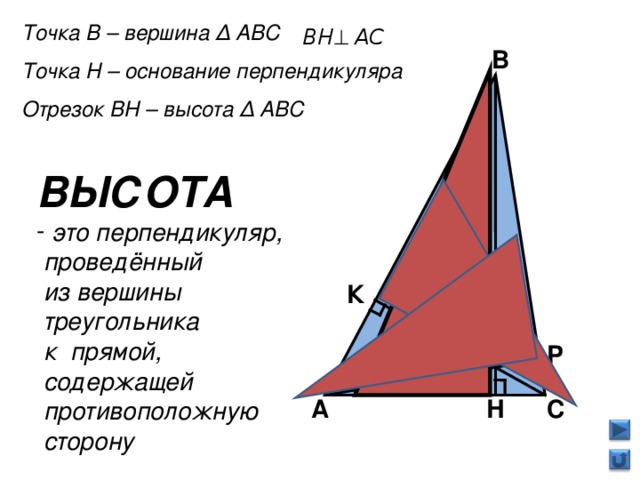
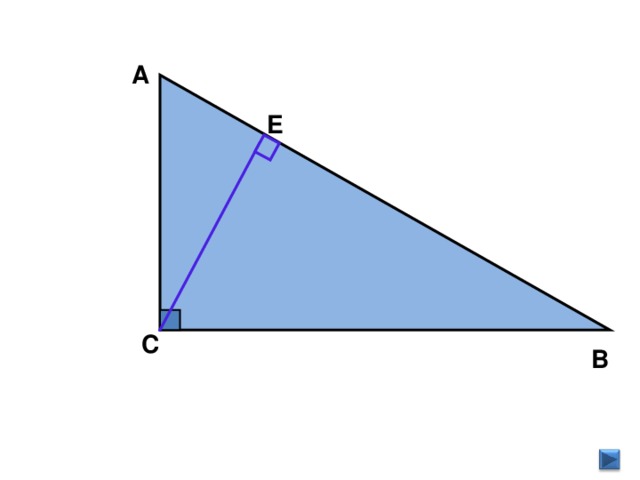
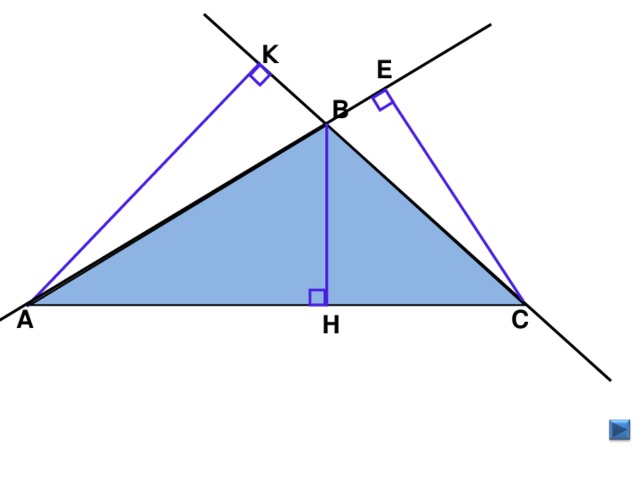
2. Введение понятия высоты треугольника (слайд №6).
а) Учитель показывает построение перпендикуляра из вершины. В на прямую, содержащую сторону АС; говорит, что отрезок ВК называют высотой треугольника АВС
“Сколько высот можно построить в треугольнике?”
Ребята дайте определение высоты треугольника.
Затем открывает формулировку на слайде.
Чтобы легче запомнить, что такое высота, посмотрите на шуточное определение (Слайд 7)
Б) Начертите остроугольный треугольник , постройте высоты. 1 ученик у доски выполняет задание.
В) слайд 8 - какой треугольник здесь изображён? Как провести высоту из прямого угла? Как провести высоты из вершин острых углов треугольника?
г) Перед вами тупоугольный треугольник – постройте высоты в тупоугольном треугольнике. (Здесь возникает проблемная ситуация: как провести высоту из вершины острого угла треугольника.)
Показать построение (слайд №9).
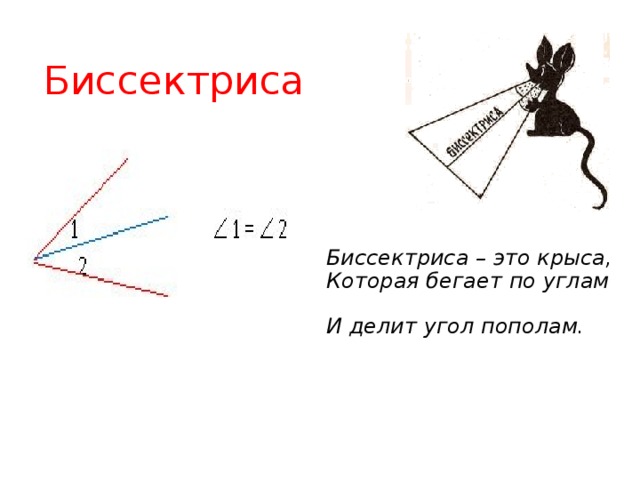
3. Определение биссектрисы угла
Жил-был один ученик. Начав изучать геометрию, он многое не понимал, много делал ошибок. Пытался изучать самостоятельно, думая как же понять эту науку. Часто, стали ночью в его снах приходить геометрические фигуры. Они разговаривали с ним, рассказывали о себе, о том, зачем и для чего они нужны. Вот один из таких снов мы сейчас увидим.
Жила была Медиана треугольника. Разговорилась как-то она с Биссектрисой угла.
М. – Слушай Биссектриса угла, давай познакомимся поближе. Расскажи мне о себе. Кто ты такая, как ты живешь? А я тебе поведаю про себя. Будет на сердце легче. А то люди иногда такое про нас наговаривают, что и сказать стыдно. Их невежество иногда меня в тупик. Как им разъяснить их заблуждения?
Б. – Хорошо добрая Медиана, расскажу. Я тоже этого хотела. Словно прочитала мои мысли. Ну, слушай. Я – Биссектриса угла. И этим многое сказано. Без угла меня нет. Ну, как грома без молнии, как прямой без точки, угла без лучей. Только назовешь, а тебе в ответ: “А где же твой угол?”. Это во-первых. Во-вторых – я луч.
М. – Прости, моя геометрическая фигура, но ведь и стороны угла тоже лучи. Чем же ты от них отличаешься? – спросила Медиана.
Б. – У меня есть сходство с ними уже потому, что я тоже луч. И исхожу я из той же точки что и они. Эту точку называют вершиной угла. Но я отличаюсь от них. Хотя бы тем, что прохожу между сторонами угла. Понимаешь, между! Иногда люди забывают про это и путают меня со всякими другими лучами, тоже исходящими из вершины угла. Даже если они не проходят между его сторонами.
М. – Да, извини, что перебиваю, но между сторонами не ты одна проходишь?
Б. – Да что ты, конечно нет. А вот угол пополам делю я одна. Больше из лучей никто не делит угол пополам.
М. – Теперь я вижу, что фигура ты значительная. Ты и луч, ты и исходишь из вершины угла, да еще и проходишь между его сторонами и делишь свой угол пополам. Ты обладаешь важными свойствами, тебя нельзя не уважать,
Б. – Спасибо за добрые слова.
Слайд10 В. Шуточное определение биссектрисы вы слышали уже не раз.
М. – Это все понятно. Но, скажи, уважаемая Биссектриса угла, как ты связана с треугольником?
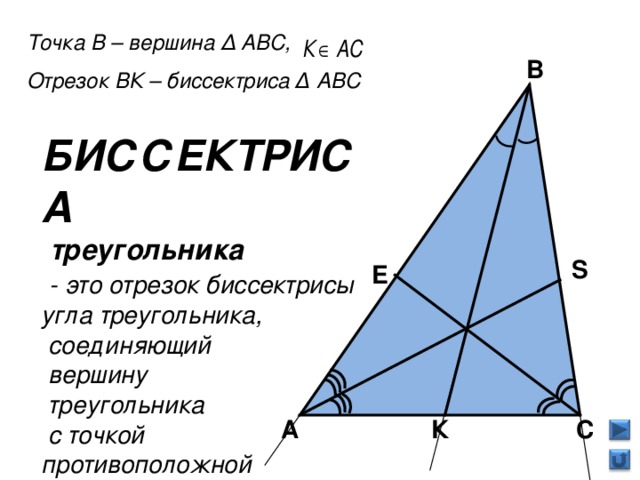
Б. – Конечно расскажу. Имеется не только биссектриса угла, но и биссектриса треугольника. Ты ведь знаешь, что треугольник не то, что угол, он является фигурой ограниченной. Ну и биссектриса у него тоже фигура ограниченная. Она является отрезком и составляет мою часть. А потому Медиана, когда ты совпадаешь с биссектрисой треугольника , то тоже оказываешься моей частью. Вот и выходит, что мы с тобой связаны
М. – Слыхала, Биссектриса угла, что если вас трое и вы становитесь биссектрисами углов треугольника, то у вас есть единственная общая точка. Правда ли это?
Б. – Правда, правда. Биссектрисы углов треугольника пересекаются в одной точке. Почему?
В обратимся к следующему слайду. Начертите треугольник. Проведите биссектрису ВК. Попробуем дать определение биссектрисы. Сколько биссектрис имеет треугольник? Построите ещё 2 биссектрисы.
Построение биссектрис и соответствующая запись.
4. Введение понятия медианы
М. – Спасибо тебе, биссектриса угла, за такой терпеливый и содержательный рассказ о себе. Право, обо мне ты услышишь мало занимательного. Жизнь моя обычна. Но все-таки слушай.
Послушаем и мы о новой для нас фигуре – Медиане.
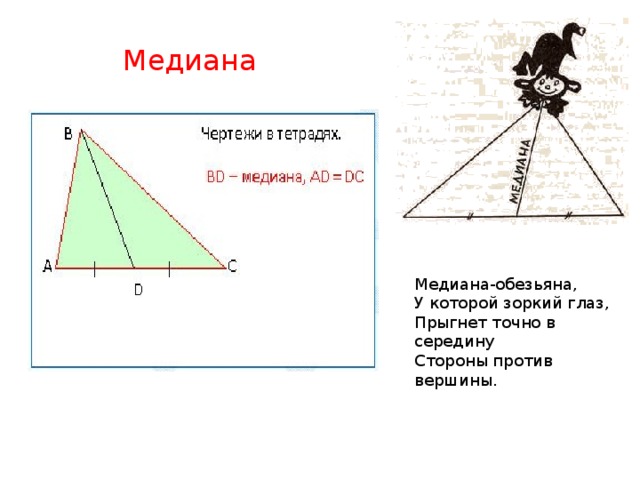
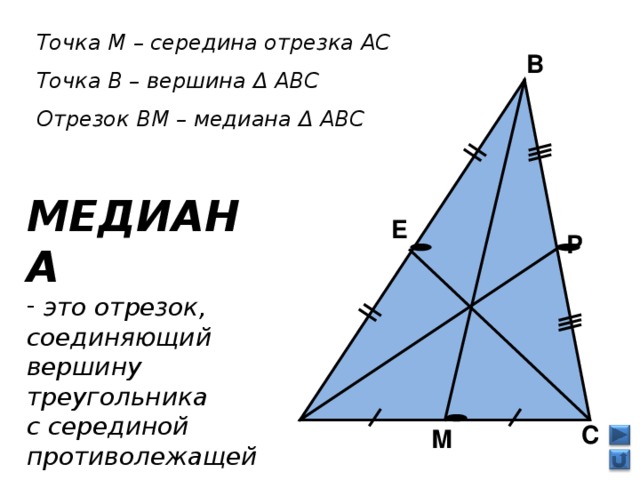
М. – Прежде всего, я – отрезок! Только не любой. А такой, один конец которого совпадает с вершиной треугольника, а другой является серединой противоположной стороны. Слайд 12
Я долго думала, почему это люди обратили на меня внимание, что я за важная птица, чтобы имя мне дать, да еще такое симпатичное: МЕДИАНА! Мало ли отрезков с концами в вершине треугольника да на противоположной стороне? А вот выделили меня вместе с биссектрисой и высотой треугольника! Ну, их, конечно, удостоили специальных названий – по заслугам: одну – за равенство углов, другую – за прямой угол. А меня, что же, выходит за середину стороны? Может и так. Но, думаю, не только за это.
Б. – А за что же еще? Расскажи!
В. немного попозже расскажешь, а сейчас мы с ребятами построим тебя в своих тетрадях и выведем формулировку медианы. Итак начертили треугольник. (слайд 13) – Сколько медиан можно построить в треугольнике?
Попросить одного из учащихся прокомментировать построение медианы.
и соответствующая запись в тетрадях
В. Слушаем тебя медиана.
М. – Ой, да даже не знаю. Рассказывать ли об этом. Дело в том, что сейчас я на время из геометрии выйду в физику. Ты ведь кое-что знаешь о физике?
Б. – Да, конечно кое-что знаю. Мною иногда в физике пользуются. В другой раз я готова даже рассказать об этом.
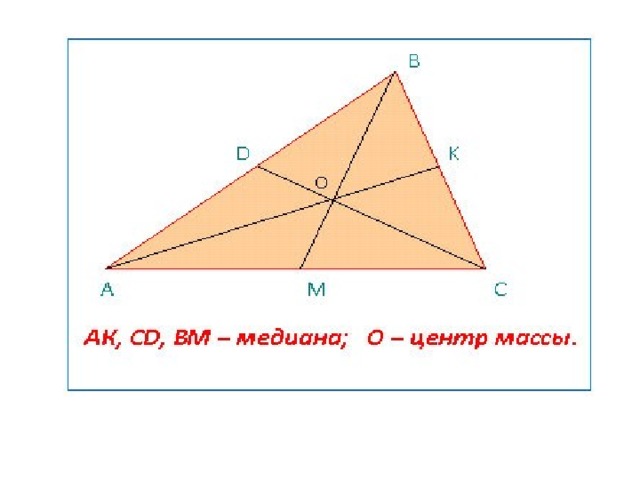
М. – Ну, тогда слушай. Сидим мы как-то вечерком. Мы – это три медианы одного треугольника. Вдруг слышим чей-то бас: “Уважаемые мои медианы, позвольте с вами познакомиться. Я тесно связан с вами тремя”. “Кто ты такой? – спрашиваем. – Как тебя зовут?” А он: “Я являюсь точкой вашего пересечения, но этого мало. – Я ЦЕНТР масс вашего треугольника”. Отвечаем ему: “Мы из геометрии, а ты из физики. Что общего между вами? Объясни”. Но он нам ничего не поведал.
В. О центре массы треугольника вы узнаете на уроке физики. А сейчас просто запомните. Что точка пересечения медиан треугольника является центром массы треугольника. (слайд № 14).
5) Рефлексия определений (понятий).
а) Назвать элемент и дать его определение (слайд №15).
б) Проверочная работа (слайд №16 и №17).
IV. Закрепление полученных знаний. (Решение задач)
Дидактические материалы №1, 3,4
V. Контроль усвоения учащимися нового материала.
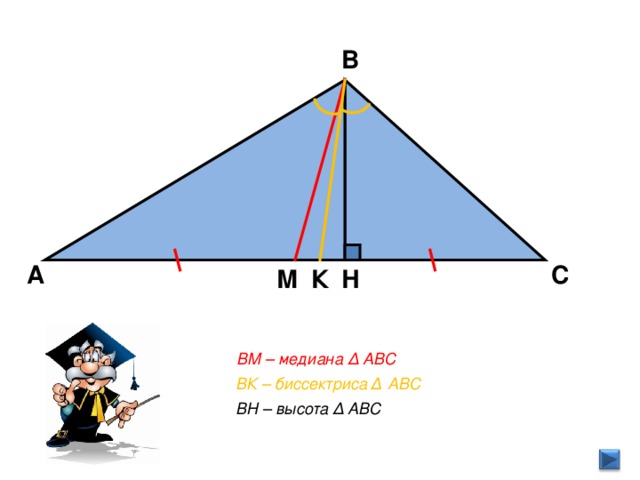
- Работа в парах. На каждой парте лежат три треугольника, разносторонние, разных цветов. На одном из них изображены три медианы, на другом – высоты, на третьем – биссектрисы.
- Покажите треугольник с изображением высот. (Фиолетовые и красные).
- Поднимите треугольник, на котором изображены медианы. (Синие, жёлтые и оранжевые).
- Покажите треугольник с изображением биссектрис. (Зелёные, чёрные).
- Выполним тестовые задания.
1. Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур.
а) Отрезок, соединяющий вершину треугольника с серединой ______________, называется ___________ треугольника.
(Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника).
б) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом _____________.
(Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом единственный).
2. Верны ли следующие утверждения?
а) В любом треугольнике можно провести три медианы. (Да).
б) Точка пересечения высот любого треугольника лежит внутри треугольника. (Не всегда).
в) Все биссектрисы треугольника пересекаются в одной точке. (Да).
V. Итог урока.
Задание на дом: п 25, №19



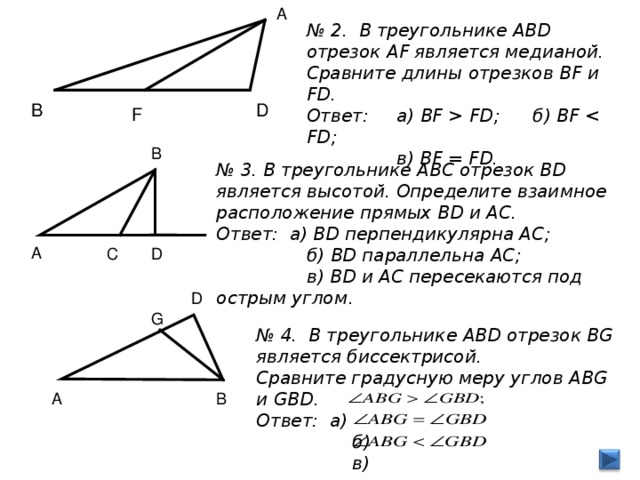 FD ; б) BF FD ; в) BF = FD . D В F В № 3. В треугольнике AB С отрезок BD является высотой. Определите взаимное расположение прямых BD и АС. Ответ: а) BD перпендикулярна АС; б) BD параллельна АС; в) BD и АС пересекаются под острым углом . A D C D G № 4. В треугольнике ABD отрезок BG является биссектрисой. Сравните градусную меру углов ABG и GBD . Ответ: а) б) в) A В" width="640"
FD ; б) BF FD ; в) BF = FD . D В F В № 3. В треугольнике AB С отрезок BD является высотой. Определите взаимное расположение прямых BD и АС. Ответ: а) BD перпендикулярна АС; б) BD параллельна АС; в) BD и АС пересекаются под острым углом . A D C D G № 4. В треугольнике ABD отрезок BG является биссектрисой. Сравните градусную меру углов ABG и GBD . Ответ: а) б) в) A В" width="640"




















