| I. Организационный. (Психологический настрой).
II. Актуализация знаний
III. Постановка проблемы
IV. Открытие «нового» знания
V. Первичное закрепление
Работа в рабочих тетрадях
VI. Самостоятельная работа
VII. .Повторение
VIII. Итог урока
| Здравствуйте, ребята! На прошлом уроке мы с вами закончили изучать очень важные и интересные темы: «теорема Пифагора» и подобие треугольников, прорешали много практических задач. Сегодня мы проведем небольшое исследование. Давайте делиться своими идеями и не бойтесь ошибиться, ведь любая ваша мысль может дать нам новое направление поиска. И все свои достижения мы будем отмечать в оценочных листах. Как в них работать вы знаете.
Сейчас я предлагаю вам решить первую задачу на карточках.
О каком треугольнике идет речь в задаче?
Какой треугольник называется прямоугольным?
Как называются стороны прямоугольного треугольника?
Какие соотношения между сторонами и углами прямоугольного треугольника вы знаете?
- Теперь самостоятельно решите вторую задачу на карточках.
- Смогли ли вы решит задачу?
- Где у вас возникли затруднения?
- Как вы думаете, почему вы не справились с задачей?
Верно. Откроем тетради, запишем число, классная работа и тему урока «Соотношения между сторонами и углами прямоугольного треугольника»
Постройте прямоугольный треугольник
Назовите гипотенузу.
Назовите катет, прилежащий углу А, прилежащий углу В и противолежащий углу А и углу В.
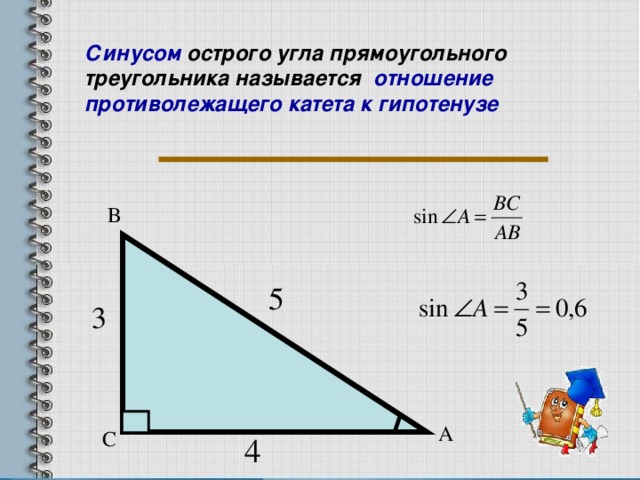
Дается определение синуса острого угла прямоугольного треугольника 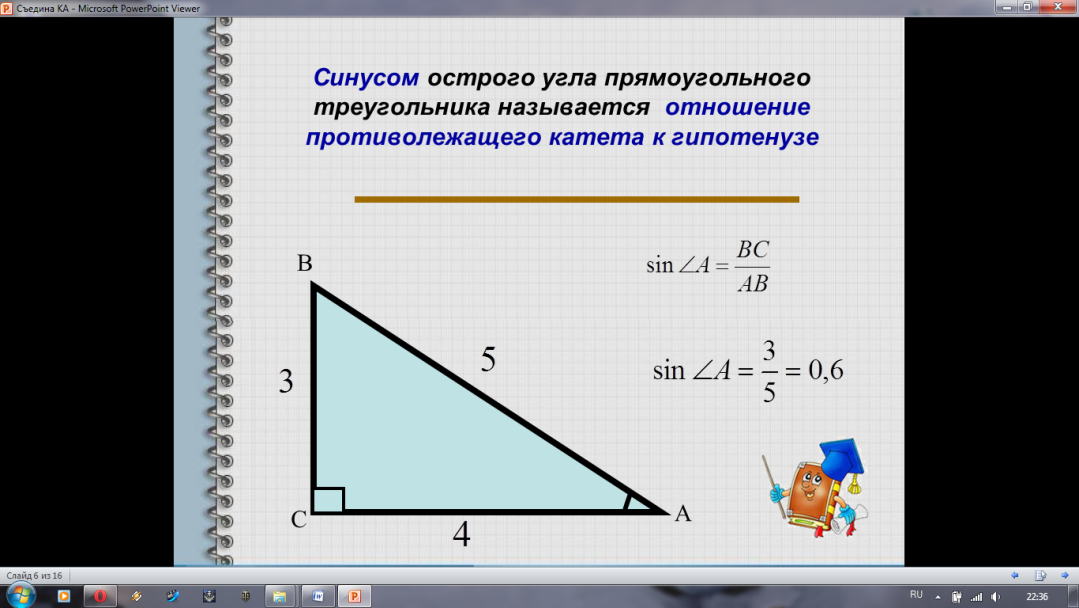
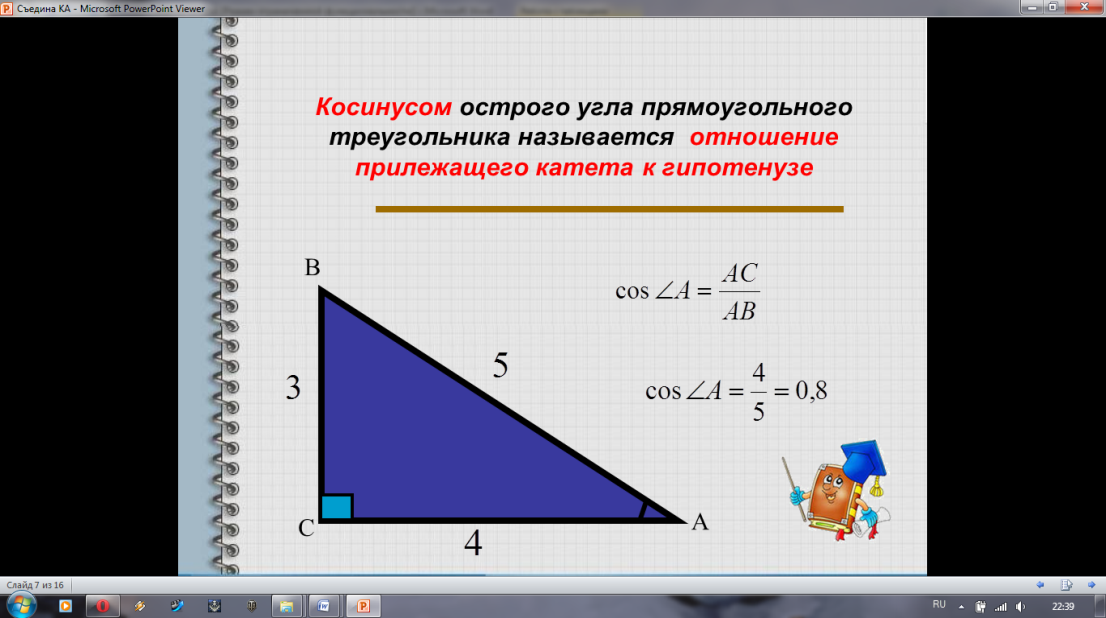
Дается определение косинуса острого угла прямоугольного треугольника
Дается определение тангенса острого угла прямоугольного треугольника 
Эти правила позволяют, зная одну из сторон прям треуг и острый угол, находить две другие стороны; зная две стороны находить острые углы.
Решение задачи из рабочей тетради (геометрия, рабочая тетрадь 8 класс, автор Л.С. Атанасян и др) стр. 33 № 71
Теперь вернемся к нашей второй задачи на карточках.
Хватит ли сейчас нам знаний решить ее?
Нам известны катет ВС и гипотенуза АВ, что мы сможем найти?
Как определить градусную меру угла А, зная его синус?
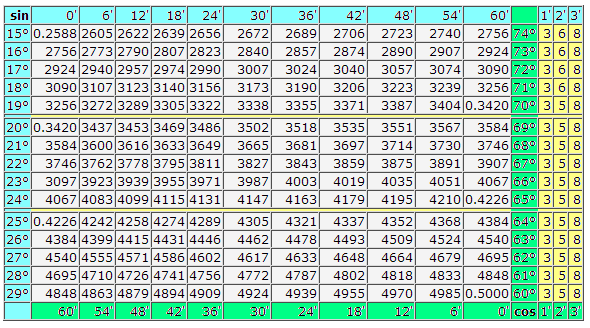
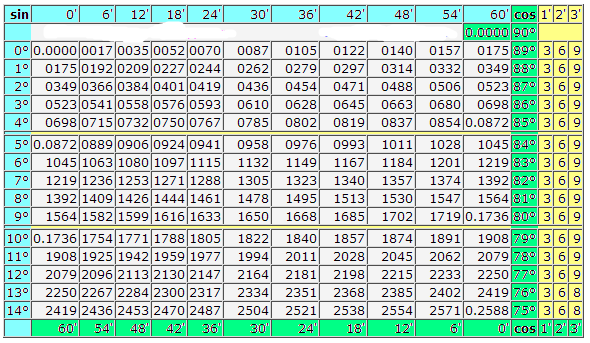
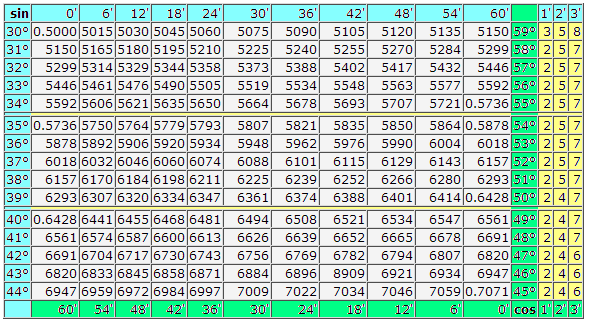
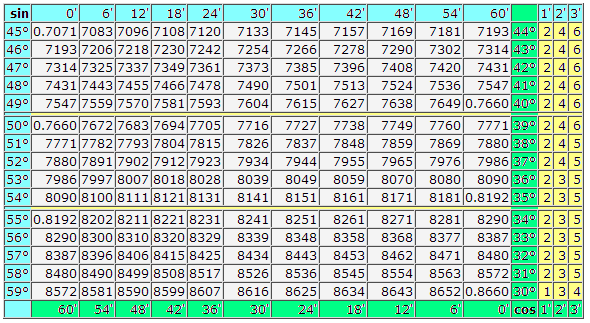
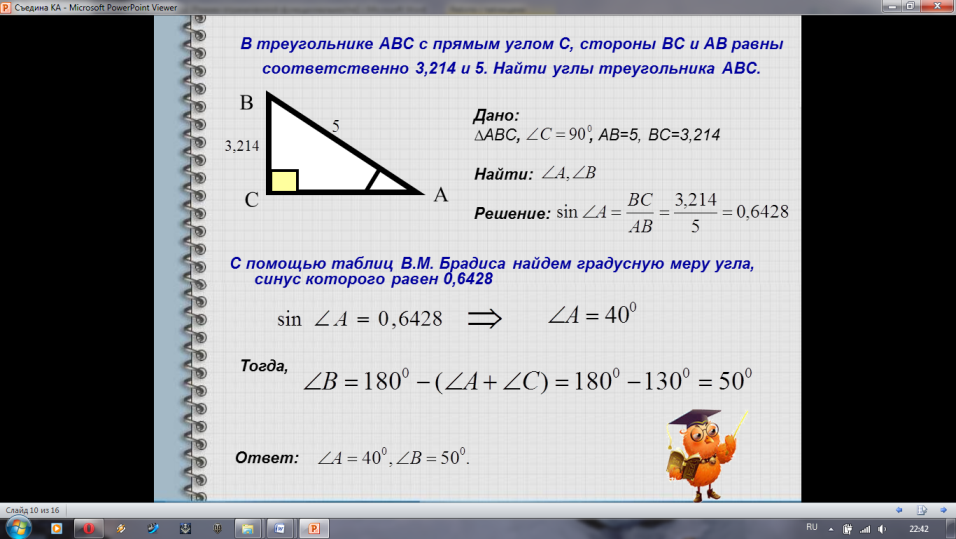
В этом нам помогут «Четырехзначные таблицы Брадиса» для синусов и косинусов.
Рассказ учителя Заслуга Брадиса состояла в том, что он придумал способ, позволяющий до минимума сократить утомительные расчеты. Кропотливых расчетов Брадису предстояло проделать много, их он представил в виде таблиц. Эти таблицы стали советским бестселлером. С 1930-х годов их издавали ежегодно в течение 30 лет. Эту книжку читали миллионы. Школьники, студенты, инженеры – таблицы Брадиса были у всех. Однако миллионером он не стал, но прожил жизнь вполне благополучно. Сегодня мы научимся находить значения синусов и косинусов целых углов.
Зная, что синус угла А равен 0,6428, определите градусную меру этого угла.
Решить задачу № 591 (б), стр. 159 по учебнику самостоятельно.
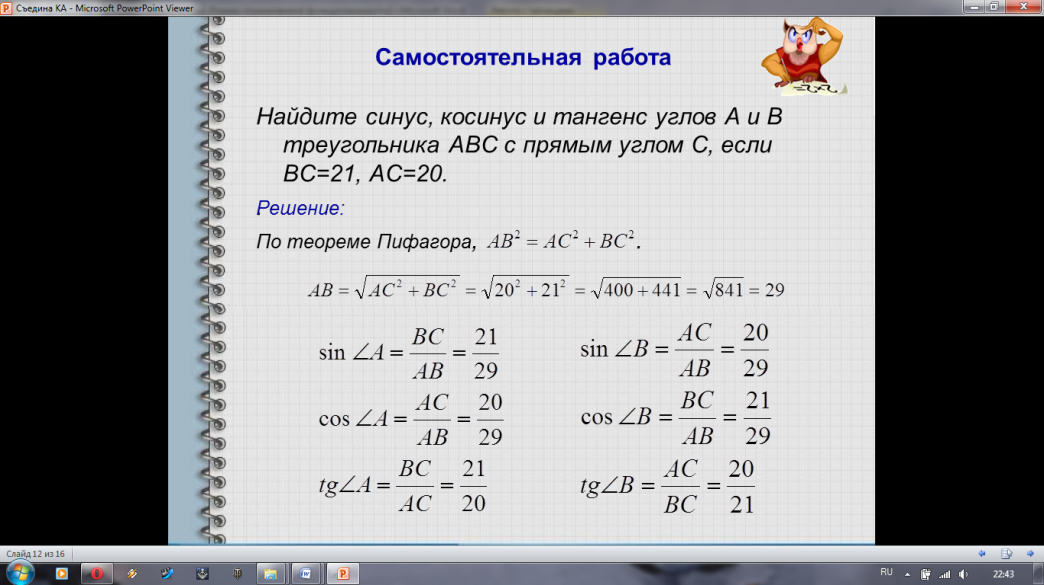
По готовому образцу идет проверка задачи.
С какими понятиями мы с вами сегодня познакомились?
Верно. Мы с вами узнали о новых соотношениях между сторонами и углами прямоугольного треугольника.
А зачем скажите вы? Мы знаем, что можно с помощью линейки измерить длину отрезка, транспортиром измерить угол. Однако не всякую величину можно измерить непосредственно. Например, как измерить высоту солнца над горизонтом? Как определить длину моста, который нужно построить через реку? Каково расстояние от маяка до корабля?” Чтобы ответить на все эти и многие другие вопросы, нам нужны новые знания. Предлагаю вам решить практическую задачу.

А теперь подведем итоги нашего исследования
В оценочных листах подведите итог и передайте на первую парту.
Рефлексия: - С какими понятиями мы с вами сегодня познакомились?
-Что вам больше всего понравилось?
Что удивило?
Домашнее задание: пар. 4, пункт 66, вопросы 15-17, стр 154, № 591(а,в,г), раб тетрадь №72. | Включаются во взаимодействие с одноклассниками и с учителем.
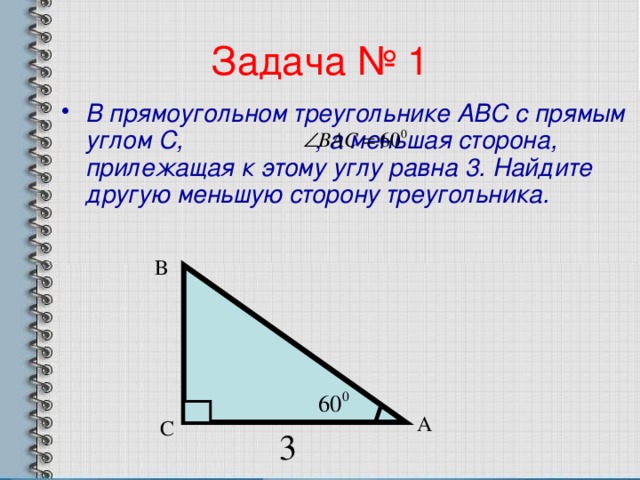
Читают задачу. «В прямоугольном треугольнике АВС с прямым углом С, угол ВАС равен 60°, а меньшая сторона, прилежащая к этому углу равна 3. Найдите другую меньшую сторону треугольника»
В задаче говорится про прямоугольный треугольник.
Треугольник называется прямоугольным, если один из его углов равен 90º.
У прямоугольного треугольника большая сторона называется гипотенузой, а две другие - катетами.
1.В прямоугольном треугольнике напротив угла в 30º, лежит катет, равный половине гипотенузы. 2. В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. 3. В треугольнике против большей стороны лежит больший угол.
Заносят результаты опроса в оценочные листы
Один ученик решает задачу у доски с комментарием.
1.Сумма углов в треугольнике 180º, следовательно, 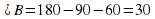 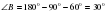 . . 2.В прямоугольном треугольнике, против угла в 30°, лежит катет равный половине гипотенузы, след, АВ=6. 3. По теореме Пифагора 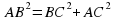 , след. , след. 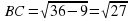 . .
Самостоятельно пробуют решить задачу «В треугольнике АВС с прямым углом С, стороны ВС и АВ соответственно равны 3,214 и 5. Найти углы треугольника АВС»
- Нет!
Идет подробный разбор задачи. (Обычно учащиеся начинают решение с нахождения второго катета по теореме Пифагора, затем наступает затруднение)
Обучающиеся проходят к выводу, что существуют еще и другие зависимости между сторонами и углами прямоугольного треугольника.
Формулировка целей урока.
Строят треугольник В 
С А
Гипотенуза АВ.
В треугольнике АВС углу А прилежит катет АС, углу В – ВС, противолежит углу А катет ВС, противолежит углу В – катет АС.
Записывают определения в тетрадь
Трое учащихся решают задачу с подробным объяснением.
Да!
Зная гипотенузу АВ и катет ВС, можно найти синус угла А. 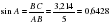
Учащиеся затрудняются ответить на этот вопрос.
Идет объяснение: как найти синус и косинус 35°, 50°. (у каждого ученика на парте лежат таблицы Брадиса)
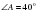
Тогда, 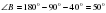
(учащиеся должны самостоятельно решить задачу и проверить с учителем по готовому образцу)
Заносят результаты самостоятельной работы в оценочные листы
Синус, косинус и тангенс острого угла прямоугольного треугольника.
Один ученик выходит к доске для решения практической задачи.
Выставляют итог в оценочных листах
Синус, косинус и тангенс острого угла прямоугольного треугольника.
1.Находить значения синусов, косинусов по таблицам Брадиса. 2.Решать практическую задачу
Знание геометрии позволяет решать много практических задач.
| Включить детей в урок. Настроить максимальное количество детей.
Учащиеся должны воспроизвести в памяти знания необходимые для усвоения нового материала.
Организовать решение проблемной ситуации.
Решение заданий на новое знание с комментированием громкой речью.
Создать условия для самостоятельного решения и нахождения ошибок в работе.
Организовать выполнение заданий, для решения которых, необходимы новые и старые знания.
Организовать анализ деятельности учащихся на уроке
|






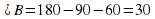
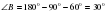 .
.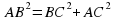 , след.
, след. 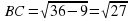 .
.
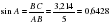
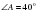
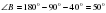
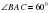 , а меньшая сторона, прилежащая к этому углу равна 3. Найдите другую меньшую сторону треугольника.
, а меньшая сторона, прилежащая к этому углу равна 3. Найдите другую меньшую сторону треугольника.