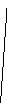ОТКРЫТЫЙ УРОК ПО ГЕОМЕТРИИ
« Применение признаков равенства треугольников к решению задач»
7г класс
Учитель: Гурьянова Валентина Викторовна
Цель урока: научиться применять теоретические знания (признаки равенства треугольников, свойства равнобедренного треугольника) при решении задач.
Задачи урока: 1.Образовательные:актуализировать опорные знания; выявить степень усвоения материала;
2.Воспитательные: - воспитывать аккуратность;- формирование отношений взаимной ответственности и зависимости в группах.
3.Развивающие: постановка и развитие правильной математической речи; расширение кругозора учащихся; развивать умения видеть
математические понятия в окружающем нас мире; - развивать логическое мышление, применять дедуктивный метод
при решении задач.
Тип урока: комбинированный с применением групповой работы и с элементами исследования.
Оборудование урока:
-
Раздаточный материал: карточка с индивидуальным заданием; карточки-задания для групповой работы и домашней работы; модели треугольников, четырехугольников и пятиугольников для оценки работы учащихся в группах; квадраты из бумаги.
-
Презентация .
-
Тест с практическими и теоретическими заданиями для итогового контроля.
План урока.
1. Организационный момент.
2.Мотивация изучения темы. Постановка проблемы.
3. Актуализация опорных знаний.
4.Устные упражнения. Решение задач по готовым чертежам.
5.Физкультминутка. Упражнения для глаз.
6. Работа в парах. Индивидуальная работа у доски.
7.Практическое применение знаний.
8. Постановка домашнего задания.
9. Итог урока. Тест.
10. Рефлексия.
Ход урока.
1. Организационный момент. (1 мин.)
-
-
Проверка готовности учащихся к уроку.
-
Здравствуйте, ребята! Садитесь. Сели все прямо, посмотрели на меня, улыбнулись друг другу! Начинаем урок!
Сообщение темы и целей урока.
2.Мотивация изучения темы. Постановка проблемы.
1). В нашей местности много озер. Ширину не каждого озера мы знаем. Пусть нам нужно определить ширину озера, изображенного на рисунке. Как вы думаете, как это можно сделать?
Решение.
Чтобы измерить ширину озера (расстояние АВ на рисунке) на местности потребуется 4 колышка и веревка. Отмечают точки А и В,далее провешивают на местности прямую ВD,на ней выбирают точку С, из которой видна точка А С под прямым углом, и откладывают отрезок СD, равный отрезку ВС . Какое расстояние на местности надо измерить, чтобы узнать ширину озера?
( Для этого надо измерить длину отрезка АD, так как треугольник АВD = треугольнику АСВ по двум сторонам и углу между ними, значит, АВ = АD).
2). Какие знания нам нужны для решения этой задачи?
3. Актуализация опорных знаний.
1). Определение треугольника. Первое упоминание о треугольнике и его свойствах мы находим в египетских папирусах которым более 4000 лет.
2) Виды треугольников в зависимости от величины углов.
3) Виды треугольников в зависимости от длин сторон.
4). Определение равнобедренного треугольника.
5) Определение равностороннего треугольника.
6) Элементы треугольника ( медиана, биссектриса и высота)
7). Как сравнить два треугольника?
8) Определение равных треугольников.
9) Формулировки признаков равенства двух треугольников?
УЧИТЕЛЬ: Замечательная и таинственная геометрическая фигура и самая популярная в школьной программе по геометрии- это треугольник. Может, вы думаете, что треугольники поселились только на страницах учебника геометрии и больше их нигде не увидеть? Наверное только школьники старательно изучают и рисуют треугольники? В этом вас постарается разубедить ваш одноклассник. ( выступление ).
4.Устные упражнения. Решение задач по готовым чертежам.
№1 (устно). По готовому чертежу докажите равенство треугольников.
№2 (устно). №3 (устно).№4(устно)
4) Назовите необходимое условие для того, чтобы треугольники АВС и МРО были равны а) по 1 признаку б) по 2 признаку
5) На рисунке МР=МТ, РК=ТК. Какие точки доcтаточно соединить, чтобы получились равные треугольники?
5.Физкультминутка. Упражнения для глаз.
6. Работа в парах. Индивидуальная работа у доски.
1) Двое учащихся выполняют задания у доски
Задача 1.
Задача 2.
2).Работа в парах
1 группа
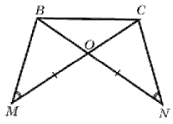
Дано: МО=ОN, АМ=DN, АВ=СD, <ВМО=<СNО
Доказать: ?АВМ=?DСN
-
Равенство каких треугольников мы можем доказать?
-
Из равенства треугольников ?МВО=?NСО какие элементы мы возьмем?
-
Теперь мы сможем доказать равенство ?АВМ=?DСN?
Доказательство:
1) ?МВО=?NСО по стороне и двум прилежащим к ней углам. В равных треугольниках соответственные стороны равны, значит МВ=NС
2) ?АВМ=?DСN по трем сторонам.
2 группа
Дано: МО=ОN, угол М равен углу N
Доказать: ?ВОС - равнобедренный
-
Какой треугольник называется равнобедренным?
-
Как доказать равенство сторон ВО и ОС?
-
Правильно, сначала нужно доказать равенство ?МВО=?NСО.
Доказательство:
?МВО=?NСО по стороне и двум прилежащим к ней углам. В равных треугольниках соответственные стороны равны, значит ВО=ОС, значит ?ВОС - равнобедренный, т.к. у него две стороны равны.
3 группа.
Дано: AK=DN, BK=BN
Доказать: ?ABK=?DBN
7.Практическое применение знаний.
«В жизни мы сталкиваемся с множеством практических задач, решить которые нам помогает математика науке»
Задача: Мама купила 1 метр ткани шириной 1 метр на платок двум своим дочерям. Разделите этот кусок ткани на две равные части, сделайте так, чтобы дочери не поругались.( платки были равными) и докажите правильность своих действий.
Решив соответствующую геометрическую задачу, вы снова возвращаетесь к практической стороне исходной задачи, и даете ответ на поставленный в ней вопрос. Именно так часто приходится поступать при решении практических задач на производстве, в технике, в науке.
Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).
Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно. Предполагают, что его способ состоял в следующем: пусть A – точка берега, B – корабль на море. Для определения расстояния AB восстанавливают на берегу перпендикуляр произвольной длины AC AB; в противоположном направлении восстанавливают CE AC так, чтобы точки D (середина AC), B и E находились на одной прямой. Тогда CE будет равна искомому расстоянию AB. Доказательство основывается на втором признаке равенства треугольников (DC = DA; С = A; EDС = BDA как вертикальные).
У доски проговаривается путь решения этой задачи. Учитель задает лишь наводящие вопросы.
-
С помощью какого инструмента можно построить на местности АС перпендикулярно АВ? (экер, теодолит)
-
С помощью какого инструмента на местности можно измерить угол АВС? (астролябия).
-
8. Домашнее задание
Итог урока. Тест
Рефлексия
При изучении признаков равенства треугольников …
Я узнал(а), что…
Я узнал(а), как…
Мне стало понятно…
На следующих уроках по геометрии…
Мы изучили признаки равенства треугольников для того, чтобы…
-
Самооценка
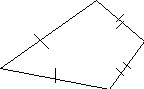
У вас на столах геометрические фигуры: пятиугольник, четырёхугольник, треугольник. Поднятием одной из фигур оцените свою деятельность на уроке.
Подпишите на фигуре свою фамилию и сдайте их мне.




 А
А В Чтобы измерить ширину озера (расстояние АВ
В Чтобы измерить ширину озера (расстояние АВ веревка. Отмечают точки А и В,
веревка. Отмечают точки А и В,  прямым углом, и откладывают отрезок СD,
прямым углом, и откладывают отрезок СD, 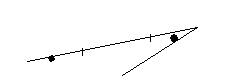


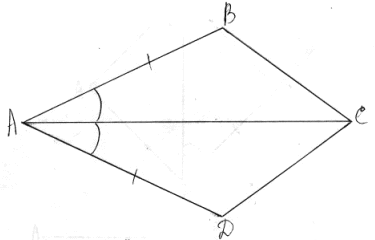 РИС.1
РИС.1 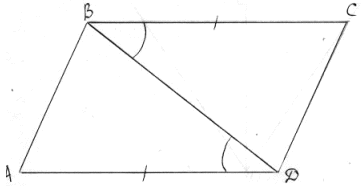 Рис.2
Рис.2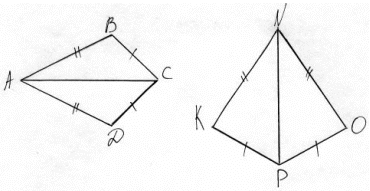


 2 группа
2 группа