Конспект открытого урока по теме «Первый признак равенства треугольников»
Тип урока - Объяснение нового материала
Цель урока: Формирование понятия первого признака равенства иреугольников
Задачи урока:
- Постановка проблемы, будут ли равны треугольники с данными элементами?
- Сформулировать и доказать теорему «Первый признак равенства треугольников».
- Отработать применение теоремы на различных задачах, используя дифференцированный подход.
План урока.
1.Устный опрос теории по теме «Треугольники» в форме «заполнить пропущенные слова»
2.Постановка проблемы.
3.Формулировка и доказательство теоремы (конструктивное построение доказательства теоремы).
4. Решение задачи из учебника, подробная запись решения.
5. Формулировка правила решения задач.
6.Самостоятельное решение задач по готовым чертежам (задание выполняют в виде теста).
1 часть. Доказать равенство треугольников по первому признаку (работают с цветными карандашами).
2 часть. Найти на рисунке треугольники, равные по первому признаку.
3 часть. Доказать, что треугольники равны (задание на «5»).
Ход урока.
1. Вопросы по теме «Треугольники. Признаки равенства треугольников».
- Треугольник – это …, которая состоит из … точек, …. на одной прямой и трех …, попарно соединяющих эти точки.
- Два треугольника называются равными, если их можно наложением ….
- В равных треугольниках против соответственно равных сторон лежат … углы.
И обратно: против соответственно равных … лежат равные ….
4. Точки А, В, С треугольника, изображенного на рисунке называются … треугольника; отрезки АВ, ВС, АС называются … треугольника.
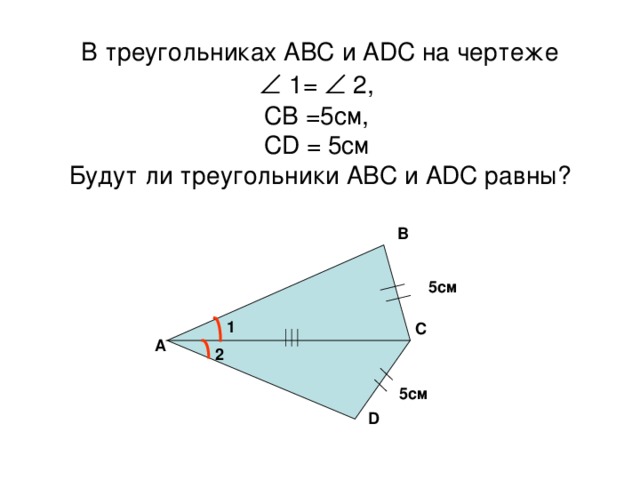
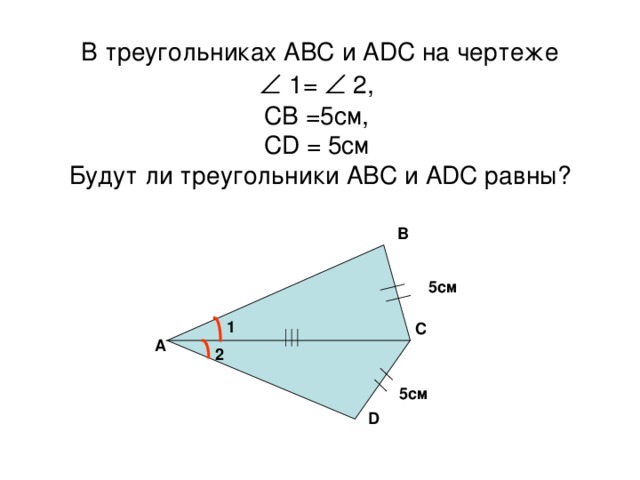
5. В треугольниках АВС и АDС на чертеже 1=2, СВ =5см, СD = 5см. Будут ли треугольники АВС и АDС равны?
2. Постановка проблемы.
Оказывается, что равенство двух треугольников можно установить, не накладывая один треугольник на другой, а сравнивая только некоторые их элементы.
Такая идея очень важна для практики, например для сравнения двух земельных участков, которые конечно нельзя наложить друг на друга.
С этой и многими другими задачами нам поможет разобраться теорема, которую мы сегодня изучаем.
Итак, тема урока «Первый признак равенства треугольников»
Цель урока: сформулировать и доказать теорему и применять ее при решении задач
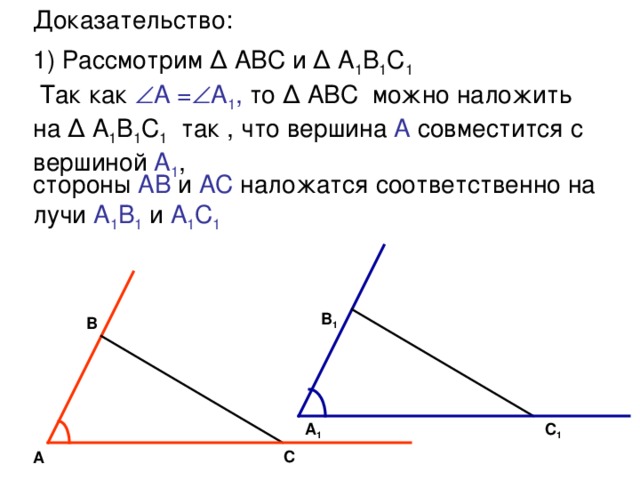
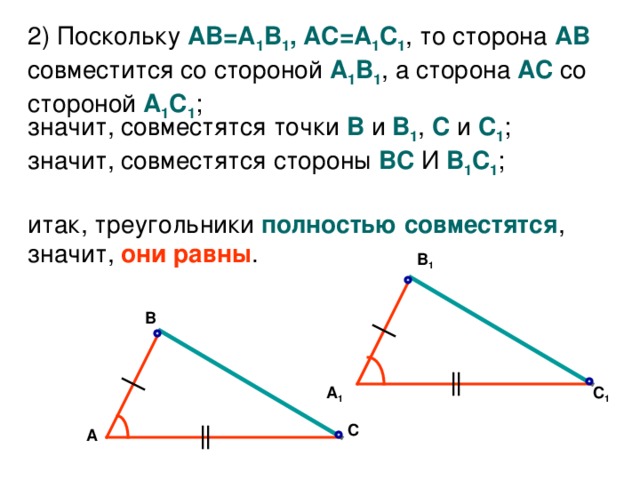
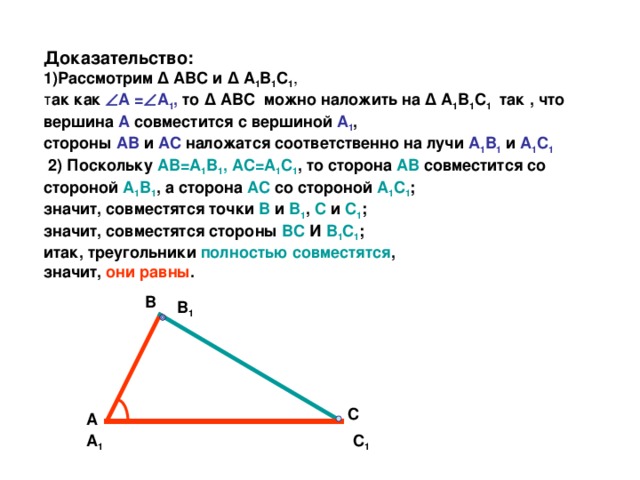
3.Формулировка и доказательство теоремы.
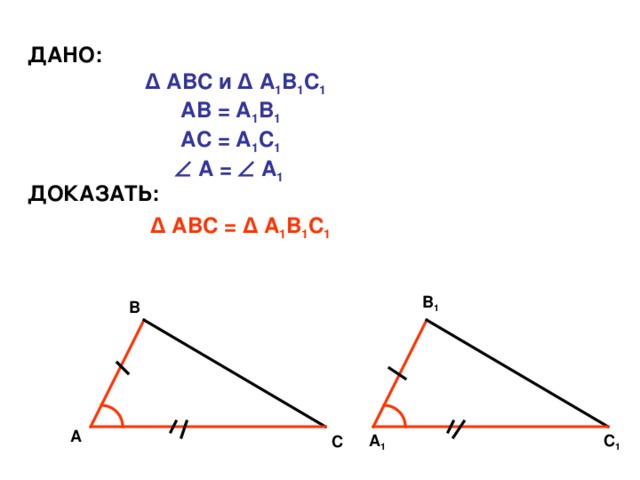
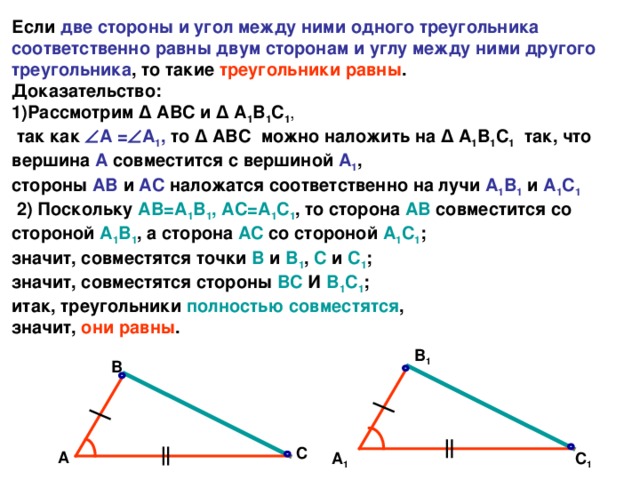
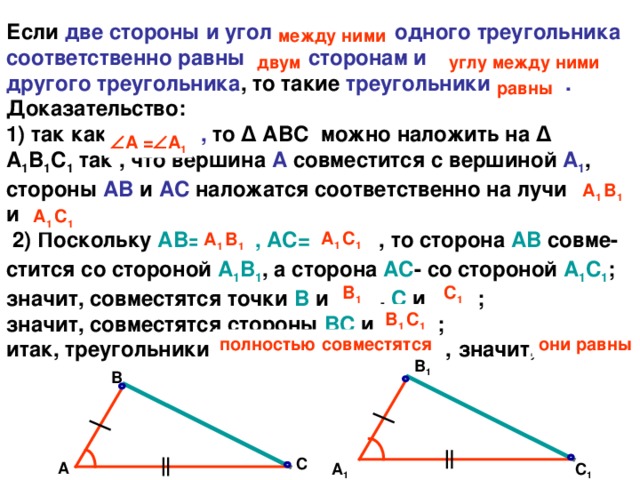
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны?
Использую презентацию
После доказательства теоремы возвращаемся к условию задачи.
В треугольниках АВС и АDС на чертеже
Ð 1= Ð 2,
СВ =5см,
СD = 5см
Будут ли треугольники АВС и АDС равны?
Вначале выслушать тех, кто скажет, что треугольники не равны, проверить, что треугольники не равны с помощью слайда и сделать вывод:
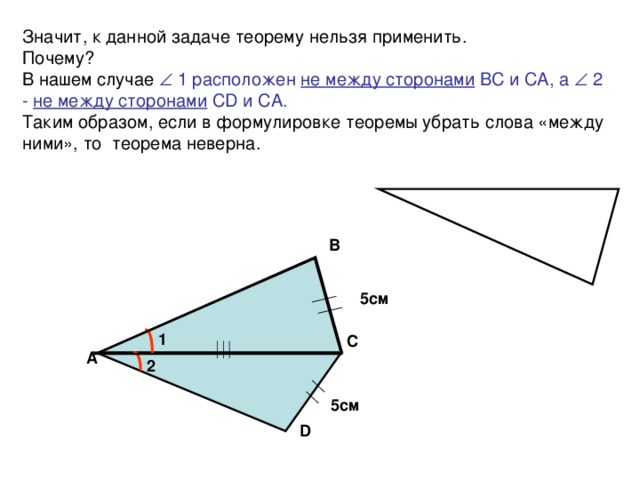
Значит, к данной задаче теорему нельзя применить.
Почему?
В нашем случае Ð 1 расположен не между сторонами ВС и СА, а Ð 2 - не между сторонами СD и СА.
Таким образом, если в формулировке теоремы убрать слова «между ними», то теорема неверна.
4. Решение задачи из учебника, подробная запись решения.
№ 93 Решает группа сильных учащихся.
Дано:
В- сер. АЕ
В-сер. DС
Доказать: ΔАВС=ΔЕВD
Найти углы А и С треугольника АВС, если в треугольнике ВDЕ D=47°, Е =42°.
5.Формулировка правила решения задач.
Правило
Чтобы доказать, что данные треугольники равны по первому признаку, надо:
1) найти у первого треугольника сторону, равную какой-нибудь стороне второго треугольника;
2) среди двух оставшихся сторон первого треугольника найти сторону, равную одной из двух оставшихся сторон второго треугольника;
3) проверить, что угол между выбранными сторонами первого треугольника равен углу между выбранными сторонами второго треугольника.
6. Выполнить тест по готовым чертежам.
7. Подведение итогов и оценка результатов деятельности на уроке.
Тест по теме «Первый признак равенства треугольников»
- Доказать равенство треугольников по первому признаку:
а) б)
- Найти на рисунке треугольники, равные по первому признаку: 3.Доказать равенство треугольников: