Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Конспект урока по теме "Производная"
Урок по теме "Производная" по типу- урок соревновение КВН, проводился в 10 классе ( общеобразовательном). Уровень успеваемости в классе средний. При подготовке к уроку это было учтено. Данный урок последний в серии уроков на тему "Производная". Цели урока: Выяснить степень усвоения учищимися понятия "Производная" и таблицы производных элементарных функций, что значительно помогает при сдачи ЕНТ. На уроке рассматривались задачи на геометрические и механические приложения производной.В конспекте 12 взаимосвязанных этапов, которые проводятся в игровой форме.. Каждый этап оценивается жюри в баллах. За правильный ответ +1, за неверный ответ - 1 балл. В командах по 5 человек, которые болжны быстро ориентироваться в информационном простринстве. На этапе "домашнее задание" учащиеся подготовили проекты по теме "Производная сложной функции". На этапе проверка теоретических знаний учащиеся давали блиц-ответы. В следующем конкурсе "Разминка" на интерактивной доске решалиь устные и письменные примеры на вычисление производной, нахождение промежутков монотонности. В конкурсе "блицтурнир" учащиеся решали задания типа "Что бы это значило?" и "Найди ошибку". Ответы давались на обратной стороне доски. В конкурсе "художников" решались задачи на составление уравнения касательной. В конкурсе "математический футбол" учащися составляли задание по готовым рисунккм. В конкурсе "Юные физики" рассматривался механический смысл производной в решении задач на кинетическую энергию тела. В подведении итогов урока принимали участие члены фюри и капитаны команд. Психологическая атмосфера на уроке была положительная, учащиеся чувствовали себя комфортно, не стеснялись высказывать свои мысли.Цели урок достиг
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«конспект урока по теме "Производная" »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1400 руб.
2330 руб.
1490 руб.
2480 руб.
1900 руб.
3170 руб.
1060 руб.
1760 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


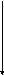 y
y
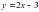
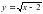
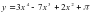
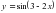
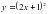
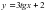

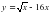
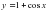
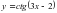
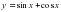
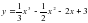
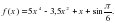
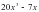 Б)
Б) 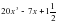 В)
В) 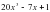
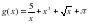 в точке
в точке 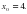
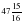 Б) 44 В)
Б) 44 В) 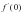 и
и 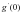 , если
, если 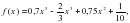
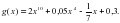
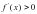 , если
, если 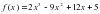 .
.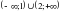 Б)
Б) 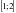 В)
В)