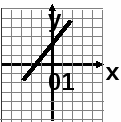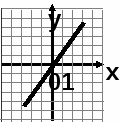Урок математики в 7 классе.
Учебник: Н.Я. Виленкин, В.И. Жохов, А.И. Чесноков «Математика 6»
Тема урока: «Прямая пропорциональность и её график»
Тип урока: объяснение нового материала
Цели:
- Образовательная: познакомить с понятием «прямая пропорциональность»; научить распознавать среди других функций, определять коэффициент к; научить кодировать информацию с помощью схем; сформировать умение строить график функции вида y=kx; показать возможности дальнейшего использования прямой пропорциональности;
- Развивающая: способствовать развитию интеллектуальных навыков: сравнение, классификация, анализ; развитию коммуникативных навыков.
- Воспитательная: воспитывать диалоговую культуру; любовь к предмету.
ХОД УРОКА
1.
Уч: Девизом к сегодняшнему уроку я предлагаю слова математика и педагога Дьёрдь Пойа или Джордж Полиа «Лучший способ изучить что – либо – это открыть самому» (слайд №1)
Уч: Ребята, к изучению какого раздела мы с вами приступили?
Д: Функция.
Уч: Давайте вспомним, какие вопросы мы уже рассматривали.
Д:
- Выяснили, что такое функция.
- Узнали, что такое область определения и область значений функции.
- Узнали, как можно задать функцию.
- Узнали, что называется графиком функции.
- Какая переменная является зависимой, а какая – независимой.
Уч: Верно. А сейчас выполните задание. На столах у вас находятся карточки. Карточка №1. (Слайд №2) дублирует ваши задания. Выполняем задание письменно в тетради. Работа индивидуальная.
Карточка №1.
1. Дана функциональная зависимость s от t, где s – путь в км, пройденный туристом за t ч с постоянной скоростью 5 км/ч
2. Дана функциональная зависимость С от x, где С- стоимость товара в рублях по цене 25 р. за килограмм, х- масса товара в килограммах.
3. Дана функциональная зависимость S от a, где S–площадь квадрата в м ,со стороной a м.
4. Дана функциональная зависимость Р от a, где Р- периметр квадрата в см, a – длина стороны в см.
- а) Каким способом заданы эти 4 функции?
- б) Задайте каждую из этих функций формулой.
- в) Какую из формул вы выделили бы в отдельную группу?
Уч: Давайте проверим, что у вас получилось (слайд №3)
1) S=5t 2) C=25x 3) S=а2 4) P=4a
3) S=а2
Уч: Обратите внимание на формулы функций. Ребята, это примеры функции, которая носит название прямая пропорциональность. А с такой функцией мы с вами встречались?
Д: Да, встречались.
Уч: Мы только не знали, что это прямая пропорциональность. В школьном курсе мы будем изучать различные функции и квадратичные, и логарифмические, и тригонометрические…Но с ними мы познакомимся в старших классах. И чтобы нам отличать прямую пропорциональность от остальных, сегодня тема нашего урока: «Прямая пропорциональность и её график». (слайд №4 с названием темы урока)
Уч: Как вы думаете, какие вопросы, возможно, возникнут при изучении этой темы?
Д:
- Какую функцию называют прямая пропорциональность?
- Какой формулой можно задать?
- Как распознать её среди других объектов?
- Что является графиком прямой пропорциональности?
- Как построить график прямой пропорциональности?
- Какие операции можно выполнять с графиком прямой пропорциональности?
Уч: Верно, ребята. Я, верно, поняла вас, что нам необходимо:
1) Узнать определение
2) Распознавать среди других
3) Уметь строить график
(на доску наклеивается план изучения темы)
2.
Уч: В изучении нового как всегда помогут наши «старые знакомые» - знания. Это мостик от старых знаний к новым.
Сейчас вы будете работать в парах. Возьмите в руки карточку №2, которая лежит на вашем столе. Карточка называется «Проверь себя». Это математическая мозаика, она содержит пять утверждений. Вы должны или закончить утверждение или воспроизвести его начало. Вам даны варианты ответов, среди которых вы должны выбрать нужный. Будьте внимательны (дети под руководством учителя работают с карточками.)
Уч: А теперь проверим, что у вас получилось. Сейчас мы выполним самопроверку, как обычно выставляя «+» за каждое верно выполненное задание.
(дети по парам поочередно читают свои ответы, на экране появляются слайды с верными ответами)
Проверь себя. (слайд №5)
- Функцией называют такую зависимость одной переменной от другой, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной. (слайд №6)
- Все значения, которые принимает независимая переменная, образуют область определения функции. (слайд №7)
- Все значения, которые принимает зависимая переменная, образуют область значений функции (слайд №8)
- Независимую переменную иначе называют аргументом, а зависимую переменную называют функцией от этого аргумента (слайд №9)
- Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции (слайд №10)
(Дети оценивают себя. Учитель корректирует знания по необходимости.)
3.
Уч: Итак, вы готовы к изучению прямой пропорциональности. Вспомните примеры прямой пропорциональности, полученные при выполнении 1 задания. (слайд №11) Уч: Внимательно рассмотрев ряд, предложите свои формулы по тому же подобию.
(Дети предлагают свои формулы)
Уч: Дети, чем вы руководствовались при составлении своих формул, продолжающих ряд?
Д:
- В левой части формулы стоит произведение числа и переменной х, а в правой – переменная y.
- Переменных две.
Уч: Скажите, а являются продолжением ряда следующие формулы функций:
y=x² ; y=2x-3; y=2/x.
Д: Нет. В первой формуле функции переменная х во второй степени, а в нашем ряду переменная в первой степени; во второй – есть числовой компонент, а в нашем ряду его не должно быть; в третьей – на переменную х делят, а надо числовой коэффициент умножить на переменную х.
Уч: Ребята, а какой буквой обозначена переменная здесь существенно?
Д: Нет, можно переменную обозначить любой буквой.
Уч: А каким может быть коэффициент?
Д: Коэффициент может быть любым числом.
Уч: А как можно записать формулу прямой пропорциональности в общем виде
Д: y=аx или y= cx, где x- независимая переменная, c, а- числа
( на экране слайд)
Определение: Прямой пропорциональностью называется функция, которую можно задать формулой вида y=kx, где x - независимая переменная, k - не равное нулю число.
Уч: Определение есть у вас в учебнике на стр. 65. Выделите ключевые слова в данном определении, т. е. существенные признаки, по которым мы сможем отличать данный объект от остальных.
(Обсуждают)
4.
Уч: Итак, для того чтобы нам распознать прямую пропорциональность мы должны проверить существенные признаки. Это должна быть функция и вид её должен быть y=kx. Давайте попробуем распознавать прямую пропорциональность. Выполним упражнение на «да» и «нет». Возьмите таблицу (таблица находится на столе каждого уч-ся). Вам необходимо заполнить таблицу, ставя «+» или «-» в нужном столбце
объект функция вид y=kx Прямая пропорциональность
3x
y= 2х
Y=x-4
Y=5x²
4=7x
Y=x³/5
Y=-x
8>5x+1
Y=3/(x+2)
Y=x/2
Уч: А теперь проверим (самопроверка), что у вас получилось.
(появляется слайд №13, дети работают ручкой в таблице)
5.
Уч: А теперь, ребята, давайте построим графики функций прямой пропорциональности -из таблицы (y=2x, y= -x. y= x/2)
(Учащимся предлагается провести исследовательскую работу, ребята работают в группе по выяснению следующих вопросов:
1. Что является графиком прямой пропорциональности?
2. Как построить график прямой пропорциональности?
3. Определить этапы построения)
После чего результаты исследования обсуждаются у доски. (слайд №14)
6.
А теперь небольшая самостоятельная работа, в виде теста (слайд №15 с ответами)
(Карточка № 4 Самостоятельная работа)
Вариант 1.
Вариант 2.
1. Какая из функций, заданных формулой, является прямой пропорциональностью?
а) у = - 6х+1 б) у = 5/(х+2)
в) у = 8х г) у = – 3
1. Какая из функций, заданных формулой, является прямой пропорциональностью?
а) у = 7х+4 б) у = – 8х
в) у = 2х 2 г) у = 3
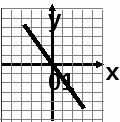
2. На каком рисунке изображен график прямой пропорциональности?
а)
б)
в)
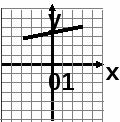
2. На каком рисунке изображен график прямой пропорциональности?
а)
б)
в)
3. В каких координатных углах находится график функции у = 1,7х? Ответ:_____
3. В каких координатных углах находится график функции у = – 2,4х? Ответ:_____
4. Велосипедист движется равномерно со скоростью 14км/ч.Напишите формулу, выражающую зависимость пройденного пути s (в км) от времени движения t(в ч).
Ответ:______
4. Мотоциклист движется равномерно со скоростью 57 км/ч.Напишите формулу, выражающую зависимость пройденного пути s (в км) от времени движения t(в ч).
Ответ:_________
5. Является ли зависимость в №4 прямой пропорциональностью?
а) да б) нет
5. Является ли зависимость в №4 прямой пропорциональностью?
а) да б) нет
(Взаимопроверка)
1вариант 2 вариант
1. в б
2. в б
3. I и III II и IV
4. s = 14t s = 57t
5. да да
Выставляют отметки за тест: 5 «+» - 5
4 «+» - 4
3 «+» - 3
Меньше трех плюсов – «Будем работать дальше».
7.
Вернемся к плану урока. Давайте посмотрим все ли пункты плана мы выполнили.
(обсуждают, подводят итог)
8. (слайд №16)
Д/з Вариант А: п.15, №297, №300(а,б,в). (для уч-ся с низкой мотивацией)
Вариант Б : п.15. №300(а,б,в), составить карточки по данной теме, которую вы могли бы предложить своему товарищу из класса. (для уч-ся среднего и выше среднего уровней)
Уч: Итак, урок закончен. А на следующем уроке мы узнаем от чего зависит расположение прямой в системе координат и познакомимся с биографией Джорджа Полиа.