Конспект урока по теме "Арифметическая прогрессия"

Данная работа представляет собой конспект урока по теме "Арифметическая прогрессия" (9 класс). В работе представленая краткая характеристика урока - методы, формы, цели и приемы обучения, а также описаны все основные этапы введения и первичного усвоения такоего понятия как арифметическая прогрессия, ее свойства и формулы вычисления n-го элемента и суммы S ее первых элементов.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Конспект урока по теме "Арифметическая прогрессия" »

Конспект урока по алгебре в 9 классе

по теме «Арифметическая прогрессия»

Учитель: Карпеева О. В.

Класс: 9

Тема урока: Арифметическая прогрессия.

Тип урока: Урок изучения нового.

Вид урока: комбинированный

Учебная задача: Сформулировать определение арифметической прогрессии и вывести все формулы,

связанные с этим понятием.

Тип урока: проблемно – развивающий.

Тип обучения: личностно – ориентированный.

Цели урока:

1. Образовательные:

Сформулировать определение, свойство и признак арифметической прогрессии;
Вывести формулы n - го члена и суммы n первых членов арифметической прогрессии.

2. Развивающие:

Формирование абстрактного мышления;
Развитие умения сравнения, проводить аналогию;
Развитие гибкости мышления.

3. Воспитательные:

Развить умение высказывать свою точку зрения;

Развитие умения аргументирования своего высказывания;

Дидактическая единица: определение, теорема.

Познавательные средства: сравнение, аналогия, метод неполной индукции.

Формы обучения:

Индивидуальная (при выводе формул – выборочная проверка);
Фронтальная (при повторении и закреплении);
Коллективная (при формулировании определения, свойства и признака арифметической прогрессии – проверка типа консультации).

Методы обучения:

По источнику получения знаний:
- Словесный (рассказ учителя);
- Наглядный (заполнение таблицы);
- Практический (выполнение упражнений).
По характеру учебной деятельности:

Проблемное изложение (выяснить способ вычисления Гаусса);
Частично – поисковый (формулы выводятся под руководством учителя).

По дидактическим целям:

Метод приобретения знаний.

По содержанию учебного материала:

Метод первичного усвоения учебного материала.

Средства обучения: экран, ПК.

Структура урока:

Организационный момент – 1 мин.
Активизация прежних знаний – 2 мин.
Изучение нового материала:

Постановка проблемы – 1 мин.
Решение проблемы – 29 мин.

Закрепление – 5 мин.
Подведение итогов – 1 мин.
Домашнее задание – 1 мин.

1 этап. Активизация прежних знаний.

Действия учителя	Действия ученика	Записи на доске	Записи в тетрадях
С какими понятиями вы познакомились на предыдущих уроках?	Числовые последовательности
Приведите пример числовой последовательности	Последовательность натуральных чисел Последовательность четных чисел
Какими способами задаются числовые последовательности?	Числовая последовательность может быть задана: С помощью перечисления; С помощью формулы «n» - го слагаемого; Рекуррентным способом
Какие виды числовых последовательностей вам известны?	Последовательности бывают: Конечные и бесконечные; Убывающие и возрастающие
Сегодня мы с вами познакомимся еще с одним видом числовой последовательности. В тетрадях записываем число и оставим место для темы урока, которую вы мне сформулируете немного попозже. Но сначала послушайте следующую историю.	Записывают число.

2 этап. Постановка проблемы.

Действия учителя	Действия ученика	Записи на доске	Записи в тетрадях
Задача. Известный немецкий математик Карл Гаусс в детстве был непоседливым мальчиком, и учитель никак не мог с ним справиться. И вот однажды, чтобы Гаусс успокоился, учитель задал ему задачу: вычислить сумму первых ста натуральных чисел. Буквально через минуту Гаусс дал правильный ответ. Вопрос: чему равна сумма и как Гаусс так быстро ее вычислил?
Давайте и мы вычислим искомую сумму. Для этого выпишем слагаемые.	1 + 2 + 3 + …. + 100	1 + 2 + 3 + … + 100 - ?	1 + 2 + 3 +…. + 100 - ?
Что образуют слагаемые?	Числовую последовательность
Чтобы ответить на вопрос задачи необходимо изучить свойства данной последовательности.

3 этап. Решение проблемы.

Действия учителя	Действия ученика	Записи на доске	Записи в тетрадях
Попытаемся выделить и сформулировать эти свойства.
Итак, как можно получить второй член это последовательности?	Чтобы получить второй член последовательности необходимо к первому члену прибавить единицу
А третий член?	Необходимо ко второму члену прибавить единицу
То есть, каждый член последовательности равен предыдущему, сложенному с некоторым числом
Сформулируем еще раз черты этих слагаемых	Они образуют числовую последовательность; Каждый член равен предыдущему , сложенному с некоторым числом
Скажите, а первый член последовательности мы можем получить таким образом?	Нет, т. к . для него нет предыдущего
А некоторое число, которое мы прибавляем будет одинаковым для всех слагаемых и разным	Одинаковым
Тогда уточните свои утверждения	Каждый член, начиная со второго равен предыдущему, сложенному с одним и тем же числом
Последовательность, которая обладает такими чертами и будет называться арифметической прогрессией. Сформулируйте тему урока.	Арифметическая прогрессия.	Арифметическая прогрессия	Арифметическая прогрессия
Попытайтесь сформулировать определение арифметической прогрессии	Арифметическая прогрессия – это числовая последовательность, каждый член которой, начиная со второго равен предыдущему, сложенному с одним и тем же числом.		Арифметическая прогрессия – это числовая последовательность, каждый член которой, начиная со второго равен предыдущему, сложенному с одним и тем же числом.

Действия учителя

Действия ученика

Записи на доске

Записи в тетрадях

Если использовать математическую символику, то определение арифметической прогрессии можно записать в следующем виде:

a₁, a₂, …., a_n - числовая последовательность, где

a_n₊₁ = a_n + d

a₁, a₂, …., a_n - числовая последовательность, где

a_n₊₁ = a_n + d

Выразите из формулы число «d»

d = a_n+1 - a_n

Число «d» принято называть разностью арифметической прогрессии Что такое разность арифметической прогрессии?

Разностью арифметической прогрессии – это разность между следующим и предыдущим членом арифметической прогрессии.

d – разность

Как вы думаете, почему назвали разностью?

Потому что вычисляется с помощью разности.

Каким числом может быть разность?

Разность может быть любым числом

d – любое число

Используя, слагаемые нашей последовательности заполним следующую таблицу

Комментируют заполнение таблицы

n	a_n-1	a_n	a_n+1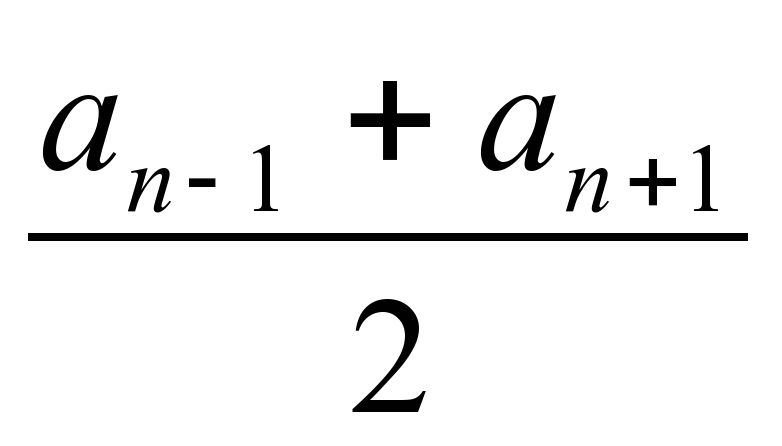
1	--	--	---	---
2	1	2	3	2
3	2	3	4	3
4	3	4	5	4

n	a_n-1	a_n	a_n+1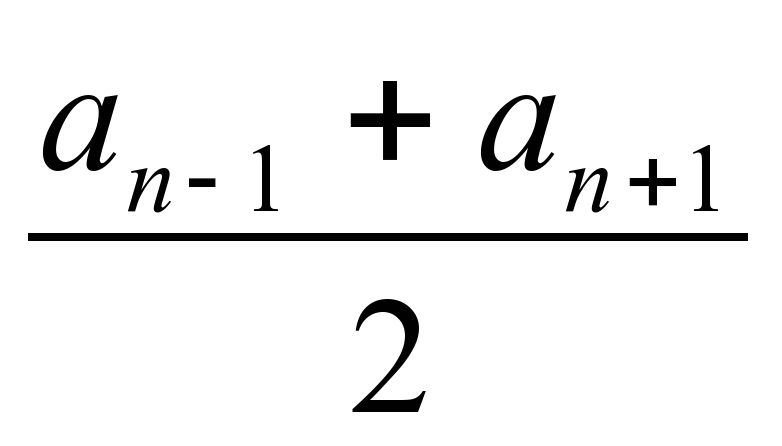
1	--	--	---	---
2	1	2	3	2
3	2	3	4	3
4	3	4	5	4

Сравните 3 и 5 столбцы. Каковы значения в этих столбцах?

Значения в 3 и 5 столбцах совпадают

Какое предположение можно сформулировать?

Каждый член арифметической прогрессии, начиная со второго равен среднему арифметическому двух соседних с ним членов

Это утверждение является свойством арифметической прогрессии. Запишем формулировку словами и математическими символами

Действия учителя	Действия ученика	Записи на доске	Записи в тетрадях
Как вы думаете почему прогрессия называется именно арифметической?	Потому что члены прогрессии равны среднему арифметическому.
Попытайтесь сформулировать утверждение, обратное свойству	Если в числовой последовательности, каждый член, начиная со второго равен среднему арифметическому двух соседних с ним членов, то эта последовательность является арифметической прогрессией
Сформулированное утверждение представляет собой признак арифметической прогрессии. Запишите формулировку в тетрадь.			Если в числовой последовательности, каждый член, начиная со второго равен среднему арифметическому двух соседних с ним членов, то эта последовательность является арифметической прогрессией
Следовательно, как можно доказать что последовательность является арифметической прогрессией?	Можно доказать это с помощью определения или с помощью признака
Скажите, в условии задачи арифметическая прогрессия каким способом задана?	Арифметическая прогрессия задается с помощью перечисления
А в определении?	Рекуррентным способом
Попытаемся теперь вывести формулу «n» - го слагаемого арифметической прогрессии, если известны а₁ и d
Как вычислить второй член арифметической, если известен первый член и разность арифметической прогрессии	К первому члену прибавить разность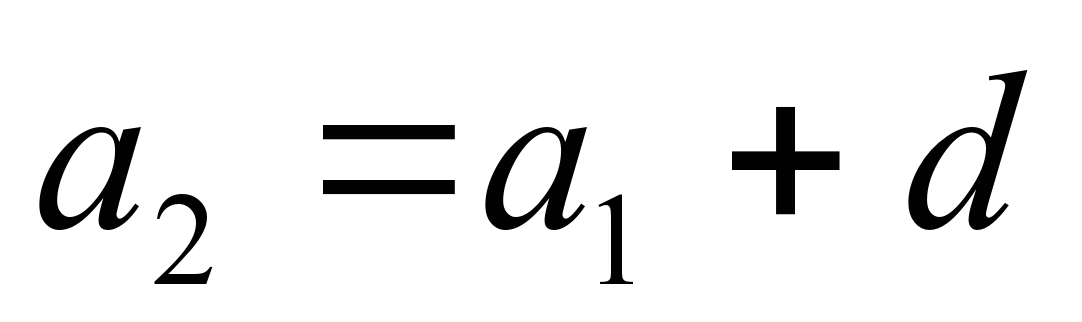
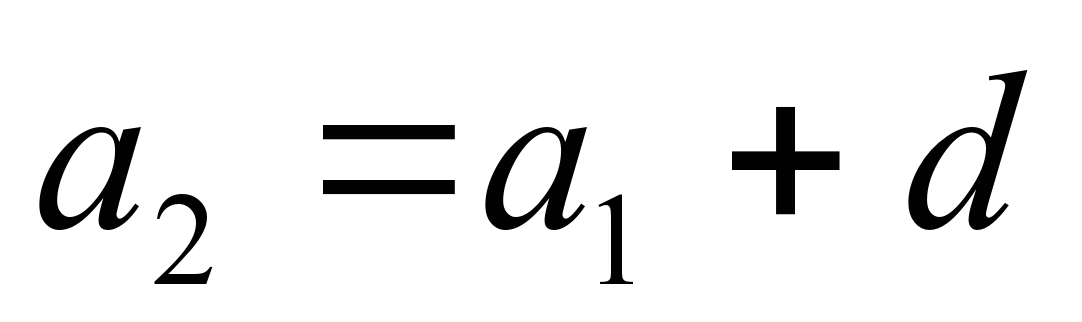Как вычислить третий?	Комментируют вычисления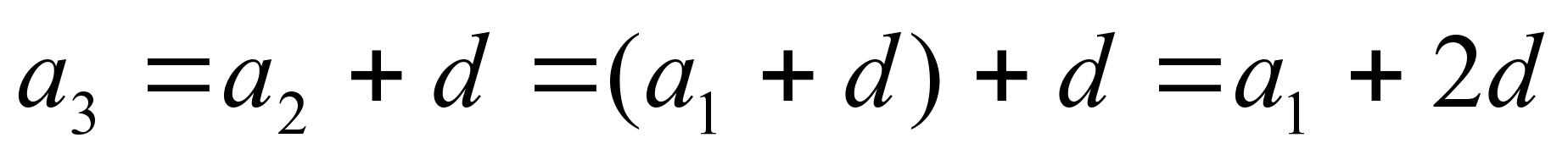
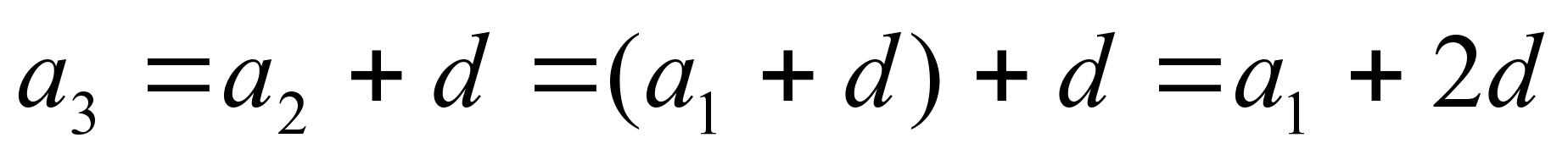
Выразите четвертый член через первый член и разность	Комментируют вычисления
Сравните теперь номер искомого члена и коэффициент, стоящий при разности в полученных формулах	Коэффициент при разности на единицу меньше, чем номер искомого члена

Действия учителя	Действия ученика	Записи на доске	Записи в тетрадях
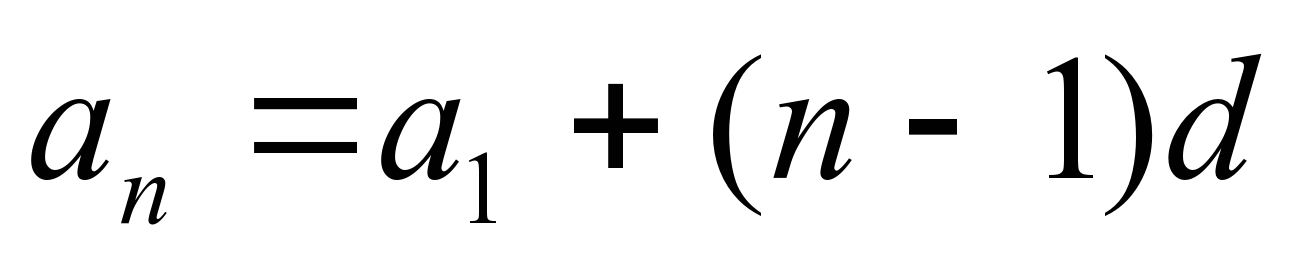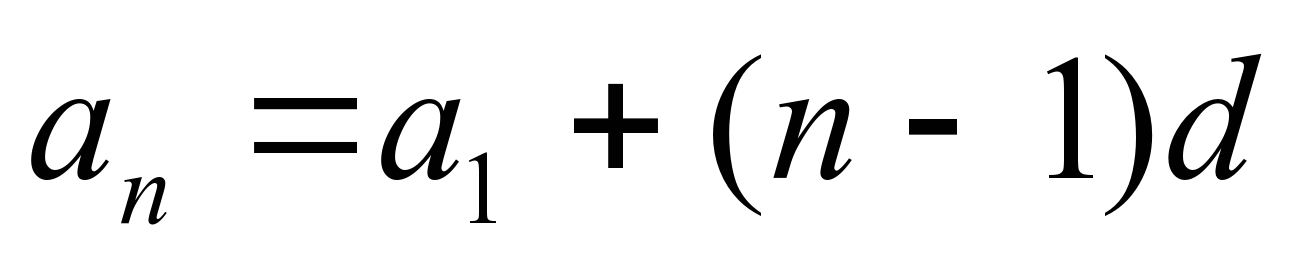Как по вашему, мы должны записать формулу «n» - го слагаемого арифметической прогрессии	Диктуют формулу	- формула «n» - го слагаемого	- формула «n» - го слагаемого
В исходной задаче требуется найти сумму: 1 + 2 + 3 + .. + 100. Мы выяснили, что слагаемые данной числовой последовательности образуют арифметическую прогрессию.
Чему равен первый член?	1	а₁= 1	а₁= 1
Сколько всего членов?	100	n= 100	n= 100
Чему равен последний член?	100	а₁₀₀ = 100	а₁₀₀ = 100
Давайте найдем способ вычисления суммы n первых членов арифметической прогрессии, если известны первый и последний член прогрессии, а также число слагаемых. Этим способом и воспользовался Гаусс для решения задачи.
Учитель с помощью кодоскопа выводит формулу суммы первых слагаемых арифметической прогрессии	Учащиеся записывают вывод формулы	- формула суммы первых членов арифметической прогрессии	- формула суммы первых членов арифметической прогрессии
Используя выведенную формулу, какой же ответ дал Гаусс своему учителю?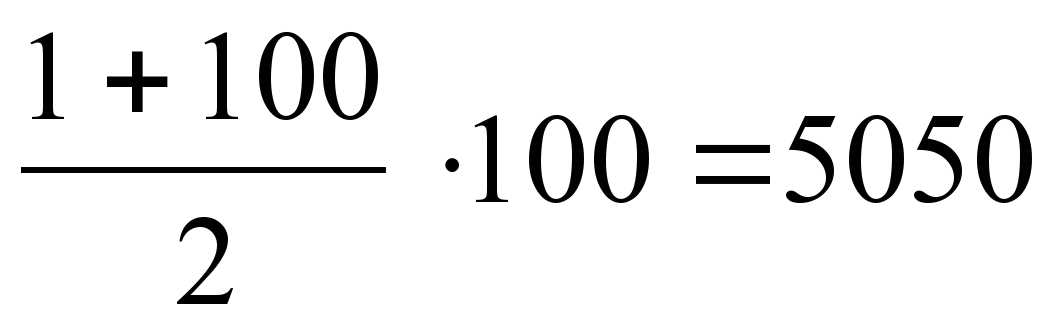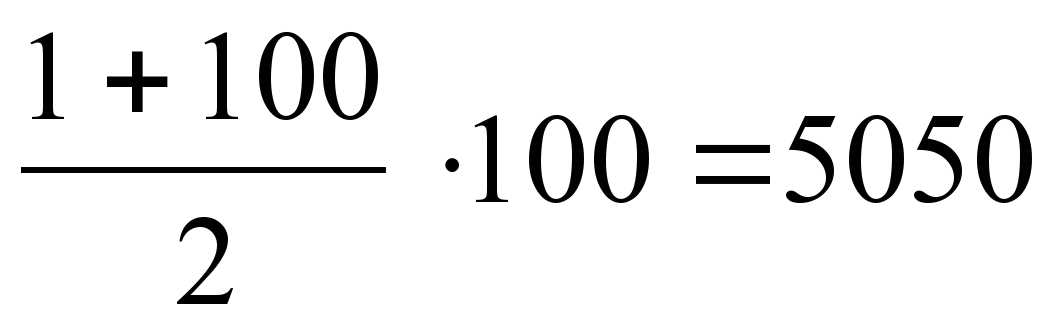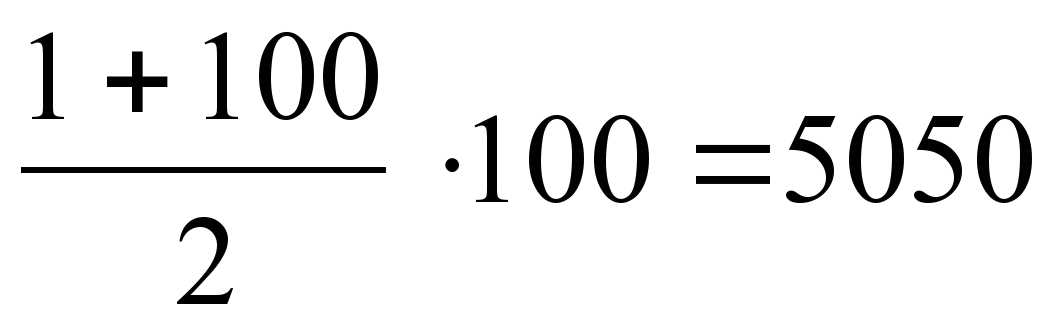
Если объединить формулу n – го члена и формулу суммы, то можно получить еще одну формулу вычисления суммы первых слагаемых. В этой формуле используются первый член, разность и количество слагаемых.	Учащиеся выводят еще одну формулу	- формула суммы первых членов арифметической прогрессии	- формула суммы первых членов арифметической прогрессии

4 этап. Закрепление.

Действия учителя	Действия ученика	Записи на доске	Записи в тетрадях
Итак, с каким видом числовых последовательностей вы сегодня познакомились?	Арифметическая прогрессия
Какая последовательность называется арифметической прогрессией?	Арифметическая прогрессия – это числовая последовательность, каждый член которой, начиная со второго равен предыдущему, сложенному с одним и тем же числом.

Действия учителя	Действия ученика	Записи на доске	Записи в тетрадях
Что такое разность арифметической прогрессии?	Разностью арифметической прогрессии – это разность между следующим и предыдущим членом арифметической прогрессии.
Среди числовых последовательностей выберите те, которые являются арифметическими прогрессиями, и назовите в них разность.	Данная числовая последовательность является арифметической прогрессией, т. к. каждый ее член равен предыдущему сложенному с 2, таким образом, d = 2.	2, 4, 6, 8,….. - арифметическая прогрессия: d = 2.	2, 4, 6, 8,…..- арифметическая прогрессия: d = 2.
	Эта последовательность не является арифметической прогрессией, т. к. ее члены не равны сумме предыдущего члена с одним и тем же числом.	5, 6, 8, 3, …. – не арифметическая прогрессия	5, 6, 8, 3, …. – не арифметическая прогрессия
	Последовательность является арифметической прогрессией, т. к. члены получаются путем сложения предыдущего члена с – 1, т. е. d = -1.	- 1, - 2, - 3, - 4,…… - арифметическая прогрессия, d = -1.	- 1, - 2, - 3, - 4,…… - арифметическая прогрессия, d = -1.
	Последовательность является арифметической прогрессией с разность 0.	4, 4, 4, 4, ….. – арифметическая прогрессия, d = 0.	4, 4, 4, 4, …. – арифметическая прогрессия, d = 0.
С помощью какого утверждения можно выяснить, что данная последовательность является арифметической прогрессией?	С помощью определения или с помощью признака арифметической прогрессии.
Сформулируйте признак арифметической прогрессии	Если в числовой последовательности, каждый член, начиная со второго равен среднему арифметическому двух соседних с ним членов, то эта последовательность является арифметической прогрессией
Каким свойством обладает арифметическая прогрессия?	Каждый член арифметической прогрессии, начиная со второго равен среднему арифметическому двух соседних с ним членов
Какими способами можно задать арифметическую прогрессию?	С помощью перечисления, рекуррентным способом или с помощью формулы «n» - го члена.
Чтобы вычислить сумму первых n членов арифметической прогрессии, какие элементы последовательности необходимо знать?	Чтобы вычислить сумму первых n членов арифметической прогрессии необходимо знать первый, n – ный члены и номер или первый член, номер и разность прогрессии.