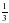Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Конспект урока на тему: "Деление положительных и отрицательных чисел."
Тема: Деление положительных и отрицательных чисел.
Цели:
Образовательные: отработка умений и навыков при сложении, вычитании, умножении и делении чисел с разными знаками путём применения разнообразных форм упражнений (решении примеров, уравнений, упрощении выражений).
Развивающие: формировать навыки самостоятельной работы; развивать логическое мышление, вычислительные навыки; расширение кругозора.
Воспитательные: воспитание познавательного интереса к предмету; воспитывать культуру труда, математической речи, активность, самостоятельность, культуру общения.
Ход урока:
1. Организационный момент.
Приветствие учеников.
Проверь-ка, дружок,
Ты готов начать урок?
Все ль на месте,
Все в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
2. Мотивация урока.
Едва ли не самым тёмным для учащихся местом в математике является учение о действиях с отрицательными числами. И это не потому, что устанавливаемые правила действий сложны. Напротив, они очень просты. Но тёмными остаются два вопроса:
1) Зачем вводятся отрицательные числа?
2) Почему над ними совершаются действия по таким-то правилам, а не по иным? В частности, очень плохо понимается, почему при умножении и делении отрицательного числа на отрицательное результат есть положительное число.
Все эти вопросы возникают потому, что с отрицательными числами учащихся обычно знакомят до того, как они начали решать уравнения, и больше не возвращаются к правилам действий с отрицательными числами. Между тем лишь в связи с решением уравнений выясняется ответ на оба поставленных выше вопроса. Исторически отрицательные числа возникли именно в этой связи. Не будь уравнений, не было бы нужды и в отрицательных числах.
Долгое время уравнения изучались без помощи отрицательных чисел; при этом возникали многие неудобства; для устранения этих неудобств и были введены отрицательные числа. При этом в течение долгого времени многие выдающиеся математики отказывались вводить их в употребление или вводили с большой неохотой. Ещё Декарт (1596–1650) называл отрицательные числа “ложными числами”.
Таким примерно образом и были введены отрицательные числа; цель этого — рационализация вычислительного процесса; правила действий над отрицательными числами явились результатом введения этого рационализаторского приёма в вычислительную практику.
Многолетние и многообразные испытания показали, что этот приём обладаем огромной эффективностью и находит себе блестящие применения во всех областях науки и техники. Всюду введение отрицательных чисел позволяет охватить единым правилом такие явления, для которых нужно было бы выдумывать десятки правил, если ограничиться числами положительными.
Итак, на два выше поставленных вопроса нужно ответить следующим образом:
1) отрицательные числа вводятся затем, чтобы устранить ряд трудностей, возникших прежде всего при решении уравнений;
2) правила действий над ними вытекают из необходимости согласовать результаты, полученные с помощью отрицательных чисел, с теми результатами, которые могли бы быть получены и без них.
3. Актуализация опорных знаний.
Устный счет
Записать только ответы:
1) -12-18
2) -20+10
3) Найти модуль -6
4) (-2)
5) Заменить неправильной дробью31/5
6) Заменить десятичной дробью 2/5
7) 5,2:1,3
8) - (а+в)
9) – (-а-в)
10) : 2
11) Заполнить схему
(-)(-)=
(-)(+)=
(-)(-)=
12)Какие примеры мы пока еще не сможем решить? (на деление)
Дети поочерёдно выполняют устные примеры с рациональными числами:
4. Изучение нового материала
1.Деление отрицательных чисел объясняю:
12:3=
-12:(-4)=
Образец записи:
-4,5:(-1,5)=
-2/3:(-4/5)=
Вывод сделать самостоятельно и проверить по учебнику.
2)Деление чисел с разными знаками объясняют дети: -24:3=
Образец записи показывают дети: -2/3:3/4=
-13/5:11/3=
3) 0:(-6)=?
-7:0=? Вывод.
4)Заполнить схему: (-):(-)=
(+):(-)=
(-):(+)=
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
При делении чисел с разными знаками, надо:
1) разделить модуль делимого на модуль делителя;
2) поставить перед полученным числом знак ?.
Делить на нуль нельзя!
5. Физкультминутка.
Минутка отдыха. Гимнастика для глаз
Вертикальные движения глаз вверх-вниз.
Горизонтальное вправо-влево.
Вращение глазами по часовой стрелке и против.
Закрыть глаза и представить по очереди цвета радуги как можно отчётливее.
Глазами «нарисовать» кривую, изображённую на доске несколько раз, сначала в одном, а затем в другом направлении.
6. Закрепление нового материала:
решить
№ 1131, 1136 (устно), 1132 (1-7), 1134 (1-4), 1137(1).
Работа в парах:
1. -57+(-19)
2. 1,7-5,8
3.-5/8-7/12
4. -3+12/5
5. 55/14-(31/2-5/7)
6.-8,65*0
7.-5/9*(-12/25)
8.11/8*(-51/3)
9 .48:(-16)
10. 4/9:(-8)
11. 5,25:(-1/20)
12. (-3)2*(-2)3
7. Самостоятельная работа.
Решить № 1137 (2). 1135 (6).
8. Итоги урока. Д/з. Рефлексия.
Решить на 7 баллов: № 1133(1-7), на 11 баллов: № 1138 (1, 2), 1135 (1-4).
Учащиеся по кругу высказываются одним предложением.
• Я научился…
• Было трудно…
• Сегодня я узнал…
• У меня получилось…
• Теперь я могу…
Помни всегда
Что без труда
В учебе побед не добиться
Слышим звонок начат урок
К финишу мчимся как птицы
Только в труде
Знанья приходят к тебе
Может сейчас, здесь среди нас
Будущих лет Пифагоры.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Конспект урока на тему: "Деление положительных и отрицательных чисел." »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1970 руб.
2820 руб.
2000 руб.
2860 руб.
1970 руб.
2820 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

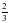 : 2
: 2