Сценарий урока.
Подготовка к уроку начинается сразу после изучения признаков равенства треугольников. Ребятам выдаются следующие задания:
«История возникновения задач на построение»,
- «Знаменитые задачи древности»,
- «Построение на местности»,
- «Применение бумаги в задачах на построение»,
- «Использование симметрии в задачах на построение».
- Журналистам поручается найти ответы и провести опрос «населения» по заранее подготовленным вопросам. Примеры вопросов:
- Какой знаменитый математик древности впервые начал решать в геометрии задачи на построение?
- Какие задачи в математике называют задачами на построение?
- Какими инструментами разрешено пользоваться при решении задач на построение?
- Известно, что в древнем Египте землемеров называли гарпедонаптами. По преданию, гарпедонапты выработали практическую геометрию, занимаясь обмером земельных участков и фундаментов строений. При помощи какого прибора они это делали? И т.д.
- Несколько журналистов «выезжают» в командировку по письмам «читателей». В редакцию журнала пришли письма:
- Дорогой журнал! Помогите, пожалуйста, разделить участок на четыре одинаковые по форме и размерам участка, так, чтобы на каждом был колодец. Садоводы кооператива «ЮГАНЕЦКИЙ».(Участок имеет форму равностороннего треугольника).
Рис.1
- Дорогой журнал! Срочно нужна ваша помощь. Две наши деревни находятся на одном и том же берегу реки и на разных расстояниях от нее. Где нам следует построить мост через реку, что бы он отстоял от этих деревень на одинаковом расстоянии?
- Дорогой журнал! Пишут вам ребята из села Ильинского. Мы занимаемся в туристическом кружке и в каникулы отправляемся в поход на озеро Светлое. В поход мы отправляемся с заданием измерить длину озера. Подскажите, как это сделать.
Ход урока:
- Организация начала занятия. Подготовка учащихся к работе. Готовность класса и оборудования
- Реализация сюжета игры.
- Здравствуйте ребята! Сегодня мы завершаем наше журналистское расследование «Как построить, чтобы боги были довольны?». Убедимся, какое важное практическое применение имеет материал сегодняшнего урока. Наши журналисты хорошо поработали, и сегодня нам предстоит познакомиться с их материалом, получить ответ на главный вопрос и подготовить материалы к публикации.
В нашем журнале существуют отделы:
- отдел исторической информации;
- отдел по связям с общественностью;
- проблемный отдел;
- информационный отдел;
- экспертный отдел.
Учитель объявляет учащихся, которые назначаются помощниками главного редактора (2-3 человека).
- Повторение изученного. Актуализация знаний.
Давайте вспомним, какие задачи на построение мы решали на уроках геометрии. Задание - надо сопоставить картинку с задачей.
В результате расследования созданы презентации:
- «Как возникли задачи на построение?»
- «Знаменитые задачи древности»
- «Построение на местности»
- «Роль бумаги при решении задач на построение»
- «Симметрия и построения».
Ребятам предлагается ответить на вопрос: «Можешь ли ты построить так, чтобы боги были довольны?». Для этого выдаются варианты ответа на вопрос, из которых надо выбрать один ответ.
Выбери один или два самых подходящих ответа, на твой взгляд, на вопрос.
- Да, могу.
- Некоторые задачи могу.
- Могу, но только с помощью учителя или товарища.
- Не могу, т.к. не понял эту тему.
Рис 8.
- Информация о домашнем задании.
Сценарий урока.
Подготовка к уроку начинается сразу после изучения признаков равенства треугольников. Ребятам выдаются следующие задания:
- Подготовить презентации по темам:
- «История возникновения задач на построение»,
- «Знаменитые задачи древности»,
- «Построение на местности»,
- «Применение бумаги в задачах на построение»,
- «Использование симметрии в задачах на построение».
- Журналистам поручается найти ответы и провести опрос «населения» по заранее подготовленным вопросам. Примеры вопросов:
- Какой знаменитый математик древности впервые начал решать в геометрии задачи на построение?
- Какие задачи в математике называют задачами на построение?
- Какими инструментами разрешено пользоваться при решении задач на построение?
- Известно, что в древнем Египте землемеров называли гарпедонаптами. По преданию, гарпедонапты выработали практическую геометрию, занимаясь обмером земельных участков и фундаментов строений. При помощи какого прибора они это делали? И т.д.
- Несколько журналистов «выезжают» в командировку по письмам «читателей». В редакцию журнала пришли письма:
- Дорогой журнал! Помогите, пожалуйста, разделить участок на четыре одинаковые по форме и размерам участка, так, чтобы на каждом был колодец. Садоводы кооператива «ЮГАНЕЦКИЙ».(Участок имеет форму равностороннего треугольника).
Рис.1
- Дорогой журнал! Срочно нужна ваша помощь. Две наши деревни находятся на одном и том же берегу реки и на разных расстояниях от нее. Где нам следует построить мост через реку, что бы он отстоял от этих деревень на одинаковом расстоянии?
- Дорогой журнал! Пишут вам ребята из села Ильинского. Мы занимаемся в туристическом кружке и в каникулы отправляемся в поход на озеро Светлое. В поход мы отправляемся с заданием измерить длину озера. Подскажите, как это сделать.
Ход урока:
- Организация начала занятия. Подготовка учащихся к работе. Готовность класса и оборудования
- Реализация сюжета игры.
- Здравствуйте ребята! Сегодня мы завершаем наше журналистское расследование «Как построить, чтобы боги были довольны?». Убедимся, какое важное практическое применение имеет материал сегодняшнего урока. Наши журналисты хорошо поработали, и сегодня нам предстоит познакомиться с их материалом, получить ответ на главный вопрос и подготовить материалы к публикации.
В нашем журнале существуют отделы:
- отдел исторической информации;
- отдел по связям с общественностью;
- проблемный отдел;
- информационный отдел;
- экспертный отдел.
Учитель объявляет учащихся, которые назначаются помощниками главного редактора (2-3 человека).
- Повторение изученного. Актуализация знаний.
Давайте вспомним, какие задачи на построение мы решали на уроках геометрии. Задание - надо сопоставить картинку с задачей.
- Докладывают журналисты из отдела исторической информации.
- Историческая справка – задача об определении расстояния до корабля. Докладывает журналист.
Идет обсуждение задачи.
Рис.2
- Историческая справка – построение прямого угла с помощью веревки с двенадцатью узлами. Докладывает журналист.
- «Отдыхательная пауза» - зарядка для глаз и отгадывание фигур. Фигуры: круг, квадрат, равносторонний треугольник, прямоугольный треугольник.
- Проблемный отдел.
Задача №1. Вместе с учителем решаем задачу на построение серединного перпендикуляра к отрезку. Ход решения: анализ задачи, выполнение построения, доказательство.
- Проблемный отдел.
Задача №2. Решаем задачу вместе с учителем. (Ребята сами догадываются, что для построения используется то свойство треугольника, что его высоты пересекаются в одной точке.)
- Отдел по связям с общественностью. Докладывает журналист, побывавший в командировке.
- Проверка изученности материала.
Экспертный отдел.
Мы находимся в экспертном отделе. Если есть возможность, то учащиеся работают за компьютерами, либо карточки расследований выдаются для работы всем учащимся. Работают помощники главного редактора.
Задача 1. (1 уровень)
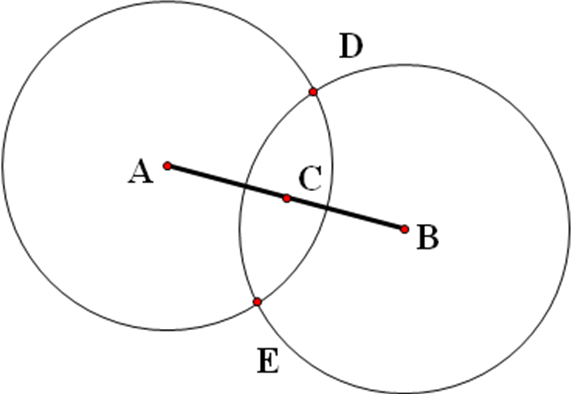
Сделай анализ задачи, выполни построение и доказательство: На рисунке даны две окружности с общим центром в точке О. Отрезки АВ и CD равны. Какие пары точек надо соединить, чтобы получились равные треугольники?
Рис.6
Задача 2. (2 уровень)
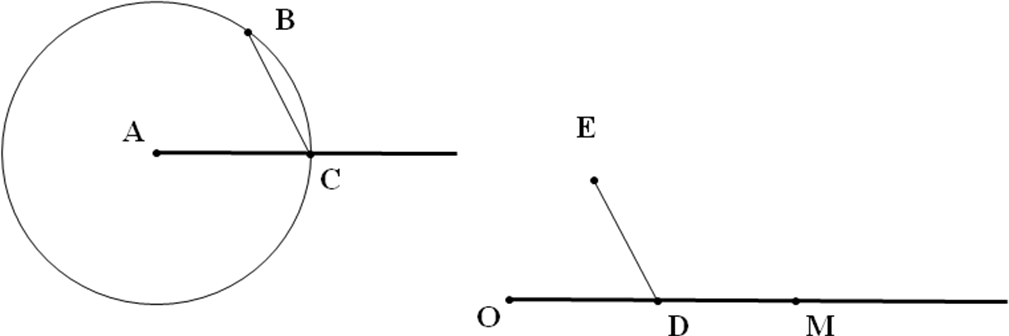
Сделай анализ задачи, выполни построение и доказательство: Точка А на рисунке изображает местонахождение элеватора, В и С двух колхозов. Луч АЕ – дорога на элеватор. Найдите на дороге АЕ точку М – где удобно построить мельницу, которая равноудалена от колхозов В и С.
.
Задача 3. (3 уровень)
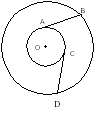
Сделай анализ задачи, выполни построение: Вершина В треугольника АВС не уместилась на листе бумаги, так, как показано на рисунке. Как построить высоту из вершины В на сторону АС.
Итоги подведения урока. Выставление оценок.
В результате расследования созданы презентации:
- «Как возникли задачи на построение?»
- «Знаменитые задачи древности»
- «Построение на местности»
- «Роль бумаги при решении задач на построение»
- «Симметрия и построения».
Ребятам предлагается ответить на вопрос: «Можешь ли ты построить так, чтобы боги были довольны?». Для этого выдаются варианты ответа на вопрос, из которых надо выбрать один ответ.
Выбери один или два самых подходящих ответа, на твой взгляд, на вопрос.
- Да, могу.
- Некоторые задачи могу.
- Могу, но только с помощью учителя или товарища.
- Не могу, т.к. не понял эту тему.
Рис 8.
- Информация о домашнем задании.
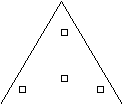 Рис.1
Рис.1





 И
И 















