Тема: “Сложение и вычитание дробей с разными знаменателями”
Цель урока: ввести правило сложения и вычитания дробей с разными знаменателями, сформировать первичные умения и навыки сложения и вычитания дробей с разными знаменателями.
Задачи:
- обучающие повторить правила приведения дробей к общему знаменателю, сравнения дробей с разными знаменателями, сложения и вычитания дробей с одинаковыми знаменателями, ввести правило сложения и вычитания дробей с разными знаменателями, применить данное правило при нахождении значений выражений.
-развивающие развивать: память, внимание, мышление, воображение, речь, навыки работы с учебником, формировать умение работать по словесной инструкции и образцу, способствовать развитию умения выделять главную мысль.
-воспитательные развивать самостоятельность, добросовестность и аккуратность, повышать познавательную активность, содействовать воспитанию интереса к математике.
Тип урока урок изучения нового материала.
Формы работы учащихся индивидуальная, фронтальная, работа в парах.
Необходимое техническое оборудование компьютер, проектор, экран.
Ход урока.
Организационный момент, контроль домашнего задания. (слайд 1)
Эпиграфом к сегодняшнему уроку служат слова Л.Н. Толстого «Человек подобен дроби: в знаменателе — то, что он о себе думает, в числителе — то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь».
Как вы понимаете эти слова?
Сегодня на уроке мы продолжим изучать обыкновенные дроби.
Актуализация знаний, устный счет.
Прежде чем приступить к изучению новой темы проведем повторение.
(слайд 2)
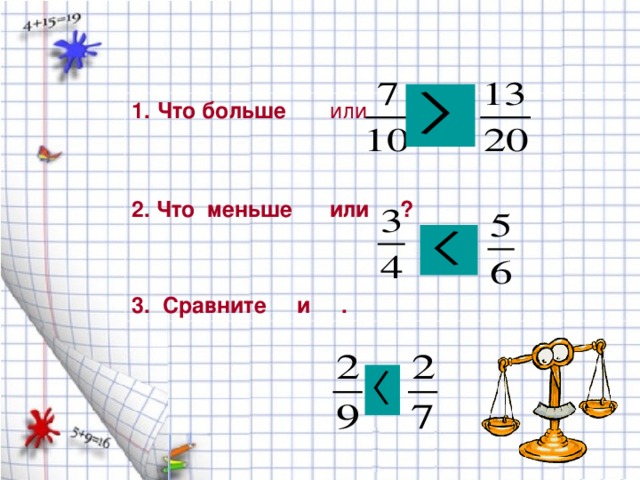
а
) Приведите дроби к наименьшему общему знаменателю:
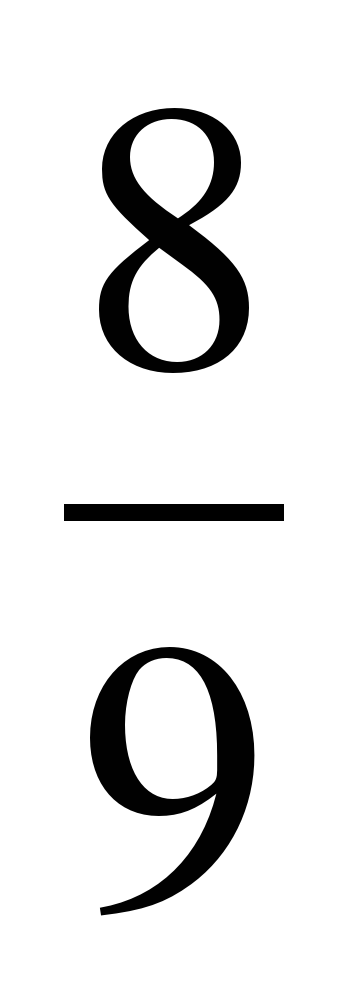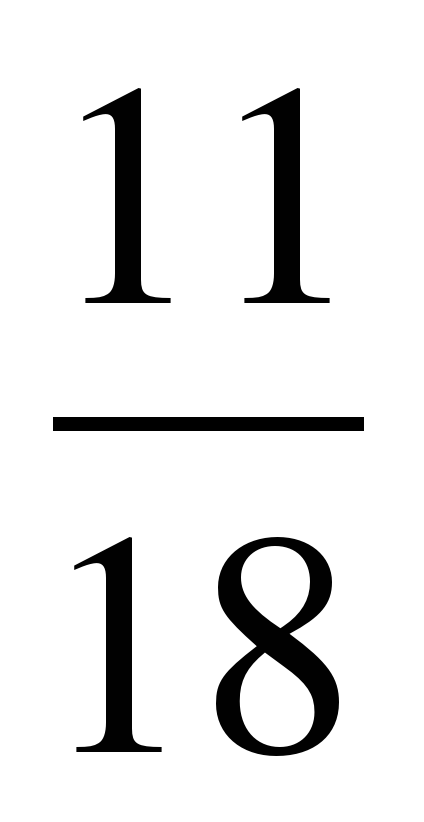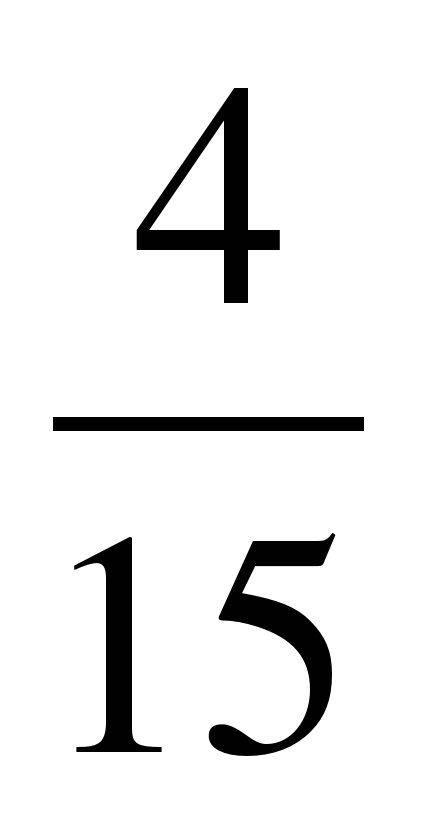и 
; 
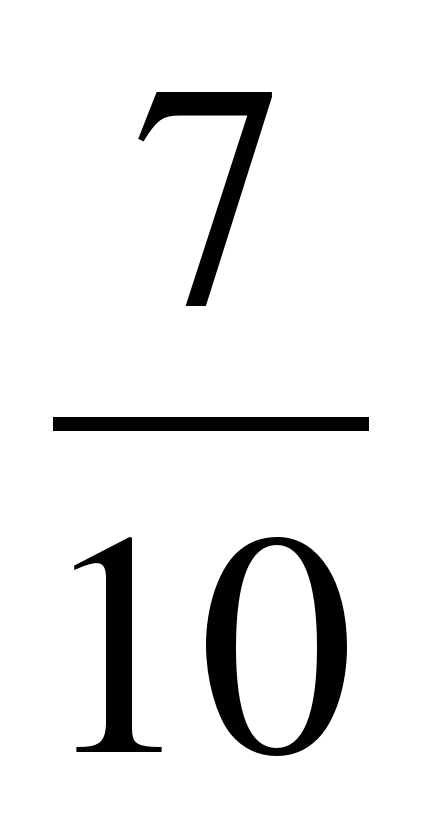и 
; 
и.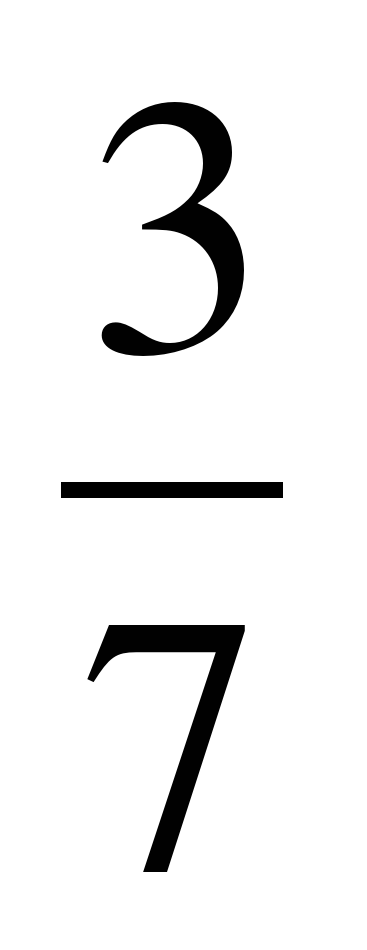 
(слайд 3)
б) Сравните дроби:
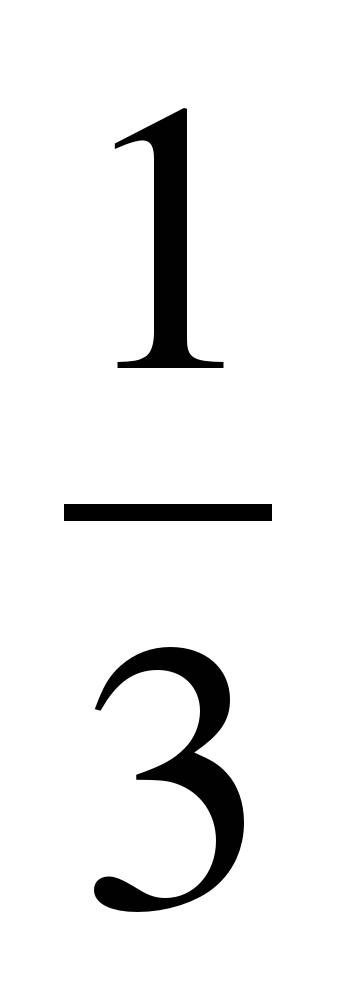и 
; 
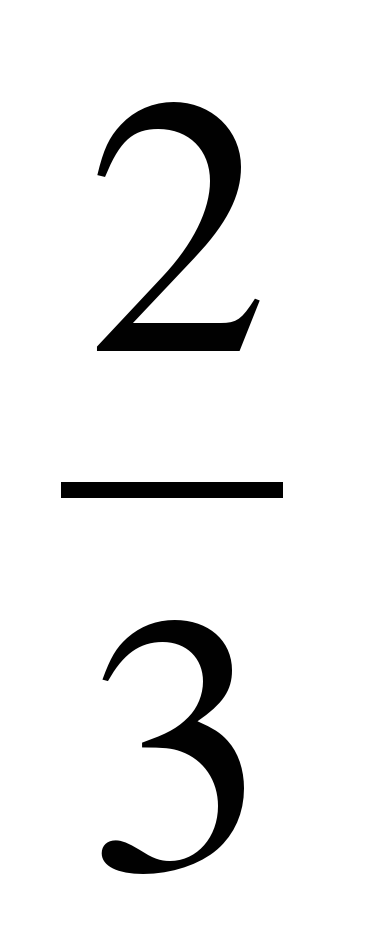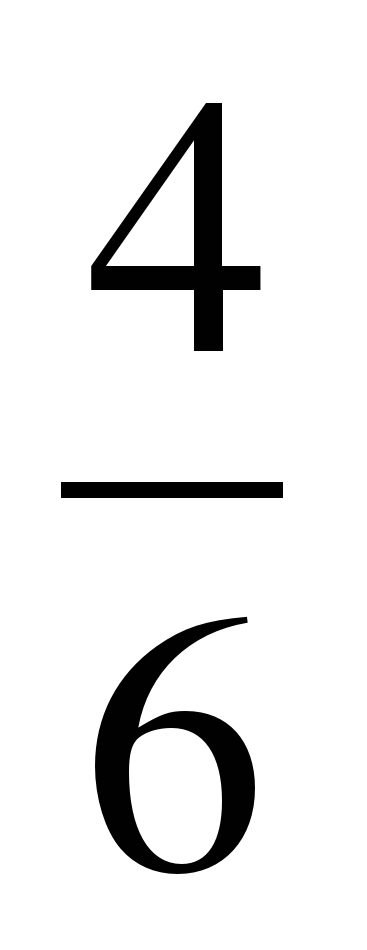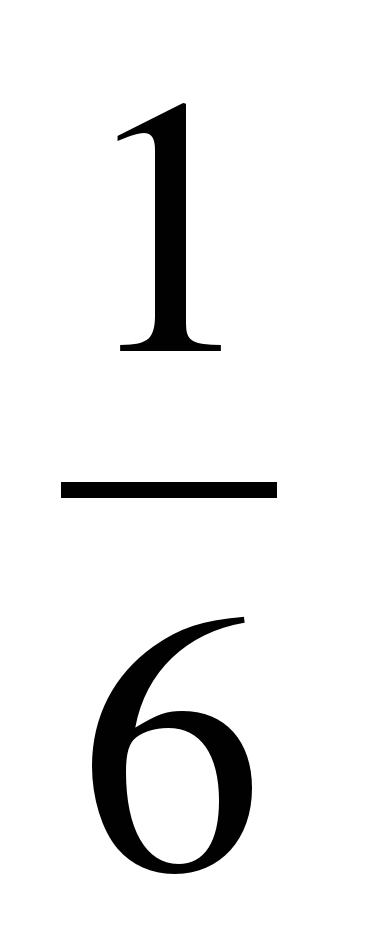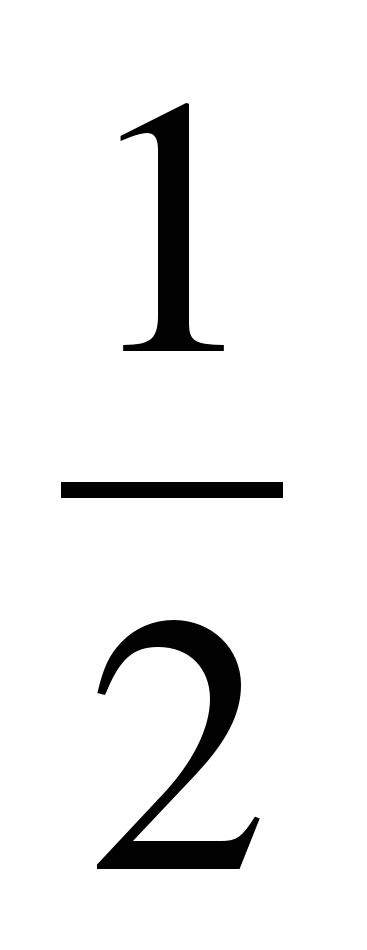и 
; 
и .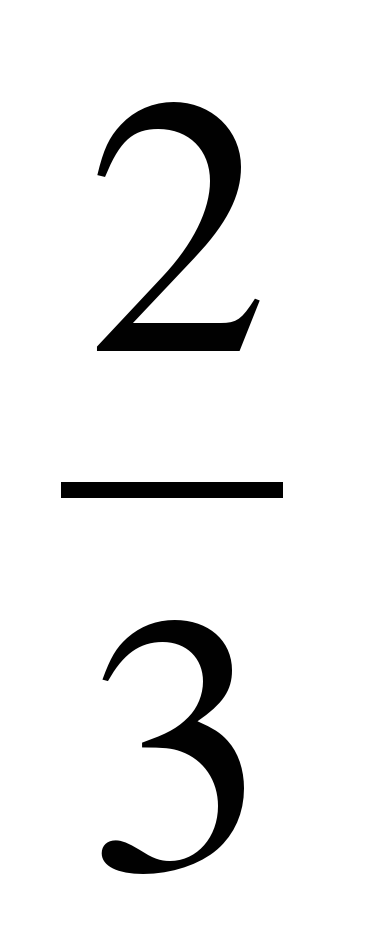
(слайд 4)
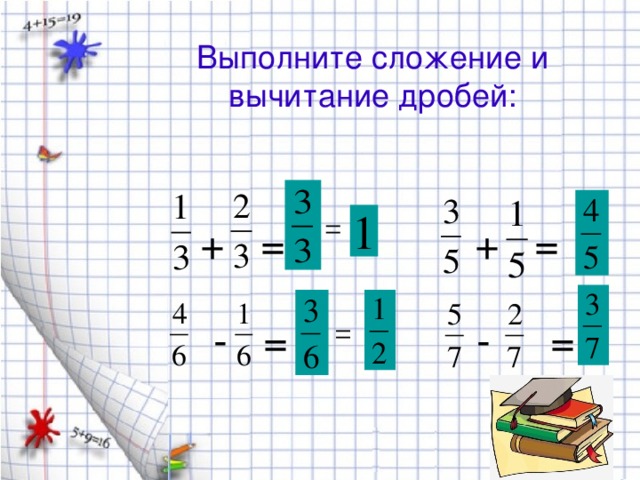
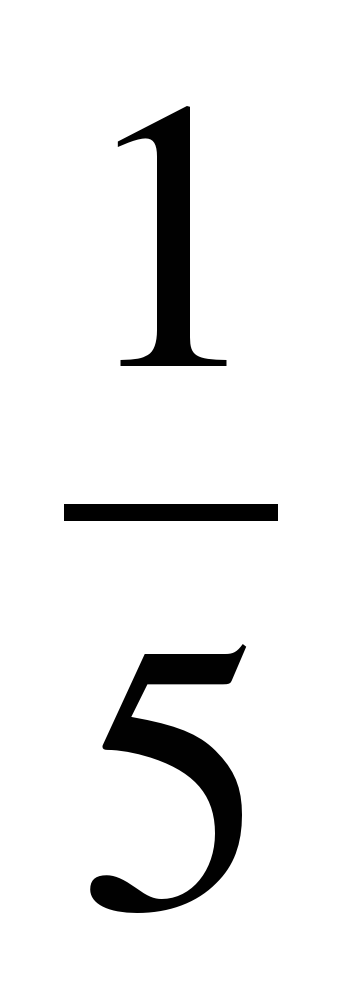
в) Выполните сложение и вычитание дробей:
+ 
; 
- 
; 
+ 
- 
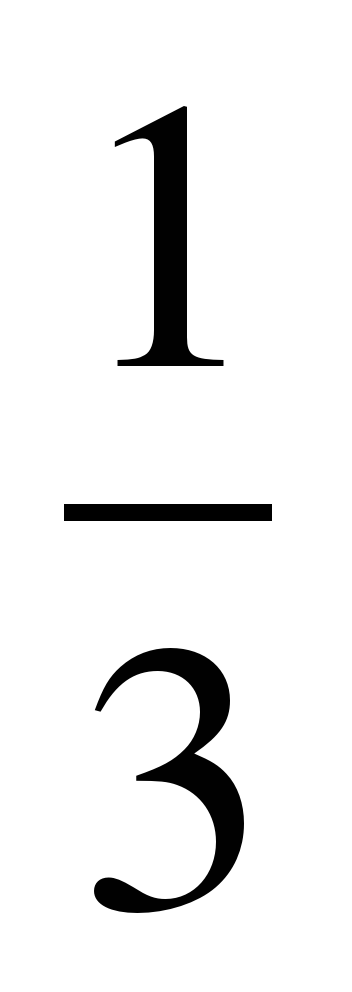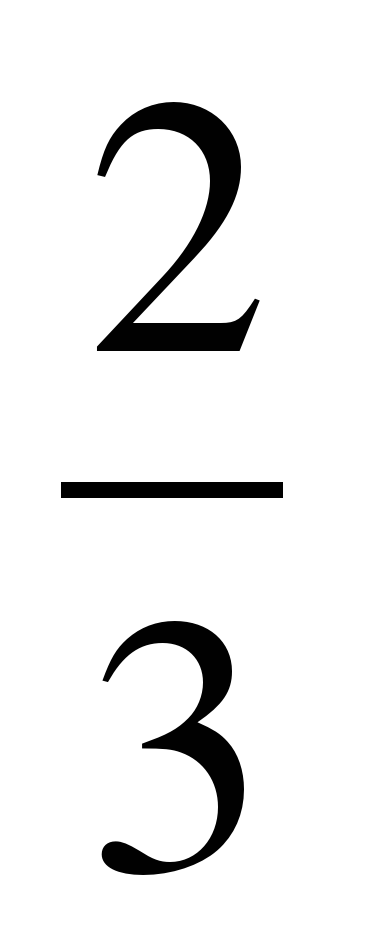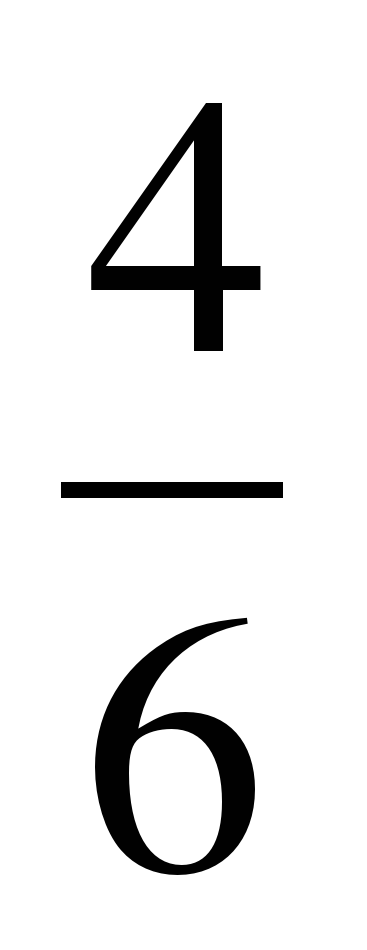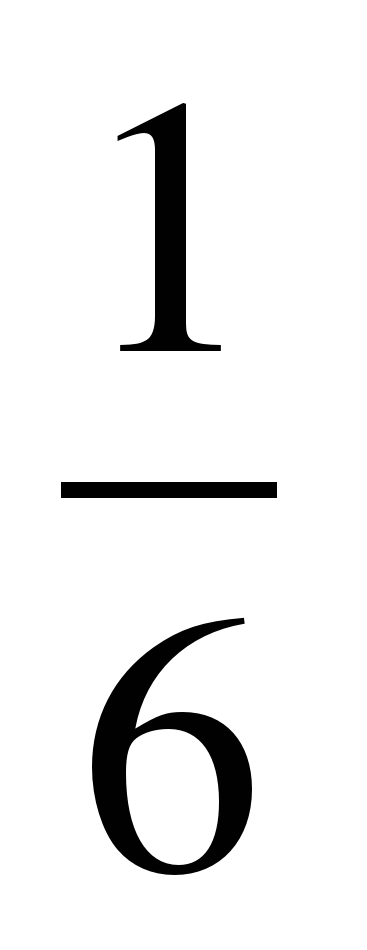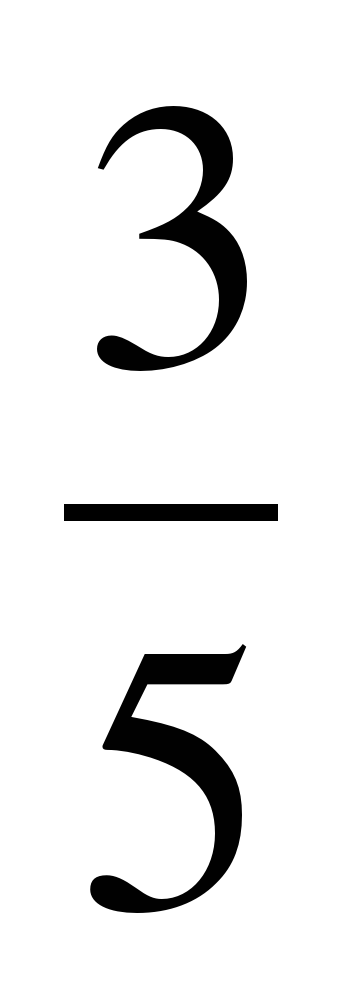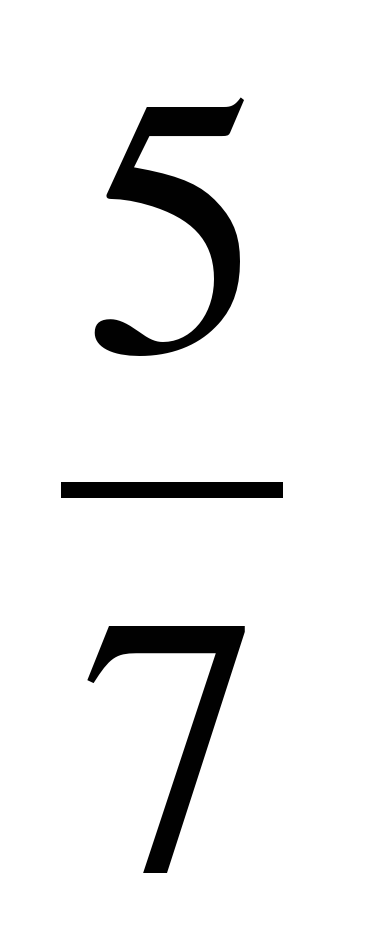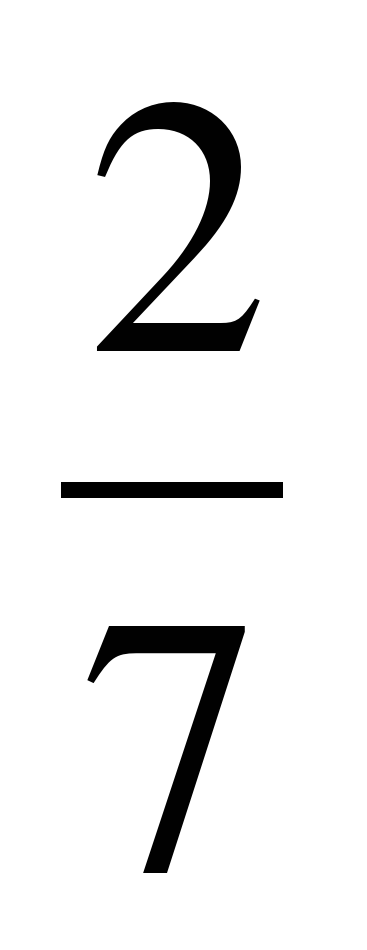
3. Постановка учебной задачи.
(слайд 5)
г) Петя решал задачу 3/10 часа, а примеры - 2/15 часа.
Сколько времени Петя затратил на выполнение математики всего?
РЕШЕНИЕ:
(Учащиеся сразу, отвечая на вопрос задачи, предлагают решение) 3/10 + 2/15 и тут учащимся задается вопрос:
«А умеем ли мы складывать дроби с разными знаменателями?»
«Нет».
Возникла проблема, которая ставится перед учащимися: научиться складывать и вычитать дроби с разными знаменателями.
(слайд 6) Учитель на доске, а учащиеся в тетрадях пишут тему урока.
4. Изучение нового материала, работа с учебником.
Ребята вы уже умеете сравнивать дроби с разными знаменателями. А сегодня мы с вами научимся складывать и вычитать дроби с разными знаменателями.
Откройте учебник на стр. 49 и внимательно прочитайте правило. Затем рассмотрите пример 2 и 3. Объясните решение этих примеров друг другу в парах и запишите в тетрадь.
(слайд 7) А теперь объясните, как решить задачу.
К доске вызывается учащийся для решения задачи, к решению задачи привлекаются так же и другие учащиеся (ответами на вопросы учителя с места)
3/10 + 2/15 = 18/30 + 4/30 = 22/30 = 11/15 (ч.)
Ответ: 11/15 часа.
Итак, как складываются и вычитаются дроби с разными знаменателями?
5. Первичное закрепление.
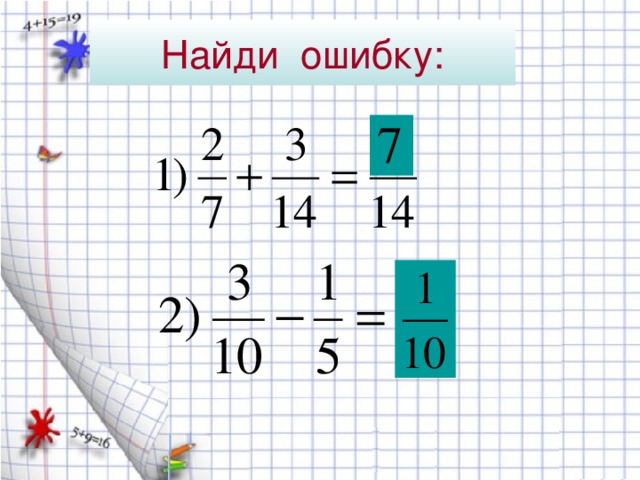
(слайд 8)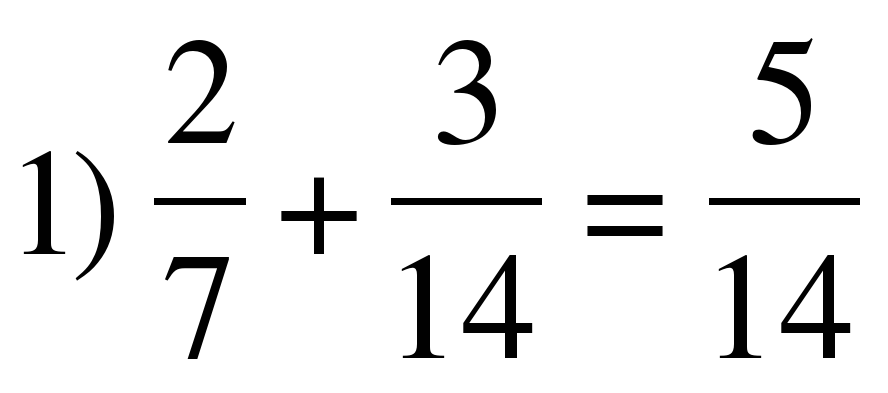
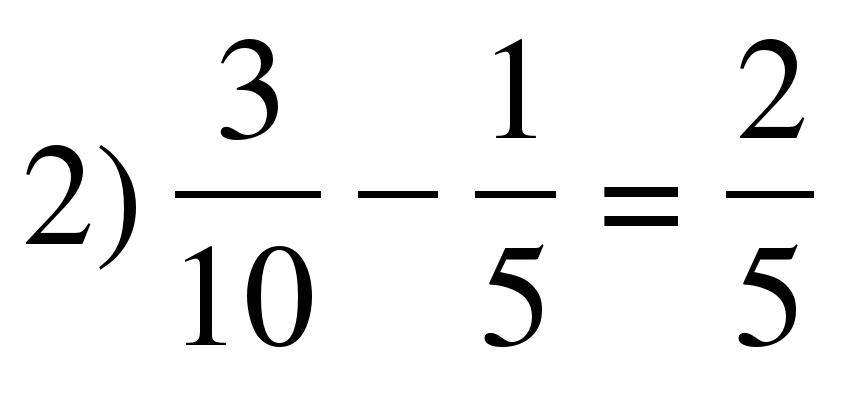
Найдите ошибку
А теперь на стр. 52 прочитайте, как правильно читать сумму и разность дробей.
6. Из истории математики (сообщение учащегося). (слайд 9)
Потребность в более точных измерениях величин привела к тому, что единицы измерения стали делить на несколько равных частей: 2, 4, 8 и т. д. Каждая часть первоначальной мерки получала свое собственное название. Например, половину в Древней Руси называли еш;е полтиной, о четвертой части говорили — ЧЕТЬ, о восьмой части — ПОЛЧЕТЬ, о шестнадцатой части —ПОЛПОЛЧЕТЬ и т. д. Равные части целой мерки называли долями: четвертые доли, восьмые, шестнадцатые и т. д.
Интересная система дробей была в Древнем Риме. Она основывалась на делении древнеримской единицы массы, которая называлась асс.
Запись дробей и алгоритмы действий с ними в древности были так сложны, что учение о дробях считалось самым трудным разделом арифметики. Чтобы его освоить, приходилось заучивать огромное число правил действий с дробями.
Например, в Древнем Риме в ходу было всего 18 различных дробей:
Семис – повинна асса,
Секстанс – шестая его доля.
Сескунция – восьмая,
Триенс – треть асса,
Бес – две трети,
Унция – одна двенадцатая доля,
Семиунция – пол-унция и т.д.
Чтобы работать с долями, надо было твердо знать, что при сложении триенса и секстанта получится семис, а при умножении беса на сескунцию получается унция.
Этих правил было так много, что умение оперировать дробями воспринималось как чудо. Поэтому всегда и везде знание дробей пользовалось особым почетом и уважением.
7. Физкультминутка. (слайд 10)
8. Закрепление.
Работа у доски
№ 319 ( 1 и 3 столбик). Найдите общий признак примеров 1
столбика и 3 столбика.
а)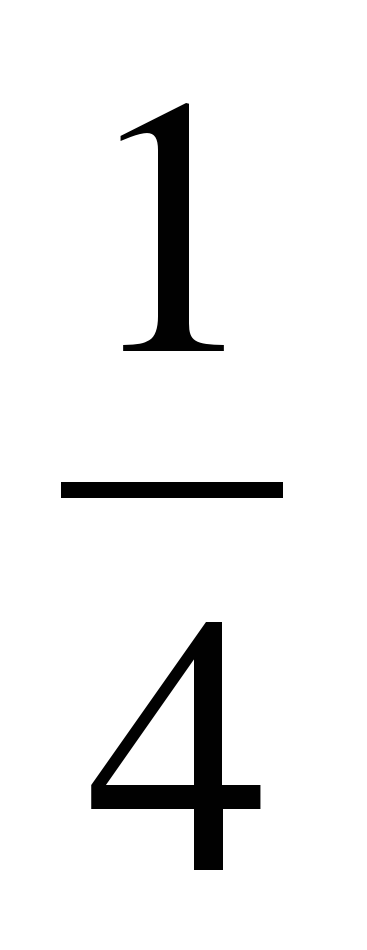 
+ 
= 
+ 
= 
;
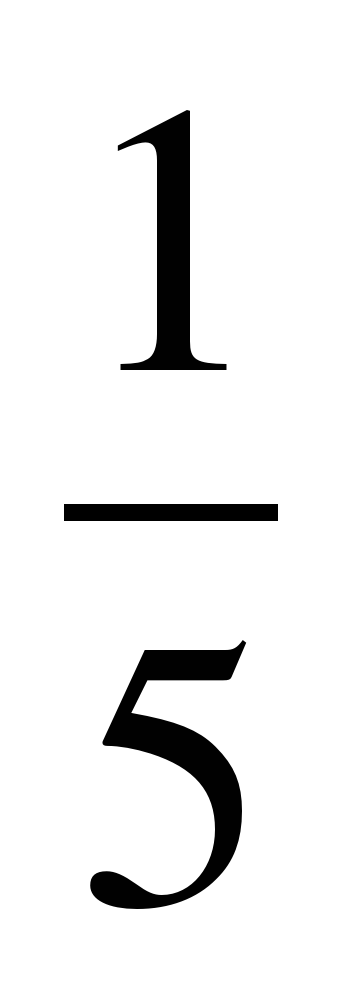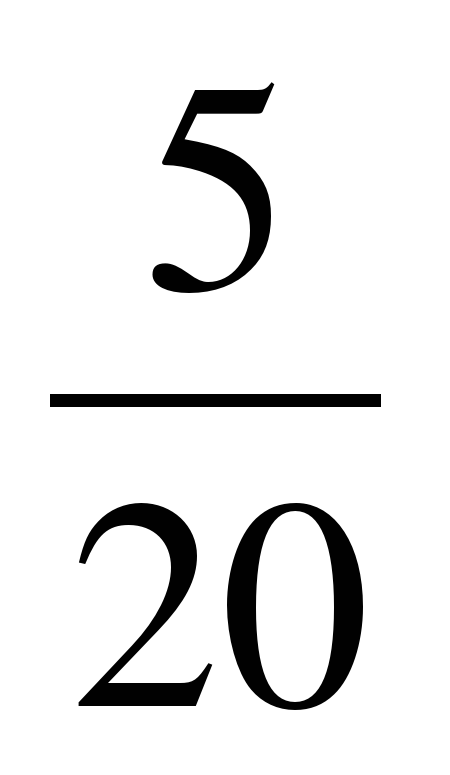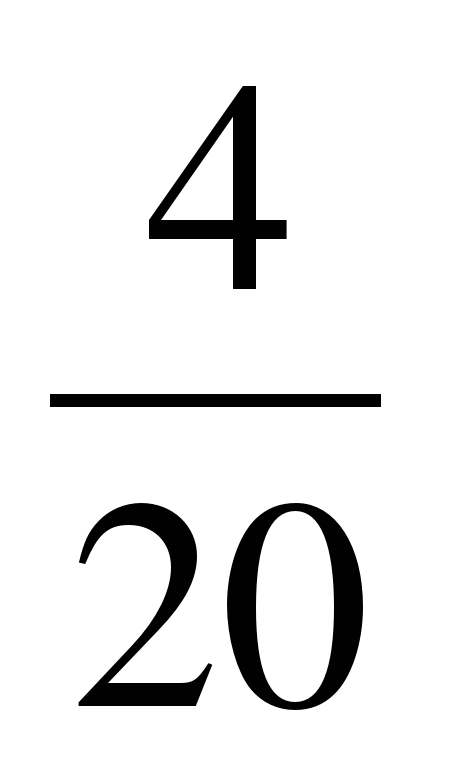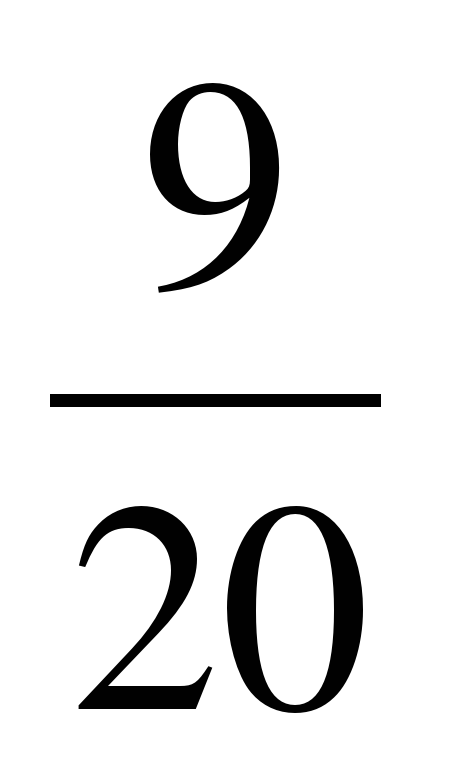б) + 
= 
+ 
= 
;
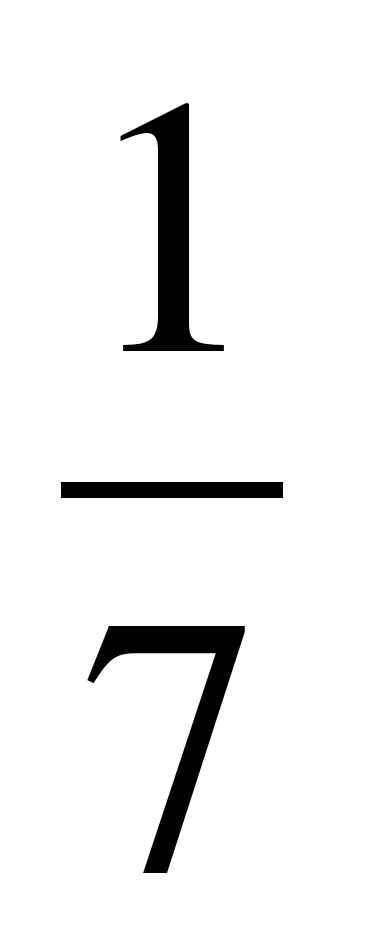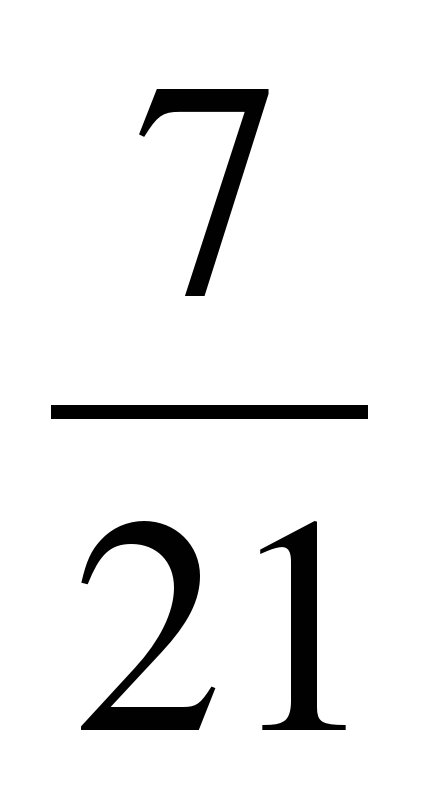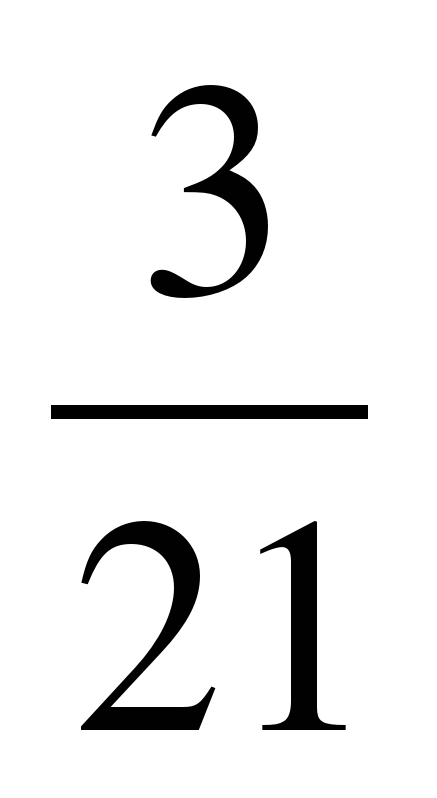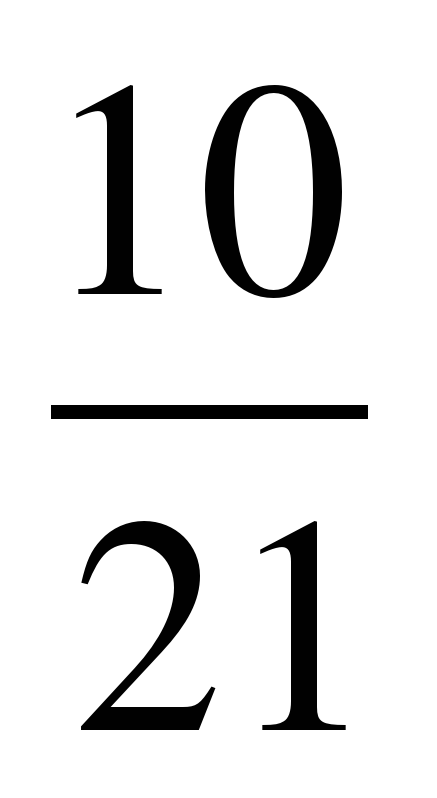в) +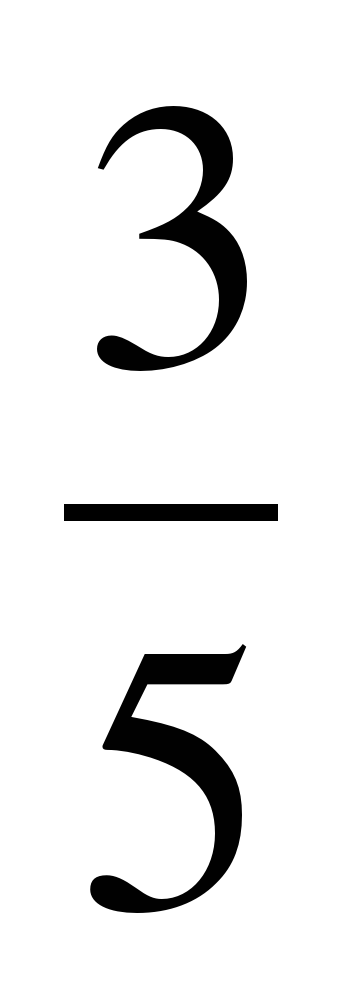 
= 
+ 
= 
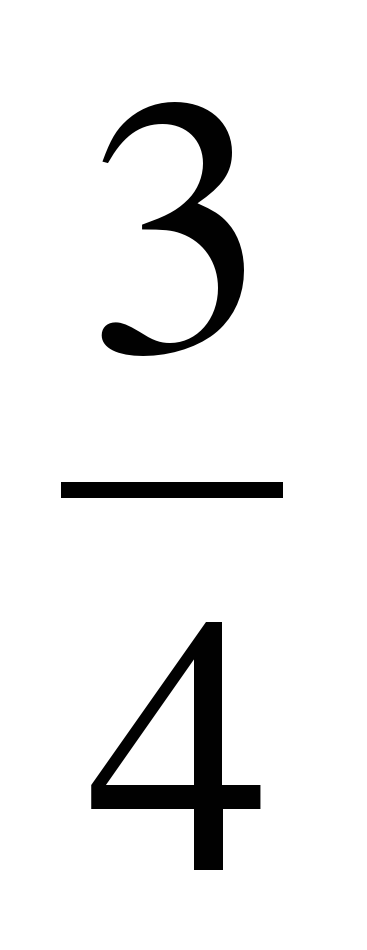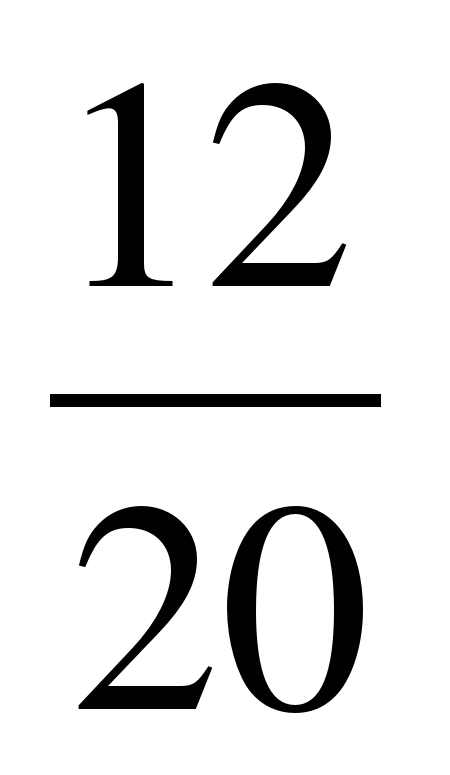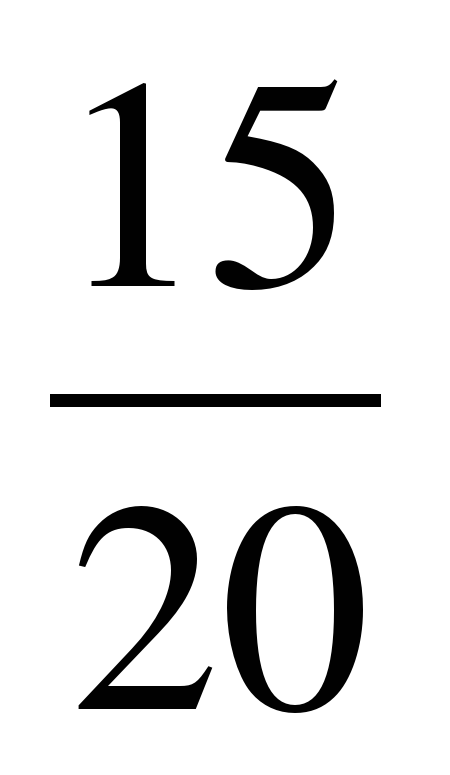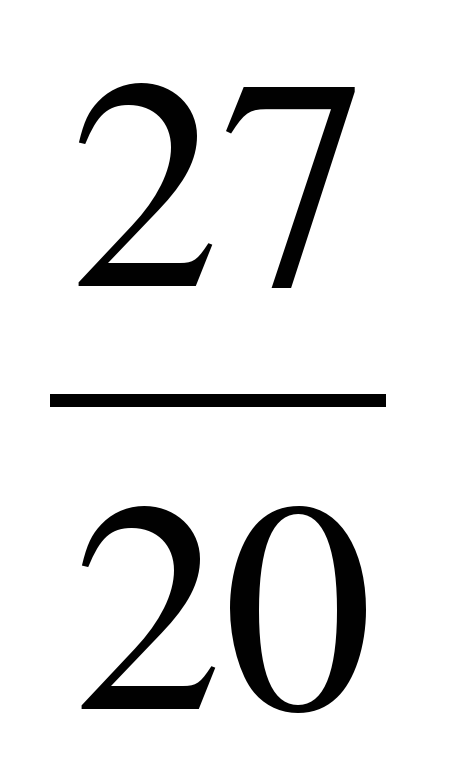= 1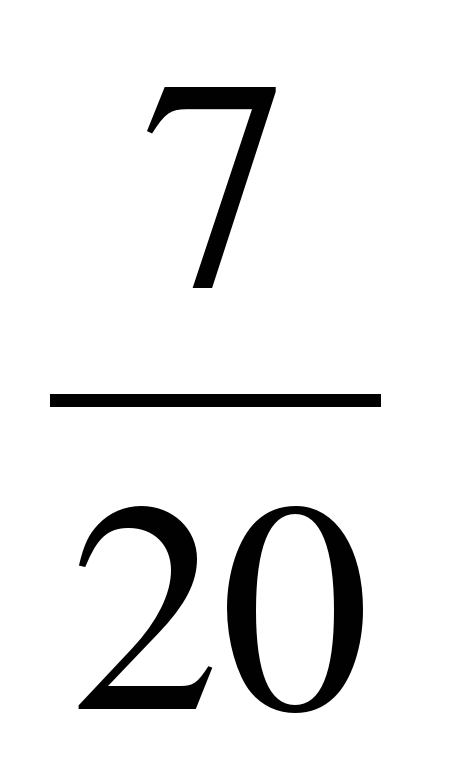
ж)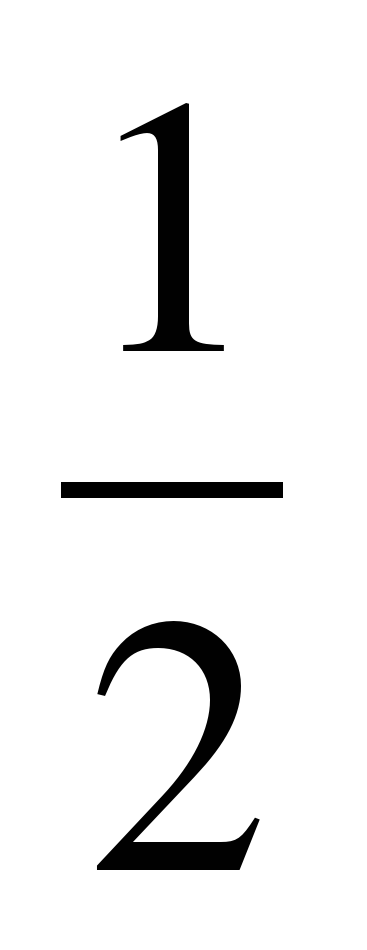 
- = 
- 
= ;
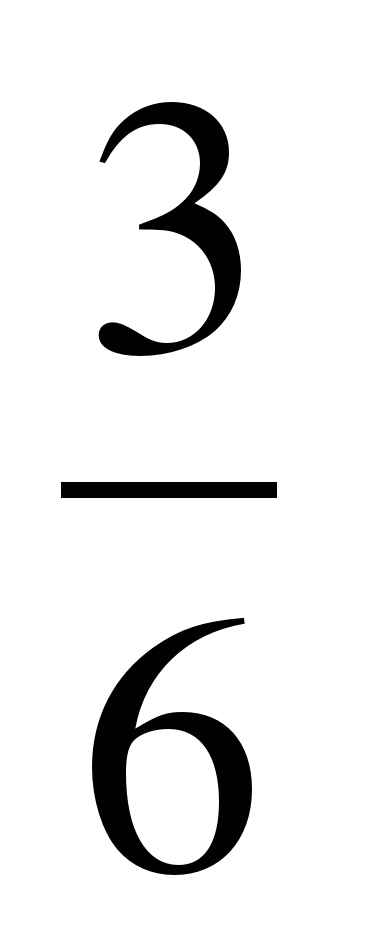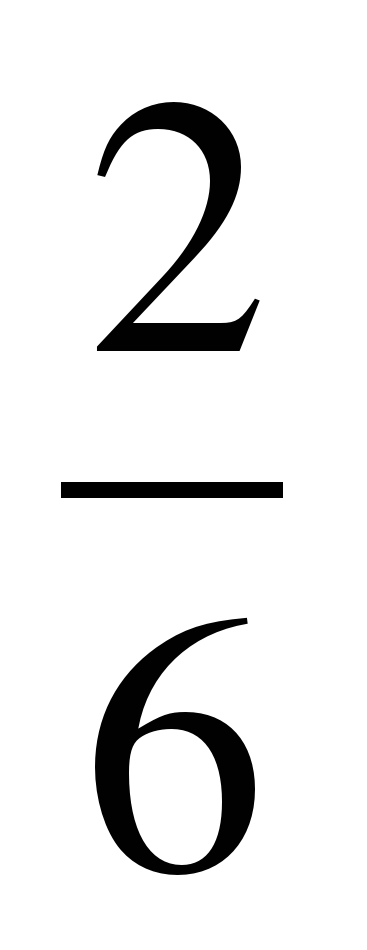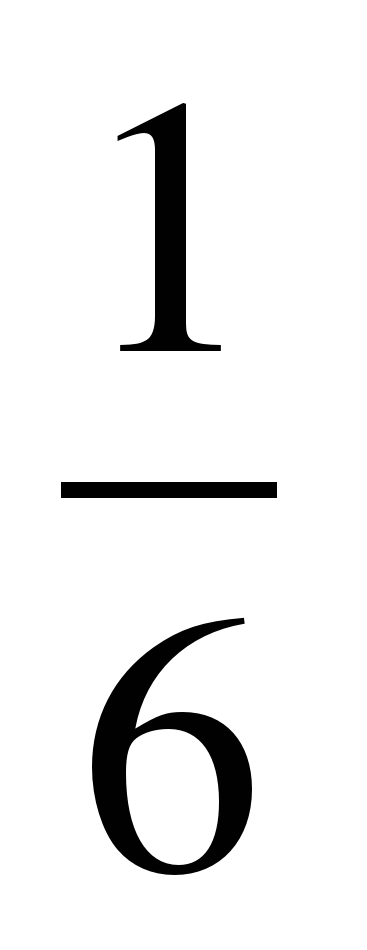з) -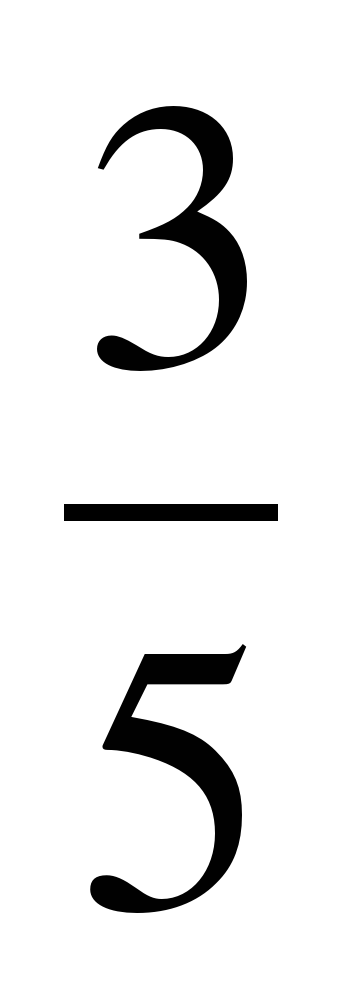 
= 
- 
=
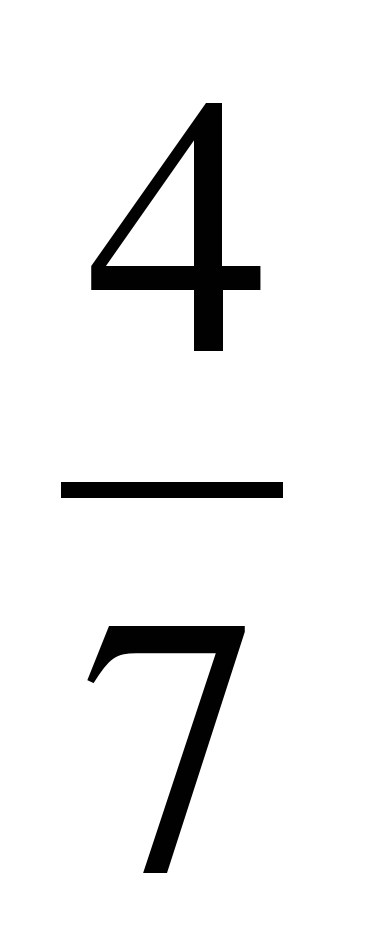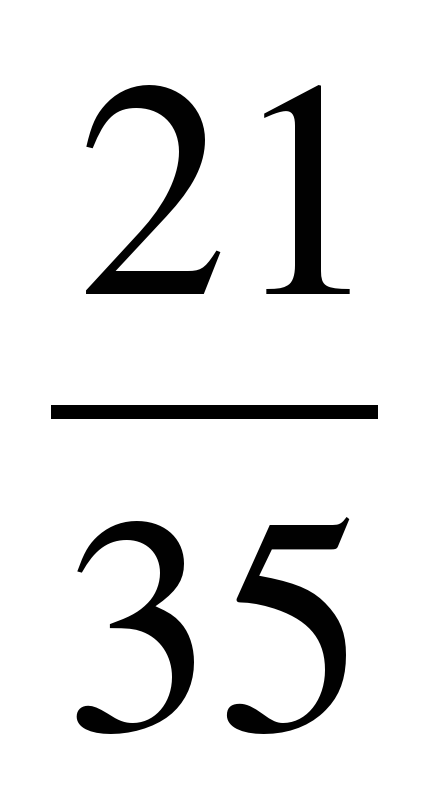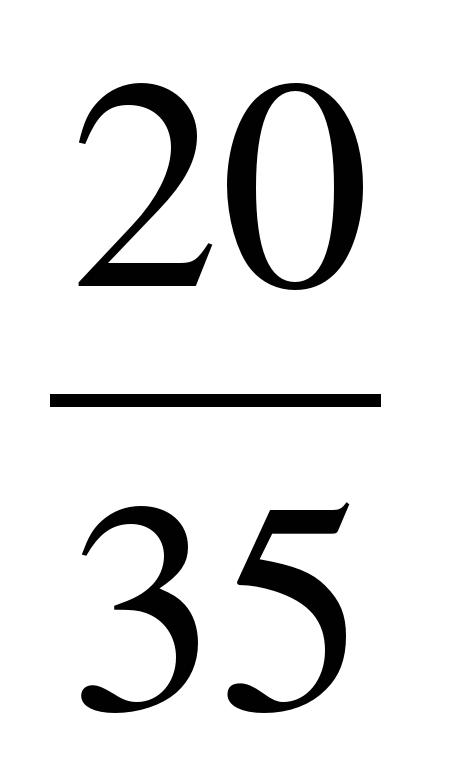и) - = - =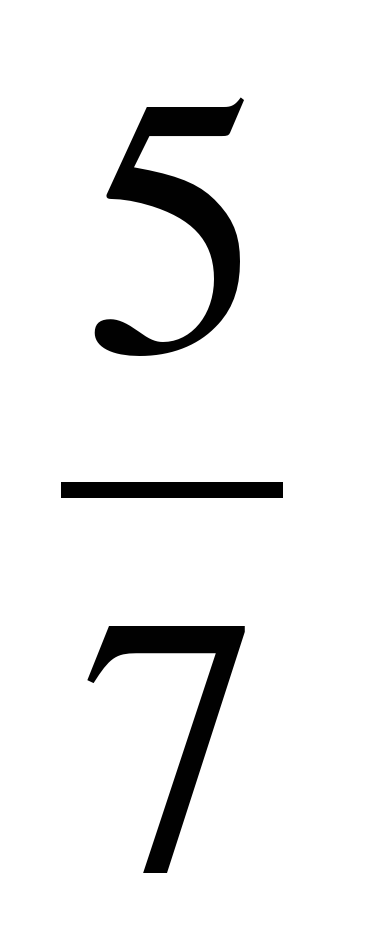
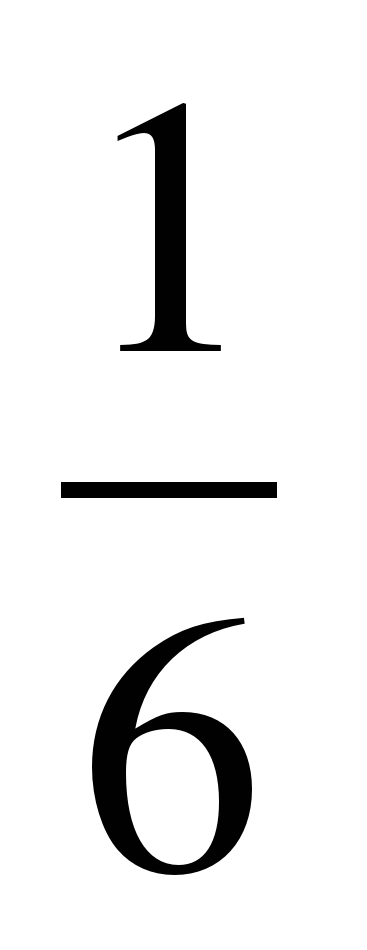№321 ( 1 и 3 столбик). Найдите общий признак примеров 1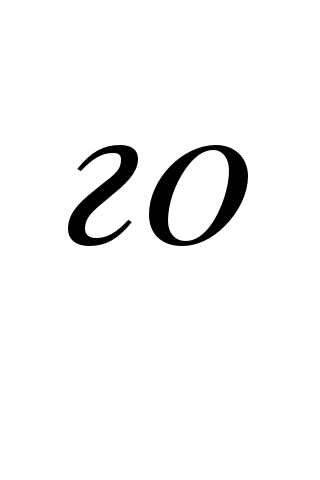 столбика и 3 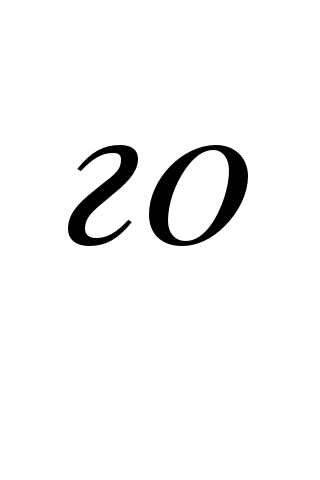столбика.
а) 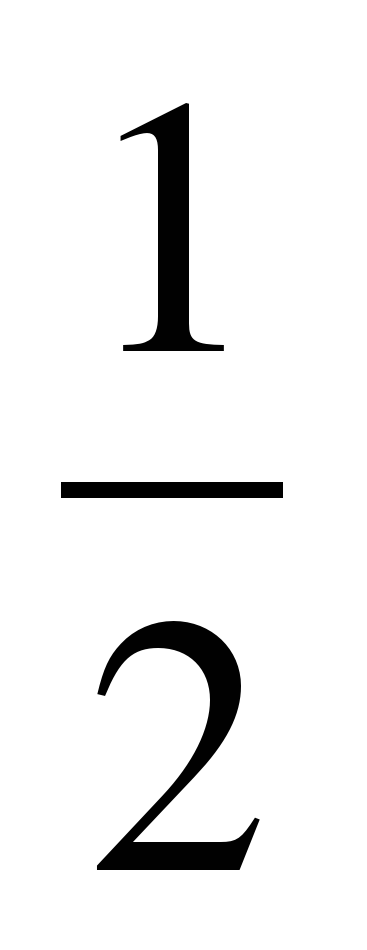+ = + = =1
б) 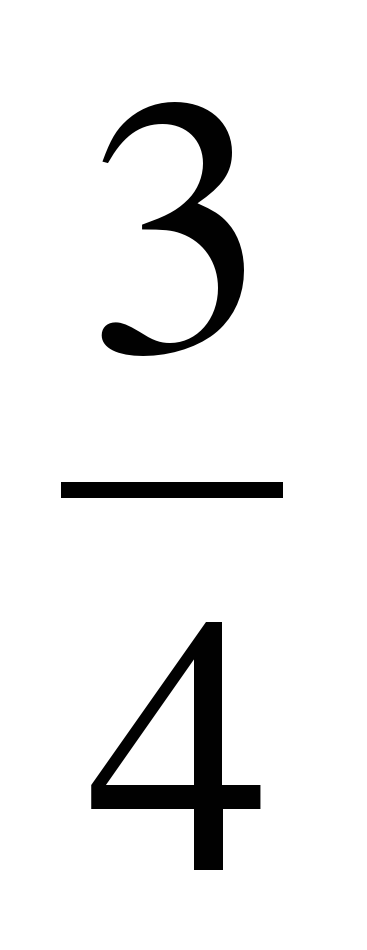- 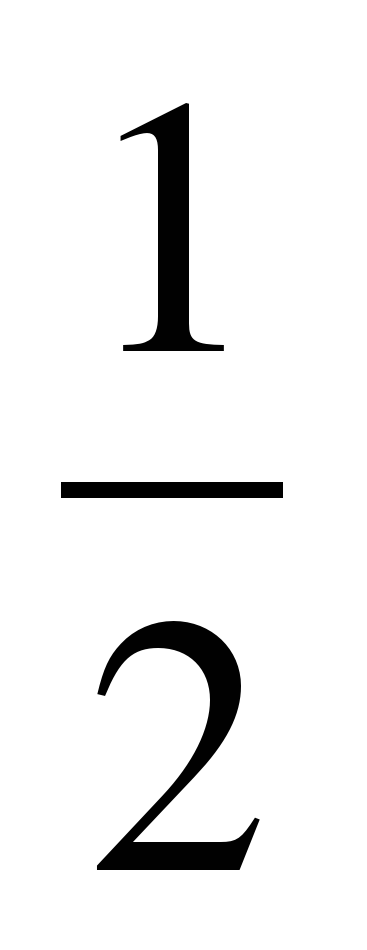= 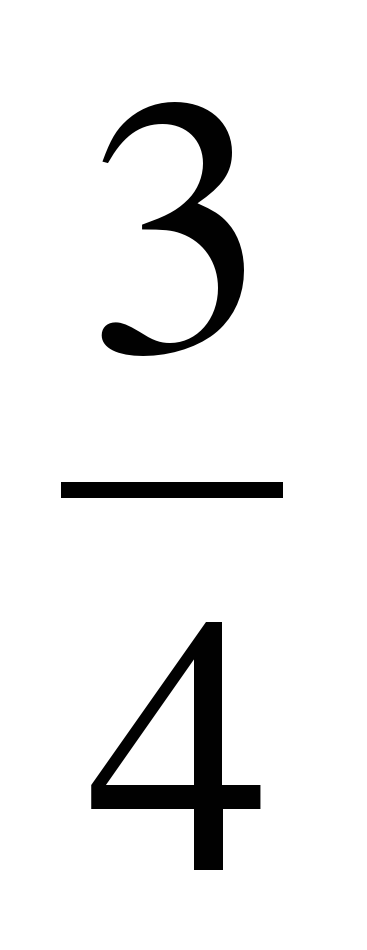+ = = 1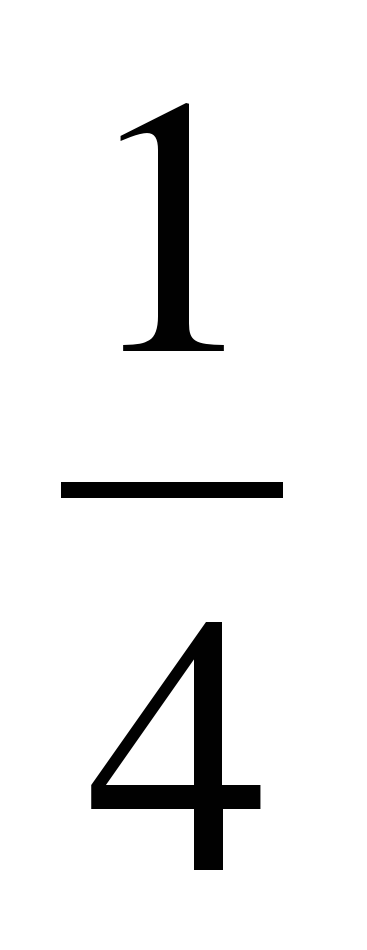
в) - = - =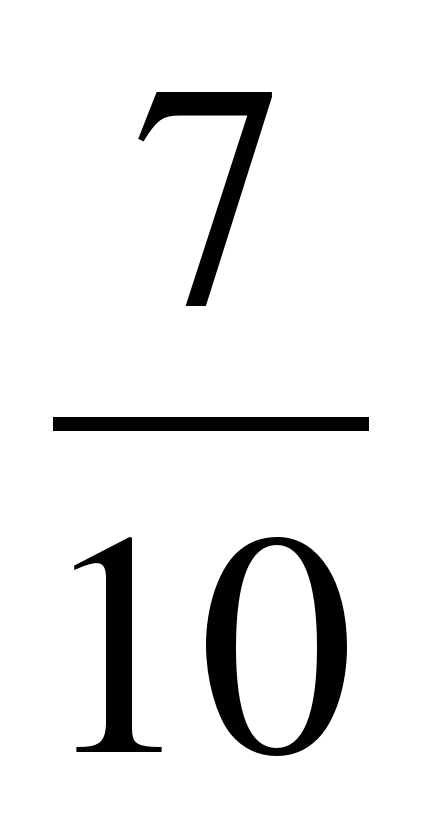
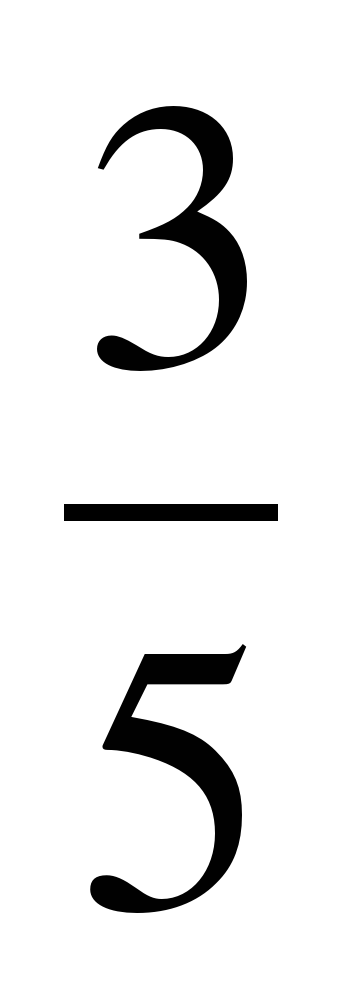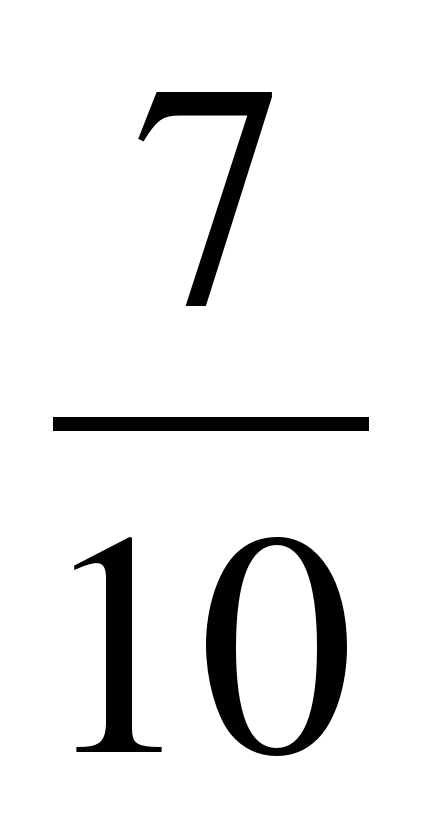ж) + = + = = 1;
з) - = - = =
з) - = - = =
Учащиеся делают вывод.
9. Решение задач на смекалку. (слайд 11) (если времени не останется, то переход на слайд 13)
1) Подставьте вместо треугольников такие числа, чтобы равенства были верными:
-
2) (слайд 12) В примерах вместо звездочек запишите знаки действий «+» или «-» так, чтобы эти равенства были верны:
* * *
10. Рефлексия, выставление оценок.
11. Домашнее задание. (слайд 13)
П.11 (правило) № 360, 361.
Дополнительно № 350.
