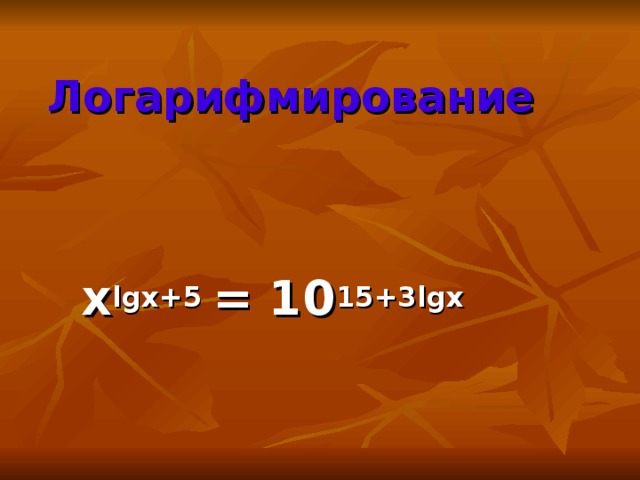Конспект урока "Логарифмические уравнения"

Конспект урока по алгебре и началам анализа

по теме: «Логарифмические уравнения»

Учитель: Щёкина Н.А.

Пояснительная записка

Планирование курса алгебры и начал анализа для учащихся 11 класса составлено на основе:

• «Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений/ А.Н.Колмогоров, Ю.П.Дудницын и др.; под ред. А.Н.Колмогорова. – М.: Просвещение, 2008.

• Профильное обучение: тематическое планирование по математике для 10-11 кл.: пособие для учителя/ сост. Т.А.Бурмистрова. – М.: Просвещение, 2006.

• Примерные программы по математике/ сост. Э.Д.Днепров, А.Г.Аркадьев. – М.: 2007.

Данный урок из раздела «Показательные и логарифмические уравнения».

Показательные и логарифмические уравнения:

1. Показательная функция – 2

2. Показательные уравнения, системы уравнений и неравенств – 4

Контрольная работа № 4 – 1

1. Логарифмы и их свойства – 3

2. Логарифмическая функция. Понятие об обратной функции – 2

3. Решение логарифмических уравнений и неравенств – 5

Контрольная работа №5 – 1

Это третий урок из 5-ти в теме «Логарифмические уравнения и неравенства».

Урок комплексного применения ЗУН по теме «Логарифмические уравнения».

Данный урок предназначен для учащихся 11 класса общеобразовательной школы, имеющих средний уровень обучения.

Результативность урока:

• учащиеся знают и умеют применять определение логарифма, свойства логарифмов, формулу перехода;

• учащиеся умеют находить значение логарифма и проводить преобразования выражений, содержащих логарифмы;

• учащиеся определяют методы решения логарифмических уравнений и умеют их решать;

• учащиеся умеют использовать компьютерные технологии для самостоятельной работы.

Тема урока: Логарифмические уравнения.

Цель урока: закрепление знаний и умений по решению

логарифмических уравнений.

Задачи:

1. Учебные задачи:

- умение применять полученные теоретические знания для решения заданий;

- умение использовать компьютерные технологии для самостоятельной работы.

1. Развивающие задачи:

- развитие мышления учащихся, коммуникативных способностей;

- формирование навыков умственного труда: поиск рациональных путей решения, самообразование.

1. Воспитательные задачи:

- воспитание познавательной активности, ответственности.

Оборудование:

• учебник для 10-11 кл общеобразовательных учреждений «Алгебра и начала анализа» под редакцией А.Н.Колмогорова,

• диск «Математика. 5- 11 классы» («Дрофа»),

• диск «Уроки алгебры Кирилла и Мефодия. 10-11 классы»,

• таблица ответов для МД,

• лист самоконтроля,

• лист с Домашним Заданием,

• мультимедийный проектор,

• презентация 1 «Логарифмические уравнения»,

• презентация 2 «Логарифм и его свойства»,

• презентация 3 «Математический диктант»,

• презентация 4 «Примеры уравнений».

Конспект урока по алгебре и началам анализа для учащихся 11 кл.

План урока:

1. Организационный момент (2 мин).

2. Проверка домашнего задания. Устный опрос (8 мин).

3. Математический диктант (4 мин).

4. Практическая часть (8-10 мин).

5. Самостоятельная работа (8-10 мин).

6. Задание на дом (3 мин).

7. Итоги урока (5 мин).

Ход урока:

1. Организационный момент:

• постановка цели и задач (презентация 1,приложение 1,слайд 1-3):

слайд 1 – Тема урока;

слайд 2 – Цель урока;

слайд 3 – Задачи урока.

1. а) Проверка домашнего задания:

№ 514(а); 518 (а) – устно (решение на доске);

№522 (а); №530 (г) – у доски выполняют 2 ученика.

№ 514(а). Решите уравнение:

log_½ (2x – 4) = -2 (определение логарифма).

Ответ: 4.

№ 518(а). Решите уравнение:

log_a x = 2log_a 3 + log_a 5 (свойства логарифмов).

Ответ: 45.

№ 522(а). Решите уравнение:

1 : (lg x + 1) + 6 : (lg x + 5) = 1.

Ответ: 0, 01 и 1000.

№ 530(г). Решите систему уравнений:

lg x – lg y = lg 15 – 1,

10 ^{lg(3x + 2y)} = 39.

Ответ: (9;6).

II. б) Устный опрос.

Повторение ранее изученных теоретических знаний:

1. Определение логарифмического уравнения. Методы решения логарифмических уравнений (презентация1,приложение1,слайд 4-6).

Учитель. Какое уравнение называется логарифмическим уравнением?

Слайд 4. Определение: Логарифмическим уравнением называется уравнение, содержащее переменную под знаком логарифма и/ или в основании логарифма.

Учитель (слайд 5).

Для успешного решения логарифмических уравнений Вам необходимо:

• Безошибочно решать простейшее логарифмическое уравнение.

• Не только знать все логарифмические тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать лишних корней, а тем более – не терять решения уравнения.

• Четко, подробно и без ошибок проделывать математические преобразования уравнений. Это называется математической культурой. При этом сами выкладки должны делаться автоматически руками, а голова должна думать об общей путеводной нити решения.

• Знать методы решения задач. Для правильного ориентирования на каждом этапе вам придется (сознательно или интуитивно!):

• Определить тип уравнения;

• Вспомнить соответствующий этому типу метод решения задачи.

Учитель. Какие методы решения логарифмических уравнений вы знаете?

Слайд 6. Методы решения уравнения:

• Уравнения, решаемые по определению логарифма.

• Уравнения, решаемые приведением к квадратному уравнению.

• Потенцирование.

• Логарифмирование.

• Уравнения, решаемые приведением к одному основанию.

• Графический метод решений.

2. Определение логарифма. Свойства логарифмов (презентация 2, приложение 2, слайд 1-3).

Учитель. При решении логарифмических уравнений необходимо знание определения логарифма и его свойств.

? - Сформулируйте определение логарифма.

? – При каких условиях эта формула имеет смысл?

Слайд 1. Определение логарифма:

• Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести основание а, чтобы получить число b.

log_ab = x, a^х = b, где b0, a0, a ≠ 1.

? – Какие свойства логарифмов вы знаете?

Слайд 2. Свойства логарифмов:

1. log_а 1 = 0.

2. log_a а= 1.

3. log_a(ху) = log_a х + log_a у.

4. log_a(х/у) = log_a х – log_a у.

5. log_a(х^р) = р log_a х.

Учитель. При решении логарифмических уравнений иногда нам необходимо перейти к другому основанию логарифма, для этого используется формула перехода логарифма.

? – Расскажите, как же перейти к другому основанию у логарифма. Запишите формулу перехода.

Слайд 3. Формула перехода:

log _b x

log _a x = _________

log _b a

III. Математический диктант.

Использование заданий из тренировочных материалов

Единого Государственного Экзамена (презентация 3,

приложение 3, слайд 1-9).

Учитель. Сейчас мы с вами проведем математический диктант. В математическом диктанте использованы задания, взятые из тренировочных материалов Единого Государственного Экзамена.

Взяли в руки ручку и таблицу для ответов к математическому диктанту (приложение 5). Итак, приготовились, начали. (Каждое задание - 25 с)

Слайд 1. Математический диктант.

Слайд 2.

1. Упростите выражение log₃ 54 + log₃ (1/2).

Ответы: 1) 27, 2) 2, 3) 3, 4) 9.

Слайд 3.

2. Вычислите log₁₂ (7/ 144) – log₁₂ 7.

Ответы: 1) 1, 2) 2, 3) -1, 4) -2.

Слайд 4.

3. Найдите значение выражения - 4 log₆ (6³).

Ответы: 1) 3, 2) -12, 3) -64, 4) -1.

Слайд 5.

4. Вычислите 10^{lg 9} – 14.

Ответы: 1) -5, 2) 23, 3) -4, 4) 5.

Слайд 6.

5. Упростите log_1/5 (1/10) + log_1/5 250.

Ответы: 1) 25, 2) 2, 3) 5, 4) -2.

Слайд 7.

6. Вычислите log₂ 50 – 2 log₂ 5.

Ответы: 1) 20, 2) 1, 3) log₂ 30, 4) 8log₂ 5.

Слайд 8.

7. Решите уравнение и запишите ответ: log₅ x = log₅ 6 + log₅ 3 .

Слайд 9.

8. Решите уравнение и запишите ответ: log₄ x + log₄ 3 = log₄ 15.

№1	№2	№3	№4	№5	№6	№7	№8
3	4	2	1	4	2	18	5

Таблица

ответов:

Критерии оценивания МД:

• оценка «5» - за верно выполненные 8 заданий;

• оценка «4» - за верно выполненные 6-7 заданий;

• оценка «3» - за верно выполненные 4-5 заданий;

• оценка «2» - за выполнение менее 4 заданий.

IV. Практическая часть

Решение заданий у доски и в тетрадях, с последующей проверкой и комментариями (3 учащихся у доски, с обратной стороны).

1 группа - № 520 (в); 529 (а) – группа «3»/ «4»;

2 группа - № 529(а); № 523(г) – группа «4»/ «5».

Дополнительное задание № 519(а) или №524(а).

1 группа. № 520(в). Решите уравнение: log₅² x – log₅ x = 2.

Ответ: 0,2 и 25.

№ 529(а). Решите систему уравнений: log_⅓ (x + y) = 2,

log₃ (x – y) = 2.

Ответ: (4 5/9; -4 4/9).

2 группа. № 529(а). Решите систему уравнений: log_⅓ (x + y) = 2,

log₃ (x – y) = 2.

Ответ: (4 5/9; -4 4/9).

№ 523(г). Решите уравнение: log₂₅ x + log₅ x = log_1/5 √8.

Ответ: ½.

Дополнительное задание:

• № 519(г). Решите уравнение: log₅ (x² + 8) – log₅ (x + 1) = 3log₅ 2.

Ответ: 0 и 8.

• № 524(а). Решите уравнение: log₂ (9 – 2^x) = 3 – x.

Ответ: 0 и 3.

V. Самостоятельная работа на компьютере.

Заполнение листа самоконтроля (приложение 5). Задание у каждого учащегося записано на карточке.

1) Диск «Математика. 5-11 классы»

• Пункт 3.3. Логарифмы. Свойства логарифмов. №1, №5.

• Пункт 3.5. Показательные и логарифмические уравнения.

№2 (а; б) - логарифмические уравнения.

2) Диск «Уроки алгебры Кирилла и Мефодия. 10-11 кл.».

• У-16. Логарифмы. Седьмое действие над числами (итоговое тестирование).

• У-17. Логарифм произведения, частного, степени (дополнительное тестирование).

3) Дополнительное задание №523 (б) из учебника.

№ 523(в). Решите уравнение: log₃ х – 2log_1/3 х = 6.

Ответ: 9.

VI. Задание на дом:

Карточка (приложение 5).

1. Задания ЕГЭ повышенной сложности (В).

1. Найдите корень (или сумму корней, если их несколько) уравнения:

log₆ (3x+88) – log₆ 11 = log₆ x.

1. Найдите сумму корней уравнения:

log²₄ (x-3) = log₄ (x-3) + 2.

1. Найдите произведение корней уравнения:

⁴√12 + 4x – x² * lg (31 - x - x² ) = 0.

1. Учебник А. Н. Колмогорова «Алгебра и начала анализа.10-11 кл»

п. 37-39, №529(в, г).

Учитель. Как, каким способом вы будете решать эти уравнения?

VII. Итоги урока:

• заполнение листа самоконтроля и выставление оценок;

• беседа с учащимися о пробелах в знаниях, рекомендации учителя.

Учитель. А сейчас, мы еще раз вспомним – что же такое логарифмическое уравнение и какими способами (методами) оно решается. Посмотрим на примеры уравнений, решаемых разными методами (презентация 4, приложение 4, слайд 1-8).

Слайд 1. Определение логарифмического уравнения.

Слайд 2. Методы решения уравнений.

Слайд 3. Уравнения, решаемые по определению логарифма:

log_0,3 (5 + 2x) = 1.

Слайд 4. Уравнения, решаемые приведением к квадратному уравнению:

lg² x – lg x + 1 = 0.

Слайд 5. Потенцирование:

log₂ (x + 15) = log₂ (x + 1).

Слайд 6. Логарифмирование:

x^lgx+5 = 10^15+3lgx.

Слайд 7. Уравнения, решаемые приведением к одному основанию:

log₂₅x+log₅x=log_0.2√8.

Слайд 8. Графический метод решения:

log₃ x = 0,5x – 0,5.

ПРИЛОЖЕНИЕ 5.

Лист самоконтроля учени__ 11 класса __________________________________

	Д/З	Устн опрос	Пракчасть	Мат Дикт.	Тесты по алгебре КиМ		Математика 5-11 кл Дрофа			Итог уч-ся	Итог Уч-ля
Задание					У-16 ИтогТ	У-17 Доп.Т	П.3.3 №1	П.3.3 №5	П.3.5 №2а;б
Оценка о выпол-нении

Таблица ответов для МД учени__ 11 класса _________________________

№ 1	№2	№3	№4	№5	№6	№7	№8	Оценка

Задание на дом

1. Задания ЕГЭ повышенной сложности (В).

1. Найдите корень (или сумму корней, если их несколько) уравнения:

log₆ (3x+88) – log₆ 11 = log₆ x.

1. Найдите сумму корней уравнения:

log²₄ (x-3) = log₄ (x-3) + 2.

1. Найдите произведение корней уравнения:

__________

⁴√12 + 4x – x² * lg (31 - x - x² ) = 0.

1. Учебник п. 37-39, №529(в,г).

10

0, a0, a ≠ 1." width="640"

Логарифм

• Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести основание а , чтобы получить число b .

log a b = x,

a x = b, где b0, a0, a ≠ 1.

Свойства логарифмов

• log a а= 1.
• log a 1 = 0.
• log a (ху) = log a х + log a у.
• log a (х/у) = log a х – log a у.
• log a ( х р ) = р log a х

Формула перехода: log b x log a x = _________ log b a

Логарифмические уравнения

Цель:

• Закрепление знаний и умений по решению логарифмических уравнений .

Задачи

Учебные задачи:

• Умение применять полученные теоретические знания для решения заданий;
• Умение использовать компьютерные технологии для самостоятельной работы.

Развивающие задачи:

• Развитие мышления учащихся, коммуникативных способностей;
• Формирование навыков умственного труда: поиск рациональных путей решения, самообразование.

Воспитательные задачи:

• Воспитание познавательной активности, ответственности.

Логарифмическое уравнение -

• это уравнение, содержащее переменную под знаком логарифма и/или в основании логарифма.

Для успешного решения логарифмических уравнений необходимо:

• Безошибочно решать простейшие логарифмические уравнения.
• Знать все логарифмические тождества, находить множества значений переменной, на которых эти тождества определены.
• Выполнять математические преобразования уравнений.
• Знать методы решения задач.

Методы решения логарифмических уравнений

• Уравнения, решаемые по определению логарифма.
• Уравнения, решаемые приведением к квадратному уравнению.
• Потенцирование.
• Логарифмирование.
• Уравнения, решаемые приведением к одному основанию.
• Графический метод решений.

Математический диктант

1. Упростите выражение log 3 54 + log 3 (1/2)

• 27

• 3

• 2

• 9

2 . Вычислите log 12 (7/ 144) – log 12 7

• 1

• - 1

• 2

• - 2

3 . Найдите значение выражения - 4 log 6 (6 3 )

• 3 -4

• - 12

• - 64

• - 1

4. Вычислите 10 lg9 - 14

• - 5

• - 4

• 23

• 5

5 . Упростите log 1/5 (1/10) + log 1/5 250

• 25

• 2

• 5

• -2

6. Вычислите log 2 50 – 2 log 2 5

• 20

• log 2 30

• 8 log 2 5

• 1

7. Решите уравнение

log 5 x = log 5 6 + log 5 3

8. Решите уравнение

log 4 x + log 4 3 = log 4 15

Логарифмическое уравнение -

• это уравнение, содержащее переменную под знаком логарифма и/или в основании логарифма.

Методы решения уравнений

• Уравнения, решаемые по определению логарифма.
• Уравнения, решаемые приведением к квадратному уравнению.
• Потенцирование.
• Логарифмирование.
• Уравнения, решаемые приведением к одному основанию.
• Графический метод решений.

Уравнения, решаемые по определению логарифма.

log 0,3 (5 + 2x) = 1

Уравнения, решаемые приведением к квадратному уравнению.

lg 2 x – lg x + 1 = 0

Потенцирование

log 2 (x + 15) = log 2 (x + 1)

Логарифмирование

x lgx+5 = 10 15+3lgx

Уравнения, решаемые приведением к одному основанию.

log 25 x+log 5 x=log 0.2 √8

Графический метод решения

log 3 x = 0,5x – 0,5