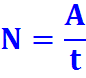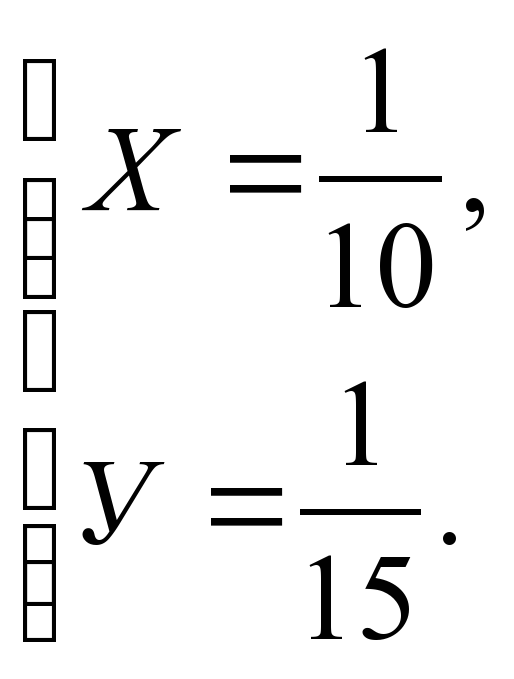Конспек урока математики

Цели урока: 1. Развитие прочных навыков решения задач данных типов; 2. Систематизация понятия системы уравнений с двумя переменными, ее решения; 3. Воспитание познавательного интереса к предмету. Задачи урока:1. Развивать основные умения решения задач по основному алгоритму; 2. Развивать внимание, логическое мышление; 3. Закреплять и расширять умение применять полученные знания к решению прикладных задач. Оборудование:1.Презентация к уроку. 2.Раздаточные материалы для учащихся. 3. Карточки для рефлексии. Ход урока: Терпенье и труд все перетрут. 1. Орг. момент Добрый день! Добрый час! Как я рада видеть вас. Прозвенел уже звонок Начинается урок. Улыбнулись. Подровнялись. Друг на друга поглядели И тихонько дружно сели. 2. Мотивация урока. Сегодняшний урок я хотела начать с загадки немецкого теоретика культуры, литературной критики, переводчика, философа и эссеиста Беньямина Вальтера(1892 - 1940): Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и краткое, самое дорогое, но и дёшево ценимое нами? (время). Итак, у нас всего 45 минут и мне очень хотелось бы, чтобы это время пролетело для вас незаметно и с пользой. 3. Актуализация опорных знаний. Объявление темы, цели и задач урока. В тетрадях написали число, классная работа и тему урока. Текстовые задачи представляют собой раздел математики, традиционно предлагаемый на государственной аттестации по математике. Они вызывают трудности у многих учащихся. Типы задач: • Задачи на движение двух тел. • Задачи на работу. • Задачи на проценты. • Задачи на смеси, сплавы, растворы. Устное решение задач: а) Недалеко от берега стоит корабль со спущенной на воду верёвочной лестницей вдоль борта. У лестницы 10 ступенек. Расстояние между ступеньками 30 см. Самая нижняя ступенька касается поверхности воды. Океан сегодня спокоен, но начинается прилив, который поднимает воду за каждый час на 15 см. Через сколько времени покроется водой третья ступенька верёвочной лестницы. Пояснение: вода никогда не покроет третью ступеньку, потому что с водой поднимается и корабль, и веревочная лестница. Подготовительная работа 1) Бассейн можно наполнить за 3 ч. Какая часть бассейна наполняется за 1 ч? 2. Бассейн наполняется за 10 ч. Какая часть бассейна наполнится за 1 ч? За 4 ч? 3) В каждый час наполняется бассейна. За сколько часов наполнится бассейн? 4) В каждый час труба наполняет бассейна. За сколько часов она наполнит бассейн? 4. Решение задач на совместную работу. Указания к задачам на совместную работу. Основными компонентами этого типа задач являются: а) Объём, выполняемой работы (А); б) Время работы (t); в) Производительность труда (работа, выполненная в единицу времени-N). Задачи с одной переменной. Задача 1. Мастер, работая самостоятельно, может изготовить партию из 200 деталей за некоторое время. Ученик за это же время может изготовить только половину всех деталей. Работая вместе, они могут изготовить всю партию деталей за 4 ч. За какое время мастер может изготовить все детали, работая самостоятельно? Задача 2. Саша и Маша решают задачи. Саша может решить 20 задач за то время, за которое Маша может решить в 2 раза меньше задач. Саша и Маша вместе могут решить 20 этих задач за 2 ч. За сколько часов Саша самостоятельно может решить 20 задач? Задача 3. Токарь четвёртого разряда и его ученик за час вместе изготавливают 50 деталей. Ученику для изготовления 50 деталей требуется времени на 2 часа больше, чем требуется токарю для изготовления 120 деталей. Сколько деталей в час изготовляет токарь? 5. Релаксационная пауза. Быстро встали, улыбнулись, Выше-выше подтянулись. Ну-ка плечи распрямите, Поднимите, опустите. Вправо, влево повернитесь, Рук коленями коснитесь. Сели, встали, сели, встали, И за парты тихо сели. 6. Решение задач с двумя (тремя) переменными. При решении задач на работу нередко в условии задачи говорится о выполнении некоторого задания без указания конкретных единиц, в которых измеряется работа. В этом случае обычно принимают всю работу за единицу: А=1. Как правило, для составления уравнения или системы уравнений, буквами обозначаются в первую очередь производительности участников работы, а остальные величины вводятся по мере необходимости. Алгоритм решения текстовых задач. • Ввод переменных, т.е. обозначение буквами x, y, z,. величины, которые требуется найти по условию задачи. • Перевод условий задачи на язык математических соотношений, т.е. составление уравнений, неравенств, введение ограничения. • Решение уравнений или неравенств. • Проверка полученных решений на выполнение условий задачи. Указания к решению текстовых задач • Набор неизвестных должен быть достаточным для перевода условий задачи на язык математических соотношений. Как правило, за неизвестные следует принимать искомые величины. • Выбрав неизвестные, в процессе перевода условий задачи в уравнения или неравенства необходимо использовать все данные и условия задачи. • При составлении уравнений или неравенств необходимо исходить из требования о решении задачи в общем виде. • В составленных уравнениях надо проверить размерность членов уравнений • В процессе решения задачи, надо избегать результатов, противоречащих физическому смыслу. Задача 4. Два экскаватора разной мощности, работая совместно, выполняют работу за 6 часов. Если первый проработает 4 часа, а затем второй 6 часов, то они выполнят 80% всей работы. За какое время каждый экскаватор отдельно может выполнить всю работу? Решение: Пусть Х-производительность первого экскаватора, а У- производительность второго экскаватора. Вся работа-1. Так как экскаваторы работают совместно 6ч с производительностью Х+У и выполняют всю работу, то составим уравнение: (Х+У)6=1. Первый экскаватор работает 4ч с производительностью Х., а затем 6ч второй экскаватор с производительностью У, и выполняют 0,8 всей работы, то 4Х+6У=0,8. Решим систему уравнений: Ответ: 10ч, 15ч. Задача 5. Первая труба и вторая, работая вместе, наполняют бассейн за 36 часов, первая и третья – за 30 часов, вторая и третья – за 20 часов. За сколько часов наполнят бассейн три трубы, работая вместе? 7. Подведение итогов урока. Рефлексия: Рефлексия. Оцените себя и сделайте для себя вывод о пользе проведенного на уроке времени. Учитель: У каждого из вас на столе карточки (зелёная, жёлтая, красная). Уходя из класса, оставьте на парте одну из них. Карточка зелёного цвета означает: Я доволен уроком, мне очень понравилось, я всё понял(а). Карточка жёлтого цвета означает: Мне понравился урок, но в моих знаниях есть пробелы. Карточка красного цвета означает: Я не доволен уроком, ничего не понял(а) и как решать, я не знаю. 8. Домашнее задание. Задачи для самостоятельного решения на раздаточном материале. Алгоритм решения текстовых задач. • Ввод переменных, т.е. обозначение буквами x, y, z,. величины, которые требуется найти по условию задачи. • Перевод условий задачи на язык математических соотношений, т.е. составление уравнений, неравенств, введение ограничения. • Решение уравнений или неравенств. • Проверка полученных решений на выполнение условий задачи. Указания к решению текстовых задач • Набор неизвестных должен быть достаточным для перевода условий задачи на язык математических соотношений. Как правило, за неизвестные следует принимать искомые величины. • Выбрав неизвестные, в процессе перевода условий задачи в уравнения или неравенства необходимо использовать все данные и условия задачи. • При составлении уравнений или неравенств необходимо исходить из требования о решении задачи в общем виде. • В составленных уравнениях надо проверить размерность членов уравнений • В процессе решения задачи, надо избегать результатов, противоречащих физическому смыслу. Задачи для самостоятельного решения Задача1. Два печника, работая вместе, могут сложить печь за 12 ч. Если первый печник будет работать 2 ч, а второй 3 ч, то они выполнят только 20 % всей работы. За сколько часов может сложить печь каждый печник, работая отдельно? Задача 2. Две бригады, работая вместе, могут закончить уборку урожая за 8 дней. Если первая бригада будет работать 3 дня, а вторая 12 дней, то они выполнят 75% всей работы. За сколько дней может закончить уборку урожая каждая бригада, работая отдельно? Задача 3.Два мастера, работая вместе, могут выполнить заказ за 6 ч. Если первый мастер будет работать 9 ч, а потом его сменит второй, то он закончит работу через 4 ч. За сколько времени может выполнить заказ каждый из мастеров, работая отдельно? Задача 4.Две машины, работая вместе, могут расчистить каток за 20 мин. Если первая машина будет работать 25 мин, а затем ее сменит вторая, то она закончит расчистку катка через 16 мин. За сколько времени может расчистить каток каждая машина, работая отдельно? Задача 5. Две трубы при совместном действии могут наполнить бассейн за 4 ч. Если бы сначала первая труба наполнила половину бассейна, а затем ее перекрыли и открыли вторую, то наполнение бассейна было бы закончено за 9 ч. За сколько времени может наполнить этот бассейн каждая труба в отдельности? Задача 6. Первый рабочий может выполнить задание за 8 ч, а второй за 6 ч. Они работали вместе 2 ч, а заканчивал задание один второй рабочий. Сколько времени потребовалось для выполнения второго задания? Задача 7. Двое рабочих, работая одновременно, выполнили задание за 5 дней. Если бы первый рабочий работал в 2 раза быстрее, а второй в 2 раза медленнее, то они выполнили бы задание за 4 дня. За сколько дней выполнил бы задание один первый рабочий? Задача 8. Бассейн наполняется водой из двух кранов. Сначала открыли первый кран на 1/3 часть того времени, за которое наполняет бассейн один второй кран. Затем был открыт один второй кран на ? часть того времени, за которое наполняет бассейн первый кран. После этого оказалось, что уже заполнено 5/6 объема бассейна. За какое время наполняет бассейн каждый кран в отдельности, если открытые вместе они наполняют бассейн за 2,4 ч? Задача 9. На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий? Задача 10. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша? Задача 11. Два каменщика, второй из которых начинает работать позже первого на 3 дня, могут выстроить стену за 14 дней. Первому каменщику потребовалось бы на выполнение этой работы на 6 дней больше, чем второму. За сколько дней может выстроить эту стену каждый каменщик в отдельности? Задача 12. Для разгрузки баржи имеется три крана. Первому крану для разгрузки всей баржи требуется времени в четыре раза меньше, чем второму, и на 9 часов больше, чем третьему. Три крана, работая вместе, разгрузили бы баржу за 18 часов, но по условиям эксплуатации одновременно могут работать только два крана. Определите наименьшее время (в часах) необходимое для разгрузки баржи.(Производительность каждого крана постоянна в течении всей работы) Ответ: 20ч. Задачи на совместную работу Основными компонентами задач, этого типа являются: а) Объём, выполняемой работы (А); б) Время работы (t); в) Производительность труда (работа, выполненная в единицу времени-N). План решения задачи обычно сводится к следующему: а) Принимаем всю работу, которую необходимо выполнить, за 1, если речь идет о выполнении некоторой работы, не охарактеризованной в количественном плане. б) Находим производительность труда каждого рабочего в отдельности, т. е. 1/t, где t – время, за которое указанный рабочий может выполнить всю работу, работая отдельно. в) Находим ту часть всей работы, которую выполняет каждый рабочий отдельно, за то время, которое он работал. г) Составляем уравнение, приравнивая объем всей работы (т. е. 1) к сумме слагаемых, каждое из которых есть часть всей работы, выполненная отдельно каждым из рабочих (если в условии сказано, что при совместной работе всех рабочих выполнен весь объем работы). Следует заметить, что в указанных задачах не всегда сравнивается выполненная работа. Основанием для составления уравнения может служить также указанное в условии соотношение затраченного времени или производительности труда. Задача. Два экскаватора разной мощности, работая совместно, выполняют работу за 6 часов. Если первый проработает 4 часа, а затем второй 6 часов, то они выполнят 80% всей работы. За какое время каждый экскаватор отдельно может выполнить всю работу? Решение: Пусть Х-производительность первого экскаватора, а У- производительность второго экскаватора. Вся работа-1. Так как экскаваторы работают совместно 6ч с производительностью Х+У и выполняют всю работу, то составим уравнение: (Х+У)6=1. Первый экскаватор работает 4ч с производительностью Х., а затем 6ч второй экскаватор с производительностью У, и выполняют 0,8 всей работы, то 4Х+6У=0,8. Решим систему уравнений: Поскольку время, необходимое для выполнения всей работы, и производительность связаны соотношением t = t =, то t =10ч, t =15ч. Ответ: 10ч, 15ч. Задача (Из “Арифметики” Л.Ф. Магницкого.) Один человек выпьет кадь пития в 14 дней, а с женою выпьет ту же кадь в 10 дней. Спрашивается, в сколько дней жена его отдельно выпьет ту же кадь. Старинное решение задачи:. За 140 дней человек выпьет 10 бочонков, а вместе с женой за 140 дней они выпьют 14 бочонков. Значит, за 140 дней жена выпьет 14 - 10 = 4 бочонка. Один бочонок она выпьет за 140 : 4 = 35 Интересная задача..Магазин в первый день продал половину привезённых гусей да ещё гуся; во второй день часть остатка да ещё гуся, а в третий день магазин продал оставшихся 33 гусей. Сколько всего гусей было привезено в магазин? Решение: Пусть было привезено в магазин х гусей. Тогда магазин продал: 1) в первый день гусей; 2) во второй день гусей; 3) в третий день 33 гуся. Составим уравнение и решим его. + +33=х, , -, х=101. Ответ: 101 гусь.