| 2. Подготовка учащихся к работе на основном этапе.

| 5 мин. | Обобщить полученные знания о правильных и неправильных дробях и смешанных числах. | Закрепить знания о правильных и неправильных дробях и смешанных числах. | Развивать внимание, мышление, память. | Объяснительно-иллюстративный. Метод иллюстрации. | Фронтальная работа. Индивидуальная работа. | Слайд № 3, 4, 5.
|
|
|
Учитель предлагает детям выполнить вычисления и обосновать свой ответ.
Два ученика у доски решают уравнения:
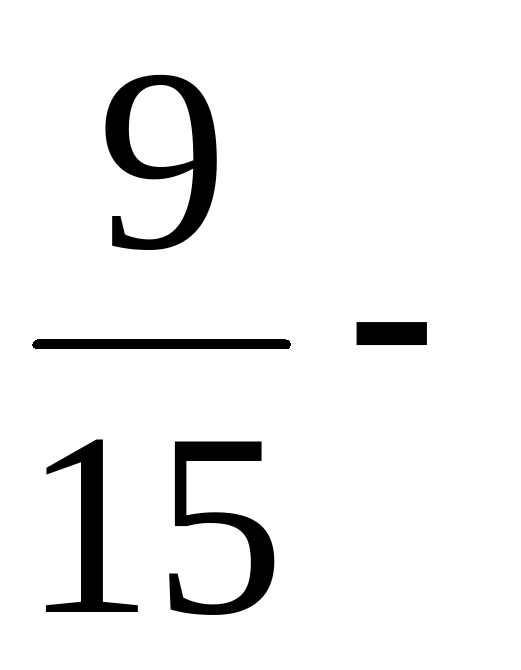  ( х + ( х +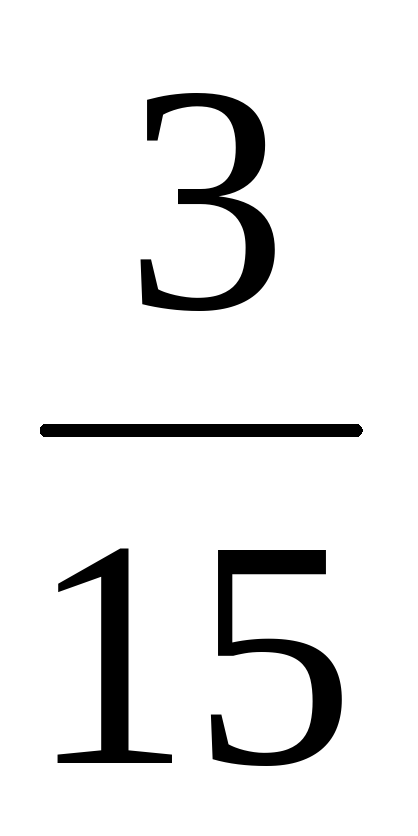 ) = ) =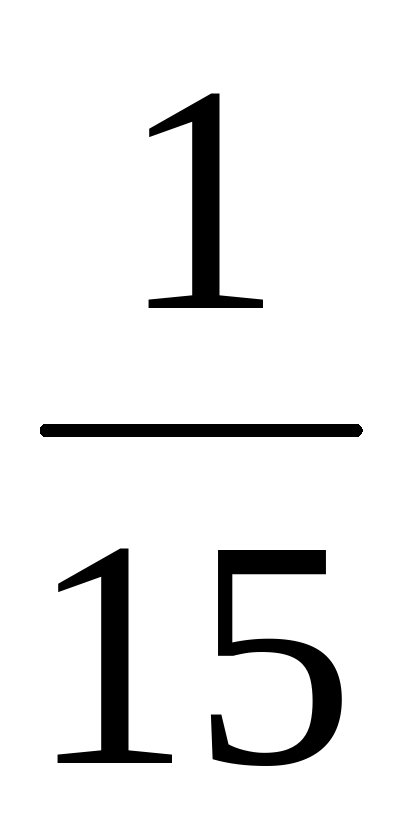  ( (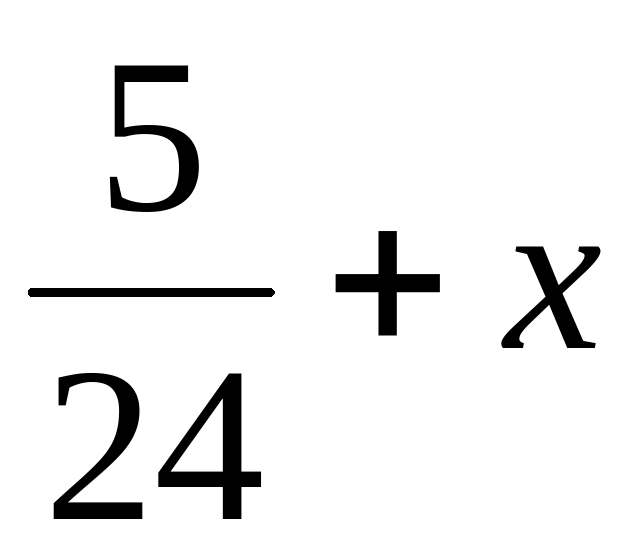 ) – ) – 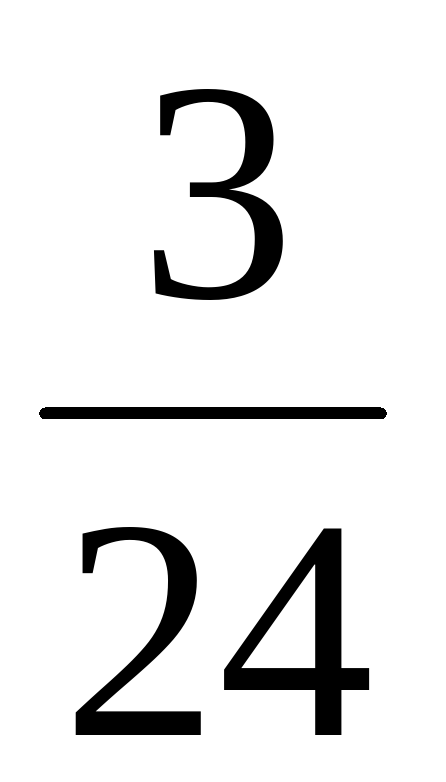 = =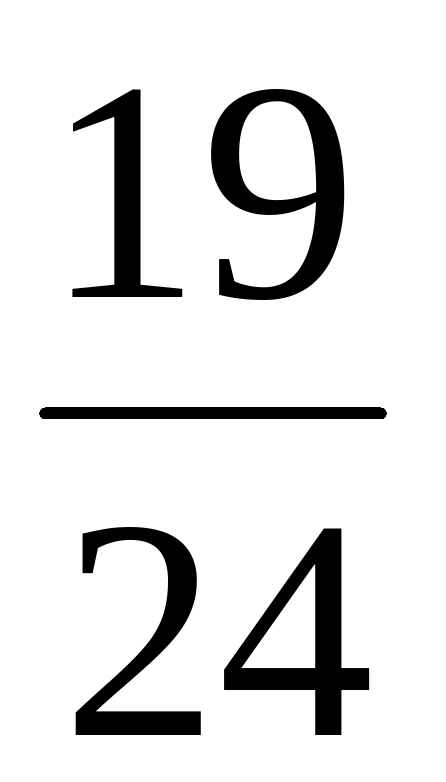  
Весь класс выполняет вычисления.
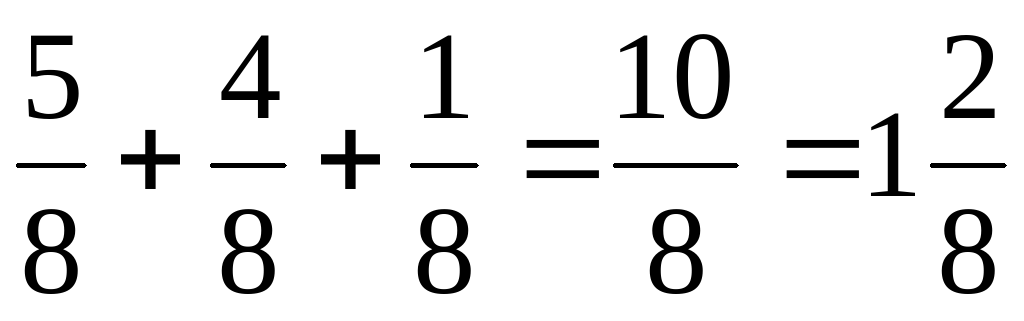 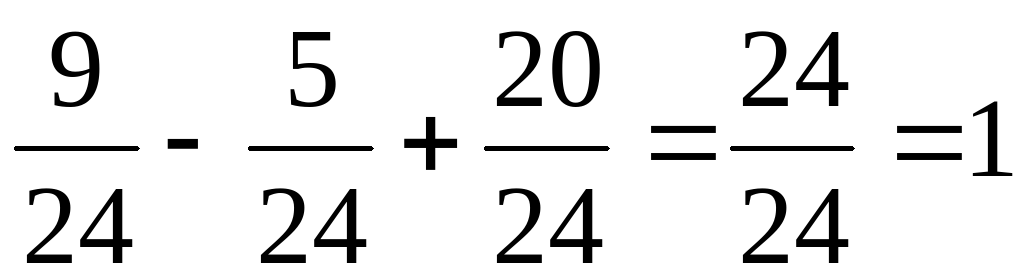
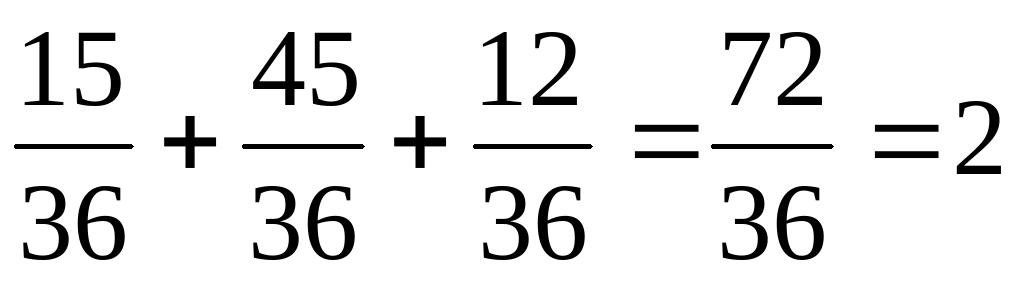 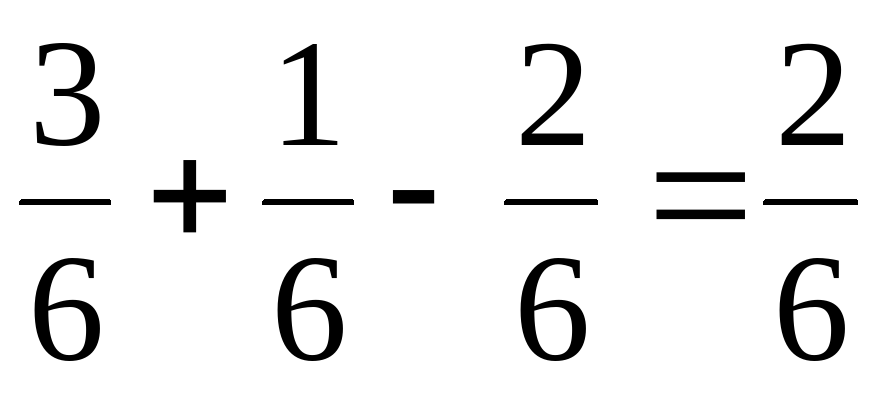
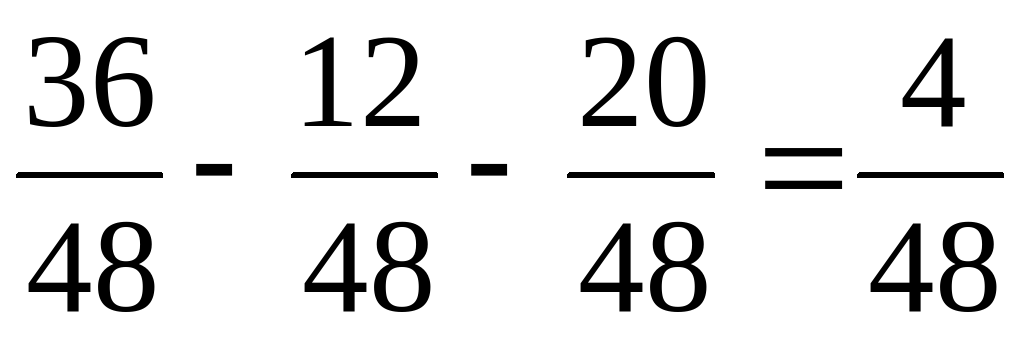 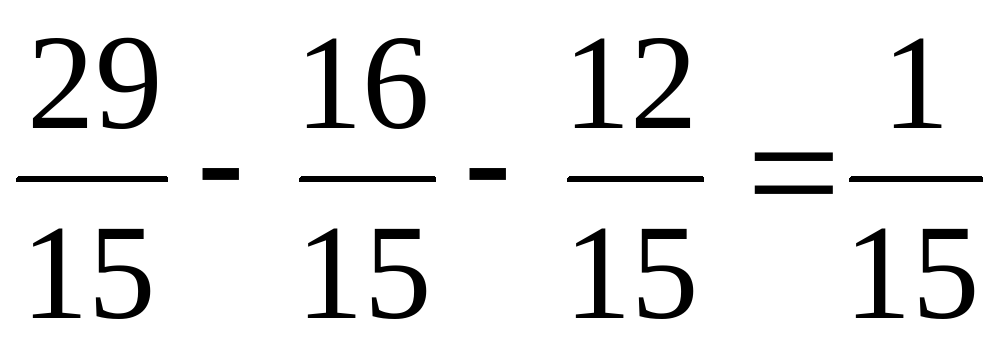
Назовите результаты вычислений. На какие группы можно разбить их? Назовите мне правильные дроби из примеров, неправильные, смешанные числа. Какие числа не назвали? Какие дроби называются правильными? Какие дроби называются неправильными? Что такое смешанное число? Какие числа называются натуральными? Что обозначают натуральные числа? Что обозначают дробные числа? Чем отличаются натуральные числа от дробных чисел? Дети по слайду №4 читают определения и приводят свои примеры. 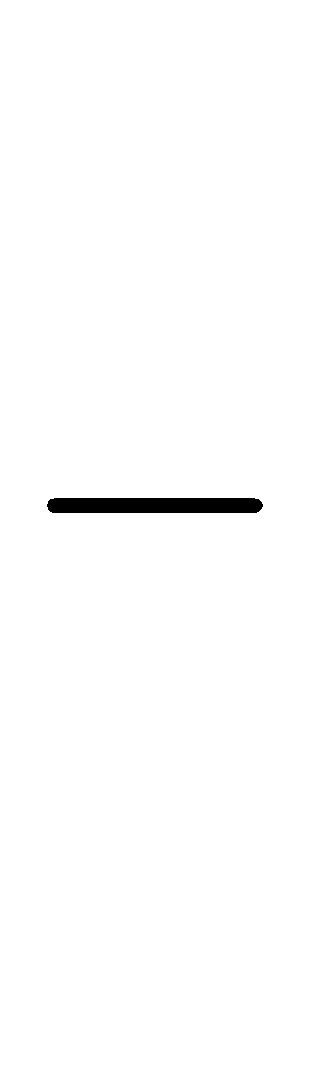 
Проверка решения уравнений.
|
Ученики находят ответ и дают обоснование своего решения.
2 ученика решают у доски уравнения.
Правильные, неправильные, смешанные, целые числа.
Дети называют дроби.
Дети дают определения.
Натуральные числа обозначают целые единицы, а дробные числа - часть единицы.
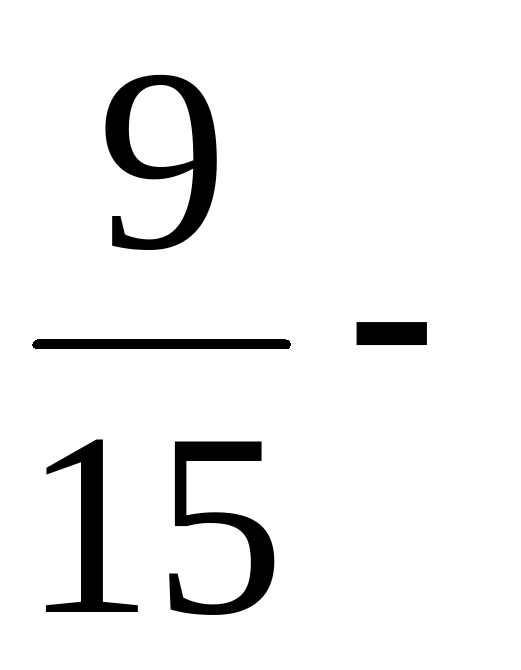  ( х + ( х +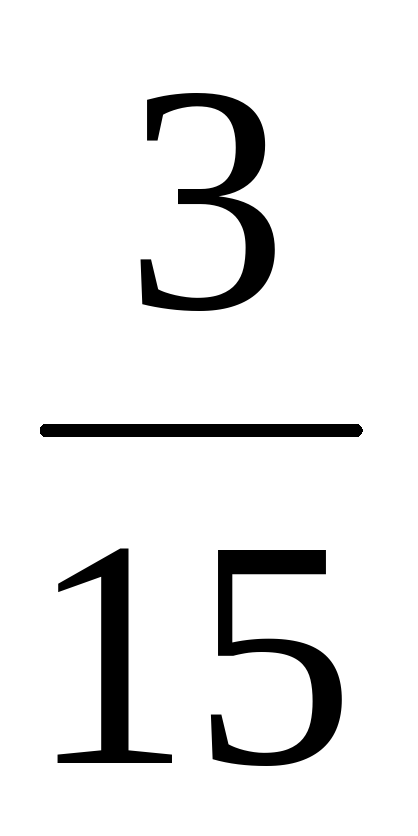 ) = ) =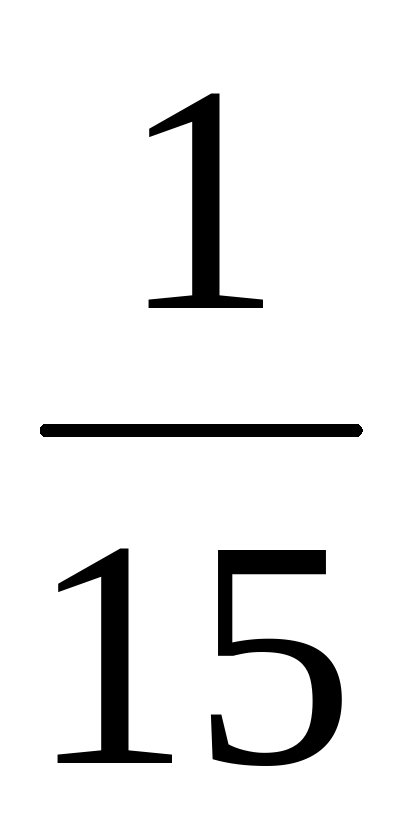  ( (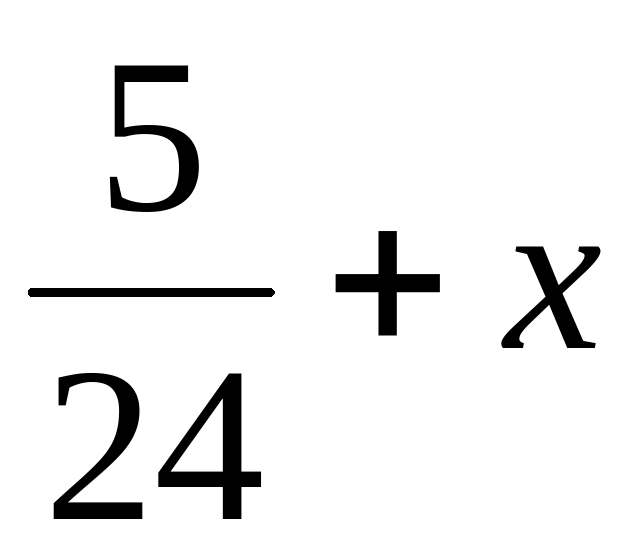 ) – ) – 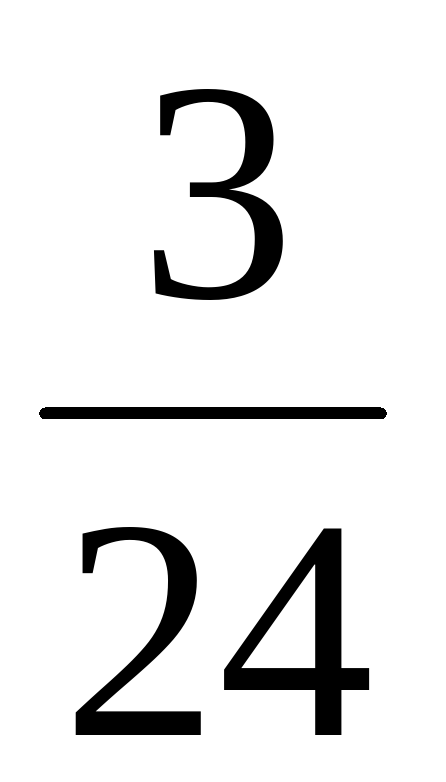 = =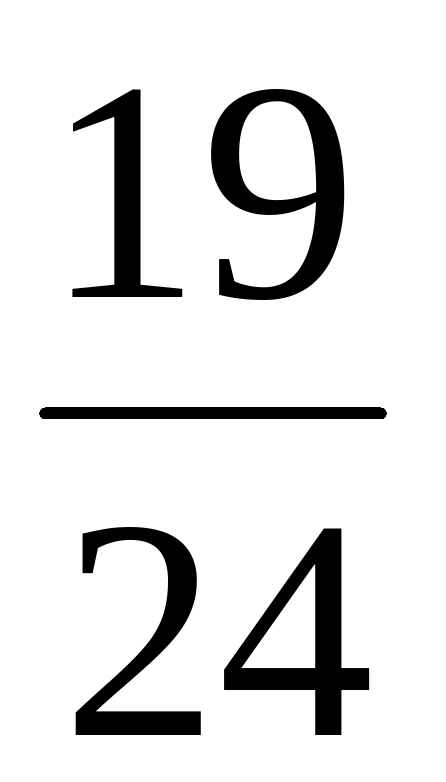
 Х + Х + 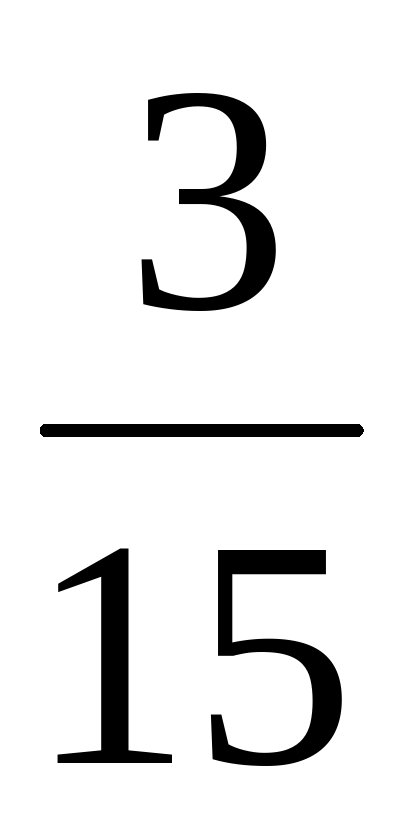 = = 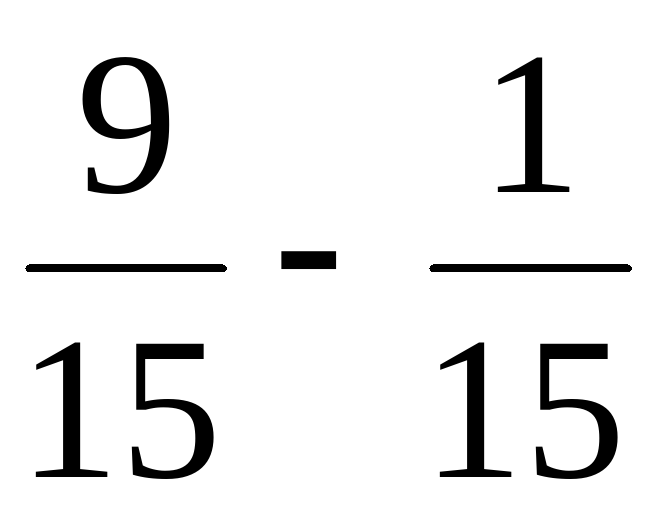 ( (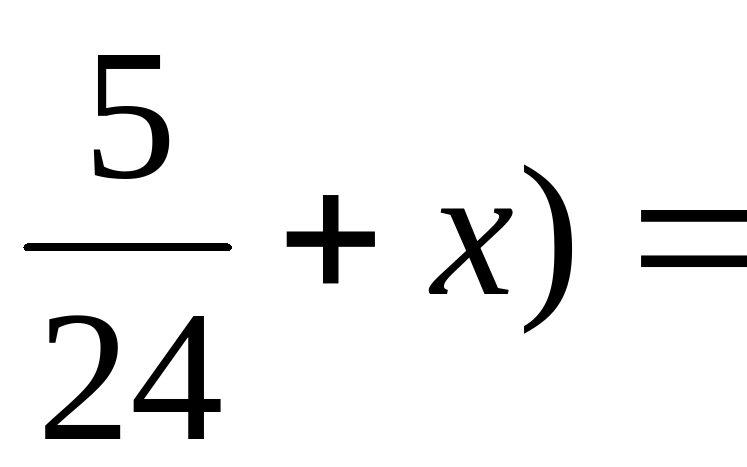 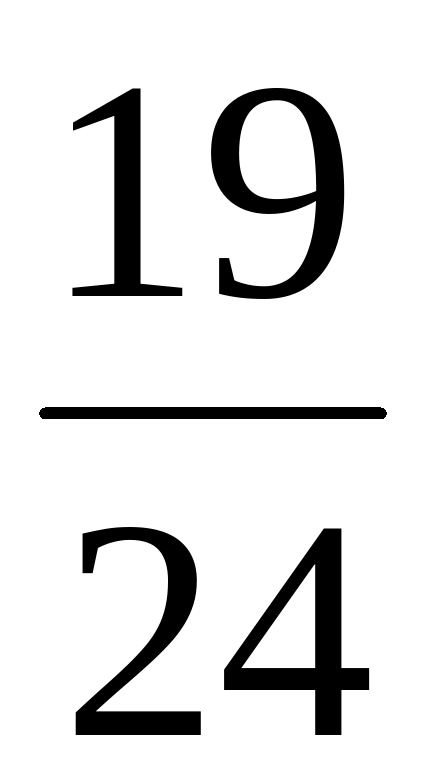 + +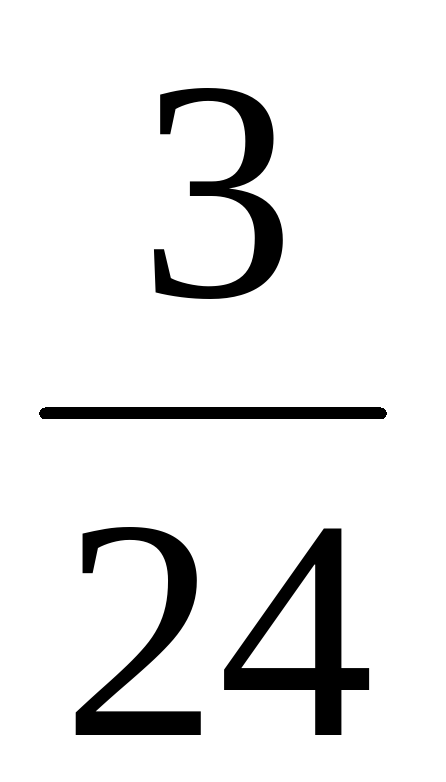
Х+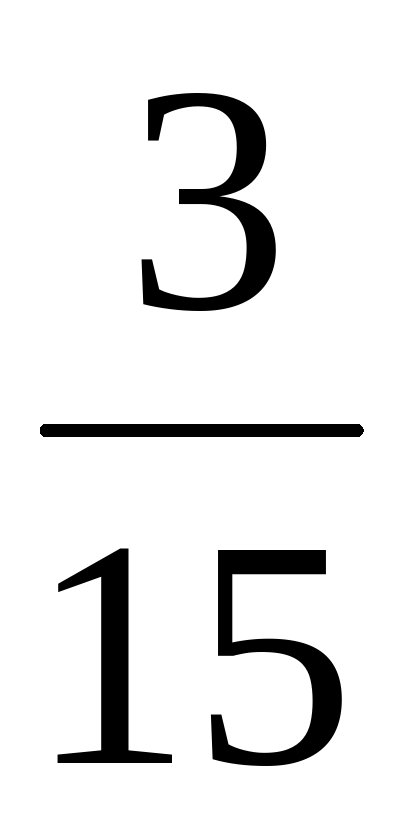 = = 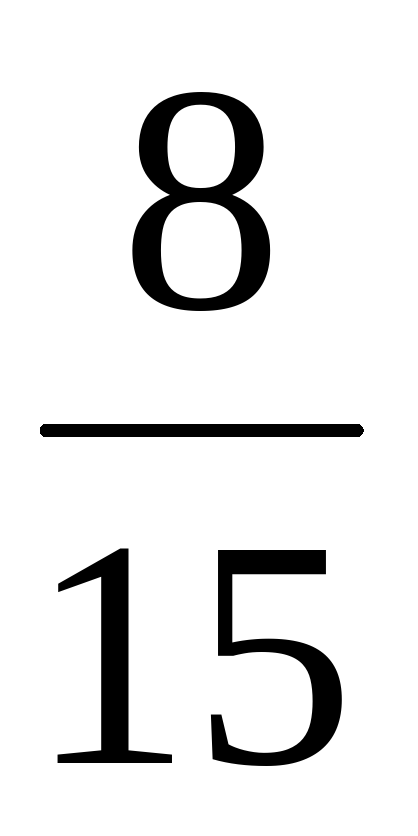 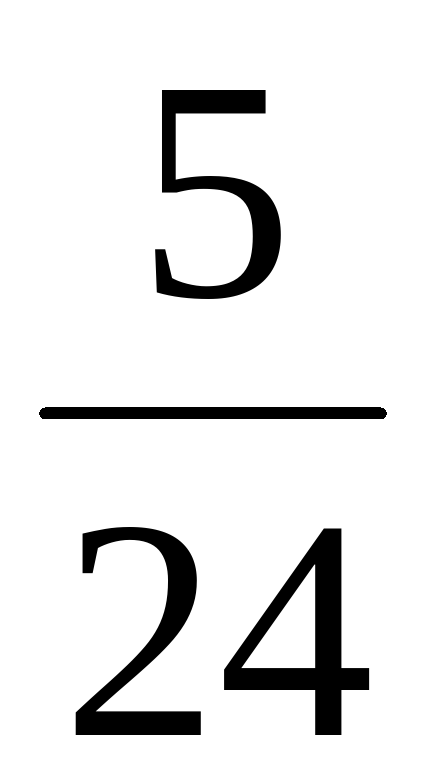 + х = + х =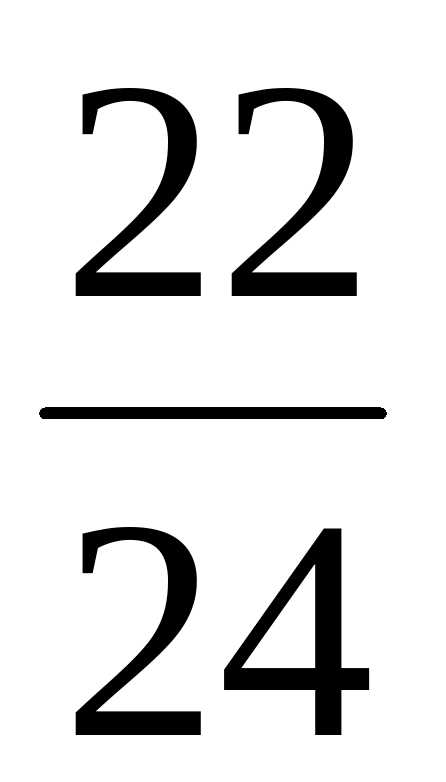 Х= 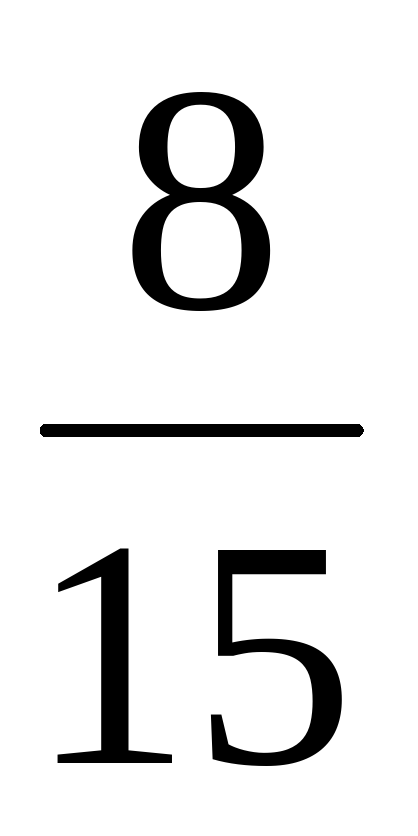 - -  Х = Х = 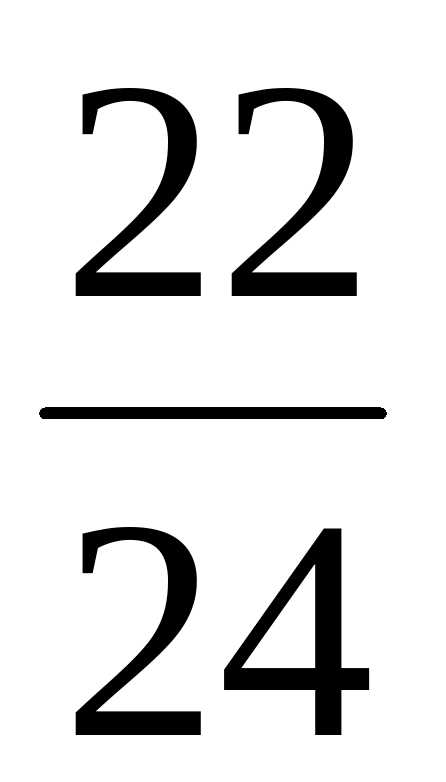 - -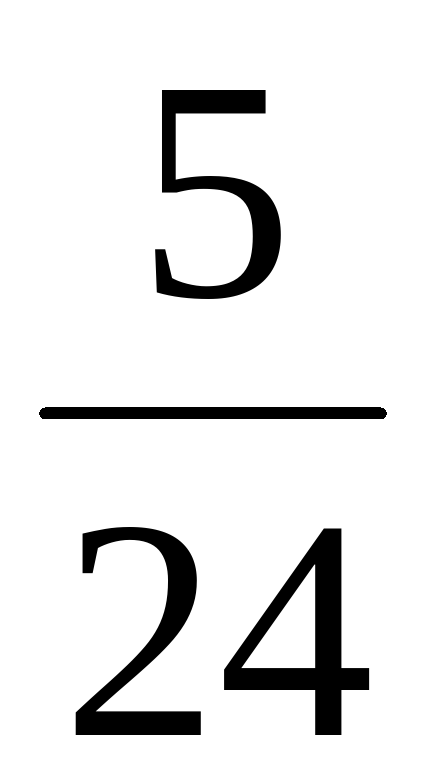 Х=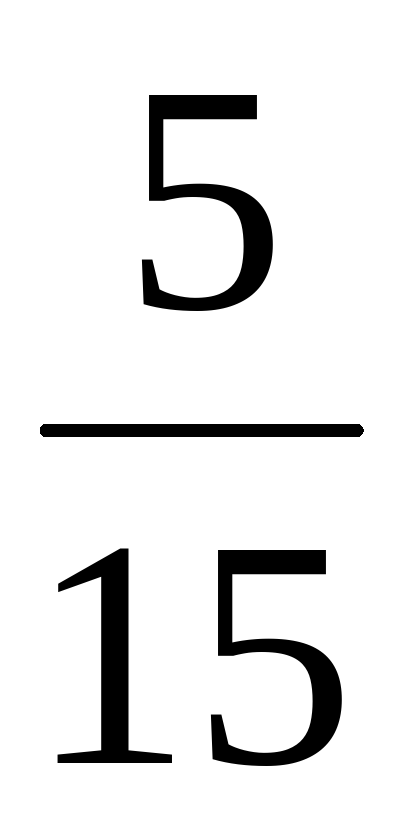 Х= Х=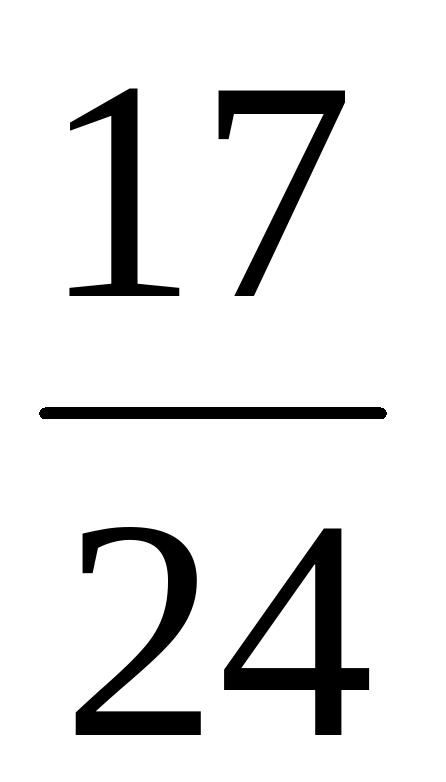
|
|
| 3. Этап воспроизведения учащимися знаний, умений и навыков, являющихся опорой для проведения и выполнения проверочных упражнений.
| 9 мин. | Повторить пройденное: формулы движения точек, построение чертежей, подготовить к введению нового знания. | Знать формулы движения точек, нахождение скорости удаления и скорости сближения. | Развивать умение анализировать формулы движения, читать схемы, чертежи. | Частично-поисковый, исследовательский.
| Фронтальная работа, групповая работа. |
Слайд № 6,7,8,9,10.
|
|
|
Какие числа использовали для записи формул? Что мы можем сказать об этих формулах?
Произойдет ли встреча?
Групповая работа. Дети получают карточки с заданиями: составить чертеж движения точек по формуле. После выполнения задания, ведущие ученики, объясняют решение своей задачи в других группах.
Х = 4 + 3 * t; Х = 19 – 2 * t
Х = 21 – 7 * t; Х = 13 – 5 * t
Х = 6 +3 * t; Х = 1 + 4 * t
Х = 8 + 6 * t; Х = 10 – 4 * t
После проведения консультации, работы учащихся выставляются на доску.
Дети самостоятельно решают задачи со слайдов №7,8,9,10.
Анализируют её, объясняют способ решения.
Что такое скорость сближения? Что такое скорость удаления? В КАКИХ СЛУЧАЯХ МЫ НАХОДИМ скорость сближения и скорость удаления? Как мы находим скорость сближения? Скорость удаления?
|
Натуральные числа, переменные х, t.
Точки движутся навстречу друг другу и встречаются через 4 минуты в координате 10. Точки вышли и движутся в противоположных направлениях, удаляясь друг от друга. Встречи не будет, они удаляются со скоростью 15ед/мин. Точки движутся друг за другом вдогонку, но встретиться не могут, так как вторая точка движется с меньшей скоростью. Точки движутся в одном направлении, так как у 2 точки скорость больше, то через 4 минуты она догонит точку 1.
Дети в группах выполняют задания и поднимают руки, когда группа будет готова.
Группа выбирает ученика для проведения консультации.
Ведущий ученик проводит консультацию и вывешивает свою работу на доску.
В этой задаче нужно найти расстояние между объектами за 3 часа, если они движутся со скоростью 4км/ч и 5км/ч. Для этого находим скорость сближения. Необходимо найти скорость объекта, для этого мы находим скорость сближения и из неё вычитаем известную скорость. Необходимо найти скорость объекта, для этого мы находим скорость сближения и из неё вычитаем известную скорость. В этой задаче необходимо найти время встречи. Мы должны расстояние разделить на скорость сближения.
|
|
 Х =
Х = 















