Тема урока: «Квадратные корни. Арифметический квадратный корень»
Цель урока: знакомство с понятиями «квадратный корень» и «арифметический квадратный корень», формирование умения находить значение арифметического квадратного корня.
Средства обучения: учебник «Алгебра 8» (авторы: Ю.Н. Макарычев и др.), таблица квадратов натуральных чисел, карточки с индивидуальными заданиями, лист самооценки работы в паре
Основные термины и понятия: квадратный корень, арифметический квадратный корень, знак корня (радикала), подкоренное выражение
| № | Этап урока | Задачи этапа | Деятельность учителя | Деятельность учащихся | Планируемые результаты |
| Личностные | Предметные | Метапредметные |
| 1 | Организационный момент | Создать благоприятную атмосферу на уроке, организовать начало учебной деятельности с первых минут урока | Учитель приветствует учащихся, проверяет их готовность к уроку. Учитель начинает урок с высказывания французского философа Ж.Ж.Руссо: «Вы талантливые, дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…» (Ж.Ж.Руссо) - Я желаю вам успешной работы на уроке и хорошего настроения!
| Приветствие. Учащиеся занимают свои места. Проверяют готовность к уроку.
| Формирование готовности учащихся к саморазвитию и личностному самообразованию | Формирование представлений о математике как о методе познания окружающей действительности | Формирование умения ставить и формулировать для себя новые задачи в учебе и познавательной деятельности |
| 2 | Мотивация учебной деятельности | Обеспечить мотивацию учащихся, побудить учащихся высказать свое мнение, уточнить понимание учащихся поставленных целей урока | Учитель формулирует тему урока: «Квадратные корни. Арифметический квадратный корень». Затем предлагает слова-помощники: «Изучим», «Узнаем», «Рассмотрим», «Научимся». -Ребята, сформулируйте цели урока, используя слова-помощники. | Учащиеся формулируют цели урока, используя слова-помощники | Формирование мотивации к обучению и целенаправленной познавательной деятельности | Развитие умения точно и грамотно выражать свои мысли с применением математической терминологии | Формирование умения самостоятельно определять цели своего обучения |
| 3 | Актуализация опорных знаний | Напомнить учащимся, как находить площадь квадрата, как возводить число в квадрат | Учитель предлагает задание. Найдите площадь квадрата со стороной 3 см; 10 см; a см. Самостоятельное решение в тетрадях с последующей проверкой | Учащиеся самостоятельно решают задачу в тетрадях, проверяют правильность выполнения задания. | Формирование готовности учащихся к познавательной деятельности | Овладение навыками устных вычислений | Формирование умения самостоятельно находить способ решения возникающих задач |
| 4 | Изучение нового материала | Сформировать понятие квадратный корень, понятие арифметический квадратный корень, научить читать выражения, содержащие квадратные корни | Работа с учебником с.74 п.12. Рассмотреть задачу. Пусть площадь квадрата равна 64 см2. Чему равна длина стороны квадрата? Ответ: 8. Корни уравнения x2=64, т.е. числа, квадраты которых равны 64 называют квадратными корнями из числа 64. Сформулируйте определение квадратного корня из числа. Найдите определение квадратного корня в учебнике. - Мы с вами узнали, что такое квадратный корень. Что же такое арифметический квадратный корень? Найдите в учебнике определение арифметического квадратного корня. Для обозначения арифметического квадратного корня ввели знак радикала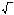 (лат. radex - корень). Запись 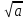 читают: квадратный корень из читают: квадратный корень из 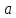 . . Выражение, стоящее под знаком корня, называют подкоренным выражением. Слово «арифметический» при чтении опускают. Рассмотрим примеры нахождения арифметических квадратных корней: 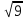 = 3, т.к. 32 = 9 и 30 = 3, т.к. 32 = 9 и 30
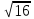 = 4, т.к. 42 = 16 и 40 = 4, т.к. 42 = 16 и 40
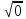 = 0, т.к. 02 = 9 и 0 – неотрицательное число. = 0, т.к. 02 = 9 и 0 – неотрицательное число.
Учитель подводит учащихся к определению арифметического квадратного корня в буквенном виде. Учитель дает подсказку. 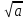 = =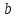 , если… , если…
Продолжите. Найдите формулировку в учебнике. Сравним с вашими предположениями. Как вы думаете, всегда ли 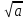 имеет смысл? (нет) Почему? (Т.к. квадрат любого числа неотрицателен). имеет смысл? (нет) Почему? (Т.к. квадрат любого числа неотрицателен). Тогда при каких 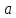 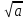 имеет смысл? имеет смысл? (при 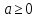 ). ). Приведите примеры выражений, не имеющих смысл, запишите их в тетрадь. Из определения арифметического квадратного корня следует: 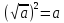 при при 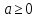 . .
Например, 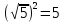
| Работают с учебником. Находят корни уравнения x2=64 методом подбора. Формулируют определение квадратного корня. Находят определение квадратного корня в учебнике. Находят определение арифметического квадратного корня. Записывают в тетрадь: 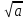 – квадратный корень из – квадратный корень из 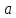 , где , где 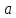 – подкоренное выражение. – подкоренное выражение.
Записывают примеры в тетрадь. Предлагают свои варианты определения арифметического квадратного корня в буквенном виде. Записывают в тетрадь: 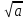 = =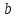 , если , если
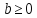
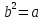 . .
Записывают в тетрадь выражения, не имеющие смысла: 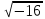 не имеет смысла. не имеет смысла.
Записывают в тетрадь: 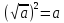 при при 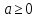 . .
Пример: 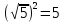
| Формирование готовности учащихся к саморазвитию и личностному самообразованию | Развитие умения точно и грамотно выражать свои мысли с применением математической терминологии | Формирование умения оформлять свои мысли в устной форме, умения искать и выделять необходимую информацию |
| 5 | Первичное закрепление знаний | Научить применять таблицу квадратов для нахождения значения арифметического квадратного корня, пользоваться определением арифметического квадратного корня для решения задач | Учитель вызывает к доске учащихся для выполнения следующих заданий: № 298 с.75 №300 с.75 Работа в парах. Учитель выдает индивидуальные карточки каждой паре. Один в паре – учитель, другой – ученик, затем меняются. Работа с таблицей квадратов. Пример карточки: Найдите значение корня: 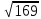 , , 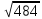 , , 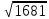 , , 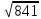 , , 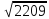
| Выполняют №298, №299(а,в) – самостоятельно, №300 Работают в паре | Формирование навыков составления алгоритма выполнения задания, навыков организации своей деятельности | Научиться применять приобретенные знания, умения, навыки для решения задач, научиться воспроизводить приобретенные знания, навыки в конкретной деятельности | Организовывать и планировать учебное сотрудничество с учителем и сверстниками, овладеть общим приемом решения учебных задач |
| 6 | Контроль | Организовать самостоятельное выполнение учащимися типовых заданий, самопроверку
| Задание №2 с. 58 в рабочей тетради «Алгебра,8 класс», авторы: Ю.Н. Макарычев, Н.Г. Миндюк и др. Задание можно вынести на слайд презентации, туда же добавить ответы, чтобы учащиеся могли выполнить самопроверку, критерии оценивания работы | Выполняют самостоятельную работу в тетрадях, осуществляют самопроверку, оценивают свою работу | Формирование навыков самоанализа и самоконтроля | Проанализировать допущенные в самостоятельно работе ошибки, проводить работу по их предупрежде- нию
| Оценивать уровень владения учебным действием (отвечать на вопрос «что я не знаю и не умею»). |
| 7 | Рефлексия | Акцентировать внимание на конечных результатах учебной деятельности обучающихся на уроке | На слайде презентации: Продолжите фразу Мне было интересно… Мы сегодня разобрались… Я сегодня понял, что … Мне было трудно… | Формулируют конечный результат своей работы, высказывают свое мнение, делятся впечатлениями об уроке | Формирование навыков самоанализа и самоконтроля | Научиться проводить диагностику учебных достижений | Уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации |
| 8 | Домашнее задание | Организовать обсуждение и запись домашнего задания | Учитель объявляет домашнее задание: П.12 с.74-75, №299(б,г), №301, №306 | Записывают домашнее задание в дневник | Формирование ответственного отношения к учению | Научиться применять приобретенные знания, умения, навыки для решения задач, научиться воспроизводить приобретенные знания, навыки в конкретной деятельности | Овладение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности |
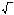
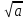 читают: квадратный корень из
читают: квадратный корень из 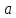 .
.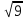 = 3, т.к. 32 = 9 и 30
= 3, т.к. 32 = 9 и 30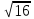 = 4, т.к. 42 = 16 и 40
= 4, т.к. 42 = 16 и 40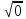 = 0, т.к. 02 = 9 и 0 – неотрицательное число.
= 0, т.к. 02 = 9 и 0 – неотрицательное число.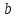 , если…
, если…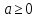 ).
).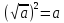 при
при 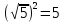
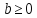
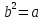 .
.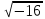 не имеет смысла.
не имеет смысла.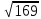 ,
, 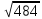 ,
, 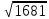 ,
, 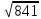 ,
,