МБОУ «Березовская основная общеобразовательная школа»
Залегощенского района Орловской области
Конспект открытого урока
по алгебре в 8 классе на тему:
«Квадратный корень из произведения»
(РМО учителей математики)
Учитель математики:
Казачкова И.К.
Тема урока: «Квадратный корень из произведения»
Цели урока:
- создать условия для вывода учащимися утверждения 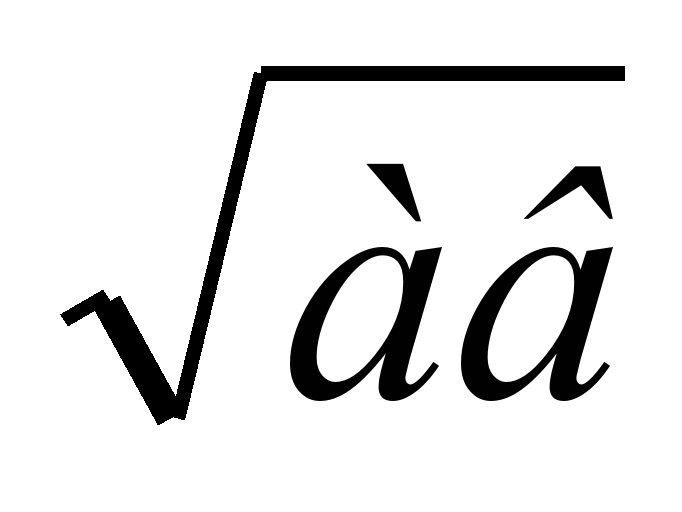 =
= 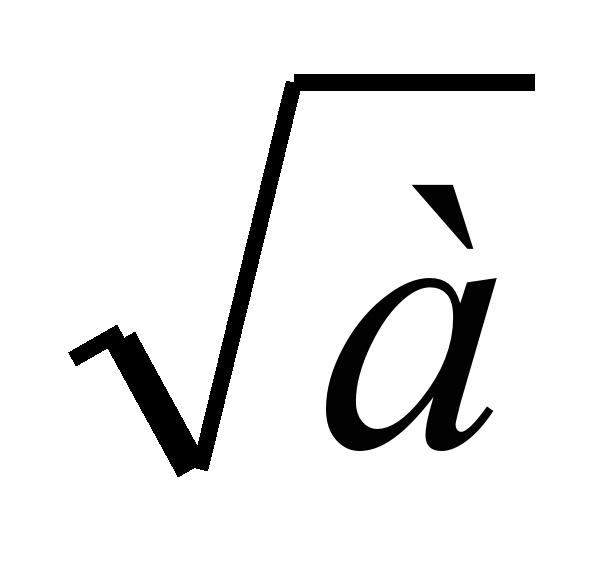
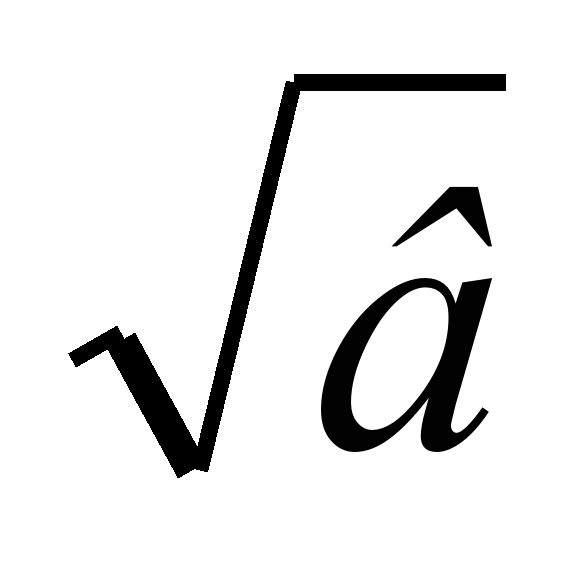 и применения его для вычисления квадратных корней;
и применения его для вычисления квадратных корней;
- способствовать развитию логики, умения проводить анализ и делать выводы;
- содействовать воспитанию уважительного отношения к себе и к своим товарищам, признавать право быть уникальным и право на ошибку.
Ход урока
Организационный момент.
На доске записано высказывание:
«Дороги не те знания, которые откладываются в мозгу,
как жир, дороги те, которые
превращаются в умственные мышцы»
Герберт Спенсер
Учитель:
- Ребята, перед вами высказывание. Как вы его понимаете?
Ученики высказывают свои мнения.
Учитель:
-Сегодня на уроке мы с вами будем превращать полученные знания в умственные мышцы.
Актуализация опорных знаний.
Найдите квадратные корни из чисел: 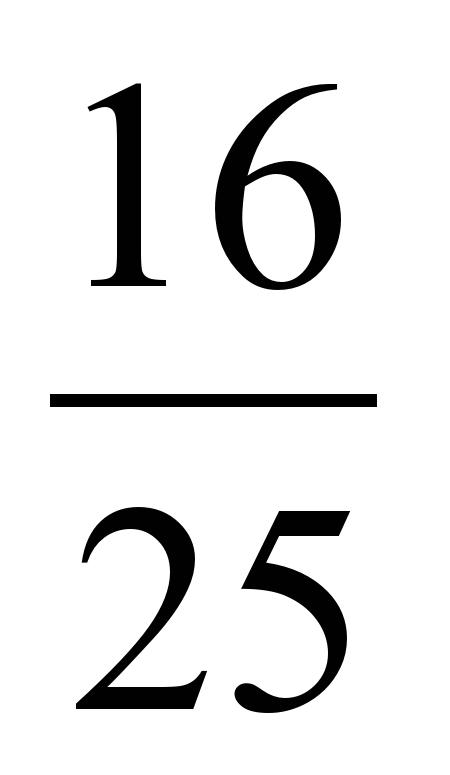 , 64, 0, -
, 64, 0, -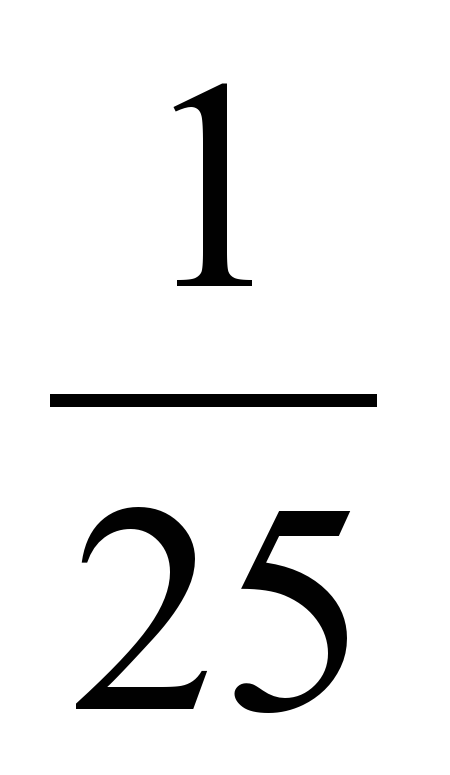 , 49 (числа записаны на доске заранее)
, 49 (числа записаны на доске заранее)
Учитель выслушивает разные варианты ответов и мнений учащихся.
Дайте определение квадратного корня из числа
От чего зависит наличие квадратных корней из числа а?
Учитель к написанным на доске числам дописывает значки арифметического квадратного корня.
Задает вопрос ученикам:
- Что нужно найти сейчас для этих чисел?
А чем отличается квадратный корень из числа а от арифметического квадратного корня из этого же числа?
При каких значениях а выполняется равенство |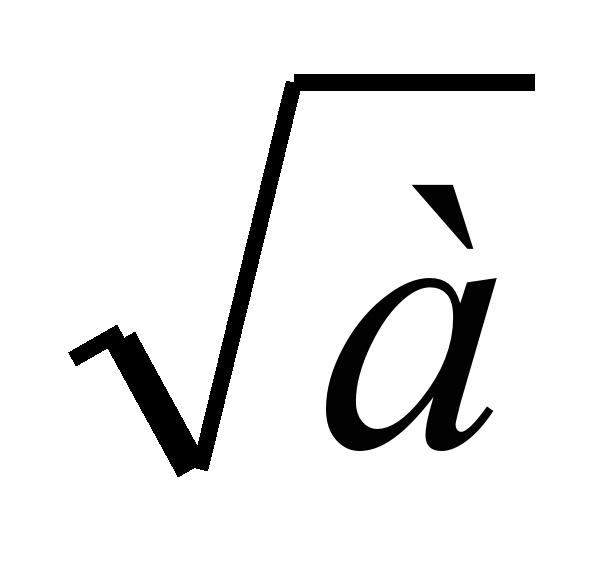 |2=а?
|2=а?
Тест
|
| Вариант 1 | Вариант 2 |
| 1 | 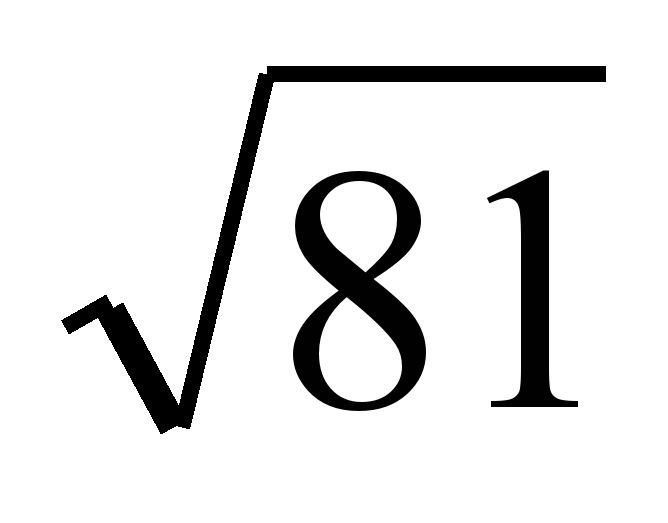
| 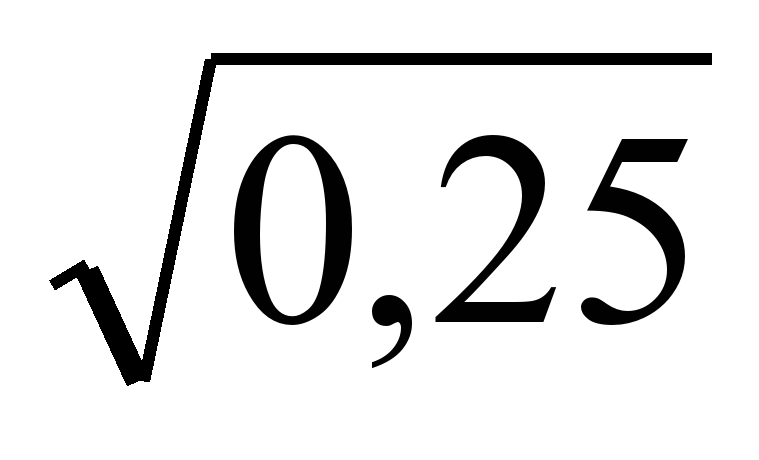
|
| -9, 9, 81 | 5, 0,5; -0,5 |
| 2 | ( )2 )2 | ( )2 )2 |
| 4; 2;  | - ; ;  ; ;  |
| 3 | 
| 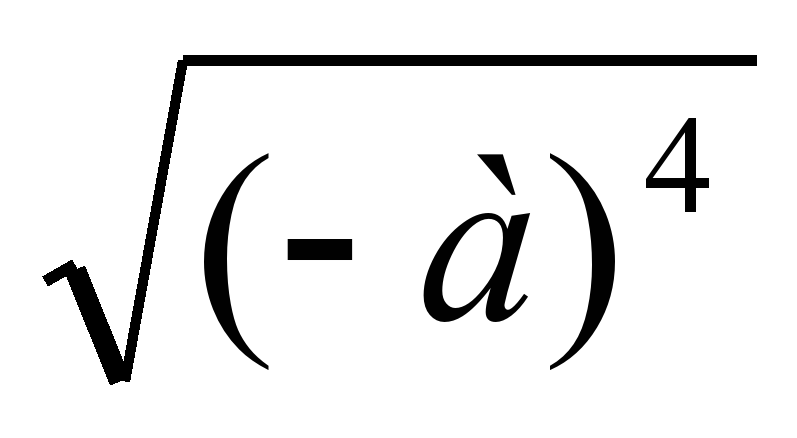
|
| х6; х2; х3 | -а; (-а)4; а2 |
| 4 |  или или 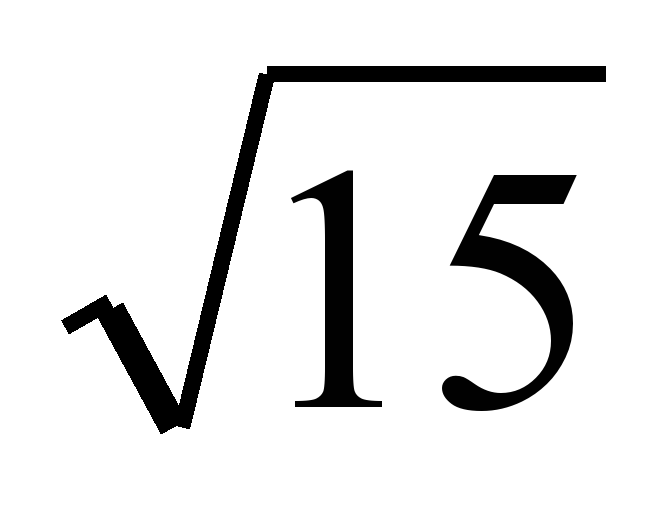
| 2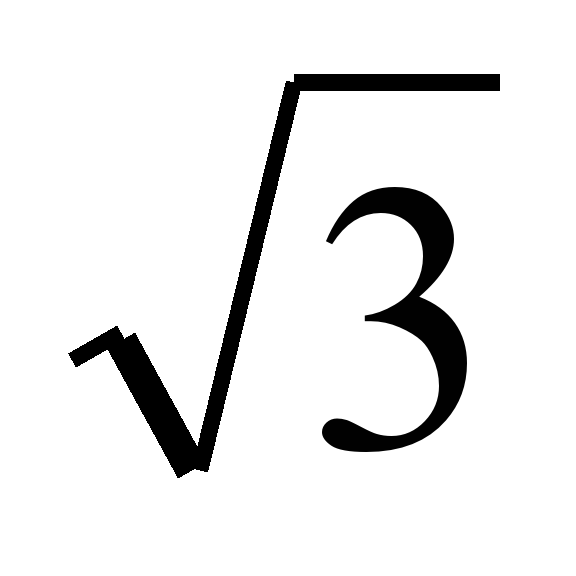 или 5 или 5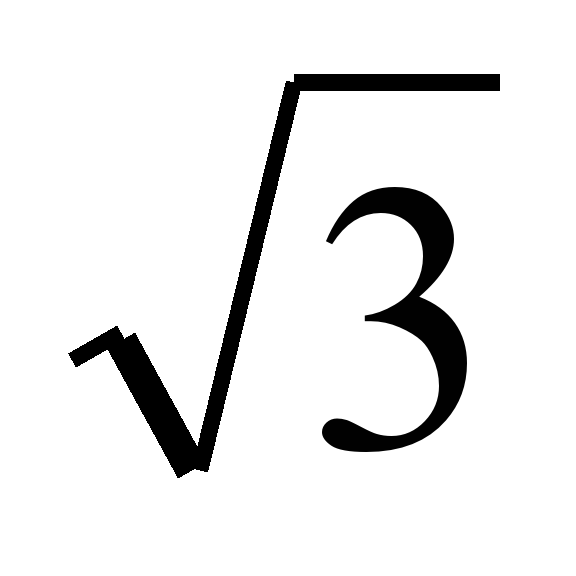 |
| , =, | , =, |
| 5 | 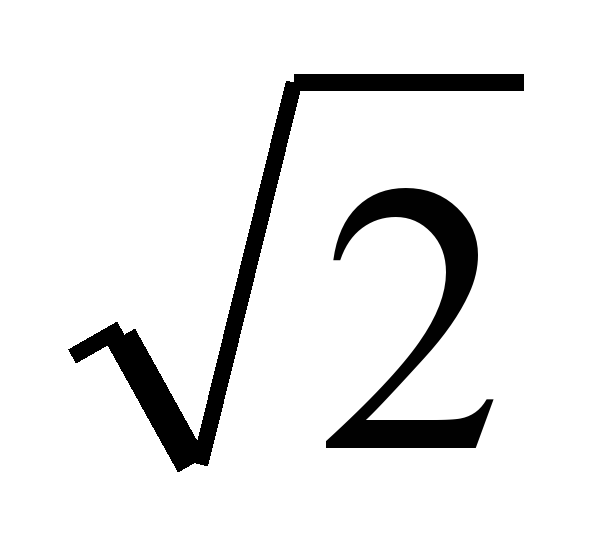 * *
| 
|
| 4; 2; 8 | 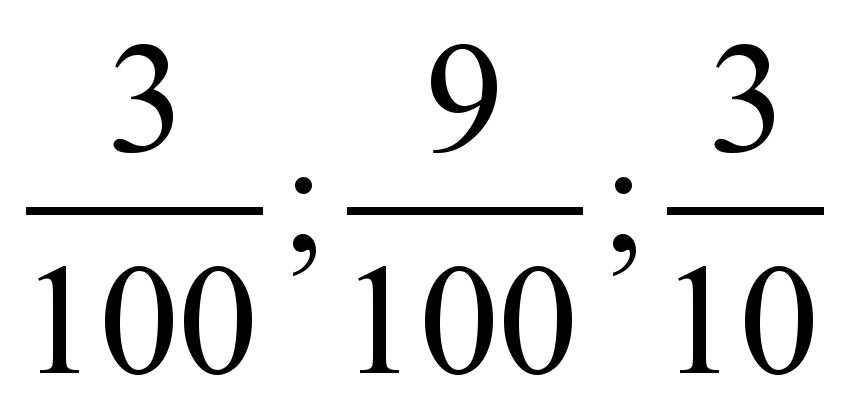
|
Изучение нового материала.
Разбейте тетрадный лист на три вертикальные части. В первый столбец запишите квадратные корни и вычислите их.
Во второй столбец запишите квадратные корни и вычислите их. Какой порядок действий при вычислениях?
В третий столбец запишите выражения и найдите их значения. Какой порядок действий при вычислениях?
Посмотрите внимательно на решения во всех трех столбцах. Какой вывод можно сделать?
- В каких столбцах вычисления для вас были легкими?
- Объясните, почему? Чем вы пользовались при вычислениях?
- Почему во втором столбце вычисления было сделать труднее?
- Сравните подкоренные выражения во всех трех столбиках. Какой вывод можно сделать?
(Учитель выслушивает различные варианты ответов учащихся и подводит под правило)
- Кто может сформулировать правило вычисления квадратного корня из произведения?
- Это правило справедливо для любых множителей?
- Запишите правило в общем виде, с помощью букв.
Работа с учебником.
На стр. 85 учебника прочитайте текст, найдите правило и сравните с тем, которое вы сформулировали.
Закрепление изученного.
№ 369 (а, в)
Учащиеся комментируют, а учитель у доски показывает оформление.
№ 369 (б, г, е)
Учащиеся комментируют и записывают самостоятельно.
Учитель:
- Можно ли применить правило для трех и более множителей?
№ 372 (а, б. в)
Учитель проверяет решение в тетрадях, дает консультации.
№ 383 (а, в, ж, д)
Учитель осуществляет индивидуальную помощь.
Рефлексия.
Заранее на доске приготовлено задание:
а) 
б) 
в) 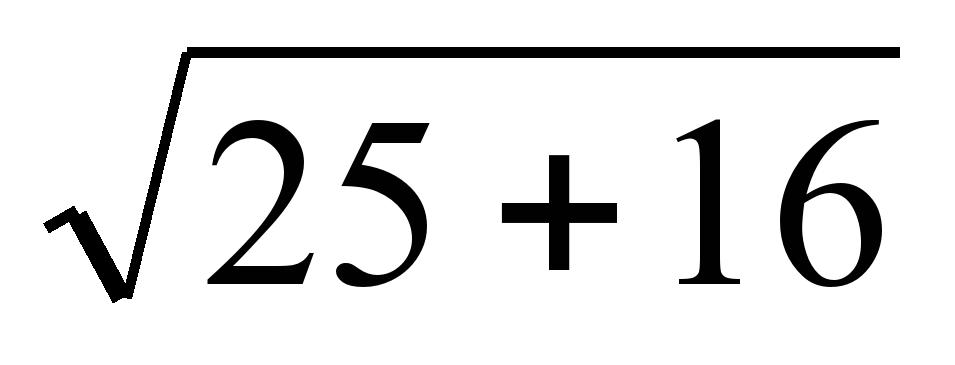
- Верно ли, что значения указанных квадратных корней можно найти по свойству квадратного корня из произведения?
Ученик вычислил значение  и получил два варианта ответа 1 и 5. Какой из них верный? Объясните.
и получил два варианта ответа 1 и 5. Какой из них верный? Объясните.
Итог урока.
Выставить отметки за урок, объяснить домашнее задание.
Домашнее задание: п.15 (стр. 84-85) , № 370, 373.


















