Метапредметный урок в 5 классе.
История чисел (математика и история).
Цели урока:
Ознакомить учащихся с историей возникновения чисел.
Применить полученные знания.
Развить мировозрение и кругозор учащихся.
Оборудование: мультимедийное оборудование, презентация к уроку.
План урока:
1. Вступительное слово учителя математики (2-3 мин).
2. Учитель истории об истории чисел.(10-15 мин).
3. Решение исторических математических задач (10-15 мин).
4. Подведение итога урока (5-7 мин).
5. Резерв времени (3-5 мин) (интересные задачи).
Учитель математики. (слайд 1)
Однажды был объявлен конкурс на тему “ Как жил человек без математики ?”. Победителю была обещана большая премия, но она так и осталась невыданной. Фантазии оказались бессильны – невозможно представить жизнь человека, лишенного математических знаний. Известные вам числа появились в глубокой древности для счета предметов. Такие числа называют натуральными. Назовите самое маленькое натуральное число, самое большое? (1. не существует). Самого большого натурального числа не существует, это было доказано древнегреческим ученым Евклидом.В древние времена было много способов счета предметов, результаты которых записывались с помощью различных символом, которые в современной математике называются цифрами. О происхождении слова “цифра”, записи чисел и другом вам расскажет учитель истории.
Учитель истории.(слайд 2,3)
Способов счета было придумано не мало : делались зарубки на палочке по числу предметов, завязывались узлы на веревке, складывались в кучу камешки. Но палку с зарубками с собой не возьмешь, да и камни таскать не очень приятно. И тут на помощь приходят пальцы рук – отличный счетный материал. Но что делать, если предметов больше десяти. Так была придумана десятичная система, которой мы пользуемся сейчас. Но этим путем пошли не все страны, хотя использовали все те, же пальцы. У древних инков для запоминания счета использовали зарубки, узелки и т. д. Есть еще и более экзотические варианты систем исчисления. Вавилоняне в научных расчетах использовали шестидесятичную систему, увековеченную в нашем делении круга на 360*, часа на 60 минут и минуты на 60 секунд. А одно из папуасских племен использует до сих пор двоичную систему счисления, которая, кстати, нашла свое место в современных компьютерных установках. Например
Египтяне вели запись чисел иероглифами на папирусе , который плохо сохранялся. До настоящего времени об этих математиках мало сведений. В древнем Китае цифры обозначались специальными иероглифами, которые появились во втором тыс. до н. э. , Эти иероглифы применяются и в настоящее время. Вавилоняне использовали клинописные значки на глиняных табличках, которые дошли до наших дней. Но все же богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных доказательной базы. Систематический подход в изучении математике появился только у древних греков.
- Математика в современном ее понимании этого слова родилась в Греции. В странах, современниках Эллады, математика использовалась либо для обыденных нужд, либо, наоборот, для магических ритуалов. Они не стали выдумывать новые значки для цифр, а использовали буквы. (слайд 4) Единицу обозначали буквой- А, двойку- В и т. д. Греческий алфавит похож на русский и поэтому такая система записи чисел пришла в Древнюю Русь. Пифагорейская школа ( основатель Пифагор ) (слайд 5) выдвинула тезис « Числа правят миром», “ Все есть число”. Ученики школы обожествляли числа и наделяли их невероятными свойствами.(слайд 6)Число 1 означало огонь, 2 – землю, 3- воду, 4- воздух. Две тысячи лет спустя Галилей сказал: « Природа разговаривает с нами на языке математике». (слайд 7) Это означало, что истины математики есть в известном смысле истины реального бытия.
Все эти системы, записи остались в древности, а древнеримскими и арабскими цифрами мы продолжаем пользоваться и сейчас. (слайд 8) Римские цифры употреблялись в Древнем Риме уже около 2500 лет тому назад. I- 1, Y- 5, X - 10, L - 50, C - 100,D - 500 , M – 1000. Остальные числа записывались этими цифрами с применения сложения и вычитания, если меньшая по значению цифра стоит перед большей, то ее значение вычитается, например, XC означает 90.
В настоящее время римские цифры обычно применяются при нумерации глав книг, месяцев года, дат значительных событий, годовщин. Для вычислений запись чисел с помощью римских цифр неудобна.
Современная десятичная система записи чисел была заимствована европейцами у арабов, которые в свою очередь переняли ее у индусов. Поэтому эти цифры мы называем “арабскими”, а арабы - “индийскими”. Индийские математики вместо отсутствующего разряда в числе использовали кружок, арабские математики назвали такой рисунок “сифр” , а уже в Европе это слово зазвучало как “цифра”. Долго под цифрой понимали единственный значок 0. Около 500 г. Н. э. неизвестный нам великий индийский математик изобрел новую систему записи чисел – десятичную позиционную систему.
Учитель математики. Давайте вспомним какие это цифры. (слайд 9) Стихотворение (читают два учащихся):
Вот один, иль единица, очень тонкая, как спица. (1 уч)
А вот это – цифра два, полюбуйтесь какова(2 уч)
Выгибает двойка шею, волочится хвост за нею.(2 уч)
А за двойкой, посмотри, выступает цифра три. (1 уч)
За тремя идет четыре, острый локоть оттопыря,(2 уч)
А потом пошла плясать по бумаге цифра пять. (1 уч)
Руку вправо протянула, ножку круто изогнула. (1 уч)
Цифра шесть – дверной замочек: сверху крюк, внизу кружочек.(2 уч)
Вот семерка – кочерга, у нее одна нога.(1 уч)
А восьмерка – два кольца, без начала и конца. (2 уч)
Цифра девять иль девятка – цифровая акробатка.(1 уч)
Цифра вроде буквы “О”, это нуль, иль ничего.(2 уч)
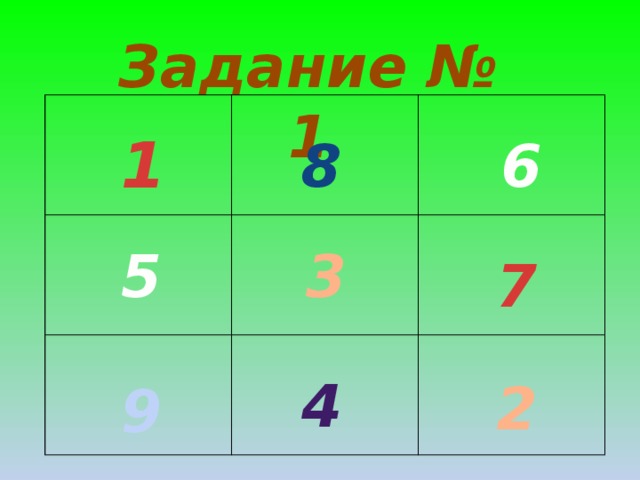
А теперь попробуем выполнить такое задание. Расставить цифры от 1 до 9 включительно в данный квадрат, так чтобы в каждой строке и каждом столбце сумма была одинаковая ( равнялась 15)
(Ответ) (слайд 10)
1 8 6
5 3 7
9 4 2
Если кто-то хочет можно усложнить задачу и добавить, чтобы и по обеим диагоналям тоже получилась такая же сумма. ( Ответ)
4 9 2
3 5 7
8 1 6
Учитель истории. Кстати, эта задача пришла к нам из древности. При археологический раскопках в Китае и Индии были найдены квадратные амулеты, предназначенные для решения этой задачи. С древних времен людям приходилось не только считать предметы 9 для чего требовались натуральные числа), но и измерять длину, время, площадь, вести расчеты при продаже. Не всегда результат измерения улавалось выразить натуральным числом. Приходилось учитывать и части, так появляются дроби. В русском языке слово дробь появилось в восьмом веке, оно происходит от глагола “дробить”. В первых учебниках математики дроби так и называли “ломанные числа”. Современное обозначение дробей берет свое начало в Древней Индии; его стали использовать и арабы, от них в 13-14 веках оно было заимствовано европейцами.
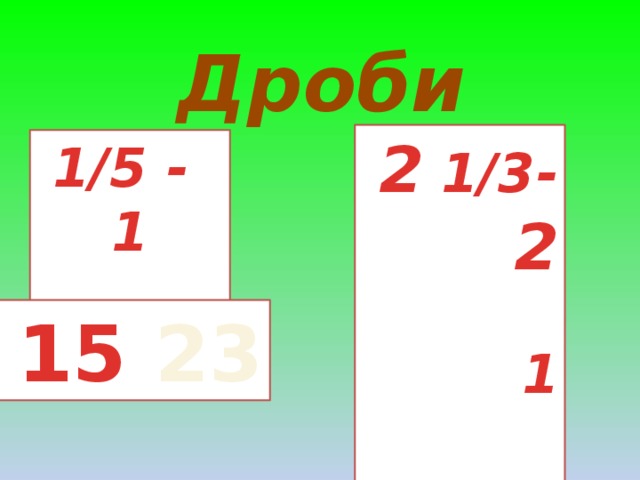
Учитель математики. Да, действительно, вначале в записи дробей неиспользовалась дробная черта: (слайд 11) например 1/5 писали 1 5,
Черта дроби стала постоянно использоваться около 300 лет назад. Название “числитель” и “знаменатель” ввел в 13 веке греческий монах ученый-математик Плануд. Теперь вы уже знаете, что кроме обыкновенных дробей существуют и десятичные дроби. Так вот при различных расчетах их используют чаще, чем обыкновенные. Как вы думаете с чем это связано ? Ответ Это связано с похожестью правил вычисления десятичных дробей и натуральных чисел. В этом мы с вами убедимся изучая дальше тему “Десятичные дроби”. Правила вычисления с десятичнымидробями описал знаменитый ученый Средневековья аль- Каши Ибн Масуд в начале 15 века. Он записывал десятичные дроби не так как прнято сейчас, он не использовал запятую, дробную часть он записывал красными чернилами или отделял чертой. Запятая для отделения целой части стала использоваться с 17 века. Раньше писали 15 23, выделяя целую часть другим цветом.
Учитель истории. В разные времена у разных народов получили различные названия единцы длины, веса, площади. (слайд 12, 13)
Например: в древней Руси в качестве измерения применялись: косая сажень(248 см) – расстояние от пальцев левой ноги до конца пальцев полнятой правой руки; маховая сажень (176 см) – расстояние между концами пальцев расставленных в сторону рук; локоть (45 см) – расстояние от концов пальцев до локтя согнутой руки и другие. В 17 веке Петр 1 упорядочил систему мер в России, ввел довольно сложные соотношения между бытовавшими в то время единицами: 1 миля = 7 верст = 3500 саженей =10500 аршин =168000 вершков =294000 дюймов.
Затем был введен эталон измерения метр , (слайд 14) но есть страны, например США и Великобритания, где еще обходятся средневековыми мерами длины.
Учитель математики.(слайд 15) Выразите в современных единицах длины
а). Ширину горницы, равную 2 косые сажени и 3 локтя (Ответ 2*248+ 3* 45=385 (см)= 3м 85 см.)
б).Длину отреза полотна, равную 3 маховые сажени и 4 локтя (Ответ 3*176+ 4*45=708 см= 7м 8 см.)
Итог урока. Учитель математики. Надеюсь, что сегодняшний урок вам понравился, вы увидили необходимость использования математики с древнейших времен и до наших дней. (слайд 16) . Недаром говорят “Математика – царица наук”.
Итак, сегодня мы провели интересный, любознательный урок, на котором вы получили много полезной информации. Спасибо всем за урок.
Резерв времени. (Если останется время на уроке).
Учитель истории.
Первые единицы длины были связаны с размерами частей тела человека. Такова сажень, локоть, пядь, о которых мы уже говорили. В Англии и США до сих пор используется “ступня” - фут (31 см), “большой палец” - дюйм (25 мм), и даже ярд (91см) – единица длины, появившаяся почти 900 лет назад. , она была равна расстоянию от кончика носа короля Генриха 1 до конца пальцев его вытянутой руки.
Для измерения больших расстояний на Руси использовали единицу поприще, заменив позже верстой (от 500 до 750 сажень). От восточных купцов пошла единица аршин (тоже означает “локоть”)- существовал турецкий аршин, персидский аршин и др. Поэтому и возникла поговорка “мерить на свой аршин”. Множество единиц существовало и для измерения массы. Наиболее древняя русская мера – гривна. 9410 гр). Позднее появились золотники, фунты, пуды. В связи с развитием торговли назрела необходимость установить четкие определения единиц и соотношения между ними, что и было сделано при Петре 1.