Данный конспект урока можно использовать при обобщении темы "Арифметическая прогрессия". На уроке рассматривается решение задач прикладного характера, которые соответствуют определению арифметической прогрессии, а значит, при решении которых, можно использовать формулы n члена и суммы арифметической прогрессии.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
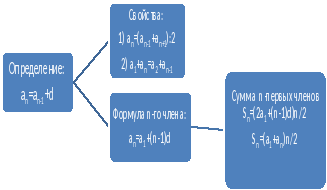
Использование формул арифметической прогрессии при решении прикладных задач.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Использование формул арифметической прогрессии при решении прикладных задач. »
Полезное для учителя
Распродажа видеоуроков!
1900 руб.
3170 руб.
1900 руб.
3170 руб.
1400 руб.
2330 руб.
1730 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


 Решение:
Решение: 10м/с_______________________________________3м/с, 8м/с, 11м/с….
10м/с_______________________________________3м/с, 8м/с, 11м/с….















