Интегрированный урок: «Решения систем уравнений с двумя неизвестными графическим способом»
(урок обобщения и систематизации знаний)
Цель урока: к концу урока учащиеся решают системы уравнений графическим способом вручную и с помощью программы SCILAB.
Задачи урока:
Актуализация опорных знаний. Устная работа;
Решения систем уравнений;
Практическая работа на компьютерах.
Ход урока:
Задание 1
Перед вами карточки с заданиями. Ответьте на вопросы. Ответы запишите прямо на карточках.
Является ли пара чисел (2; 3) решением системы уравнений?
а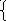
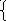
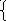 ) х2 + у2 = 13 б) х2 + у = 5 в) х2 + у2 = 4
) х2 + у2 = 13 б) х2 + у = 5 в) х2 + у2 = 4
2х + у = 7; 3х – 1 = у; 5х – 2у = 4
Какая из следующих пар чисел является решением системы уравнений?
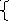 х2 + у2 = 1 а) (0; 1); б) (-1; -1); в) (1; 0) г) (1; 1)
х2 + у2 = 1 а) (0; 1); б) (-1; -1); в) (1; 0) г) (1; 1)
у – 2х = 1;
Устная проверка и запись результатов на интерактивной доске.
Устные ответы на вопросы:
Что значит решить систему уравнений?
Всегда ли есть решения в системе уравнений?
Система каких уравнений может иметь бесконечно много решений? (приведите пример);
Какие способы решения систем уравнений вам знакомы? (подстановки, алгебраического сложения, замены переменных, разложения на множители, графический).
Сегодня мы займемся графическим способом решения систем уравнений сначала вручную, а затем в компьютерном классе с помощью программы SCILAB.
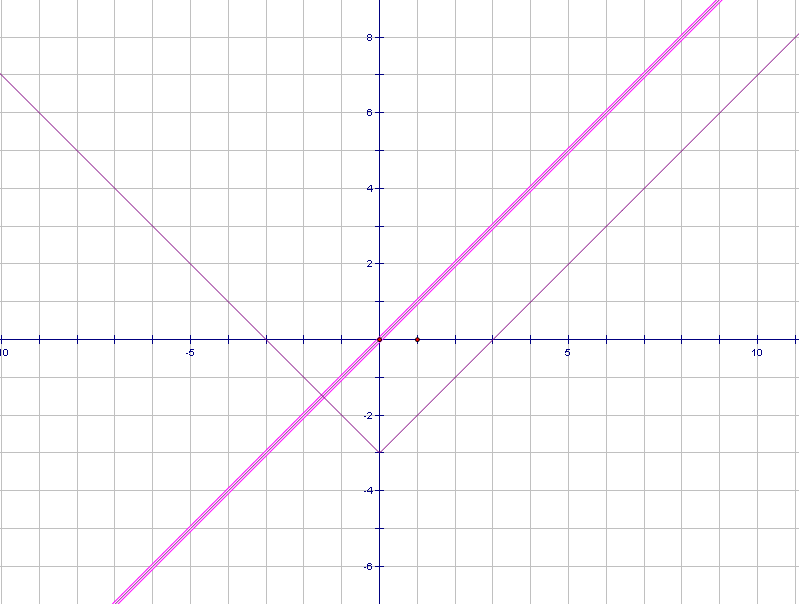
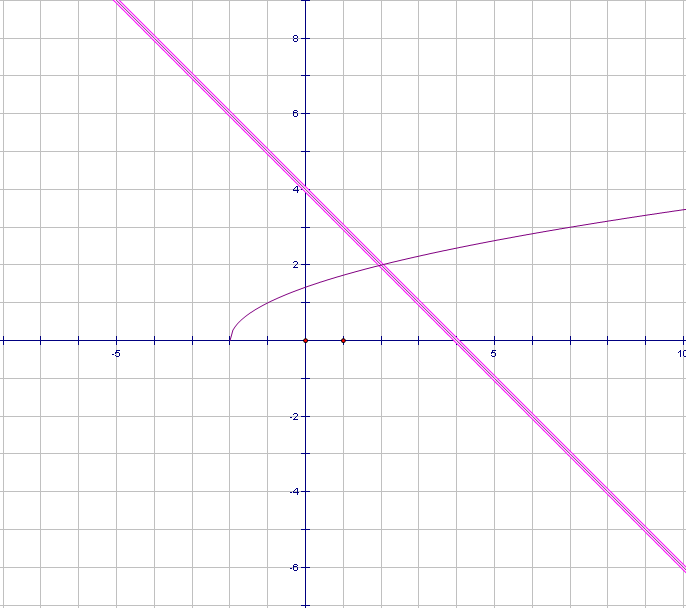
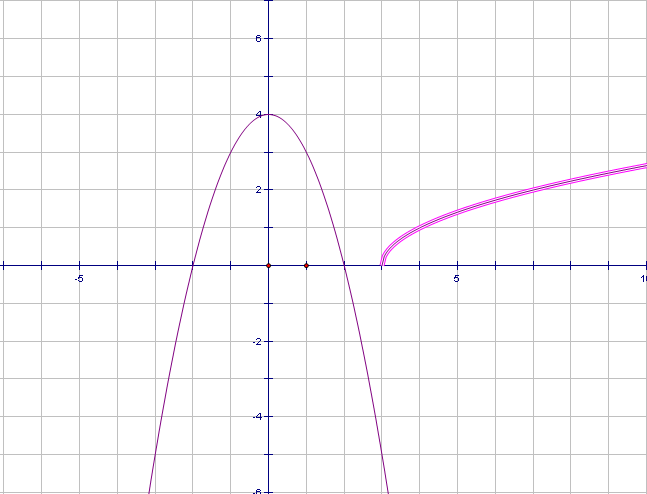
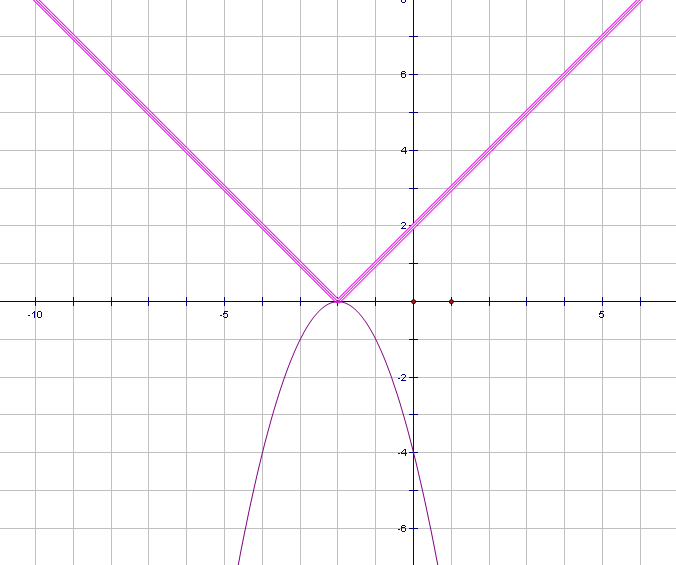
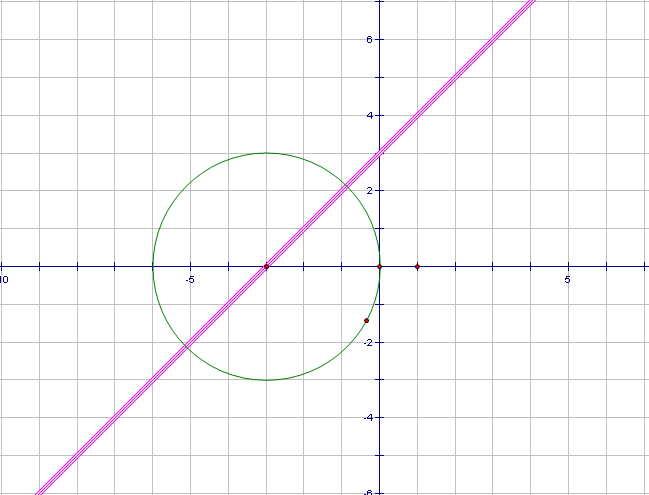
Задание2.На доске графики уравнений. Попробуйте узнать, графики каких функций изображены на рисунках и запишите решения данных систем уравнений.
Рис1
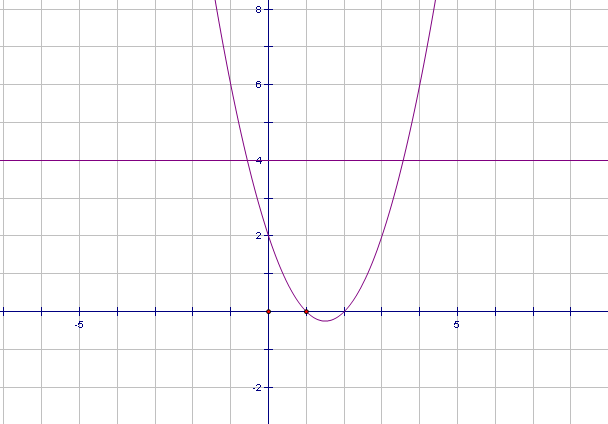
Рис.2
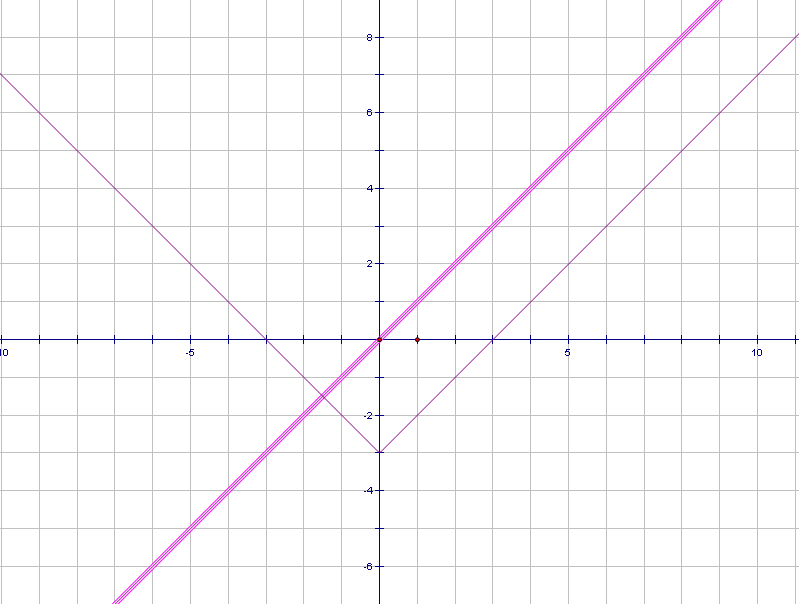
Рис.3
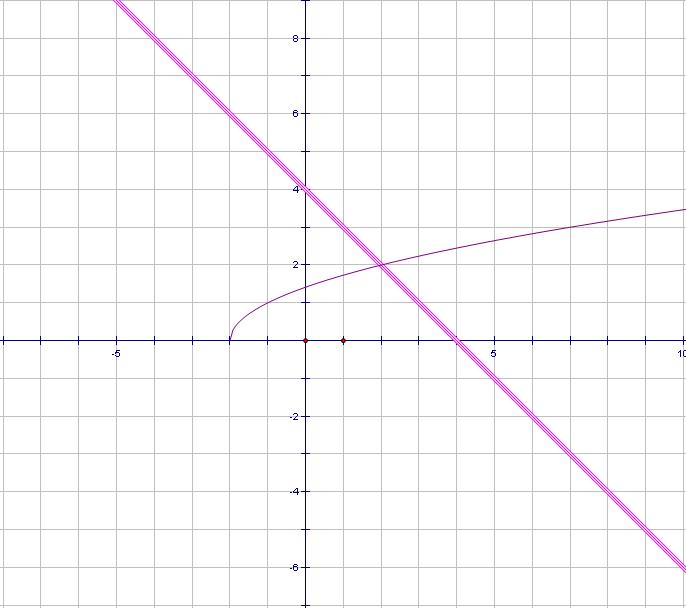
Рис.4
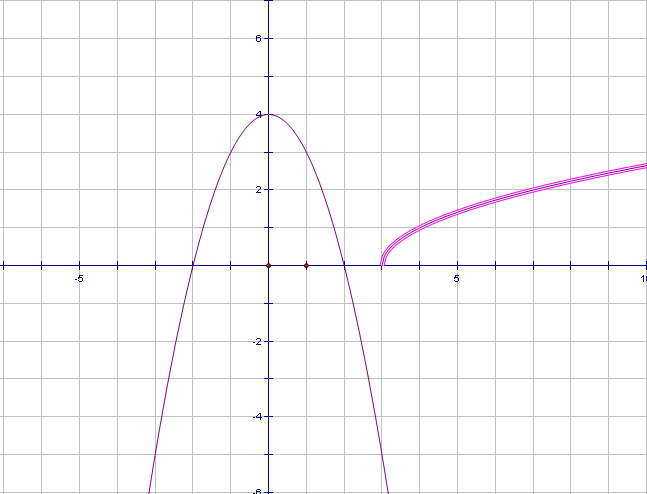
Рис.5
Рис.6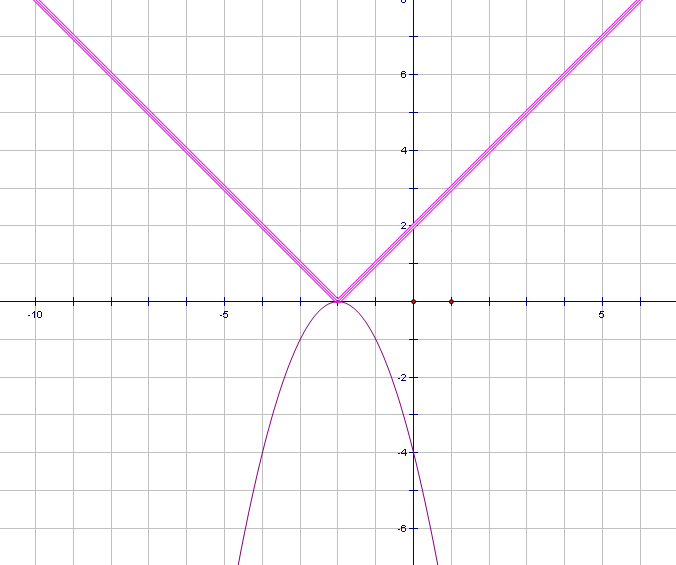
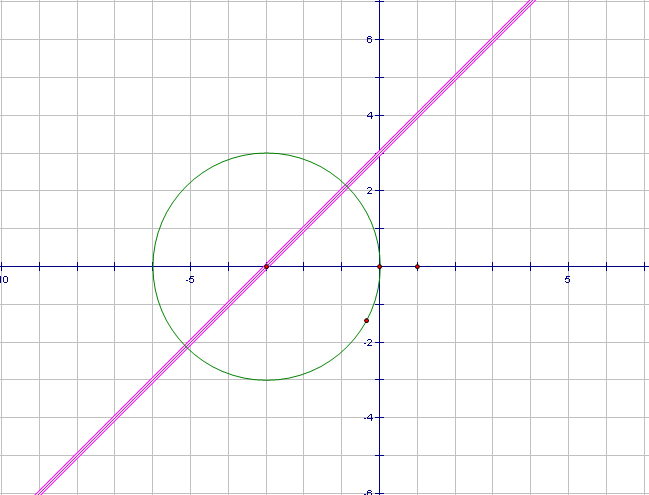
Проверка полученных результатов. (вызов учеников к доске и запись результатов). Графики каких уравнений вы здесь видите? (прямая, парабола, уравнение окружности, график уравнения модуля и у=�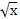 �). Какие сложности возникли при записи результатов? (сложно определить точные координаты).
�). Какие сложности возникли при записи результатов? (сложно определить точные координаты).
Вывод: (учащиеся делают самостоятельно)
Когда удобен графический способ решения систем уравнений? (когда после несложных преобразований уравнений системы можно без затруднений построить их графики.)
Что необходимо предпринять чтобы решить систему уравнений графически?
( 1) построить графики уравнений, входящих в систему в координатной плоскости; 2) найти точки пересечения этих графиков (это ответ на вопрос сколько решений имеет система уравнений) и определить их координаты; 3) найденные координаты точек пересечения проверить подстановкой в систему. )
Запись в тетради:
Решение систем уравнений графическим способом.
Алгоритм решения:
1) построить графики уравнений, входящих в систему в координатной плоскости;
2) найти точки пересечения этих графиков (это ответ на вопрос сколько решений имеет система уравнений) и определить их координаты;
3) найденные координаты точек пересечения проверить подстановкой в систему.
П

у
4
ример 1 (построение на интерактивной доске)
х
3
= -1 х  = -1
= -1
х 2 + у = 4 у = 4 - х2
2 + у = 4 у = 4 - х2
Н х
0
-1
У = 4 – х2
Х = -1
ашли точку пересечения х = -1
у = 3
подстановка:
х = -1
= -1
(-1)2 + 3 = 4
О твет: (-1; 3)
твет: (-1; 3)
В се последующие задания выполняются в тетради и на доске с вызовом учеников.
се последующие задания выполняются в тетради и на доске с вызовом учеников.
х 2 + у = 3 х 2 + у 2 = 1
2 + у = 3 х 2 + у 2 = 1
х – у + 1 = 0 у = �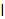 �х∣ - 1
�х∣ - 1
Ответ: (1; 2); (-2; -1) Ответ: (-1; 0); (0; -1); (1; 0)
(
 х -3)2 + (у + 1)2 = 9 у – х2 = 0
х -3)2 + (у + 1)2 = 9 у – х2 = 0
у = -1 у = �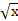 �
�
Ответ: (0; -1); (6; -1) Ответ: (0; 0); (1; 1)
П ри каком значении параметра р система уравнений имеет а) три решения?; б) одно решение?
ри каком значении параметра р система уравнений имеет а) три решения?; б) одно решение?
х2 + у2 = 4
у – х2 = р
Ответ: а) при р = -2; б) при р = 2.
Д/З
Сколько решений имеет система уравнений?
(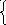
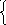 х +1)2 + (у + 2)2 = 4 х = 2
х +1)2 + (у + 2)2 = 4 х = 2
у = 0 (х +2)2 + (у - 2)2 = 16
2) Решить систему уравнений графически:
№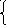 1 №2
1 №2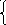
х2 - у = 3 (х + 2)2 + (у – 1)2 = 1
у = 6 у = �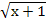 �
�
№3 №4
х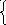
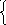 2 + у 2 = 4 х 2 + у 2 = 9
2 + у 2 = 4 х 2 + у 2 = 9
у = -0,5х2 + 2 у = �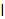 �х∣ - 3
�х∣ - 3
Работа в компьютерном классе:
Компьютерное обеспечение инженерных расчетов в пакете SCILAB
Методические указания к лабораторной работе №1
Цель работы:
ознакомится с простейшими действиями в среде SciLab;
ознакомится с построением графиков и графическим методом решения уравнений;
ознакомится с стандартными средствами решения уравнений в среде SciLab, сделать выводы о влиянии выбора начального значения;
ознакомится с языком программирования среды SciLab и редактором функций SciPad;
произвести математическое моделирование преобразования сигнала нелинейным элементом.
Выполнение
1.Запустите программу генерации заданий “lab2.exe” , после запуска вы увидите следующее окно
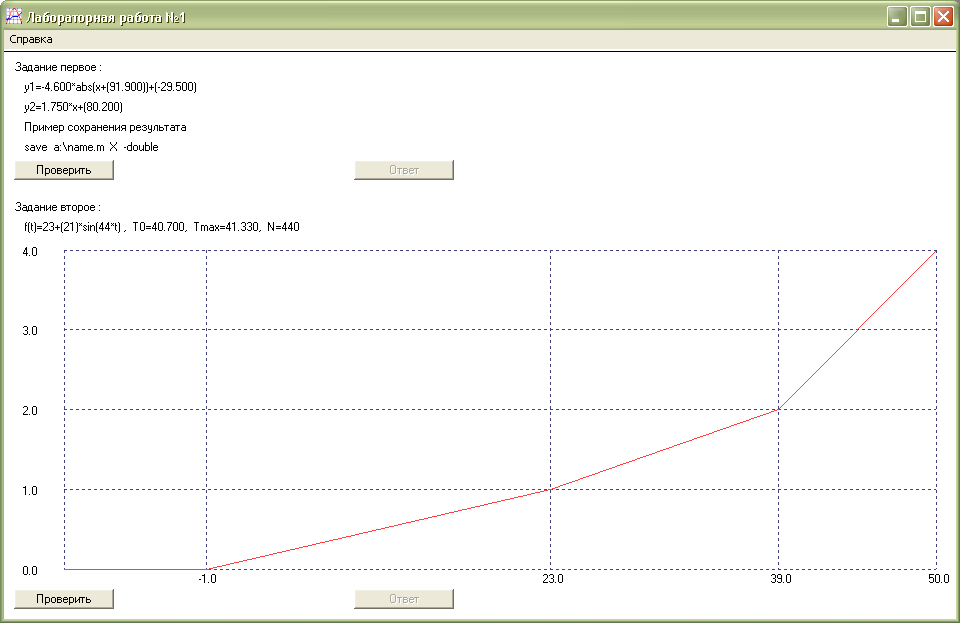
2.Запустите программу SciLab
1.Решение системы уравнений
Построим графики обоих уравнений системы на одной плоскости
Формируем массивы X,Y1,Y2 и функцией plot() строим графики Y1(x) и Y2(X)

2.Результат вызова функции plot()
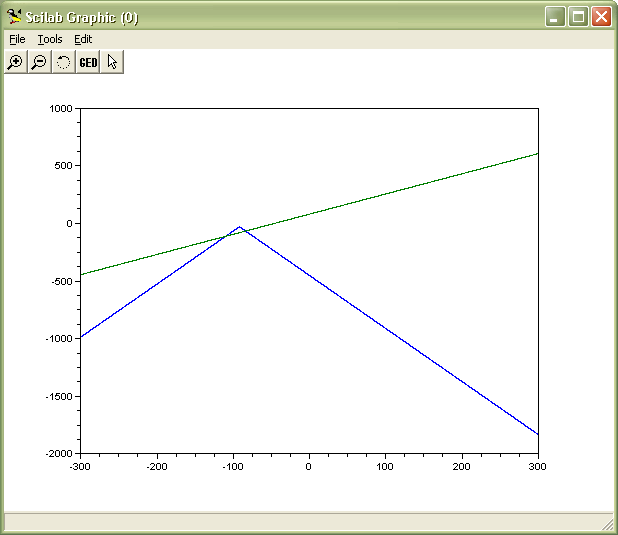
Определите примерные координаты x1,x2 точек пересечения (при необходимости возможно использовать увеличение)
Например, по приводимому графику
x1=-120
x2=-70;
3. Функция fsolve() определяет точку, в которой функция обращается в 0 (ноль), ближайшую к указанной.
При помощи функции deff() зададим функцию равную разности y1(x) и y2(x)
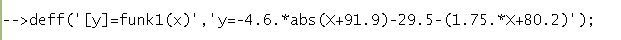
Создайте вектор ‘a’ для записи результата
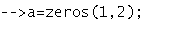
Ищем корни при помощи функции fsolve() последовательно подставляя в неё x1 и x2 из пункта 2
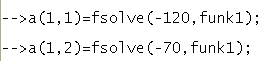
В результате массив результатов (содержащий значения x обоих решений системы уравнений) a будет такой:

Для того, чтобы увидеть значения y1 и y2 достаточно рассчитать значения y1 или y2, подставив вместо x имя матрицы а.
4.Сохраняем результат в файл и нажимаем кнопку “Проверить”, в открывшемся окне указываем путь к сохраненному файлу

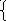
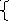 х2 + у2 = 1 а) (0; 1); б) (-1; -1); в) (1; 0) г) (1; 1)
х2 + у2 = 1 а) (0; 1); б) (-1; -1); в) (1; 0) г) (1; 1) 







 2 + у = 4 у = 4 - х2
2 + у = 4 у = 4 - х2  твет: (-1; 3)
твет: (-1; 3) се последующие задания выполняются в тетради и на доске с вызовом учеников.
се последующие задания выполняются в тетради и на доске с вызовом учеников.  2 + у = 3 х 2 + у 2 = 1
2 + у = 3 х 2 + у 2 = 1
 1 №2
1 №2



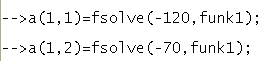

 х2 + у2 = 1 а) (0; 1); б) (-1; -1); в) (1; 0) г) (1; 1)
х2 + у2 = 1 а) (0; 1); б) (-1; -1); в) (1; 0) г) (1; 1) 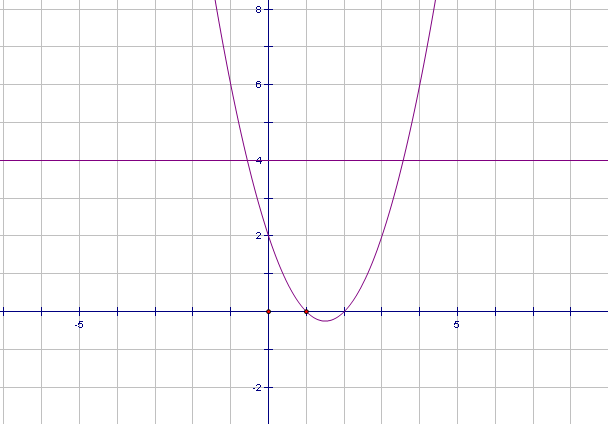
 1 №2
1 №2
 х -3)2 + (у + 1)2 = 9 у – х2 = 0
х -3)2 + (у + 1)2 = 9 у – х2 = 0 















