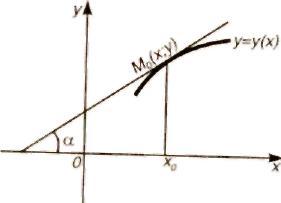
Поставим своей задачей определить скорость, с которой изменяется величина у в зависимости от изменения величины х. Так как нас интересуют всевозможные случаи, то мы не будем придавать определенного физического смысла зависимости y=f(x), т.е. будем рассматривать величины х и у как математические. Рассмотрим функцию y=f(x), непрерывную на отрезке [а, b]. Возьмем два числа на этом отрезке: х и х+?x; первое, х, в ходе всего рассуждения считаем неизменным, ?x — его приращением. Приращение ?x; аргумента обусловливает приращение ?у функции, причем: ?y=f(x+?x)-f(x). (I) Найдем отношение приращения ?у функции к приращению ?x аргумента: ?у/?x=(f(x+?x)-f(x))/ ?x. (II) По предыдущему, это отношение представляет собой среднюю скорость изменения у относительно х на отрезке [x, x+?x]. Будем теперь неограниченно приближать ?x к нулю. Для непрерывной функции f(x) стремление ?x к нулю вызывает стремление к нулю ?у, отношение (II) становится при этом отношением бесконечно малых, вообще величиной переменной. Пусть это переменное отношение (II) имеет вполне определенный предел(утверждать, что определенный предел отношения ?x/?у всегда существует нельзя), обозначим его символом f '(х).
lim((f(x+?x)-f(x))/ ?x)=f’(x)
?x→0
В данной работе представлена теория и приведены примеры решения задач на применение производной.