Конспект урока по теме "Геометрический смысл производной" предназначен для проведения урока в 11 классе, как подготовка к ЕГЭ заданий В8 и В14. Цель данного урока: выяснить в чем состоит геометрический смысл производной, уравнения касательной к графику функции, выработать практические навыки применения данного понятия в заданиях ЕГЭ. Урок сопровождается мультимидийной презентацией.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
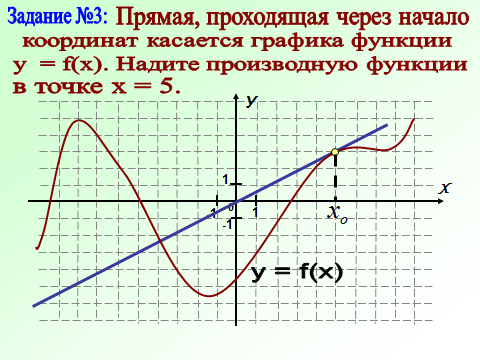
Геометрический смысл производной
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Геометрический смысл производной »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
2220 руб.
3170 руб.
2100 руб.
3000 руб.
2100 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
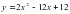
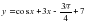
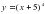
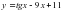
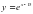
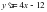
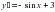
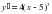
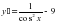
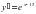
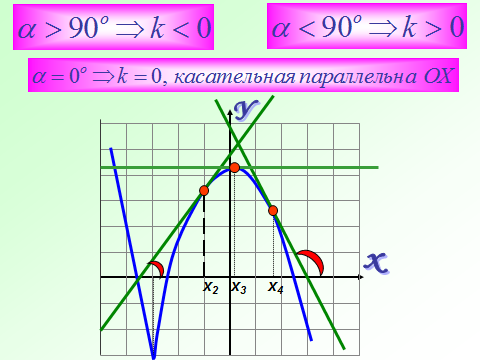
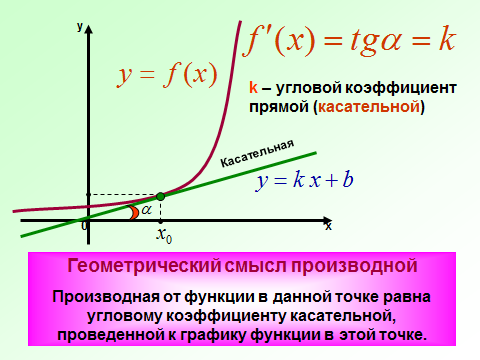 На этом рисунке мы видим график функции f(x) и в т.х0 к этому графику проведена касательная у=кх+в. Касательная образует с положительной осью Ох угол α. Касательная имеет угловой коэффициент к . Геометрический смысл производной заключается в том, что производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Кроме этого производная от функции в данной точке равна тангенсу угла наклона касательной с положительной осью Ох.
На этом рисунке мы видим график функции f(x) и в т.х0 к этому графику проведена касательная у=кх+в. Касательная образует с положительной осью Ох угол α. Касательная имеет угловой коэффициент к . Геометрический смысл производной заключается в том, что производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Кроме этого производная от функции в данной точке равна тангенсу угла наклона касательной с положительной осью Ох.