Батыс ?аза?стан облысы Теректі ауданы Абай аулы
Абай атында?ы жалпы орта білім беретін мектеп
Математика п?ніні? м??алімі: Са?ын?алиева С.Е.
Саба?ты? та?ырыбы: Функцияны зерттеу.
Саба?ты? ма?саты: І.Білімділік:
1.О?ушыларды функцияны? ?асиеттерін ?олдана отырып,функцияны зерттеуді ж?не зерттеу негізінде графигін салуды ?йрету.
ІІ.Дамытушылы?:
1.Осы та?ырып бойынша есептерді шы?ару,ж?мыс істеу да?дыларын дамыту.
2.О?ушыларды? іскерлік ?абілеттерін арттыру,шы?армашылы? ж?мыс істеуге баулу.
ІІІ.Т?рбиелік:
1.О?ушыларды? жауапкершілік сезімін арттыру,е?бектенуге т?рбиелеу.
Саба?ты? к?рнекілігі: слайдтар: ережелер, триггерлер
Саба?ты? ?дісі: жа?а саба? т?сіндіру:
Саба?ты? барысы:
І.?йымдастыру.
ІІ.?й тапсырмасын тексеру.
ІІІ.?тілген материал бойынша пысы?тау:
«Ой ?оз?ау». Слайд №2,3,4,5
1.Функцияны? аны?тамасы ?алай т?жырымдалады?
Х жиынында?ы х-ті? ?рбір м?ніне У жиыныны? на?ты бір у м?нін с?йкес ?оятын ереже немесе за?дылы? функция деп аталады.
Белгіленуі: y=f(х), y=g(х)
у-т?уелді айнымалы немесе аргумент
х-т?уелсіз айнымалы немесе функция
f.g-ереже немесе за?дылы?
2.Функцияны? аны?талу облысы дегеніміз не?
y=f(х) функциясы белгілі бір м?н ?абылдайтын т?уелсіз айнымалыны? на?ты м?ндер жиынын жиынын функцияны? аны?талу облысы деп атаймыз? D(f(х))
3.Функцияны? м?ндеріні? облысы дегеніміз не?
Аны?талу облысынан алын?ан ?рбір т?уелсіз айнымалы?а с?йкес табыл?ан функцияны? м?ндерін оны? м?ндер жиыны Е(f(х)) деп атайды.
4.Функцияны? берілуіні? ?андай т?сілдері бар?
1.Кестелік т?сіл. Ерекшелігі – аргументті? м?ндеріне с?йкес функцияны? м?ндері ?атар беріледі.
2.Графиктік т?сіл. Ерекшелігі – к?рнекілігінде.
3.Аналитикалы? т?сіл.Ерекшелігі: функцияны толы? зерттеуге ?олайлы.
5. ?андай функция ж?п функция деп аталады?
Егер y=f(х) функциясыны? аны?талу облысы симметриялы жиын болып, кез келген х аргументі ?шін f(-х)=f(х) те?дігі орындалса, онда функция ж?п деп аталады.Ж?п функцияны? графигі ординалар осіне ?ара?анда симметриялы.
6. ?андай функция та? функция деп аталады?
Егер y=f(х) функциясыны? аны?талу облысы симметриялы жиын болып, кез келген х аргументі ?шін f(-х)=-f(х) те?дігі орындалса, онда функция та? деп аталады.Та? функцияны? графигі координаталар басына ?ара?анда симметриялы.
7. ?андай функция периодты функция деп аталады?
Егер y=f(х) функциясы ?шін Т≠0 саны табылып ж?не аны?талу облысынан алын?ан кез келген х ?шін f(х+Т) = f(х) те?дігі орындалса, онда ол периодты функция деп аталады. Т≠0 саны функция периоды.
8.Функция та?басыны? т?ра?тылы? аралы?тары дегеніміз не?
Аны?талу облысыны? ?айсібір аралы?тарында функция тек о? м?ндерді (оны? графигі Ох осіні? жо?ар?ы жа?ындаорналас?ан), ал бас?а аралы?тарда тек теріс м?ндерді (график Ох осіні? т?менгі жа?ында орналас?ан) ?абылдаса, онда м?ндай аралы?тарды функция та?ба т?ра?тылы? аралы?тары деп атайды.
9. ?андай функцияны ?спелі, кемімелі функция деп атайды?
Егер у=f(х) функциясыны? Х жиынында?ы кез келген х?<х? сандары ?шін f (х?) <f(х?) те?сіздігі орындалса, онда функция ?спелі, ал f(х?) >f(х?) те?сіздігі орындалса, онда ол Х жиынында кемімелі деп аталады.
10. ?андай функцияны кемімейтін, ?спейтін функция деп атайды?
Егер у=f(х) функциясыны? Х жиынында?ы кез келген х?<х? сандары ?шін f (х?) £ f(х?) те?сіздігі орындалса, онда функция кемімейтін, ал f(х?) ³f(х?) те?сіздігі орындалса, онда ол Х жиынында ?спейтін функция деп аталады.
11.?андай н?ктені функцияны? минимум, максимум н?ктесі деп атайды?
Егер х? н?ктесіні? ?андай да бір айма?ынан алын?ан барлы? х (м?нда?ы х?≠х) ?шін f(х) >f(х?) те?сіздігі орындалса, онда х? н?ктесі f(х) функцияны? минимум, ал f(х) <f(х?) те?сіздігі орындалса, максимум н?ктесі деп аталады.
Тапсырма: Графикпен ж?мыс. (6,7слайд ар?ылы)
1. Берілген функцияны? аны?талу облысы ?андай аралы?та?
2.М?ндеріні? облысы?
3.Функция ж?п па, та? па?
4.Периодты ма?
5.График ?андай н?ктелерде координата осьтерімен ?иылысады?
6.Та?ба т?ра?тылы? аралы?тары?
7.?андай аралы?та ?седі, кемиді?
8.Экстремум н?ктелерін к?рсеті?дер.
І?.Жа?а саба?: 1. Функцияны зерттеу алгоритмі:
1)Функцияны? аны?талу облысын табу;
2) Функцияны? ж?п, та?ты?ын аны?тау. Егер функция ж?п не та? болса, онда аны?талу облысында?ы аргументті? тек о? м?ндер аралы?ында зерттеледі ж?не ж?п, та? функцияларды? графигі туралы ?асиет пайдаланылады;
3)Функцияны? периодтылы?ын аны?тау.Егер функция периодты болса, онда бір период аралы?ында ?ана зерттеледі;
4)Графикті? координаталар осьтерімен ?иылысу н?ктелерін табу;
5)Функция та?басыны? т?ра?тылы?, ?су, кему аралы?тарын, экстремум н?ктелерін табу, шектелгендігін аны?тау;
6) Аны?талу облысына кірмейтін н?ктелер айма?ында ж?не аргументті? модуль бойынша шексіз ?лкен м?ндерінде функцияны? ?згеру сипатын зерттеу;
7)Зерттеу н?тижелері бойынша график салу.
О?улы?тан 1,2мысал ?арастырамыз.
?.Дамыту кезе?і: Есептер шы?ару: О?улы?: №44(а,б), №45(а,б), №46(а,б)
VІ.Саба?ты бекіту: 1. №47 (а)
1.Функцияны? ?асиеттеріне не жатады?
2.Функцияны зерттеу алгоритмі не ?шін ?ажет? Жауабын т?сіндірі?дер.
VІІ.?йге тапсырма: №44(?,в), №45(?,в), №46(?,в), №47(?,б)
VІІІ.?орытынды.
Просмотр содержимого документа
«функ зерт»
10-сынып.Алгебра және анализ бастамалары.
Сабақтың тақырыбы: Функцияны зерттеу.
Сабақтың мақсаты: І.Білімділік:
1.Оқушыларды функцияның қасиеттерін қолдана отырып,функцияны зерттеуді және зерттеу негізінде графигін салуды үйрету.
ІІ.Дамытушылық:
1.Осы тақырып бойынша есептерді шығару,жұмыс істеу дағдыларын дамыту.
2.Оқушылардың іскерлік қабілеттерін арттыру,шығармашылық жұмыс істеуге баулу.
ІІІ.Тәрбиелік:
1.Оқушылардың жауапкершілік сезімін арттыру,еңбектенуге тәрбиелеу.
Сабақтың көрнекілігі: слайдтар: ережелер, триггерлер
Сабақтың әдісі: жаңа сабақ түсіндіру:
Сабақтың барысы:
І.Ұйымдастыру.
ІІ.Үй тапсырмасын тексеру.
ІІІ.Өтілген материал бойынша пысықтау:
«Ой қозғау». Слайд №2,3,4,5
1.Функцияның анықтамасы қалай тұжырымдалады?
Х жиынындағы х-тің әрбір мәніне У жиынының нақты бір у мәнін сәйкес қоятын ереже немесе заңдылық функция деп аталады.
Белгіленуі: y=f(х), y=g(х)
у-тәуелді айнымалы немесе аргумент
х-тәуелсіз айнымалы немесе функция
f.g-ереже немесе заңдылық
2.Функцияның анықталу облысы дегеніміз не?
y=f(х) функциясы белгілі бір мән қабылдайтын тәуелсіз айнымалының нақты мәндер жиынын жиынын функцияның анықталу облысы деп атаймыз? D(f(х))
3.Функцияның мәндерінің облысы дегеніміз не?
Анықталу облысынан алынған әрбір тәуелсіз айнымалыға сәйкес табылған функцияның мәндерін оның мәндер жиыны Е(f(х)) деп атайды.
4.Функцияның берілуінің қандай тәсілдері бар?
1.Кестелік тәсіл. Ерекшелігі – аргументтің мәндеріне сәйкес функцияның мәндері қатар беріледі.
2.Графиктік тәсіл. Ерекшелігі – көрнекілігінде.
3.Аналитикалық тәсіл.Ерекшелігі: функцияны толық зерттеуге қолайлы.
5. Қандай функция жұп функция деп аталады?
Егер y=f(х) функциясының анықталу облысы симметриялы жиын болып, кез келген х аргументі үшін f(-х)=f(х) теңдігі орындалса, онда функция жұп деп аталады.Жұп функцияның графигі ординалар осіне қарағанда симметриялы.
6. Қандай функция тақ функция деп аталады?
Егер y=f(х) функциясының анықталу облысы симметриялы жиын болып, кез келген х аргументі үшін f(-х)=-f(х) теңдігі орындалса, онда функция тақ деп аталады.Тақ функцияның графигі координаталар басына қарағанда симметриялы.
7. Қандай функция периодты функция деп аталады?
Егер y=f(х) функциясы үшін Т≠0 саны табылып және анықталу облысынан алынған кез келген х үшін f(х+Т) = f(х) теңдігі орындалса, онда ол периодты функция деп аталады. Т≠0 саны функция периоды.
8.Функция таңбасының тұрақтылық аралықтары дегеніміз не?
Анықталу облысының қайсібір аралықтарында функция тек оң мәндерді (оның графигі Ох осінің жоғарғы жағындаорналасқан), ал басқа аралықтарда тек теріс мәндерді (график Ох осінің төменгі жағында орналасқан) қабылдаса, онда мұндай аралықтарды функция таңба тұрақтылық аралықтары деп атайды.
9. Қандай функцияны өспелі, кемімелі функция деп атайды?
Егер у=f(х) функциясының Х жиынындағы кез келген х₁ₔ сандары үшін f (х₁) f(хₔ) теңсіздігі орындалса, онда функция өспелі, ал f(х₁) f(хₔ) теңсіздігі орындалса, онда ол Х жиынында кемімелі деп аталады.
10. Қандай функцияны кемімейтін, өспейтін функция деп атайды?
Егер у=f(х) функциясының Х жиынындағы кез келген х₁₁) £ f(хₔ) теңсіздігі орындалса, онда функция кемімейтін, ал f(х₁) ³f(хₔ) теңсіздігі орындалса, онда ол Х жиынында өспейтін функция деп аталады.
11.Қандай нүктені функцияның минимум, максимум нүктесі деп атайды?
Егер х₀ нүктесінің қандай да бір аймағынан алынған барлық х (мұндағы х₀≠х) үшін f(х) f(х₀) теңсіздігі орындалса, онда х₀ нүктесі f(х) функцияның минимум, ал f(х)
Тапсырма: Графикпен жұмыс. (6,7слайд арқылы)
1. Берілген функцияның анықталу облысы қандай аралықта?
2.Мәндерінің облысы?
3.Функция жұп па, тақ па?
4.Периодты ма?
5.График қандай нүктелерде координата осьтерімен қиылысады?
6.Таңба тұрақтылық аралықтары?
7.Қандай аралықта өседі, кемиді?
8.Экстремум нүктелерін көрсетіңдер.
ІҮ.Жаңа сабақ: 1. Функцияны зерттеу алгоритмі:
1)Функцияның анықталу облысын табу;
2) Функцияның жұп, тақтығын анықтау. Егер функция жұп не тақ болса, онда анықталу облысындағы аргументтің тек оң мәндер аралығында зерттеледі және жұп, тақ функциялардың графигі туралы қасиет пайдаланылады;
3)Функцияның периодтылығын анықтау.Егер функция периодты болса, онда бір период аралығында ғана зерттеледі;
4)Графиктің координаталар осьтерімен қиылысу нүктелерін табу;
5)Функция таңбасының тұрақтылық, өсу, кему аралықтарын, экстремум нүктелерін табу, шектелгендігін анықтау;
6) Анықталу облысына кірмейтін нүктелер аймағында және аргументтің модуль бойынша шексіз үлкен мәндерінде функцияның өзгеру сипатын зерттеу;
7)Зерттеу нәтижелері бойынша график салу.
Оқулықтан 1,2мысал қарастырамыз.
Ү.Дамыту кезеңі: Есептер шығару: Оқулық: №44(а,б), №45(а,б), №46(а,б)
VІ.Сабақты бекіту: 1. №47 (а)
1.Функцияның қасиеттеріне не жатады?
2.Функцияны зерттеу алгоритмі не үшін қажет? Жауабын түсіндіріңдер.
VІІ.Үйге тапсырма: №44(ә,в), №45(ә,в), №46(ә,в), №47(ә,б)
VІІІ.Қорытынды.
Абай атындағы жалпы орта білім беретін мектеп
Ашық сабақ тақырыбы:
Функцияны зерттеу
Сыныбы: 10
Математика пәнінің мұғалімі: Сағынғалиева С.Е.
2013-2014 оқу жылы
Просмотр содержимого презентации
«функцияны зерттеу»
Батыс Қазақстан облысы Теректі ауданы Абай аулы
Абай атында ғ ы жалпы орта білім беретін мектеп
Математика пәнінің мұғалімі: Сагингалиева Салтанат Есенгалиевна
- Функцияның анықтамасы қалай тұжырымдалады?
Х жиынындағы х-тің әрбір мәніне У жиынындағы нақты бір у-тің
мәні сәйкес келетін заңдылық немесе ереже функция деп аталады.
Белгіленуі: у f (х), у g (х), у (х)
У-тәуелді айнымалы немесе функция
Х-тәуелсіз айнымалы немесе аргумент
f , g , - ереже немесе заңдылық
2.Функцияның анықталу облысы дегеніміз не?
y =f (х) функциясы белгілі бір мән қабылдайтын тәуелсіз айнымалының нақты мәндер жиынын жиынын функцияның анықталу облысы деп атаймыз? D ( f (х))
3.Функцияның мәндерінің облысы дегеніміз не?
Анықталу облысынан алынған әрбір тәуелсіз айнымалыға сәйкес табылған функцияның мәндерін оның мәндер жиыны Е( f (х)) деп атайды.
4.Функцияның берілуінің қандай тәсілдері бар?
1.Кестелік тәсіл.
Ерекшелігі – аргументтің мәндеріне сәйкес функцияның мәндері қатар беріледі.
2.Графиктік тәсіл.
Ерекшелігі – көрнекілігінде.
3.Аналитикалық тәсіл.
Ерекшелігі: функцияны толық зерттеуге қолайлы.
5. Қандай функция жұп функция деп аталады?
Егер y =f (х) функциясының анықталу облысы симметриялы жиын болып, кез келген х аргументі үшін f (-х) =f (х) теңдігі орындалса, онда функция жұп деп аталады.
Жұп функцияның графигі ординалар осіне қарағанда симметриялы.
6. Қандай функция тақ функция деп аталады?
Егер y =f (х) функциясының анықталу облысы симметриялы жиын болып, кез келген х аргументі үшін f (-х) = - f (х) теңдігі орындалса, онда функция тақ деп аталады.
Тақ функцияның графигі координаталар басына қарағанда симметриялы.
7. Қандай функция периодты функция деп аталады?
Егер y =f (х) функциясы үшін Т≠0 саны табылып және анықталу облысынан алынған кез келген х үшін f (х+Т) = f (х) теңдігі орындалса, онда ол периодты функция деп аталады.
Т≠0 саны функция периоды.
f (х ₔ ) теңсіздігі орындалса, онда ол Х жиынында кемімелі деп аталады." width="640"
8.Функция таңбасының тұрақтылық аралықтары дегеніміз не?
Анықталу облысының қайсібір аралықтарында функция тек оң мәндерді
(оның графигі Ох осінің жоғарғы жағындаорналасқан), ал басқа
аралықтарда тек теріс мәндерді (график Ох осінің төменгі жағында
орналасқан) қабылдаса, онда мұндай аралықтарды функция таңба
тұрақтылық аралықтары деп атайды.
9. Қандай функцияны өспелі, кемімелі функция деп атайды?
Егер у= f (х) функциясының Х жиынындағы кез келген х₁ ₔ сандары
үшін f (х₁) f (х ₔ ) теңсіздігі орындалса, онда функция өспелі , ал f (х₁) f (х ₔ )
теңсіздігі орындалса, онда ол Х жиынында кемімелі деп аталады.
f (х₀ ) теңсіздігі орындалса, онда х₀ нүктесі f (х) функцияның минимум , ал f (х) f (х₀ ) теңсіздігі орындалса, максимум нүктесі деп аталады." width="640"
10. Қандай функцияны кемімейтін, өспейтін функция деп атайды?
Егер у= f (х) функциясының Х жиынындағы кез келген х₁ ₔ сандары
үшін f (х₁) f (х ₔ ) теңсіздігі орындалса, онда функция кемімейтін , ал f (х₁) f (х ₔ )
теңсіздігі орындалса, онда ол Х жиынында өспейтін функция деп аталады.
11.Қандай нүктені функцияның минимум, максимум нүктесі деп атайды?
Егер х₀ нүктесінің қандай да бір аймағынан алынған барлық х (мұндағы
х₀≠х) үшін f (х) f (х₀ ) теңсіздігі орындалса, онда х₀ нүктесі f (х) функцияның
минимум , ал f (х) f (х₀ ) теңсіздігі орындалса, максимум нүктесі деп аталады.
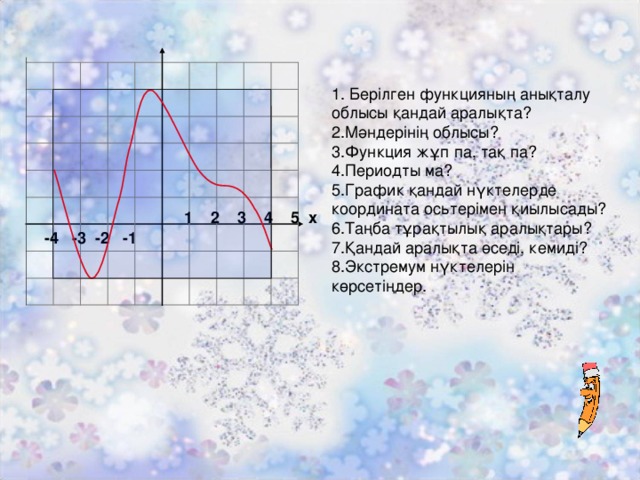
1. Берілген функцияның анықталу облысы қандай аралықта?
2.Мәндерінің облысы?
3.Функция жұп па, тақ па?
4.Периодты ма?
5.График қандай нүктелерде координата осьтерімен қиылысады?
6.Таңба тұрақтылық аралықтары?
7.Қандай аралықта өседі, кемиді?
8.Экстремум нүктелерін көрсетіңдер.
1 2 3 4 5 х
-4 -3 -2 -1
Функцияны зерттеу алгоритмі:
1)Функцияның анықталу облысын табу;
2) Функцияның жұп, тақтығын анықтау. Егер функция жұп не
тақ болса, онда анықталу облысындағы аргументтің тек оң мәндер аралығында зерттеледі және жұп, тақ функциялардың графигі туралы қасиет пайдаланылады;
3)Функцияның периодтылығын анықтау.Егер функция периодты болса, онда бір период аралығында ғана зерттеледі;
4)Графиктің координаталар осьтерімен қиылысу нүктелерін табу;
5)Функция таңбасының тұрақтылық, өсу, кему аралықтарын, экстремум нүктелерін табу, шектелгендігін анықтау;
6) Анықталу облысына кірмейтін нүктелер аймағында және аргументтің модуль бойынша шексіз үлкен мәндерінде функцияның өзгеру сипатын зерттеу;
7)Зерттеу нәтижелері бойынша график салу.
Оқулықпен жұмыс:
№ 44; №45
№ 46 (а,ә) №47 (а)
Үйге тапсырма: №46 (б,в) №47 (ә,б)
