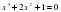Технологическая карта урока.
Технологическая карта урока математики.
Учитель: Пичугина Любовь Степановна, учитель математики МОУ ООШ№3 г. Камешково.
УМК: Алгебра 9класс: учеб. для ОУ /под ред. С.А. Теляковского-М- Просвещение, 2010.
Тема урока: Решение биквадратных уравнений.
Тип урока: урок открытия нового знания.
Цель урока: Организовать деятельность учащихся по получению знаний, приобретению умений и навыков и усвоению нового способа действия ( ие новой переменной).
Задачи урока, направленные на развитие учащихся
В личностном направлении :-развитие мотивации достижения и готовности преодоления трудностей
-умение преодоления трудностей
В метапредметном направлении: -развитие умений оценивать правильность выполнения учебной задачи;
-развитие умений классифицировать, самостоятельно выбирать критерии для классификации,, строить логическое рассуждение, умозаключение и делать выводы;
- развитие умений работать в парах.
В предметном направлении: - овладеть алгоритмом решения биквадратных уравнений.
Оборудование: проектор, маркерная доска.
Дидактическая структура урока
Деятельность учителя
Деятельность обучающихся
УУД
Время
Самоопределение к деятельности
Слайд 2.-Исторические сведения «Математик Вальмес и уравнения 4 степени». (приложение 1)
-Умеете ли вы решать уравнения 4 степени?
-Слушают учителя и подготавливаются к получению новых знаний.
-Отвечают на вопрос.
Личностные: мотивация учения
1-2
Актуализация знаний
Слайд 3. На слайде написаны уравнения 4 степени. Систематизированы в 4 группы. Нужно определить какие уравнения находятся в группах, если в каждой группе их различное количество: в I- одно, воII-два и т.д. Если никто из учеников не предложил классификацию по способу решения, то предлагает учитель. (приложение 2)
Учащиеся классифицируют уравнения, объясняют свой выбор.
Приходят к выводу, что они не умеют решать уравнение из 1 группы.
Познавательные: анализ, классификация, выдвижение гипотез и их обоснование.
4-5
Постановка учебной задачи
Слайд 4.- Предлагается тестовое задание. (Приложение 3).
-предлагает ученикам сформулировать тему и цель урока. Корректирует предложенные формулировки.
Слайд 5.
-Решая тестовое задание, делают вывод, что уравнение из 1 группы называется биквадратным.
-Дают определение биквадратного уравнения.
-Формулируют тему урока: биквадратные уравнения. Цель: составить алгоритм решения биквадратных уравнений.
Познавательные: подведение под понятие, поиск и выделение информации, формулирование познавательной цели.
4
Открытие нового знания
Слайд 6.- обучающимся предлагается алгоритм решения биквадратного уравнения из 7 пунктов. Но учитель перепутал пункты. Восстановите алгоритм.
Учащиеся в парах составляют алгоритм решения биквадратного уравнения.
Коммуникативные: контролирование действия партнёра, умение договорится и приходить к общему решению в совместной деятельности, умение выражать свои мысли.
Регулятивные: умение составлять план действий.
4
Первичное закрепление во внешней речи
Решить биквадратное уравнение.
Учитель оказывает помощь в записи решения уравнения
1 ученик, используя алгоритм, решает уравнение на доске. Комментирует свои действия. Показывает образец решения. Остальные записывают в тетради.
Регулятивные: алгоритмизация действий
6
Включение в систему знаний
Слайд 7. Лабораторная мини-работа. Цель: выяснить, сколько корней может иметь биквадратное уравнение? (Приложение 4)
Дифференцированные дополнительные задания. (Приложение 5)
Учащиеся работают в парах. Заполняют таблицу. Делают выводы.
Коммуникативные: контролирование действия партнёра, умение договорится и приходить к общему решению в совместной деятельности.
15
Домашнее задание
№278,
Слайд 8.
Ученики записывают домашнее задание.
1
Рефлексия
Слайд 9.Предлагает оценить свою работу (Приложение 6)
Регулятивные: умение оценивать свои достижения. Личностные: стремление к саморазвитию. достижения
3
Приложение1.
В 1487г. решением испанской инквизиции в г. Толедо был сожжён математик Паоло Вальмес
До казни учёный встретился у общих знакомых с инквизитором Томaс де Торквемада .
Торквемада высказал мысль, что решение уравнения 4-й степени самим богом спрятано и эту тайну никому не удастся открыть. Паоло Вальмес неосторожно рассказал, что он уже нашёл способ решения уравнений 4-й степени.
Через некоторое время Вальмеса арестовали и обвинили в содружестве с дьяволом. Через 3 недели ареста и жестоких истязанмй Паоло Вальмеса сожгли.
Приложение 2.
4) 1)
8)
5)
6)
9)
10)
3)
7)
2)
1)
2)
3)
4)
5)
6) I II III IV
7)
8)
9)
10)
II, III, IV-при решении применяется свойство произведения с 0. IV-способ разложения на множители ( вынесение за скобку общего множителя). III-…(группировка). II-…(формула сокращенного умножения) или
Приложение 3.
Данное уравнение называется а) линейное б)квадратное в) биквадратное г) дробное рациональное.
Определение: уравнения вида, где а , являющиеся квадратными относительно х2, называются биквадратными.
Приложение 4.
Алгоритм решения биквадратного уравнения. Метод решения - замены переменной.
I.Ввести замену переменной: пусть х2 = t.
II.Решить получившиеся квадратные уравнения. (одно, два или ни одного)
III.Составить квадратное уравнение с новой переменной:
- (2)
IV.Вернуться к замене переменной.
V.Решить новое квадратное уравнение (2).
VI.Записать ответ.
1. I. Ввести замену переменной: пусть х2 = t,
2. III.Составить квадратное уравнение с новой переменной:
аt2 + bt + с = 0 (2)
3. V. Решить новое квадратное уравнение (2).
4. IV.Вернуться к замене переменной.
5. II.Решить получившиеся квадратные уравнения. (одно, два или ни одного)
6. VI.Записать ответ.
х4=(х2)2=t2
х2 = t
D=1
t1=4 t2=5
х2 = 4 х2 = 5
х1=2 ; х2= –2 х3= ; х2= –
Ответ: – ; –2; 2;
Приложение 5.
Решите биквадратные уравнения и заполните таблицу для исследования числа решения биквадратных уравнений
1вариант.
1. ; 2. ; 3. ; 4.
Уравнение №4 можно решать не используя алгоритм.
2 вариант.
1. ; 2. ; 3. ; 4.
№
Уравнение
D
Корни промежуточного (нового) уравнения t1 и t2
Корни данного биквадратного уравнения
Количество решений биквадрат. уравнения
D=1
t1= 4 t2= 5
– ; –2; 2;
4
1
1в.
2в.
D=169
t1= 9 t2= –4
t1= 4 t2= –9
–3; 3
–2; 2
2
2
2
1в.
2в.
D= –19
Корней нет
Корней нет
Корней нет
Корней нет
0
0
3
1в.
2в.
D=0
t=1
t= –1
–1; 1
Корней нет
2
0
4
1в.
2в.
D=256
t1=0 и t2= –16
t1=0 и t2= 16
0
0; –4; 4
1
3
Вопрос. Как можно решит уравнение №3, не используя алгоритм.
Доп. задание. ( на выбор) или
D=64; t1= 1, t2= t1= 16, t2=
Ответ: –1; 1; ; Ответ: –4; 4; ; –
Приложение 6. Учитель предлагает оценить себя, ответив на вопросы.
1.Как вы поняли определение биквадратного уравнения.
2.Во всех ли случаях вы можете из предложенных уравнений выбрать биквадратное.
3.Как хорошо вы научились решать биквадратные уравнения?
4.Оцените работу в парах
5.Оцените комфорт на уроке.
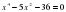 ; 2.
; 2.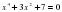 ; 3.
; 3. 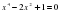 ; 4.
; 4.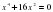
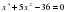 ; 2.
; 2.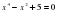 ; 3.
; 3.  ; 4.
; 4.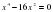
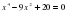
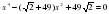
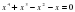
 1)
1)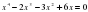
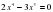


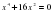
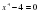
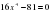

 , где а
, где а , являющиеся квадратными относительно х2, называются биквадратными.
, являющиеся квадратными относительно х2, называются биквадратными.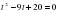
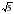 ; х2= –
; х2= – ; 2.
; 2.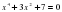 ; 3.
; 3. 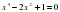 ; 4.
; 4.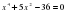
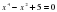 ; 3.
; 3.