Суходольский горный профессиональный лицей

(АЛГЕБРА И ИНФОРМАТИКА)
ТЕМА. РЯДЫ РАЗЛОЖЕНИЯ. МОДА И МЕДИАНА. СРЕДНИЕ ЗНАЧЕНИЯ.
ПОСТРОЕНИЕ ГРАФИКОВ НА ОСНОВЕ ТАБЛИЧНЫХ ДАННЫХ В СРЕДЕ ТАБЛИЧНОГО ПРОЦЕССОРА

Разработал:
преподаватель математики
высшей категории
Соболева Е. И.
:::
БИНАРНЫЙ УРОК (АЛГЕБРА И ИНФОРМАТИКА)
ТЕМА. Ряды разложения. Мода и медиана. Средние значения Обработка данных с помощью табличного процессора. Построение
графиков на основе табличных данных в среде табличного процессора.
ЦЕЛЬ. Дать понятие ряда разложения и его основных характеристик.
Рассмотреть наглядное представление вариационных рядов.
Изучить меры центральной тенденции: моду, медиану, среднее
арифметическое и среднее квадратичное рядов разложения.
Сформировать навыки работы по построению вариационных рядов и
выполнению вычислений на компьютере в среде табличного
процессора.
Формирование и активизация познавательной деятельности учащихся.
Привитие интереса к изучению предметов математика и информатика.
Контроль усвоения материала с помощью компьютера.
ТИП УРОКА. Урок усвоения новых знаний и навыков работы на компьютере.
СТРУКТУРА УРОКА
Организационный момент
Изучение нового материала (презентация)
Закрепление изученного материала (тестовые задания)
Повторение основных сведений по информатике
Выполнение практического задания
Подведение итогов
1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ
2. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА (презентация)
РЯДОМ РАЗЛОЖЕНИЯ называется ряд чисел, которые характеризуют разложение единиц исследуемой совокупности.
Если разложение единиц совокупности зависит от величины признака, то такой ряд называется ВАРИАЦИОННЫМ.
Изменение этого признака называется ВАРИАЦИЕЙ, а значение признака у данного члена статистической совокупности называется ВАРИАНТОЙ.
Если группирование вариант идет по отдельным значениям признака, то такое группирование называется ДИСКРЕТНЫМ (раздельным или прерывным).
Например: учащиеся группы получили на экзаменах такое количество баллов
(30 учащихся)
| Количество баллов | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8
| 9 | 10 | 11 | 12 |
| Количество учащихся | - | 1 | 2 | 13 | 6 | 2 | 1 | 2
| 2 | 1 | - | 1 |
Если группирование осуществляется по интервалам изменения признака, то такое группирование называется ИНТЕРВАЛЬНЫМ.
Например: выборочное измерение урожайности пшеницы на площади 1200га
дало следующие результаты
| Урожайность, Ц./га | 21-23 | 23-25 | 25-27 | 27-29 | 31-33 | 33-35
| Всего |
| Площадь, га | 100 | 150 | 250 | 300 | 250 | 150
| 1200 |
ЧАСТОТОЙ значения признака или интервала называется количество членов совокупности с некоторой вариантой или количество членов совокупности, варианты которых лежат в данном интервале.
Например: при дискретном группировании частота результата 8 баллов равна
2, а при интервальном группировании частота урожайности 25-27
Ц. / га равна 250.
Мода, медиана и средние значения называются мерами центральной тенденции.
Для наглядного изображения статистического разложения пользуются графическими изображениями – диаграммами, графиками, полигонами, гистограммами и т.п.
Примеры графических изображений статистических разложений
У




 0 1 8 13 21 29 х
0 1 8 13 21 29 х
ГИСТОГРАММА – это последовательность столбцов, каждый из которых опирается на один разрядный интервал, а высота отображает количество частот в этом разряде.
Принято расширять шкалу на один разрядный интервал влево и вправо. Применяется в основном при интервальном группировании.
ПОЛИГОН заканчивается точкой в середине интервала при интервальном группировании. Если группирование дискретное, то полигон напоминает график, только линии прямые и фигура замкнутая.
Т.о. свойства совокупности данных можно представлять в виде таблиц и графиков, но существуют еще такие характеристики рядов, как мода, медиана и средние значения: среднее арифметическое, среднее геометрическое и среднее квадратичное.
МОДА – это значение признака, который наиболее часто встречается в данном ряду разложения.
На примере сдачи экзамена Мо=4, т.к. 4 балла встречается 13 раз. Если у нас все значения встречаются одинаковое число раз, то моды нет.
Если два соседних значения имеют одинаковую частоту, то мода равна среднему значению.
Например: 1,2,3,3,4,4,5
Мо = 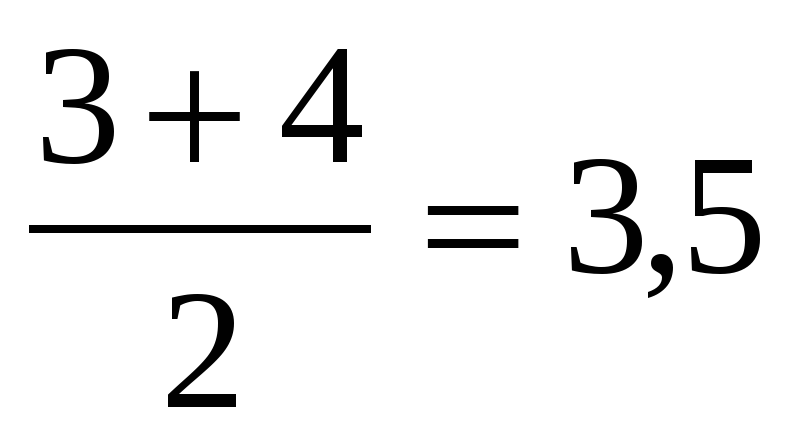
Если два несоседних значения имеют одинаковую большую частоту, то будет две моды
Например: 1,2,2,2,3,3,4,4,5,6,6,6,7
Мо =2 и 6
МЕДИАНА – среднее значение переменного признака, которое расположено в середине ряда, составленного в порядке возрастания или убывания.
Если число членов четное, то медиана – среднее значение между двумя центральными, если число членов ряда разложения – нечетное, то медиана – центральное значение.
Например: 2,4,7,7,8,9.10,12,13,14 2,4,7,7,8,9,10,12,13
Ме = 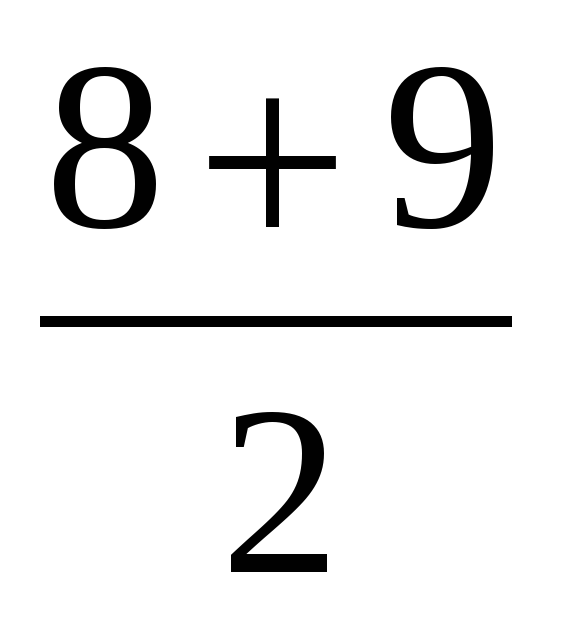 =8,5 Ме = 8
=8,5 Ме = 8
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ – это такое Х = (х +х
+х +…+х
+…+х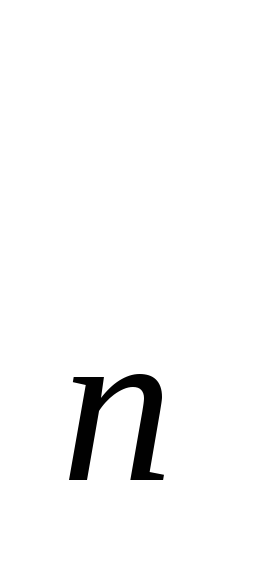 )/п или
)/п или
Х =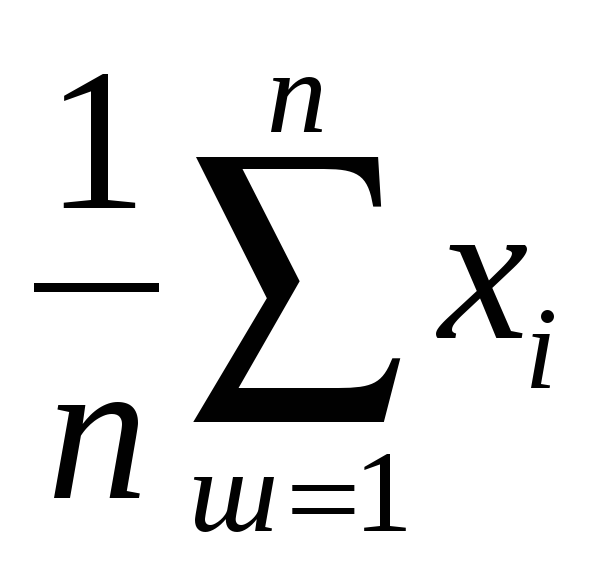
СРЕДНЕЕ КВАДРАТИЧНОЕ
 , где i=1,2,…
, где i=1,2,… п
п
СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ
m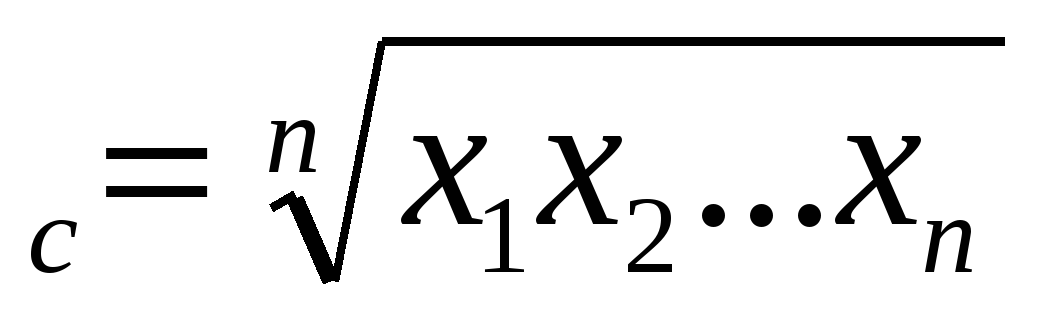

3. ТЕСТОВОЕ ЗАДАНИЕ (выполняется на компьютере)
Значение признака – это
А) частота
Б) варианта
В) вариация
Г) мода
Последовательность столбцов – это
А) график
Б) диаграмма
В) гистограмма
Г) полигон
Среднее квадратичное обозначается буквой
А) 
Б) Х
В) m
Г) Ме
Дан ряд чисел 2,4,6,5,4,2,4,1,8. Найти моду
А) 4
Б) 2
В) 2, 4
Г) нет моды
5. Дан ряд чисел 2,2,4,4,5,5,6,6,7,7. Чему равна мода?
А) 5
Б) 2,4,5,6,7
В) нет моды
Г) 4 и 5
6.В данном ряду чисел указать медиану
1,2,2,3,4,5,5,6,7
А) 2
Б) 4
В) 5
Г) 2 и 5
Что не является мерой центральной тенденции?
А) мода
Б) медиана
В) варианта
Г) среднее арифметическое
Среднее значение ряда является медианой, если ряд содержит
А) четное число единиц
Б) нечетное число единиц
В) любое количество единиц
Г) не содержит ни одного элемента
Буквой Х обозначается
А) медиана
Б) среднее арифметическое
В) среднее квадратичное
Г) среднее геометрическое
При графическом изображении интервального вариационного ряда обычно используется
А) гистограмма
Б) диаграмма
В) полигон
Г) график
4. АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ
Как называется табличный процессор
Как производится ввод данных в таблицу
Где расположена строка меню
Какая клетка называется активной
5. ПРАКТИЧЕСКАЯ ЧАСТЬ (выполняется на ПК в среде табличного редактора)
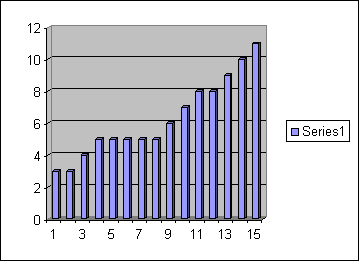
Задание. Построить дискретный вариационный ряд, найти моду, медиану, среднее арифметическое, среднее геометрическое, построить гистограмму данного ряда, если при сдаче экзамена 15 учащиеся получили следующее количество баллов׃
5,3,8,5,7,5,4,10,9,8,5,11,3,5,6
6.ПОДВЕДЕНИЕ ИТОГОВ
ИНСТРУКЦИЯ ПО ВЫПОЛНЕНИЮ ВЫЧИСЛЕНИЙ И ПОСТРОЕНИЮ ГРАФИКОВ В СРЕДЕ ТАБЛИЧНОГО ПРОЦЕССОРА
Войти в табличный процессор, выбрав программу Microsoft Excel
Выделить клетку в столбце В
Внести данные в столбец
Расположить данные в порядке возрастания, для этого обвести данные и произвести следующие действия / данные / сортировка / столбец по возрастанию/ ОК
Найти моду, медиану, среднее арифметическое и среднее геометрическое построенного дискретного вариационного ряда.
Для вычисления произвести следующие действия – выделить клеточку, вписать название характеристики, выделить напротив характеристики еще одну клеточку, войти в меню / вставка / функция / статистические / название необходимой характеристики / ОК
После появления диалогового окна, выделить столбец чисел. В диалоговом окне появляются параметры ряда. Нажав ОК, получаем необходимый результат.
Аналогично находим все характеристики.
Для построения графика производим следующие действия – выделить данные
/ вставка / диаграмма / гистограмма /, выделяем необходимый вид гистограммы
/ готово /
| 3 |
| мода |
| 5 | 
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
| 4 |
| медиана |
| 5 |
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
| 5 |
| ср.арифм. | 6,266667 |
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
| 5 |
| ср.геом. |
| 5,82212 |
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
|
|
|
|
|
| 10 |
|
|
|
|
|
|
|
|
|
|
|
| 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|