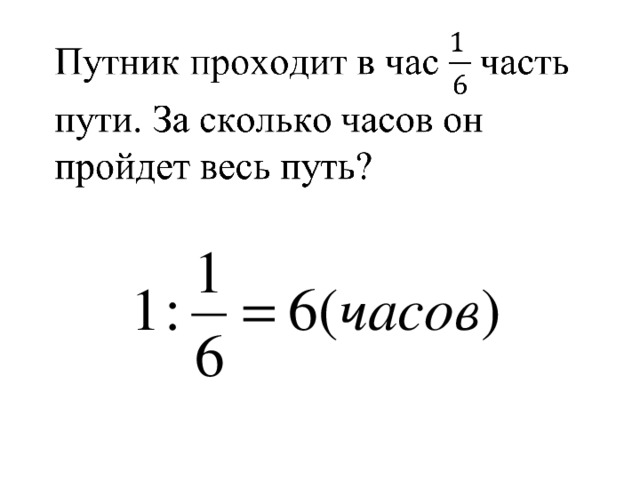Сценарий урока математики в 6 классе
| Организационная информация |
| Предмет | Математика |
| Класс | 6 |
| Рабочая программа педагога | Курс «Математика. Решение задач» (35 часов). |
| Тема урока | Решение задач на совместную работу |
| Автор урока (ФИО, должность) | Евсеева Елена Михайловна, учитель математики |
| Образовательное учреждение | МОУ «СОШ с. Липовка Духовницкого района Саратовской области» |
| Федеральный округ России | Приволжский федеральный округ |
| Республика/край /область | Саратовская область |
| Район | Духовницкий район |
| Город/поселение | с. Липовка |
|
|
| Методическая информация |
| Тип урока | Урок «открытия» нового знания |
| Цель урока | Научиться решать задачи на совместную работу |
| Задачи урока | 1. Дидактическая: - ознакомить учащихся с решением задач на совместную работу арифметическим способом; - повторить и закрепить действия с обыкновенными дробями и рациональными числами; - показать прикладную значимость математики в практической деятельности. 2. Развивающая: - развивать грамотную математическую речь и активизировать мыслительную деятельность; - развивать умение рассуждать и делать выводы. 3. Воспитательная: - развивать внимание, умение выслушивать мнение товарищей. |
| Используемые педагогические технологии, методы и приемы | Элементы информационно-коммуникационных технологий, игровых технологий. |
| Время реализации урока | 45 минут |
| Необходимое оборудование и материалы | 1. компьютер с подключением к Интернету; 2. колонки; 3. медиа проектор; 4. экран; 5. компьютерная мышь;
|
Ход урока:
1. Организационный момент
2. Постановка целей и задач урока
Сегодня на уроке мы продолжим отрабатывать навыки решения текстовых задач арифметическим способом; решение исторических задач и старинных способов их решения расширит представление о практике решения задач в старые времена. Слайд № 1
3. Устная работа Слайд № 2 – 7.
1. Бассейн наполняется за 3 ч. Какая часть бассейна наполняется за 1 ч?
Решение:
1: 3 = 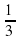 часть бассейна наполнится за 1 час.
часть бассейна наполнится за 1 час.
Ответ: 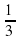
2. Работу выполнили за 5 часов. Какую часть работы выполняли в каждый час?
Решение:
1 : 5 = 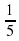 часть работы выполняли каждый час.
часть работы выполняли каждый час.
Ответ: 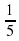
3. В каждый час труба наполняет 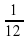 часть бассейна. За сколько часов она наполнит бассейн?
часть бассейна. За сколько часов она наполнит бассейн?
Решение:
1: 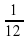 = 12 часов – время для наполнения бассейна.
= 12 часов – время для наполнения бассейна.
Ответ: 12 часов.
4. Путник проходит в час 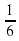 часть пути. За сколько часов он пройдет весь путь?
часть пути. За сколько часов он пройдет весь путь?
Решение:
1 : 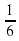 = 6 часов затратит путник на весь путь.
= 6 часов затратит путник на весь путь.
Ответ: 6 ч.
5. В каждый час первая труба наполняет 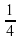 бассейна, а вторая –
бассейна, а вторая – 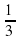 бассейна. Какую часть бассейна наполняют обе трубы за 1 час совместной работы.
бассейна. Какую часть бассейна наполняют обе трубы за 1 час совместной работы.
Решение:
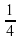 +
+ 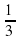 =
= 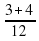 =
= 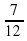 (часть бассейна) – наполняют обе трубы за 1 час
(часть бассейна) – наполняют обе трубы за 1 час
Ответ: 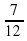
6. Два путника одновременно вышли навстречу друг другу и встретились через 3 часа. На какую часть первоначального расстояния они сближались в каждый час?
Решение:
1 : 3 = 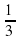 часть расстояния соответствует сближению путников за час.
часть расстояния соответствует сближению путников за час.
Ответ: 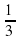 .
.
4. Проверка домашнего задания
Учащиеся должны были придумать сами или подобрать из различных источников
опорные задачи на совместную работу.
https://www.youtube.com/watch?v=8xBrZN1kth0
http://yandex.ru/video/search?text=видео%20задачи%20на%20совместную%20работу%205%20класс&path=wizard&parent-reqid=1461165924276691-1743190154922036750821977-man1-2960&filmId=ZzSqY0tKUXI
5. «Открытие» детьми нового знания. Способы действия в новой ситуации
Учитель: Хорошо. Все успешно справились с предложенным заданием, а теперь прошу все внимание на доску. Мы начинаем изучать новую тему, которая называется «Задачи на совместную работу».
Сегодня на уроке мы научимся решать новые задачи на совместную работу, опираясь на усвоенные методы решения опорных задач.
Хочу напомнить, что всю работу принято считать равной единице и при этом всё равно, какую работу выполняют и в чём её измеряют.
Рассмотрим старинную задачу из математической рукописи XVII века: « Два плотника рядились двор ставить. И говорит первый - Только бы мне одному двор ставить, то я бы поставил за 3 года.
А другой молвил:
- Я бы поставил его в шесть лет.
Оба решили сообща ставить двор. Сколько долго они ставили двор?»
Что надо найти в задаче? Давайте ответим на вопрос задачи.
(Предполагаемый ответ: Время, за которое два плотника поставят двор, если будут работать сообща.)
Но как найти его?
(Предполагаемые ответы: 1) плотники вместе будут строить двор 3 + 6 = 9 лет
2) вместе плотники должны построить двор быстрее, а не дольше, чем каждый из них в отдельности.
3) время совместной работы не может быть больше трех лет.)
Кто нам подскажет алгоритм решения данной задачи?
Затрудняетесь?
Почему вы не смогли решить задачу?
(Предполагаемый ответ: Это новый для нас тип задач.)
Как мы назовем такие задачи?
(Предполагаемый ответ: Задачи на совместную работу).
Сформулируйте тему урока.
Запишите тему урока: Задачи на совместную работу.
Какую задачу мы поставим перед собой?
(Предполагаемый ответ: Составить алгоритм решения задач на совместную работу и научиться использовать его при решении задач) Давайте вернемся к нашей задаче и решим ее?
Для продолжения решения данной задачи целесообразно задать ребятам наводящие вопросы:
Какую часть работы сделает первый плотник за год?
1 ׃ 3 = 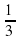 (двора)
(двора)
Какую часть работы сделает второй плотник за год?
1 ׃ 6 = 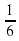 (двора)
(двора)
Какую часть работы сделают оба плотника вместе за год?
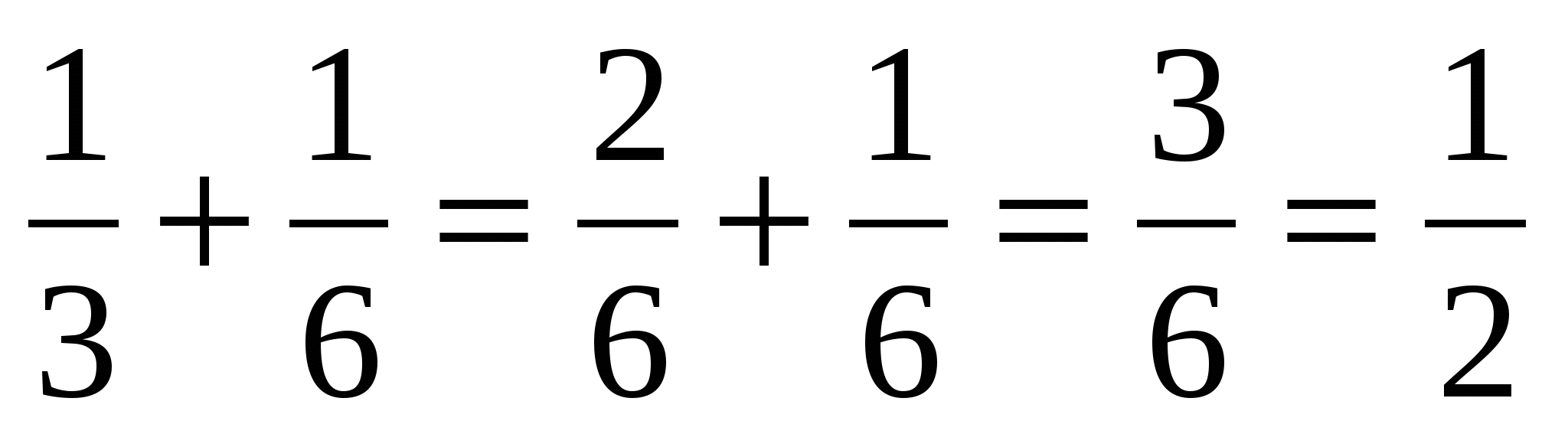 (двора)
(двора)
За сколько времени сделают они всю работу, если будут работать совместно?
1 ׃ 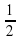 = 2 (года)
= 2 (года)
Ответ: Два плотника поставят двор, работая вместе за 2 года.
Итак. Давайте вернемся к алгоритму решения нашей задачи.
Какой вывод мы сделаем?
Запишите в своих тетрадях алгоритм решения задач на совместную работу.
Алгоритм решения задач на совместную работу:
Какую часть работы выполнит первый объект за единицу времени?
Какую часть работы выполнит второй объект за единицу времени?
Какую часть работы выполнят оба объекта вместе за единицу времени?
За сколько времени выполнят они всю работу, если будут работать совместно?
Задача 1.
В городе есть искусственный водоем. Одна из труб может заполнить его за 4 часа, вторая – за 8часов, а третья – за 24 часа. За сколько времени наполнится водоем, если открыть сразу три трубы?
Решение:
1 : 4 = 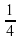 (водоема) – наполнится через первую трубу за час.
(водоема) – наполнится через первую трубу за час.
1 : 8 = 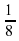 (водоема) – наполнится через вторую трубу за час.
(водоема) – наполнится через вторую трубу за час.
1 : 24 = 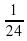 (водоема) – наполнится через третью трубу за час.
(водоема) – наполнится через третью трубу за час.
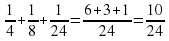 (водоема) – наполнится через три трубы за час.
(водоема) – наполнится через три трубы за час.
1: 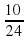 = 1·
= 1· 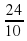 = 2,4 (ч)
= 2,4 (ч)
Ответ: через три трубы, работающие одновременно, водоем наполнится за 2,4ч.
Таким образом, при решении задач на совместную работу складывается не время работы, а часть работы, которую делают ее участники.
Итак, алгоритм.
При решении задач на совместную работу вся выполненная работа принимается за единицу.
а) Находим часть работы выполненной одним объектом за единицу времени (производительность Р1). (Р = 1/Т)
б) Находим часть работы выполненной другим объектом за единицу времени (производительность Р2).
в) Находим часть работы выполненной двумя и более объектами за единицу времени (производительность Р = Р1 + Р2).
г) Находим время, затраченное на выполнение всей работы всеми участвующими объектами (Т = 1 : Р).
6. Первичное закрепление изученного материала
Задача 1. Маша принесла своим друзьям медведям торт. Известно, что старший медведь может съесть торт за два дня, средний медведь за три дня, а младший за шесть дней. За сколько дней три медведя вместе съедят торт?
Решение:
1 : 2 = 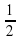 (часть торта) – съест старший медведь за 1 день
(часть торта) – съест старший медведь за 1 день
1 : 3 = 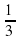 (часть торта) – съест средний медведь за 1 день
(часть торта) – съест средний медведь за 1 день
1 : 6 = 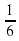 (часть торта) – съест младший медведь за 1 день
(часть торта) – съест младший медведь за 1 день
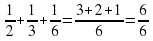 = 1 (то есть один торт) – вместе три медведя съедят торт за 1 день
= 1 (то есть один торт) – вместе три медведя съедят торт за 1 день
Ответ: за 1 день.
Кто быстрее всех решит верно, следующую задачу:
(Из «Арифметики» Л.Ф. Магницкого.) Один человек выпьет кадь пития в 14 дней, а с женою выпьет ту же кадь в 10 дней. Спрашивается, в сколько дней жена его отдельно выпьет
ту же кадь. (ответ: 35 дней)
Учитель: Давайте теперь решим задачу следующего содержания
Задача 2.
Петя и Вася красят забор за 12 часов, Вася и Коля красят этот же забор за 20 часов, Коля и Петя красят этот же забор за 15 часов, за сколько часов покрасят этот же забор Петя, Вася и Коля работая одновременно?
Решение:
1 : 12 = 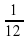 Петя и Вася за 1 час
Петя и Вася за 1 час
1 : 20 = 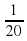 Вася и Коля за 1 час
Вася и Коля за 1 час
1 : 15 = 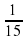 Коля и Петя за 1 час
Коля и Петя за 1 час
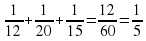 2 Пети, 2 Коли, 2 Васи за 1 час
2 Пети, 2 Коли, 2 Васи за 1 час
1: 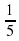 = 5 часов 2 Пети, 2 Коли, 2 Васи
= 5 часов 2 Пети, 2 Коли, 2 Васи
5 · 2 = 10 часов.
Ответ: за 10 часов.
7. Самостоятельное решение подобных задач по рядам с самопроверкой
Задача 3. Один ученик может убрать класс за 20 мин, а второй за 30 мин. За сколько минут они могут убрать класс, работая вместе?
Задача 4. Через первую трубу водоем можно наполнить за 5ч, а через вторую – за 6 ч. За сколько часов наполнится водоем при совместной работе этих труб?
Задача 5. Грузовая машина проезжает расстояние между двумя городами за 3 ч, а легковая – за 2 ч. Машины одновременно выехали из этих городов навстречу друг другу. Через сколько часов они встретятся?
8. Рефлексия деятельности
С помощью беседы обсудить с учащимися вопросы:
– Задачи, какого типа научились решать?
– Что нового на уроке узнали?
– Что научились делать?
– Что находим первоначально при решении задач на совместную работу?
– Где испытывали затруднения?
9. Домашнее задание.
Составить две задачи на совместную работу и решить их.
Используемая литература
http://www.torrentino.com/torrents/709208
http://reshuege.ru/test?theme=87
http://www.matznanie.ru/xbookM0001/index.html?go=part-047*page.htm
Система задач продвинутого уровня.
1. Первая бригада, работая отдельно, может выполнить заказ по ремонту участка дороги за 3 дня, а вместе со второй бригадой за 2 дня. За сколько дней одна вторая бригада может выполнить заказ по ремонту этого же участка дороги.
2. Четыре человека хотят двор строить. Первый из них может построить двор в 1 год, второй - в 2 года, третий - в 3 года, а четвертый в 4 года. Спрашивается, в сколько годов они вместе построят тот двор?
3. Одна мастерская должна была изготовить 420 деталей; другая за тот же срок 500 деталей. Первая выполнила свою работу на 4 дня раньше срока, а вторая на 7 дней. По скольку деталей в день изготовляла каждая мастерская, если вторая мастерская ежедневно изготовляла на 5 деталей больше?
4. Двое рабочих выполнили всю работу за 10 дней, причем последние два дня первый из них не работал. За сколько дней первый рабочий выполнил бы всю работу, если известно, что за первые семь дней они вместе выполнили 80 % всей работы. (14 д).
5. Два трактора вспахивают поле, разделенное на две равные части. Оба трактора начали одновременно, и каждый вспахивает свою половину. Через 5 часов после того момента, когда они совместно вспахивали половину всего поля, выяснилось, что первому трактору осталось вспахать 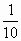 часть своего участка, а второму -
часть своего участка, а второму - 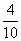 своего участка. Сколько времени понадобится второму трактору, чтобы одному вспахать все поле? (50 ч).
своего участка. Сколько времени понадобится второму трактору, чтобы одному вспахать все поле? (50 ч).
6. В бассейн проведены три трубы. Одна первая труба наполняет бассейн в 2,6 раза быстрее, чем одна вторая труба, а одна вторая труба наполняет бассейн на 3 часа медленнее, чем одна третья труба. За сколько часов одна третья труба наполняет бассейн, если все три трубы, работая одновременно, наполняют бассейн за 3 ч 45 мин. (15 ч)
7. Два насоса , работая вместе, наполняли бассейн за 8 ч. После ремонта насосов производительность первого из них увеличилась в 1,2 раза, а второго - в 1,6 раза. В результате они стали наполнять бассейн за 6 ч. За сколько часов наполнит бассейн один лишь первый насос после ремонта. (10 ч).
8. (№ 7.21 Сборник для подготовки к экзаменам в 9 классе по новой форме. Кузнецова).
Кондитер и его ученик вместе изготовили 140 пирожных, причем кондитер, работал на 1 ч меньше, чем ученик. Известно, что кондитер изготавливает в час на 6 пирожных больше, поэтому, он изготовил на 20 пирожных больше, чем ученик. Сколько пирожных в час изготавливает кондитер и сколько ученик?
9. Две копировальные машины печатают рукопись. Если всю рукопись будет печатать первая машина, то работа будет выполнена на 4 мин позже, чем две машины, работая вместе. Если печатать всю рукопись будет вторая машина, то она напечатает на 25 мин позже, чем обе машины, работая вместе. За сколько минут может напечатать эту рукопись вторая машина? (35 мин).
10. Две швеи выполняют некоторый заказ. После 45 мин совместной работы первую швею срочно вызвали к начальству, и вторая швея закончила оставшуюся часть работы за 2 ч 15 мин. За какое время могла бы выполнить всю работу каждая швея в отдельности, если известно, что второй швее для этого понадобится на 1 час больше, чем первой?
11. Некоторый объект первоначально начали строить 40 рабочих; через 6 дней к ним присоединились еще 10 рабочих, а через 6 дней после этого - еще 10 рабочих. Сколько дней продолжалась постройка объекта, если известно, что те же 60 рабочих окончили бы её в 11 дней, если бы начали работу одновременно? (14 дней).
12. Трава на лугу растет одинаково быстро и густо. Известно что 70 коров поели бы её за 24 дня, а 30 коров - за 60 дней. Сколько коров поели бы всю траву за 96 дней. (20).
13.Три каменщика выложили стену. Первый работал 6ч, второй - 4 ч, третий - 7 ч. Если бы первый работал 4 ч, второй - 2 ч, третий - 5 ч, то они выложили бы 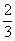 стены. За сколько часов они выложили бы стену вместе? (6 ч)
стены. За сколько часов они выложили бы стену вместе? (6 ч)
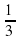 часть бассейна наполнится за 1 час.
часть бассейна наполнится за 1 час. 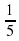 часть работы выполняли каждый час.
часть работы выполняли каждый час.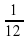 часть бассейна. За сколько часов она наполнит бассейн?
часть бассейна. За сколько часов она наполнит бассейн?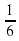 часть пути. За сколько часов он пройдет весь путь?
часть пути. За сколько часов он пройдет весь путь?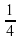 бассейна, а вторая –
бассейна, а вторая – 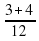 =
= 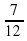 (часть бассейна) – наполняют обе трубы за 1 час
(часть бассейна) – наполняют обе трубы за 1 час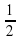
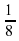 (водоема) – наполнится через вторую трубу за час.
(водоема) – наполнится через вторую трубу за час.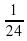 (водоема) – наполнится через третью трубу за час.
(водоема) – наполнится через третью трубу за час.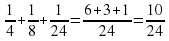 (водоема) – наполнится через три трубы за час.
(водоема) – наполнится через три трубы за час.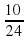 = 1·
= 1· 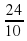 = 2,4 (ч)
= 2,4 (ч)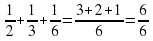 = 1 (то есть один торт) – вместе три медведя съедят торт за 1 день
= 1 (то есть один торт) – вместе три медведя съедят торт за 1 день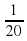 Вася и Коля за 1 час
Вася и Коля за 1 час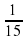 Коля и Петя за 1 час
Коля и Петя за 1 час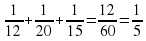 2 Пети, 2 Коли, 2 Васи за 1 час
2 Пети, 2 Коли, 2 Васи за 1 час