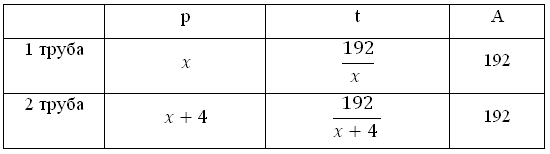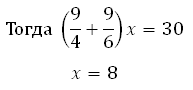Решение задач на совместную работу.
Умение решать задачи на работу может очень пригодиться в практической жизни. Следующие примеры показывают, насколько разнообразными могут быть задачи на работу.
- Начальник смены в супермаркете хочет оценить, насколько быстрее пройдет очередь, если открыть еще одну кассу, на которой будет работать стажер, обслуживающий клиентов вдвое медленнее опытного сотрудника.
- Катя и Света узнали, что у Саши - день рождения. И сразу стали набирать СМС-ки. Катя умеет набирать 24 слова за 4 минуты, а Света - 35 слов за 7 минут. Катя набрала поздравление из 30 слов, а Света - из 20. Чье поздравление Саша получит первым?
Чтобы получить приличную оценку на ЕГЭ, обучающихся необходимо научить решать подобные задачи. Сделать это не сложно, поскольку большинство из них решается по стандартному алгоритму.
Как и во всех текстовых задачах, начинать решение следует с внимательного чтения условия и выбора переменной. После того как переменная выбрана, следует перевести условие на математический язык, то есть составить уравнение или систему уравнений. Если вы все сделали правильно, то должно получиться линейное или квадратное уравнение, и все, что остается сделать, — не ошибиться в арифметике.
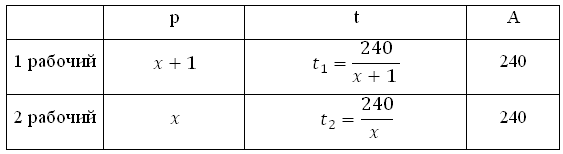
Составить уравнения в задаче на работу очень просто. Нам понадобится всего лишь одна формула: A=p·t.
Здесь A — это объем работы, t — это время выполнения работы, а p — это величина, которая по смыслу означает скорость выполнения работы и называется "производительность труда".
Чем так хороша производительность труда? А тем, что производительности труда нескольких человек можно складывать. Это значит, что, для того чтобы получить производительность труда группы из нескольких человек, нужно сложить производительность труда людей в группе. Поэтому, при составлении уравнения в качестве переменной x удобно выбрать производительность.
Если объем работы не указан, то его следует принять за единицу.
Общий план решения:
1. Выбрать переменную (обычно производительность)
2. Заполнить табличку (A,t,p) для каждого из рабочих (или для каждой из труб в задачах про трубы), используя формулу A=t·p
3. Переписать условие в виде уравнения
4. Привести полученное уравнение к виду квадратного или линейного уравнения
5. Решить уравнение и отобрать подходящий по смыслу корень (если их два)
6. Найти ответ в задаче (если нужно найти не производительность, а другую величину)
Решая задачи на совместную работу по заданному алгоритму легко подготовить обучающихся к сдаче экзаменов и вселить в них уверенность, что они со всем справятся!