Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Факультативное занятие по теме "Решение текстовых задач на совместную работу"
Одним из важных вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач. Учебные математические задачи являются очень эф¬фективным и часто незаменимым средством усвоения учащимися понятий и методов школьного курса математики, вообще математиче¬ских теорий. Велика роль задач в развитии мышления и в математиче¬ском воспитании учащихся, в формировании у них умений и навыков в практических применениях математики. Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Текстовые задачи входят в ГИА и ЕГЭ, являются традиционным разделом на вступительных экзаменах в Вузы. Таким образом, данная тема имеет важнейшее значение в обучении математике.
Цель предлагаемого материала:
• научить находить способ решения задач с помощью использования опорных задач
на совместную работу;
• научить использовать арифметический способ решения текстовых задач,
• развивать смекалку и сообразительность, умение ставить вопросы и отвечать на них.
Задачи на совместную работу.
В задачах на совместную работу обычно какую либо работу выполняют несколько человек или механизмов, работающих с постоянной для каждого из них производительностью.
Основными компонентами задач являются:
• Объём выполняемой работы - А
(если он неизвестен и не является искомым, то принимается за 1),
• Время - t,
• Производительность - p.
Задачи на работу делятся на два типа:
• задачи, в которых выполняется раздельная работа - эти задачи решаются аналогично задачам на движение.
Например: Первая труба пропускает на 3 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 648 литров она заполняет на 3 минуты быстрее, чем первая труба?
Данную задачу можно решить с помощью уравнения. Для этого удобно воспользоваться последовательно заполняемой таблицей:
Пропускная способность Время Объем резервуара
Первая труба х - 3
648
Вторая труба х
648
По условию задачи вторая труба заполняет резервуар на 3 мин. быстрее, чем первая труба, следовательно величина на 3 меньше, чем величина . Составим уравнение:
+ 3 = ; + 3 - = 0; разделим обе части уравнения на 3
; выполним действия в левой части уравнения и упростим числитель дроби
решив данную систему, получим х = 27 и х = - 24
Ответ: 27 литров в минуту
• задачи на совместную работу.
Если в задаче встречаются слова "выполнили работу вместе" или слова "совместная работа", значит это задача на совместную работу.
В задачах на совместную работу мы имеем дело с теми же тремя параметрами, что и в задачах на раздельную работу:
• Объем работы (А)
• Время (t)
• Производительность (p).
Данные величины связаны между собой формулой:
Рассмотрим некоторые виды задач на совместную работу.
1) Вычисление неизвестного времени работы.
Бригада слесарей может выполнить некоторое задание по обработке деталей на 1,5 ч скорее, чем бригада учеников. Если бригада учеников отработает 18 ч, выполняя это задание, а потом бригада слесарей продолжит выполнение задания в течение 6 ч, то и тогда будет выполнено только 3/5 всего задания. Сколько времени требуется бригаде учеников для самостоятельного выполнения данного задания?
Решение:
Пусть вся работа может быть выполнена бригадой учеников за х часов, бригадой слесарей – за (х – 15) часов.
Всю работу примем за 1.
Тогда производительность бригады учеников , а производительность бригады слесарей.
- часть работы, выполненная бригадой учеников;
- часть работы, выполненная бригадой слесарей.
Составим уравнение и решим его:
Корни уравнения: 45 и 10 ( 10 – посторонний корень, так как бригада учеников выполняла задание на 15 часов дольше, чем бригада слесарей)
Ответ: 45 часов
2) Задачи на «бассейн», который наполняется разными трубами.
Для наполнения контейнера водой имеются три трубы. Первой трубе для наполнения контейнера необходимо времени в три раза меньше, чем второй, и на 2 ч больше, чем третьей. Три трубы, работая одновременно, наполнили бы контейнер за 3ч, но по условиям эксплуатации одновременно могут работать только две трубы. Определите минимальную стоимость наполнения контейнера, если стоимость 1ч работы одной из труб равно 230 рублей.
Решение: Задачу удобно решать с помощью таблицы.
Примем всю работу за 1.
Время Производительность Работа
1 труба
(2 + х) ч
3часа
1
2 труба
3(2 + х) ч
1
3 труба
х ч
1
Работая вместе 3 часа, производительность труб была равна 1/3. Зная, что совместная производительность равна 1/3, составим и решим уравнение:
Решая данное уравнение, получим два корня: 6 и -1. Второй корень не удовлетворяет условию задачи, следовательно, 6 часов – время, которое понадобится третьей трубе для наполнения контейнера. Значит время, которое понадобится первой трубе равно 8 часам, а второй - 24 часа.
Из полученных данных делаем вывод, что минимальное время – это время работы 1 и 3 труб, т.е. 14 часов.
Определим минимальную стоимость наполнения контейнера двумя трубами.
Ответ: 3220 рублей.
Два крана наполняют чан водой. Один кран заполняет чан на 22 мин дольше другого. Если они работают вместе, то чан наполнится водой за 1 час. Сколько времени потребуется работать каждому крану, чтобы наполнить чан?
Решение:
Пусть кран А наполняет чан за х минут, а кран В наполняет чан за у минут,
Тогда производительность каждого крана будет соответственно. Примем объем чана за 1. По условию первый кран наполняет чан на 22 мин дольше, следовательно
х – у = 22.
Так как два крана при одновременной работе наполняют чан за 1 час = 60 мин, то
или
Составим систему и решим ее:
Ответ: 132 мин; 110 мин.
3) В задачах данного типа сравнивается работа, которая должна быть выполнена по плану, и работа, которая выполняется фактически.
Так же, как и в задачах на совместную работу, основными компонентами являются: а) работа (выполненная фактически и запланированная); б) время выполнения работы(фактическое и запланированное); в) производительность труда (фактическая и запланированная).
В некоторых задачах вместо времени выполнения работы дается количество участвующих в ее выполнении рабочих.
Ученик токаря вытачивает шахматные пешки для определенного числа комплектов шахмат. Он хочет научиться изготавливать ежедневно на 2 пешки больше, чем теперь, тогда такое же задание он выполнит на 10 дней быстрее. Если бы ему удалось научиться изготавливать ежедневно на 4 пешки больше, чем теперь, то срок выполнения такого же задания уменьшился бы на 16 дней. Сколько комплектов шахмат обеспечивает пешками этот токарь, если для каждого комплекта нужно 16 пешек?
Решение:
Пусть токарь вытачивает х пешек для определенного числа комплектов шахмат, при этом в день он вытачивает у пешек.
Тогда задание он выполнит за дней.
Если он будет вытачивать в день (у + 2) пешки или (у + 4) пешки, то он выполнит задание за дня.
На основании условия задачи составим систему уравнений и решим ее:
Так как на каждый комплект нужно 16 пешек, то число комплектов равно 240 : 16 = 15.
Ответ: 15 комплектов.
Бригада рыбаков намеревалась выловить в определенный срок 1800 ц рыбы. Треть этого срока был шторм, вследствие чего плановое задание ежедневно недовыполнялось на 20 ц. Однако, в остальные дни бригаде удавалось ежедневно вылавливать на 20 ц больше дневной нормы, и плановое задание было выполнено за день до срока. Сколько центнеров рыбы намеревалась вылавливать бригада рыбаков ежедневно?
Решение: данные задачи удобно внести в таблицу
Время Улов за 1 день Весь улов
По плану
х дней у ц 1800 ц
Фактически в шторм
дней
(у – 20) ц
1800 ц
после шторма
дней
(у + 20) ц
Составим и решим систему:
Ответ: 100 ц.
Планом было предусмотрено, что предприятие на протяжении нескольких месяцев изготовит 6000 насосов. Увеличив производительность труда, предприятие стало изготовлять в месяц на 70 насосов больше, чем было предусмотрено, и на один месяц раньше установленного срока перевыполнило задание на 30 насосов. На протяжении скольких месяцев было предусмотрено выпустить 6000 насосов?
Решение:
Пусть за х месяцев планировали выполнить задание, тогда за (х – 1) месяц было выпущено 6030 насосов.
По плану предприятие планировало выпускать насосов, а фактически выпустило в месяц насосов. Составим и решим уравнение:. Решая это уравнение получим: х1 = 10; х2 = (х2 не удовлетворяет условию задачи).
Ответ: 10 месяцев
Бригада каменщиков взялась уложить 432 м3 кладки, но в действительности на работу вышло на 4 человека меньше. Сколько всего каменщиков в бригаде, если известно, что каждому работавшему каменщику пришлось укладывать на 9 м3 больше, чем первоначально предполагалось?
Решение:
Пусть в бригаде х каменщиков. Тогда по условию задачи на работу вышло (х – 4) каменщиков.
Каждый каменщик должен был по плану уложить м3, фактически же каждый уложил м3. Из условия следует уравнение, решая которое, находим х = 16.
Ответ: 16 человек.
Задачи для самостоятельной работы
1. Заказ на 130 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 3 детали больше?
Ответ: 13 дет.
2. Двое рабочих, работая вместе, могут выполнить работу за 9 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 5 дней выполняет такую же часть работы, какую второй — за 3 дня?
Ответ: 24 дня
3. Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 165 литров она заполняет на 4 минуты дольше, чем вторая труба?
Ответ: 11 литров
4. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 156 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 143 литра?
Ответ: 12 литров
5. Два рабочих, из которых второй начал работать полутора днями позже первого, работая независимо один от другого, оклеили обоями несколько комнат за 7 дней, считая с момента выхода на работу первого рабочего. Если бы эта работа была поручена каждому отдельно, то первому для ее выполнения понадобилось бы тремя днями больше, чем второму. За сколько дней каждый из них отдельно выполнил бы эту же работу?
Ответ: 14 и 11 дней.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Факультативное занятие по теме "Решение текстовых задач на совместную работу"»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1510 руб.
2510 руб.
1690 руб.
2820 руб.
1690 руб.
2820 руб.
1800 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
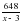
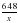
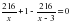 ; выполним действия в левой части уравнения и упростим числитель дроби
; выполним действия в левой части уравнения и упростим числитель дроби
 решив данную систему , получим х = 27 и х = - 24
решив данную систему , получим х = 27 и х = - 24 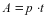
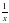 , а производительность бригады слесарей
, а производительность бригады слесарей 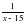 .
. - часть работы, выполненная бригадой учеников;
- часть работы, выполненная бригадой учеников;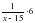 - часть работы, выполненная бригадой слесарей.
- часть работы, выполненная бригадой слесарей.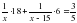
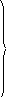
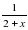
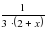
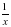
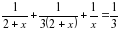
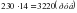
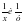 . Примем объем чана за 1. По условию первый кран наполняет чан на 22 мин дольше, следовательно
. Примем объем чана за 1. По условию первый кран наполняет чан на 22 мин дольше, следовательно 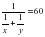 или
или 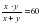
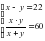
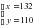 Ответ: 132 мин; 110 мин.
Ответ: 132 мин; 110 мин.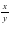 дней.
дней. дня.
дня.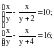
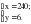
 дней
дней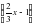 дней
дней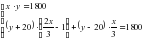
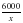 насосов, а фактически выпустило в месяц
насосов, а фактически выпустило в месяц 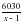 насосов. Составим и решим уравнение:
насосов. Составим и решим уравнение: 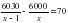 . Решая это уравнение получим: х1 = 10; х2 =
. Решая это уравнение получим: х1 = 10; х2 = 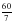 (х2 не удовлетворяет условию задачи).
(х2 не удовлетворяет условию задачи). м3, фактически же каждый уложил
м3, фактически же каждый уложил 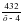 м3. Из условия следует уравнение
м3. Из условия следует уравнение  , решая которое, находим х = 16.
, решая которое, находим х = 16.















