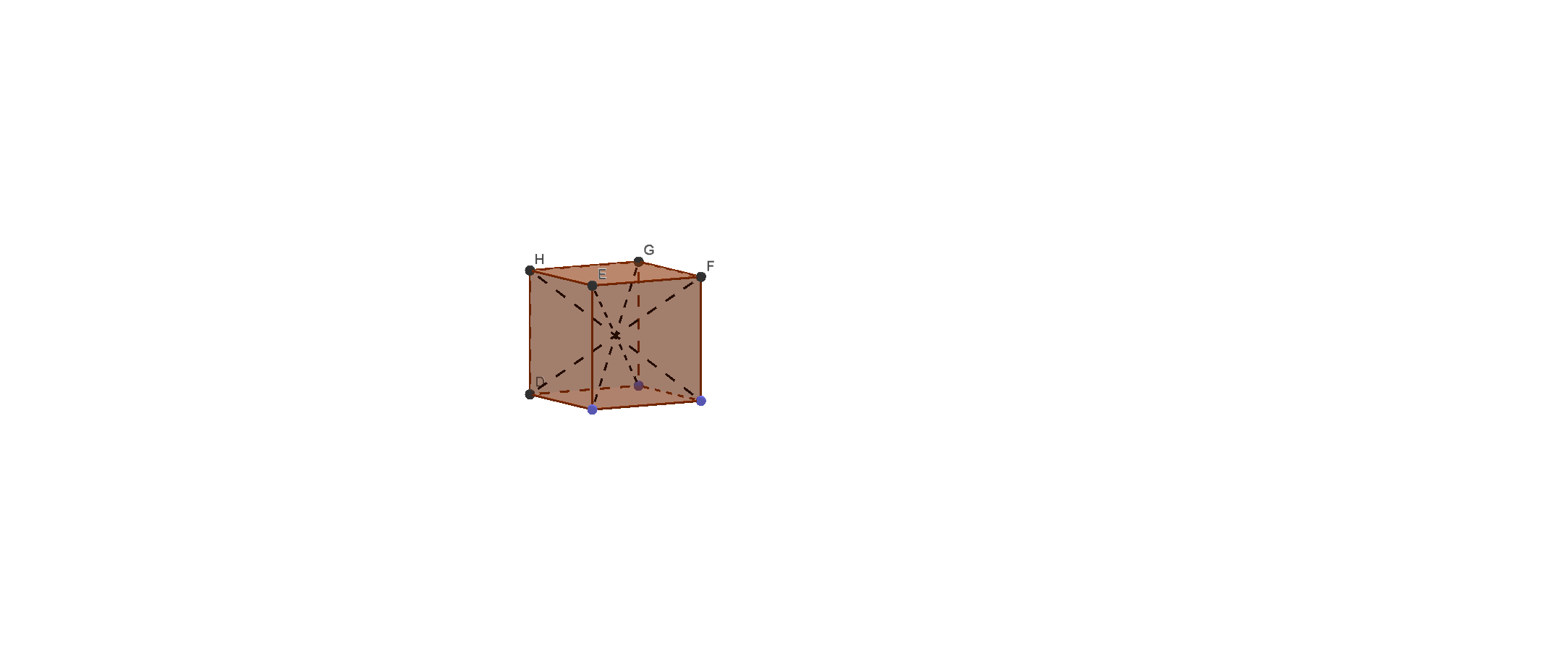
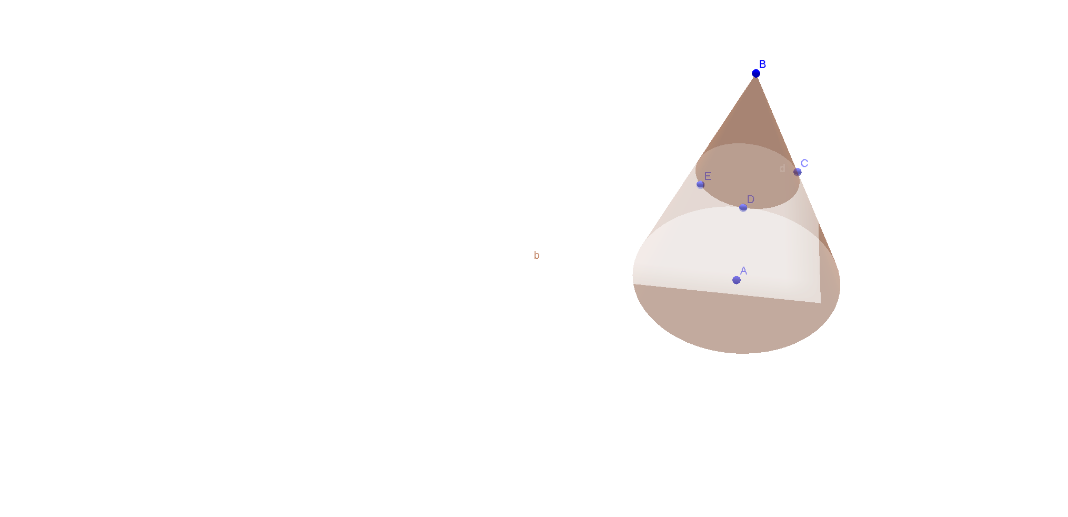
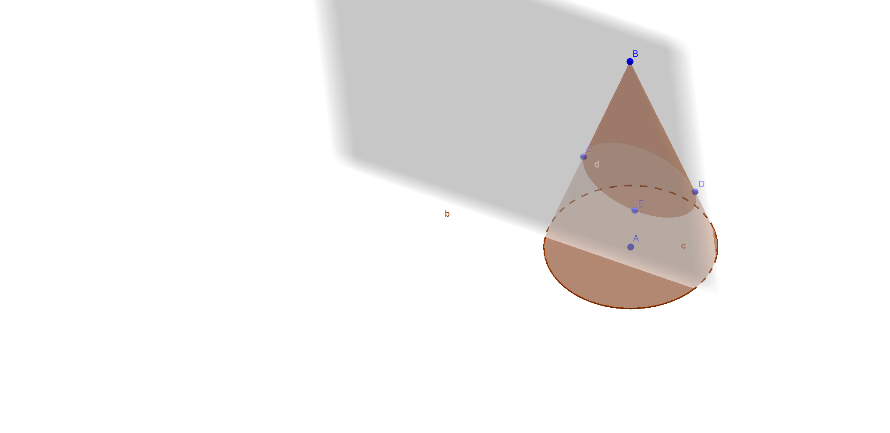
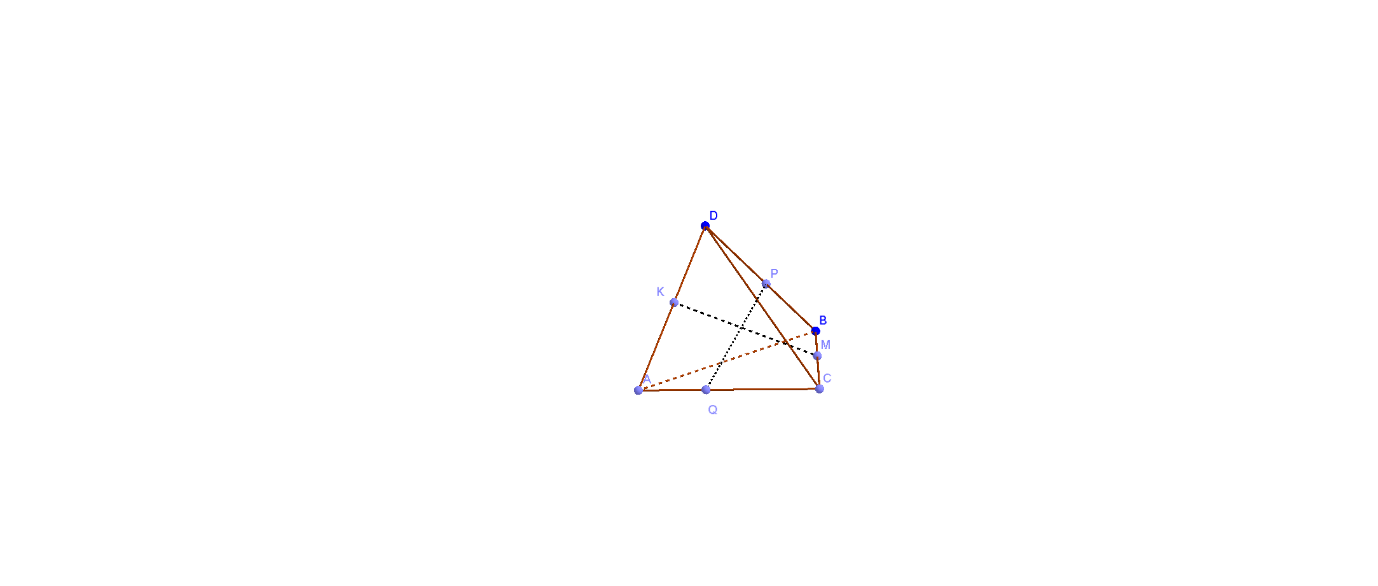
В современной системе образования основная задача, которая ставится перед учителем, целенаправленно развивать интеллектуальную активность и самостоятельность у обучающихся. Основная роль в связи с этим возложена на предметы математического цикла. С одной стороны, наиболее большим развивающим потенциалом обладает геометрия, с другой стороны, учащиеся больше предпочитают заниматься алгеброй. Практика показывает, что особенно сильно этот перекос в сторону алгебры наблюдается в 10 классе, когда для решения стереометрических задач необходимо развитое пространственное воображение и представление, которое обычно не сформировано в должной степени на предыдущих этапах обучения. Общепринятый подход к раздельному изучению планиметрии и стереометрию на мой взгляд неприемлем и поэтому на протяжении многих лет в своей практической деятельности использую учебно - методический комплект авторского коллектива Шарыгина И. Ф. Предпочтение в пользу этого УМК определяется особенностью данного курса, где трехмерное пространство выступает своеобразным интерьером для плоской геометрии.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Развитие пространственного воображения на уроках математики в 5-6 классах
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Развитие пространственного воображения на уроках математики в 5-6 классах »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
2220 руб.
3170 руб.
1970 руб.
2820 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



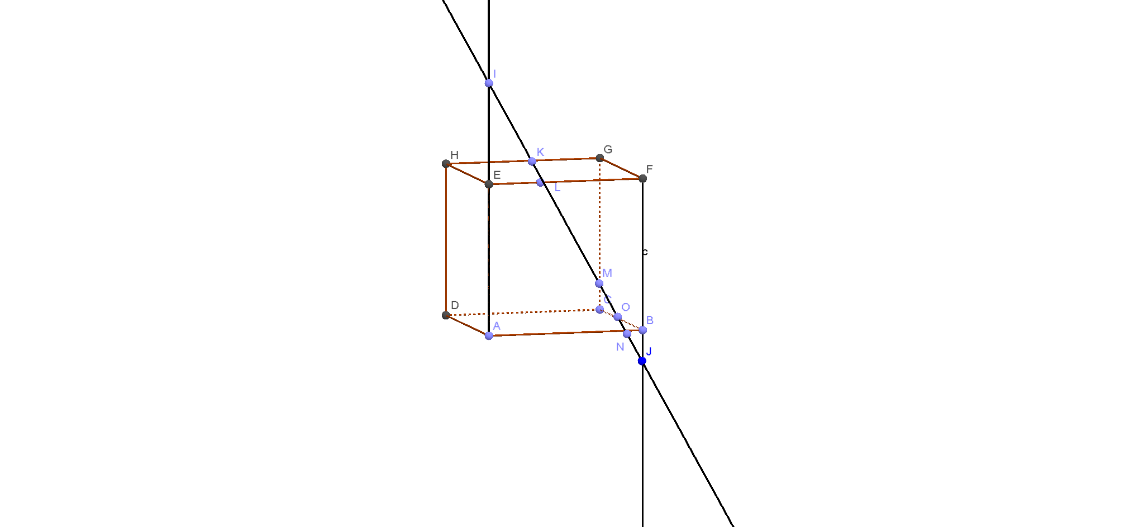
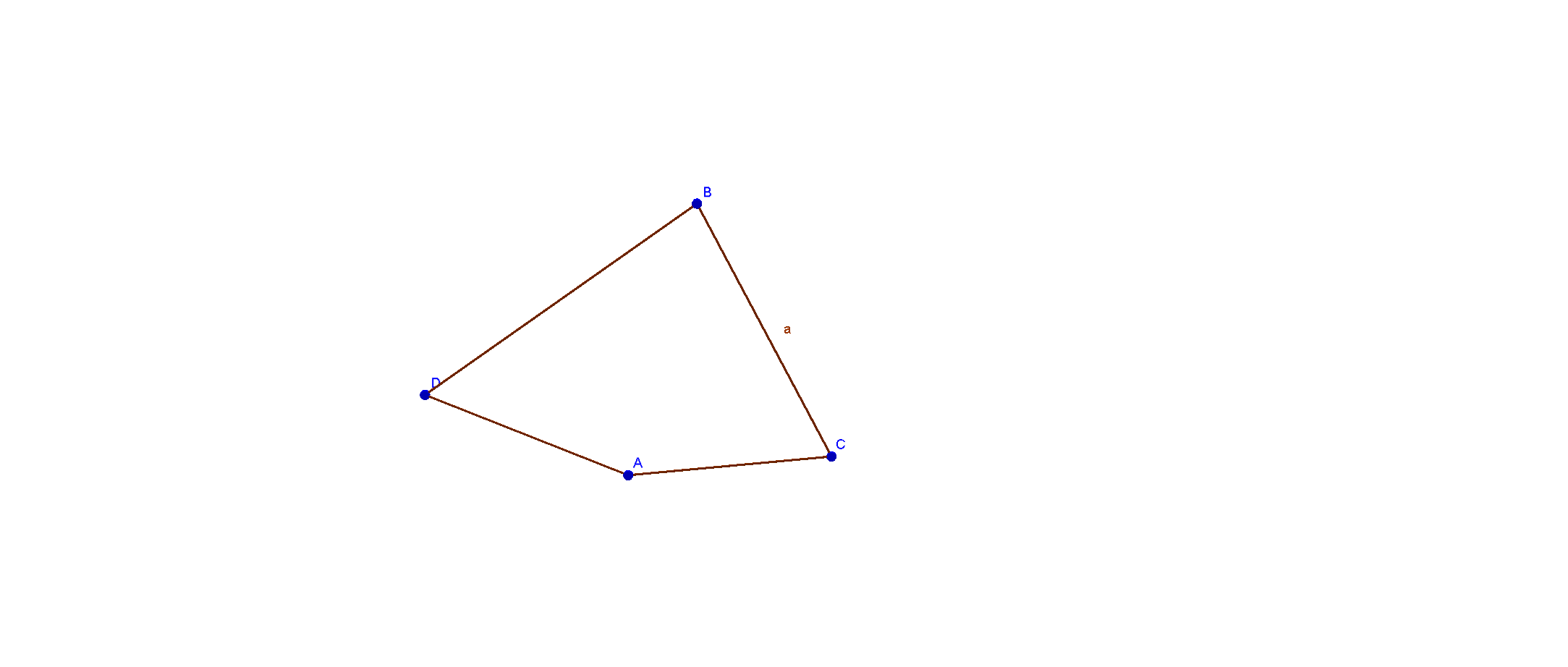
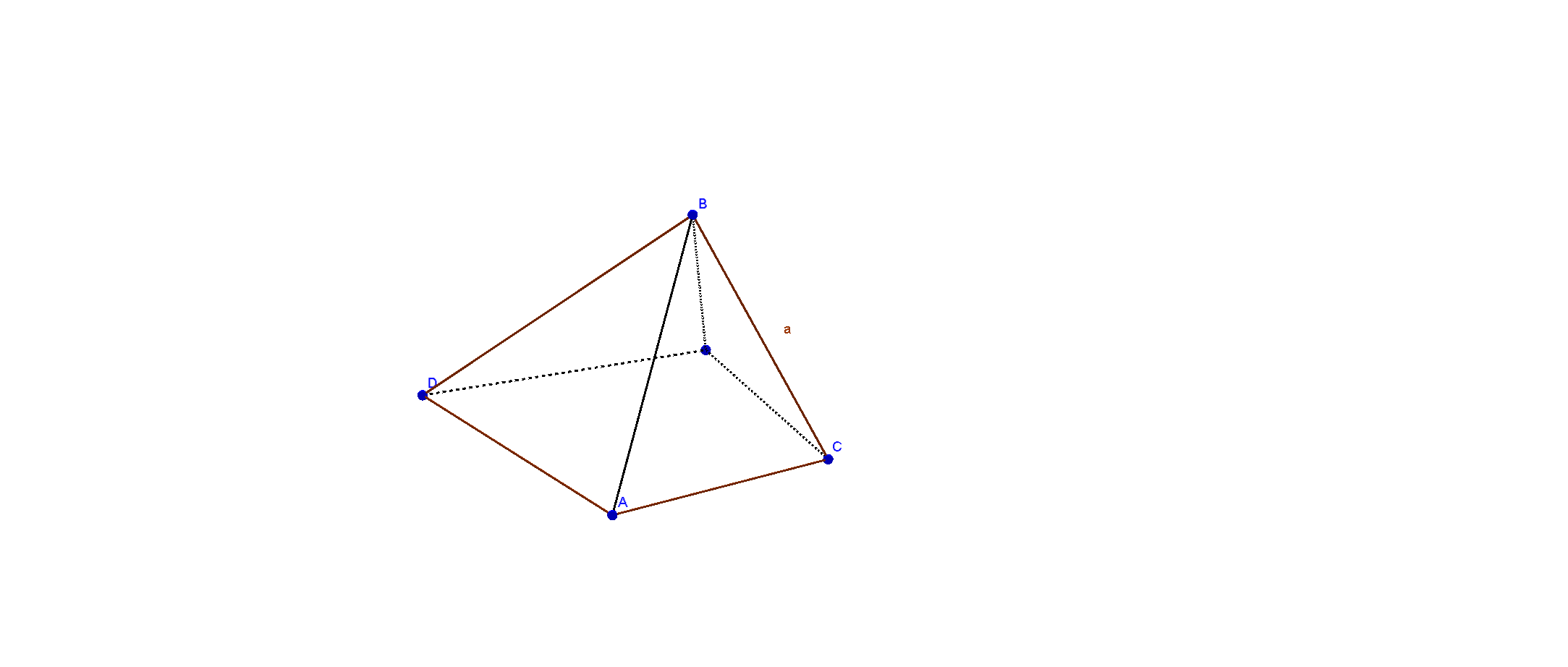
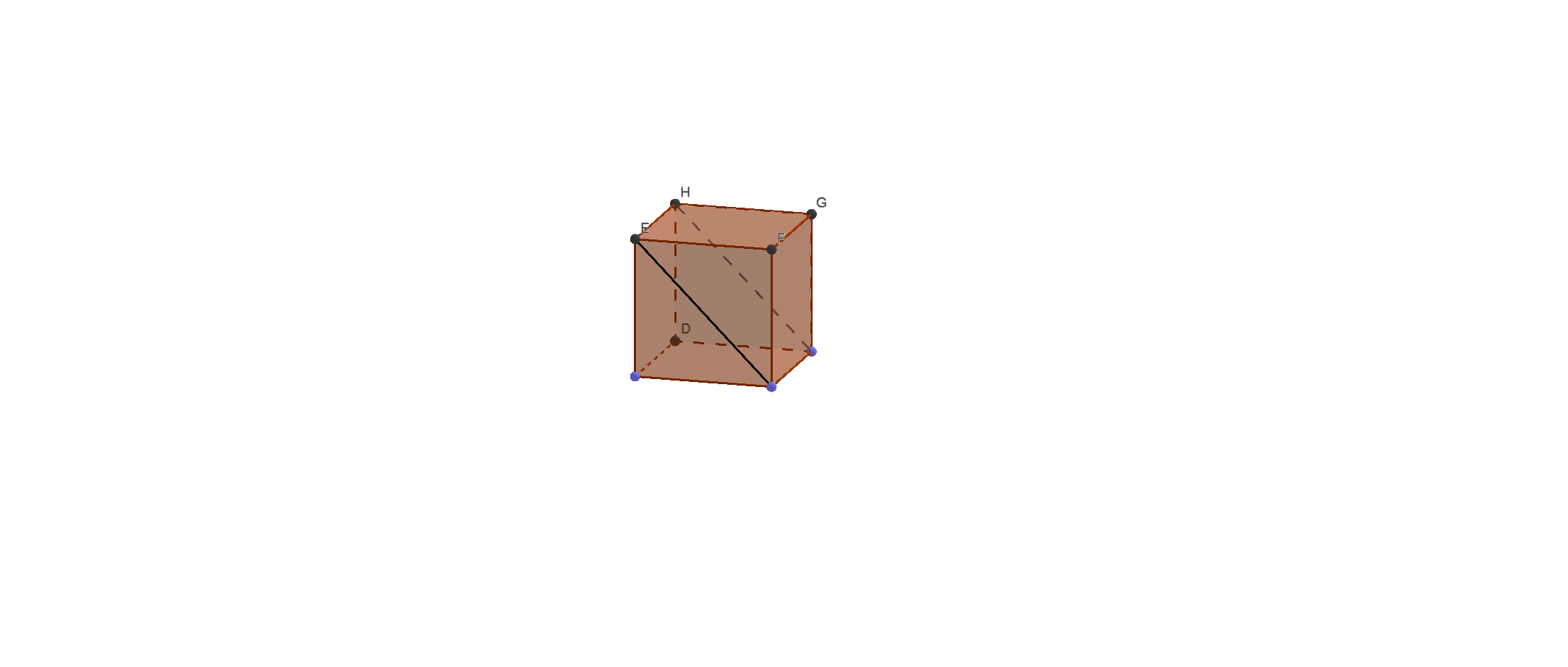 Рис.3
Рис.3