Работа содержит сведения из истории комбинаторики, решение основных видов задач по комбинаторике.
- Меню
- Главная
- Дошкольное образование
- Начальные классы
- Астрономия
- Биология
- География
- Информатика
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- Русский язык
- Английский язык
- Немецкий язык
- Французский язык
- История
- Естествознание
- Всемирная история
- Всеобщая история
- История России
- Право
- Окружающий мир
- Обществознание
- Экология
- Искусство
- Литература
- Музыка
- Технология (мальчики)
- Технология (девочки)
- Труд (технология)
- Физкультура
- ИЗО
- МХК
- ОБЗР (ОБЖ)
- Внеурочная работа
- ОРК
- Директору
- Завучу
- Классному руководителю
- Экономика
- Финансовая грамотность
- Психологу
- ОРКиСЭ
- Школьному библиотекарю
- Логопедия
- Коррекционная школа
- Всем учителям
- Прочее
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
- Главная
- Математика
- Прочее
- Проектная работа "Комбинаторные задачи"
Проектная работа "Комбинаторные задачи"
Просмотр содержимого документа
«Проектная работа "Комбинаторные задачи"»
СОДЕРЖАНИЕ
«ОСОБАЯ ПРИМЕТА» КОМБИНАТОРНЫХ ЗАДАЧ……………..…………………………3
СВЕДЕНИЯ ИЗ ИСТОРИИ……………………………………………………............................4
Комбинаторика в Древнем Китае………………….…………………...............................4
Комбинаторика в Древней Греции………………….…………………............................5
Мистики, астрологи, каббалисты………………….…………………..............................7
Комбинаторика в странах Востока…………………..………………………………….8
Liber Abaci………………………………………..……………………………………….10
Игра в кости…………………………………………………………………………….....11
Игрок и ученые………………………….……….…………………………………….....12
Новая ветвь математики……………………………………………………………….....13
Комбинаторика и шифры………………………….…………………………………....14
Анаграммы ………………………….…………..................................................................15
Иероглифы и клинопись …………………….………………...........................................17
ПЕРЕСТАНОВКИ……………………………………………………………………………...21
Решение задачи о квартете……………………………….……………………………...22
Зеркально-симметричные перестановки………….……………………………………...22
Перестановки с повторениями ………………………….…….……….………….……...23
РАЗМЕЩЕНИЯ………………………………………….……………………………………...25
Есть ли у нуля факториал? ………………………….……………………………………...25
Размещения с повторениями ………………………..……………………………………...26
Решение задачи о паспортах …………………………………………………..…………...27
СОЧЕТАНИЯ…………………………………………………………………………………...28
Задача о Лотто-Миллион …………………………………………………………….……29
Сочетания с повторениями ………………………………………………………………30
БИНОМ НЬЮТОНА …………….………………………………………………………………..32
Биномиальные коэффициенты и сочетания ………………………………………………...33
Свойства биномиальных коэффициентов…………………………………………………...34
Треугольник Паскаля……………………………………………………………………….……34
ЗАДАЧИ ПО КОМБИНАТОРИКЕ……………………………………………………………36
Задача о разбиении плоскости прямыми……………………………………………………...36
Задача о разбиении пространства плоскостями………………………………..………..37
Обобщённый факториал и числа Каталана………………………….………………….38
ЗАКЛЮЧЕНИЕ………………………………………………………………………………..40
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ…………………………………...……...41
«ОСОБАЯ ПРИМЕТА» КОМБИНАТОРНЫХ ЗАДАЧ
В знаменитой басне Крылова «Квартет» «проказница Мартышка, Осёл, Козёл да косолапый Мишка» устроили любопытный эксперимент: они исследовали влияние взаимного расположения музыкантов на качество исполнения. И если бы не вмешался Соловей, участники квартета, наверное, перепробовали бы все возможные варианты. Зададимся вопросом: сколько существует способов, чтобы рассадить, например в один ряд, четырёх музыкантов?
Другой случай. Воспетый Маяковским «молоткастый, серпастый» советский паспорт имел серию и номер, состоящие в общей сложности из трёх частей:
1) некоторое число, записанное римскими цифрами;
2) две русские буквы;
3) шесть арабских цифр.
Например, IХ-РГ № 062993. Разумеется, все паспорта должны иметь разные номера. Сколько может быть различных паспортов?
Третья ситуация. Нас приглашают сыграть в Лотто-Миллион. Суть игры в том, что нужно из 49 номеров угадать б, которые выпадут во время тиража. Для участия в игре следует приобрести специальную карточку и вычеркнуть в ней 6 любых квадратов, пронумерованных числами от 1 до 49. Чтобы выиграть наверняка, можно было бы запастись таким количеством карточек, какое необходимо для вычёркивания 6 номеров всеми возможными способами. Сколько этих способов?Общее у всех трёх задач то, что их решением занимается отдельная область математики, называемая комбинаторикой. «Особая примета» комбинаторных задач — вопрос, который всегда можно сформулировать так, чтобы он начинался словами: «Сколькими способами...».
Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.
СВЕДЕНИЯ ИЗ ИСТОРИИ
Комбинаторика в Древнем Китае
Первое упоминание о вопросах, близких к комбинаторным, встречается в китайских рукописях, относящихся к XII — XIII векам до н. э. Точно датировать эти рукописи невозможно, поскольку в 213 г. до н. э. император Ши Хуан-ди приказал сжечь все книги (они писались на бамбуковых дощечках), так что до нас дошли лишь основанные на них более поздние книги. В этих книгах писалось, что все в мире является сочетанием двух начал — мужского и женского, которое авторы обозначали символами «—» и «- -». В рукописи, сейчас известной как «Книга перемен», показаны различные соединения этих знаков по два и по три:
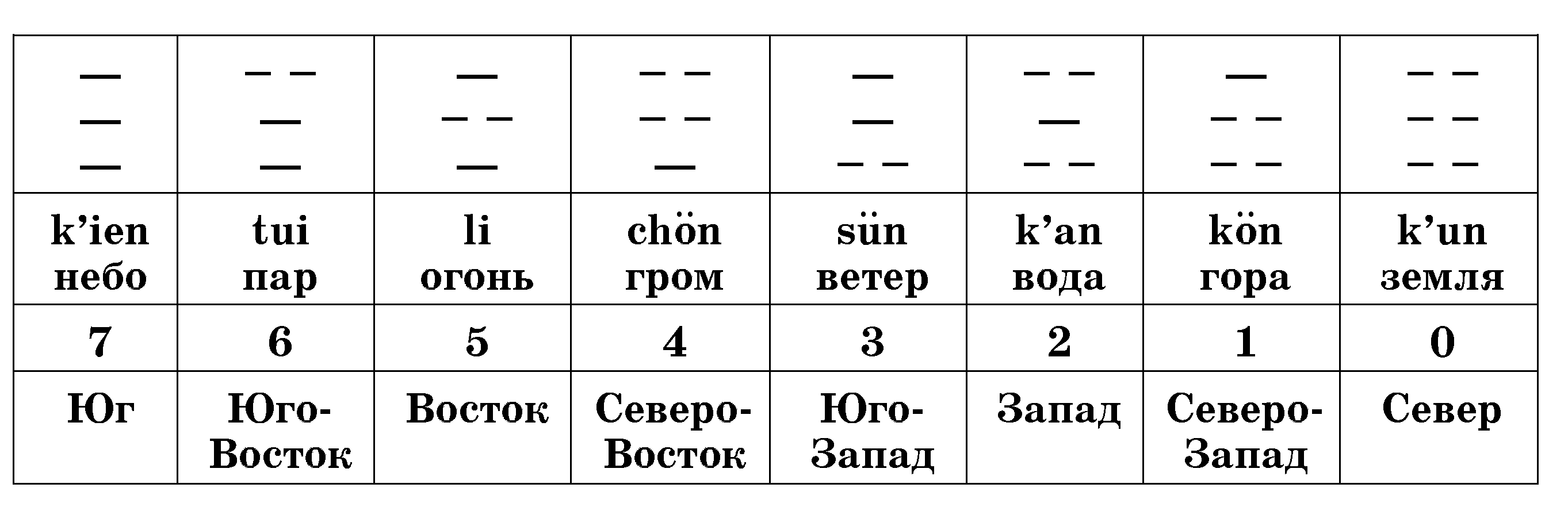
Восемь рисунков из трех рядов символов изображали землю, гору, воду, ветер, гром, огонь, пар и небо (некоторые рисунки имели и иные значения). Неудивительно поэтому, что сумма первых 8 натуральных чисел (т. е. число 36) воплощала в представлениях древних китайцев весь мир. По мере углубления знаний понадобилось выразить и другие элементы мироздания с помощью тех же знаков «—» и «- -». Были составлены 64 фигуры, содержавшие уже пять рядов черточек. Надо полагать, что удвоение числа рисунков при добавлении одного ряда символов было замечено. Это можно рассматривать как первый общий результат комбинаторики. В этой книге есть и более сложные рисунки. Как утверждает приводимое в ней предание, император Ию (по другой версии Фуси — родоначальник китайской цивилизации) более 2300 лет тому назад увидел на берегу реки Лошуй на панцире священной черепахи рисунок из белых и черных кружков (рис. 90). Если заменить каждую фигуру соответствующим числом, возникнет таблица, изображенная на том же рисунке справа. При сложении чисел в каждой строке, столбце и диагонали получается одна и та же сумма 15. При том мистическом толковании, которое придавали числам древние китайцы, открытие таблицы со столь чудесными свойствами произвело неизгладимое впечатление.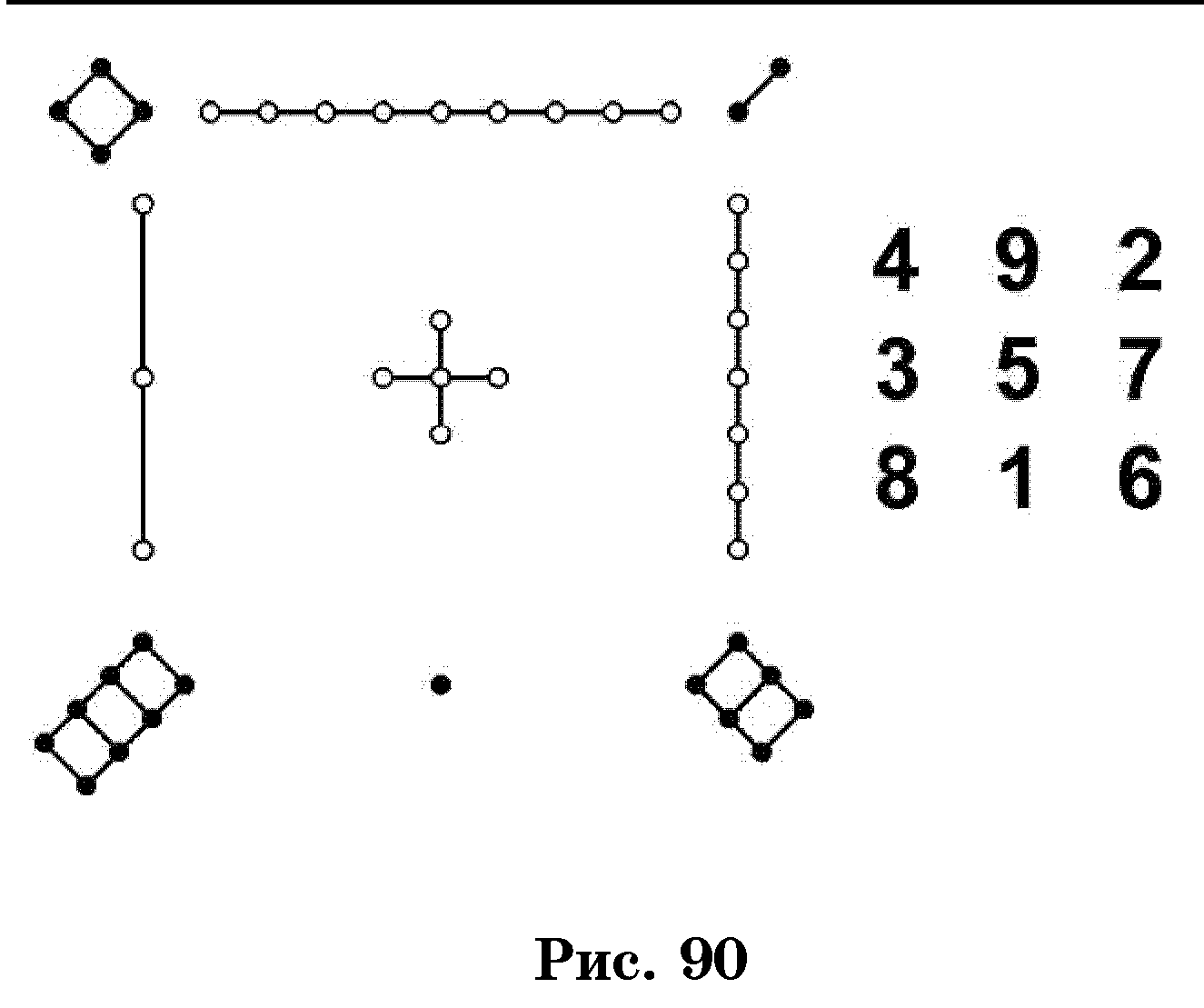
Рис. 90 назвали «ло-шу», стали считать его магическим символом и употреблять при заклинаниях. Поэтому сейчас любую квадратную таблицу чисел с одинаковыми суммами по каждой строке, столбце и диагонали называют магическим квадратом.
Комбинаторика в Древней Греции
Философ Ксенократ, живший в IV веке до н. э., подсчитывал число слогов. В III веке до н. э. стоик Хрисипп полагал, что число утверждений, получаемых из 10 аксиом, превышает миллион. По мнению же Гиппарха, из утверждающих аксиом можно составить 103049 сочетаний, а добавив к ним отрицающие, 310 952.
Мы не знаем, какой именно смысл придавали эти философы своим утверждениям и как они получали свои результаты — приводимые Гиппархом числа слишком многозначны, поэтому их нельзя считать результатом грубой оценки, и в то же время они не поддаются разумному истолкованию. По-видимому, у греческих ученых были какие-то не дошедшие до нас правила комбинаторных расчетов, скорее всего ложные.
Конкретные комбинаторные задачи, касавшиеся перечисления небольших групп предметов, греки решали без ошибок. Аристотель описал без пропусков все виды правильных трехчленных силлогизмов, а его ученик Аристоксен из Тарента перечислил различные комбинации длинных и коротких слогов в стихотворных размерах. Живший в IV веке н. э. математик Папп рассматривал число пар и троек, которые можно получить из трех элементов, допуская их повторения.
Большое внимание греческие ученые уделяли вопросам, пограничным между комбинаторикой и теорией чисел. Еще в VI веке до н. э. в школе философа и математика Пифагора возникло убеждение, что миром правят числа, а вещи только отражение чисел (возможно, что эти идеи возникли у Пифагора под влиянием вавилонской культуры и восходят к еще более древним взглядам шумеров). Поэтому, чтобы познать мир, пифагорейцы начали изучать свойства натуральных чисел. Их исследования о четных и нечетных числах, делимости чисел, простых и составных числах заложили основу теории чисел (в науке бывает, что неверные исходные установки дают толчок к полезным исследованиям).
Как и китайцы, пифагорейцы придавали особое значение числу 36 — оно было для них не только суммой первых 4 четных и первых 4 нечетных чисел, но и суммой первых трех кубов: 36 = 1 3+ 23 + 33 . Символом совершенства пифагорейцы считали совершенные числа, равные сумме своих делителей, например,
6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14, а символом дружбы — дружественные числа, каждое из которых равно сумме делителей другого числа (например, 220 и 284). Отыскание таких чисел требовало комбинаторного искусства. ь_
В школе Пифагора была доказана теорема о сторонах прямоугольного треугольника. Это вызвало интерес к представлению чисел в виде суммы двух квадратов, к квадратным числам 1, 4, 9, 16 и т. д. Квадраты натуральных чисел те изображались при этом геометрически (рис. 2). Но пифагорейцы рассматривали и иные конфигурации точек. Каждый треугольник на рис. 2 получается из предыдущего увеличением го длины его стороны на 1. Подсчитывая число точек в каждом треугольнике, получаем последовательность треугольных чисел 1, 3, 6, 10, ... Ее можно получить, последовательно складывая натуральные числа: 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4ит. д.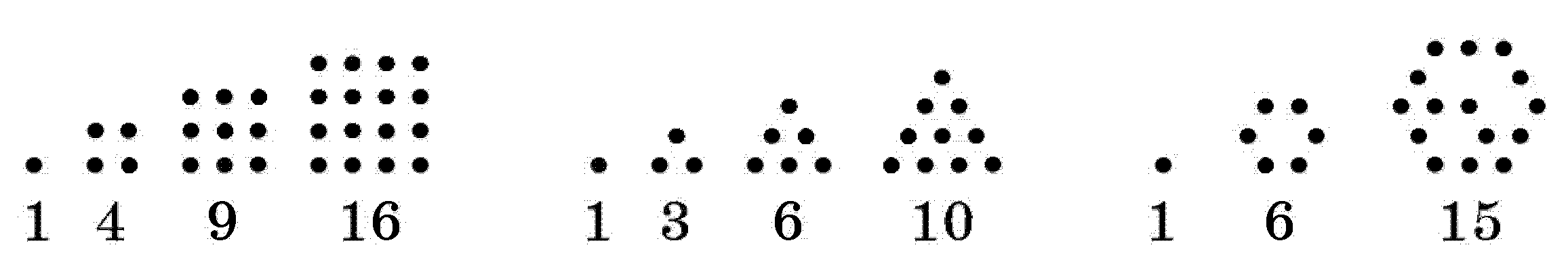
Рис.2
А шестиугольники приводят к последовательности шестиугольных чисел 1, 6, 15, ... получаемых как частичные суммы членов арифметической прогрессии 1, 5, 9 ...
В дальнейшем такие суммы удалось выразить с помощью биномиальных коэффициентов Ckn , играющих важную роль в комбинаторике.
Переход от плоскости к пространству дал возможность строить еще более сложные числа. Например, из треугольников можно составить пирамиды. Подсчитывая число точек в таких пирамидах, пришли к пирамидальным числам 1, 4, 10, 20, ..., которые были суммами ряда 1 + 3 + 6 + 10 + ..., составленного из треугольных чисел. Однако дальнейшие обобщения требовали уже введения многомерных пространств, что лежало за рамками возможностей древнегреческой математики.
Учение о фигурных числах привлекало к себе математиков на протяжении многих столетий. Ими много занимался живший в XVII веке французский ученый Пьер Ферма, который доказал, например, что любое натуральное число есть треугольное или сумма 2 или 3 треугольных чисел; квадратное или сумма 2, 3 или 4 квадратов; пятиугольное или сумма 2, 3, 4 или 5 пятиугольных и т. д. Как и многие другие полученные им результаты, он лишь сформулировал это утверждение в письме к Блезу Паскалю (юрист по основной профессии, Ферма занимался математикой лишь в часы досуга). Частные случаи этой теоремы доказали Эйлер и Лагранж, а общее доказательство было дано в 1815 г. французским математиком О. Коши.
Наряду с комбинаторикой чисел греческие ученые занимались и отдельными вопросами геометрической комбинаторики — правильными и полуправильными многогранниками, составлением фигур из 14 частей особым образом разрезанного квадрата и т. д. Последнему вопросу была посвящена работа Архимеда «Стомахион».
Мистики, астрологи, каббалисты
Со II века до н. э. начинается сначала медленный, а потом все более быстрый упадок науки в эллинистических странах, отражавший общий кризис античного общества. Многие работы того времени были посвящены мистическим толкованиям чисел в духе пифагорейцев (например, «Арифметическая теология» неопифагорейца Никомаха, жившего в I - II веках н. э.). Большое развитие получили различные числовые суеверия и толкования, связанные с заменой букв соответствующими числами (греки обозначали числа с помощью букв — первые 9 букв алфавита обозначали числа от 1 до 9, следующие за ними — 10, 20, ..., 90, а последние 9 букв — 100, 200, ..., 900). Были «ученые», называвшиеся каббалистами, которые подвергали такому «анализу» слова Библии и других священных книг и делали на основе своих изысканий пророчества о будущем мира.
Во время богословских споров, начавшихся после победы христианства, старались получить из имен еретиков число 666 — ведь по Апокалипсису это было «звериное число», символ антихриста. Такие попытки предпринимались и позднее — лютеране пытались вывести число 666 из имени римского папы, а католики — из имени Мартина Лютера. В романе «Война и мир» Л. Н. Толстой описывает, как Пьер Безухов пытался вывести это число из имени Наполеона Бонапарта. Такого рода исследования при всей своей бесплодности давали толчок к дальнейшему развитию комбинаторики.
Наряду с каббалистами и мистиками комбинаторикой в это время занимались астрологи. Их интересовал вопрос о движении планет и их «влиянии» на судьбы людей. Особое значение придавали они сочетаниям планет — встречам различных планет в одном знаке Зодиака. Астролог бен Эзра в 1140 г. рассчитал количество сочетаний семи планет по две, по три и т. д. Он знал, что число сочетаний семи планет по две равно числу их сочетаний по пять, а число сочетаний по три равно числу сочетаний по четыре. Если обозначить эти утверждения в современных символах, то получатся равенства С27 =С57 и С37=С47.
В окончательном виде формулу для числа сочетаний получил живший в начале XIV века еврейский математик Леви бен Гершон, доказавший, что
Однако его работа, написанная на малодоступном большинству ученых древнееврейском языке, осталась почти незамеченной — вновь эту формулу вывел в начале XVII века французский математик П. Эригон.
Комбинаторика в странах Востока
В VIII веке н. э. начался расцвет арабской науки. Арабы перевели многие творения греческих ученых, изучили их, а затем продвинулись вперед в областях, мало привлекавших внимание греков, — в науке о решении уравнений, теории и практике вычислений и т. д. Решая вопрос об извлечении корней любой степени, арабские алгебраисты пришли к формуле для степени суммы двух чисел, известной под исторически неверным названием «бином Ньютона». По-видимому, эту формулу знал живший в XI — XII веках н. э. поэт и математик Омар Хайям. Во всяком случае, уже в XIII веке такую формулу приводит в своих трудах Насир ад-Дин ат-Туси, а в XV веке она была исследована Гиясэддином ал-Каши.
Судя по некоторым европейским источникам, восходящим к арабским оригиналам, для отыскания коэффициентов этой формулы брали число 10001 и возводили его во 2-ю, 3-ю, ..., 9-ю степени. Получалась таблица
100011 -10001
100012 - 100020001
100013 - 1000300030001
100014 - 10004000600040001
100015 - 100050010001000050001
100016 - 1000600150020001500060001
100017 - 10007002100350035002100070001
100018 - 100080028005600700056002800080001
100019 - 1000900360084012601260084003600090001
в которой подчеркнуты коэффициенты бинома Ньютона. Если опустить в этой таблице излишние нули и добавить сверху
100010 = 1, то получится треугольная таблица из биномиальных коэффициентов.
Арабские ученые знали и основное свойство биномиальных
коэффициентов, выражающееся формулой
Одновременно с арабами вычислением биномиальных коэффициентов занимались китайские математики. Они составили
к XIII веке н. э. таблицу таких чисел вплоть до п = 8, приведенную в книге алгебраиста Чжу Ши-дзе «Яшмовое зеркало». Имеются сведения, что астроном И Синь в VIII веке н. э. вычислил количество различных расположений фигур в игре, напоминавшей шахматы.
Интересовались сочетаниями и в Индии. Еще во II веке до н. э. индийцы знали числа С и тот факт, что сумма равна 2n. А в XII веке индийский математик Бхаскара написал книгу «Лилавати», в которой среди других вопросов математики изучаются и проблемы комбинаторики. Он писал о применениях перестановок к подсчету вариаций размера в стихосложении, различных расположений в архитектуре и т. д. Он дал также правила для отыскания числа перестановок и сочетаний нескольких предметов, при этом рассматривается случай, когда в перестановках есть повторяющиеся элементы.
Liber Abaci
Развитие торговли в XII с Востоком привело к проникновению в Европу арабской науки. Наиболее смелые и любознательные европейцы пробирались в находившуюся под владычеством арабов Испанию и знакомились там не только с творениями греческих ученых, но и с достижениями арабской и индийской научной мысли — алгеброй и десятичной системой счисления.
В арабских учебных заведениях получил образование и Леонардо — сын пизанского купца, торговавшего в Алжире. В своей книге “Liber Abaci”, вышедшей в 1202 г., Леонардо, получивший прозвище Фибоначчи, привел в систему всю арифметику арабов, некоторые сведения по геометрии Евклида и добавил к ним результаты своих изысканий. Труд Фибоначчи содержал и новые комбинаторные задачи, например, об отыскании наименьшего количества гирь, с помощью которых можно получить любой целый вес от 1 до 40 фунтов. Рассматривал Леонардо и отыскание целочисленных решений уравнений. В дальнейшем аналогичные задачи привели к отысканию количества натуральных решений систем уравнений и неравенств, которое может рассматриваться как одна из глав комбинаторики.
Но главной заслугой Леонардо перед комбинаторикой было то, что он сформулировал и решил задачу о кроликах. Со времен греческих математиков были известны две последовательности, каждый член которых получался по определенным правилам из предыдущих — арифметическая и геометрическая прогрессии. В задаче Леонардо появилась новая последовательность, члены которой были связаны друг с другом соотношением . Это была первая в истории науки формула, в которой следующий член выражался через два предыдущих. Подобные формулы получили название рекуррентных (от латинского recurrere — возвращаться). Метод рекуррентных формул оказался впоследствии одним из самых мощных для решения комбинаторных задач.
Игра в кости
Значительный толчок к развитию комбинаторики дали азартные игрыв. Наибольшее распространение получила игра в кости — два или три кубика с нанесенными на них очками выбрасывали на стол, и ставку брал выбросивший большую сумму очков. 
Мусульманские ученые писали про игру в нарды, в которой передвижения шашек определяются броском костей.
Опытные игроки, неустанно упражнявшиеся в бросании костей, заметили, что некоторые суммы очков выпадают часто, а другие — редко. Само слово «азартный» происходит от арабского «азар» — трудный, так называли редко выпадавшие комбинации костей. Пытаясь понять, в чем тут дело, составляли таблицы, показывавшие, сколькими способами можно получить то или иное число очков. На первых порах иногда допускалась ошибка — подсчитывали лишь число различных сочетаний костей, дававших данную сумму. Например, при бросании двух костей сумма 6 получается как 1 +5,2+ 4и З + 3, сумма 7 — из сочетаний 1 + 6,2 + 5иЗ+ 4,а сумма 8 — из сочетаний 2 + 6,3 + 5и4 + 4. Так как каждый раз получается три различных сочетания с данной суммой, то делался ошибочный вывод, что суммы очков 6, 7 и 8 должны выпадать одинаково часто. Но это противоречило опыту — 7 очков выпадали чаще. Дело в том, что при бросании двух костей сочетание 3 + 3 может быть получено единственным образом, а сочетание 3 + 4— двумя способами (3 + 4 и 4 + 3). Этим объясняется большая частота выпадения суммы 7.
Таким образом, оказалось, что надо учитывать не только сочетания очков, но и их порядок.
Более сложными оказались соответствующие исследованиядля трех костей. Здесь при учете порядка костей оказывается 3 6 =216 различных комбинаций, а без учета порядка — лишь 56.
Этими вопросами занимались такие известные итальянские математики XVI века, как Д. Кардано, Н. Тарталья и др. Наиболее полно их исследовал в XVII веке Галилео Галилей, но его рукопись оставалась неопубликованной до 1718 г.
Игрок и ученые
Одним из самых азартных игроков в кости в XVII веке был шевалье де Мере, непрерывно изобретавший новые виды состязаний. Например, он предложил, что будет бросать четыре кости и брать выигрыш лишь в случае, когда хотя бы одна из них откроется на шести. Однако вскоре его партнеры отказались от участия в такой игре — шевалье чаще выигрывал, чем проигрывал. Тогда де Мере придумал новый вариант — он бросал несколько раз пару костей и брал выигрыш, если хотя бы раз выпадали две шестерки. Надо было лишь определить, сколько следует сделать бросков, чтобы игра была ему столь же выгодна, как и первая. Шевалье решил, что надо бросать кости 24 раза. Ведь при четырех бросках одной кости шестерка выпадала более чем в половине случаев, а так как вторая кость дает шесть вариантов выпадения, то и надо умножить 4 на 6. Рассуждение казалось безукоризненным, но опыт не подтвердил надежд де Мере — теперь он стал чаще проигрывать, чем выигрывать.
Другой проблемой для де Мере была задача о разделе ставки. Проблема состояла в следующем: «матч» ведется до шести выигранных партий; он был прерван, когда один игрок выиграл 5 партий, а другой — 4; как разделить ставку? Было ясно, что раздел в отношении 5:4 несправедлив.
Де Мере обратился за разъяснениями к двум крупнейшим математикам Франции XVII века — Блезу Паскалю и Пьеру Ферма. Разбираясь в этих и других задачах, поставленных перед ними де Мере, они сформулировали и доказали первые теоремы комбинаторики и теории вероятностей. А задачу о разделе ставки Паскаль решил в общем случае, когда одному игроку остается до выигрыша r партий, а второму s партий. Другое решение задачи дал Ферма.
Новая ветвь математики
Работы Паскаля и Ферма ознаменовали рождение двух новых ветвей математической науки — комбинаторики и теории вероятностей. Если до них комбинаторные проблемы лишь затрагивались в общих трудах по астрологии, логике и математике, а большей частью относились к области математических развлечений, то уже в 1666 г. Готфрид Вильгельм Лейбниц публикует «Диссертацию о комбинаторном искусстве», в которой впервые появляется сам термин «комбинаторный.Диссертация Лейбница должна была стать лишь началом большой работы, о которой он часто упоминал в своих письмах и печатных трудах и для которой делал в своих записных книжках многочисленные заметки. Из них видно, что Лейбниц планировал для комбинаторики все новые и новые приложения: к кодированию и декодированию, играм, статистике, теории наблюдений. Под комбинаторикой Лейбниц понимал примерно то, что мы теперь называем дискретной математикой. К области комбинаторики Лейбниц относил и «универсальную характеристику» — математику суждений, т. е. прообраз нынешней математической логики.
Проекты Лейбница казались несбыточными здравомыслящим математикам его времени, но после создания компьютеров многие планы Лейбница стали претворяться в жизнь, а дискретная математика выросла в своем значении настолько, что начала соперничать с классическим математическим анализом.
В 1713 г. племянник Якоба Бернулли (скончавшегося в 1705 г.) Николай опубликовал часть II книги Якоба Бернулли «Ars conjectandi» («Искусство предположений»), в которой указывались формулы для числа размещений из п элементов по k, выводились выражения для степенных сумм и т. д. Замечательные достижения в области комбинаторики принадлежат одному из величайших математиков XVIII века Леонарду Эйлеру, швейцарцу, прожившему почти всю жизнь в России, где он был членом Петербургской академии наук. Основные работы Эйлера в области науки посвящены математическому анализу, в котором он проложил новые пути, создал целый ряд новых областей и подвел итоги исследованиям в других областях. Но у Эйлера хватало времени размышлять и о задачах, которые, казалось бы, не заслуживали его внимания, — о том, можно ли обойти мосты в Кенигсберге (ныне Калининграде) так, чтобы не побывать дважды на одном и том же мосту; можно ли поставить 36 офицеров из 6 разных полков так, чтобы в каждой шеренге и каждой колонне было по одному офицеру каждого воинского звания из каждого полка; сколькими способами можно разбить данное число на слагаемые и т. д. Но, странное дело, работа о мостах явилась зерном, из которого впоследствии выросли топология и теория графов, задача об офицерах оказалась сейчас связанной с планированием экспериментов, а методы, использованные при решении задачи о разбиении чисел, после длительного и сложного пути развития превратились в науку об интегральных преобразованиях, применяемую для решения уравнений математической физики.
После работ Паскаля и Ферма, Лейбница и Эйлера можно было уже говорить о комбинаторике как о самостоятельной ветви математики, тесно связанной с такими областями науки, как теория вероятностей, учение о рядах и многими другими. В конце XVIII века немецкий ученый Гинденбург и его ученики сделали даже попытку построить общую теорию комбинаторного анализа. Однако она не увенчалась успехом — в то время еще не было накоплено достаточного количества важных и интересных задач, которые могли бы дать необходимый фундамент для такой теории.
В XIX веке в ходе исследований по комбинаторике стали прослеживаться связи этой теории с определителями, конечными геометриями, группами, математической логикой и т. д.
Комбинаторика и шифры
Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали все более и более сложные шифры, а секретные службы других государств пытались эти шифры разгадать.
Комбинаторные методы применял для шифрования еще итальянский ученый XVI века Джовани Баттиста делла Порта. Они были основаны на циклической перестановке букв. Русские дипломаты в XV - XVI веках применяли «тарабарскую грамоту», в которой все гласные буквы оставались неизменными, а согласные заменялись друг на друга по такой схеме:
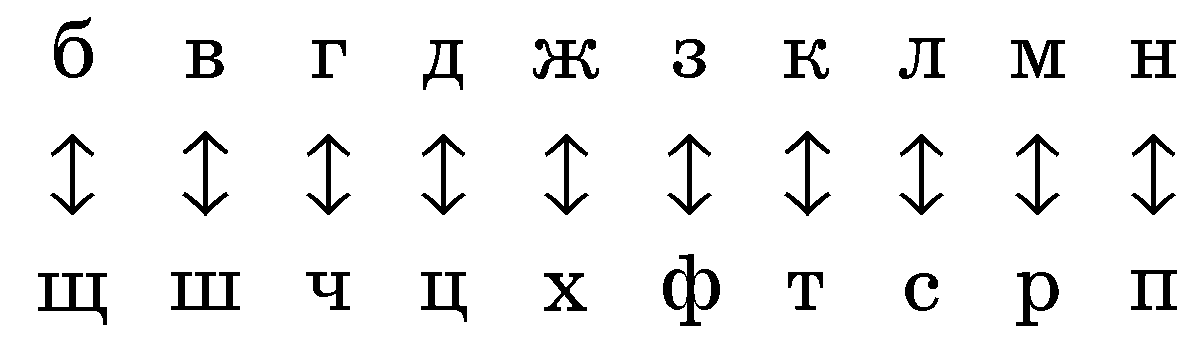
(в первой строке согласные идут в обычном порядке, а во второй строке — в обратном). Однако такие шифры легко разгадывались по характерным сочетаниям букв. Поэтому стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т. д.
Для кодирования и расшифровки привлекались математики. Еще в конце XVI века расшифровкой переписки между противниками французского короля Генриха III и испанцами занимался один из создателей современной алгебры Франсуа Виета. А в Англии XVII века монархистские заговорщики поражались быстроте, с которой Кромвель проникал в их замыслы. Монархисты считали шифры, которыми они пользовались при переписке, неразгадываемыми, и считали, что ключи к ним были выданы кем-то из участников заговора. И лишь после падения республики и воцарения Карла II они узнали, что все их шифры разгадывал один из лучших английских математиков того времени, профессор Оксфордского университета Уоллис, обладавший исключительными комбинаторными способностями. Он назвал себя основателем новой науки «криптографии» (тайнописи).
Анаграммы
До XVII столетия почти не было научных журналов. Ученые узнавали о трудах своих коллег из книг или из частных писем. Это создавало большие трудности при опубликовании новых результатов — ведь печатание книг занимало целые годы, а написать о своем открытии в частном письме было рискованно — не ровен час, кто-нибудь присвоит достижение, и поди доказывай, что он узнал это из полученного письма, а не сам придумал. А могло случиться, что получатель письма долго думал над тем же вопросом, нашел его решение, и письмо действительно ничего нового ему не открыло — он сам собирался написать коллеге аналогичное сообщение.
Из-за этого часто возникали споры о приоритете. Еще в конце XVII столетия шли долгие споры о приоритете между Ньютоном и Лейбницем (о том, кто первый создал дифференциальное и интегральное исчисления), между Ньютоном и Гуком (кто первый сформулировал закон всемирного тяготения) и т. д.
А в древности Архимеду пришлось даже пуститься на хитрость. Когда некоторые александрийские ученые присвоили себе его результаты, о которых узнали из полученных от него писем, он написал им еще одно письмо. В нем содержались совершенно замечательные формулы для площадей и объемов некоторых фигур. Александрийцы снова сказали, что эти формулы они давным-давно знают, и ничего нового им Архимед не сообщил. Но тут выяснилось, что Архимед поймал их в ловушку — сообщенные в письме формулы были неверными!
Для того чтобы и приоритет обеспечить, и не допустить преждевременной огласки достигнутых результатов, ученые в краткой фразе формулировали суть открытия, а потом переставляли в ней буквы и посылали письмо с переставленными буквами своим коллегам. Такие тексты с переставленными буквами называются анаграммами. Например, слова «Москва» и «смоква» — анаграммы. Когда же печаталась книга с подробным изложением результата, в ней давалась расшифровка анаграммы.
К анаграммам прибегали и в политических спорах. Например, после убийства французского короля Генриха III из имени его убийц![]() (брат Жак Клеман) составили анаграмму
(брат Жак Клеман) составили анаграмму ![]() (меня создал ад). Противники короля не остались в долгу и из его имени
(меня создал ад). Противники короля не остались в долгу и из его имени ![]()
![]() (Анри де Валуа) составили анаграмму
(Анри де Валуа) составили анаграмму ![]() (Иродова мерзость).
(Иродова мерзость).
Когда Христиан Гюйгенс открыл кольцо Сатурна, он составил анаграмму
aaaaaaa, ccccc, d, eeeee, g, h, iiiiiii, lll, mm,
nnnnnnnnn, oooo, pp, q, rr, s, ttttt, uuuuu.
Буквы в ней можно поставить в таком порядке, что получится текст «Annulo cingitur tenui, piano, nusquam cohaerente, ad eclipticam inclinato» («окружен кольцом тонким, плоским, нигде не подвешенным, наклонным к эклиптике»).
Однако не всегда анаграммы позволяли сохранять тайну. Когда тот же Гюйгенс открыл первый спутник Сатурна (Титан) и нашел, что время его обращения вокруг планеты равно 15 дням, он составил по этому поводу анаграмму и послал своим коллегам. Однако один из них, уже упоминавшийся Уоллис, большой мастер в расшифровке тайнописи, разгадал эту анаграмму и составил по этому поводу свою анаграмму, которую послал Гюйгенсу. Когда ученые обменялись разгадками анаграмм, то получилось так, что будто бы Уоллис еще до Гюйгенса сделал то же самое открытие. Потом Уоллис признался, что он пошутил, чтобы доказать бесполезность анаграмм в деле тайнописи. Гюйгенс, однако, хотя и сам был большим любителем и знатоком комбинаторики, не оценил этой шутки и рассердился...
Иероглифы и клинопись
Навыки в разгадке сложных шифров помогли ученым, когда археологи стали откапывать камни и черепки с таинственными знаками — письменностью, замолкшей несколько тысячелетий тому назад. Одним из самых замечательных успехов в деле расшифровки таких текстов было прочтение французским филологом Жаном Франсуа Шампольоном иероглифов, которыми писали египтяне еще до того, как возникла наука у древних греков.
У Шампольона были предшественники — шведский археолог Д. Окерблад и английский физик Т. Юнг, которые подвергли египетские тексты комбинаторному анализу. В их руках были «билингвы» — надписи, сделанные одновременно на египетском и греческом языках. Сравнивая оба текста и выясняя повторяемость групп знаков, Окерблад опознал некоторые знаки так называемого демотического письма — поздней стадии развития египетской письменности. А создатель волновой оптики Томас Юнг любил на каникулах отдохнуть от размышлений на физические темы и занимался то каллиграфией, то составлением алфавитов иностранных языков, то... танцами на слабо натянутом канате, — по мнению Юнга все, что мог сделать один человек, мог повторить другой. В 1814 г. он взял с собой на каникулы древнеегипетский папирус и попробовал прочесть его. Не имея должной филологической подготовки, путем лишь комбинаторного исследования текста он получил интересные результаты, а затем попробовал читать иероглифы. Кое-каких успехов он добился и здесь, но сказалось недостаточное знание языков — он искал иероглифы не только для согласных, но и для гласных букв, а в египетском письме гласные опускались. Лишь Шампольону, сочетавшему незаурядный комбинаторный дар с глубочайшим знанием филологии, удалось прочесть иероглифы.
Сложность задачи, стоявшей перед Шампольоном, усугублялась тем, что не были известны ни язык надписей, ни смысл знаков. Однако, выделив знаки, которые в греческом тексте обозначали имена царей, Шампольон обнаружил, что некоторые знаки в именах фараонов Птолемея и Клеопатры совпадают. Так были найдены звучания иероглифов, означавших буквы «п» и «л» (до этого места дошел и Юнг). А затем Шампольон распознал имена римских императоров Тиберия и Траяна, древних фараонов Рамсеса и Тутмеса — ключ к чтению иероглифов, утерянный несколько тысячелетий тому назад, был вновь обретен.
Прочтение забытых письменностей было торжеством комбинаторного метода, основанного на наблюдениях над текстом, на сопоставлении повторяемости комбинаций слов и грамматических форм в сочетании с соображениями, связанными с назначением надписи, временем и условиями ее составления и т. д.
Еще теснее связана с комбинаторикой история расшифровки клинописных надписей. Историкам удалось установить, что эти надписи были сделаны в эпоху Ахеменидов, правивших в Иране два с половиной тысячелетия тому назад. Были сделаны и предположения о языке надписей. А потом комбинаторный анализ текста вскрыл часто повторявшуюся группу из семи знаков. Иногда эта группа повторялась дважды подряд с небольшими изменениями. И датский ученый Мюнтер решил, что эта группа означает слово «царь», а повторенная дважды — «царь царей». Но узнать звучание этих знаков Мюнтер не сумел. Это сделал молодой немецкий учитель Гротефенд. Любитель различных головоломок и тайнописи, он однажды (как гласит предание, после веселого вечера в дружеской компании) заключил пари, что расшифрует клинопись. Анализируя сочетания знаков около титулов «царь» и «царь царей», Гротефенд обнаружил, что некоторые из них встречаются в разных позициях. Отсюда был сделан вывод, что это имя царя, которое в иной позиции означает «сын царя такого-то». Это позволило опознать и группу знаков для слова «сын». В одном месте после этой группы знаков не стояло слово «царя». Значит, решил Гротефенд, царь, о котором идет здесь речь, не был сыном царя — это был сам основатель династии Дарий, сын Гистаспа. А так как Дарий был отцом Ксеркса, то у Гротефенда были в руках звуковые значения для знаков, входивших в имена «Гистасп», «Дарий», «Ксеркс» — начало расшифровки клинописи было положено!
Комбинаторика позволила прочесть и крито-микенское линейное письмо.
Первые прочные основы дешифровки этой письменности заложила Алиса Д. Кобер, защитившая в 1932 г. докторскую диссертацию по математике в Колумбийском университете. Наряду с исследованиями по чистой математике она много сил уделяла расшифровке древних письменностей. Изучив знаки критского письма, Кобер установила, что это письмо является слоговым. Далее она заметила, что в исследуемых текстах
некоторые слова встречаются в трех различных формах, отличающихся друг от друга несколькими последними знаками, по-видимому, падежными окончаниями. А дальше она начала составлять «лингвистические уравнения» для слогов, позволившие ей найти слоги с одинаковыми согласными, но разными гласными, и одинаковыми гласными, но разными согласными. В результате Кобер получила координатную сетку, в которой вместо осей координат стояли номера гласных и согласных букв. У этой сетки был лишь один недостаток — никто не знал, какие именно гласные и согласные образуют эту систему координат.
Лишь через два года после смерти исследовательницы молодой английский архитектор Майкл Вентрис, расширяя ее координатную сетку, попробовал угадать значения некоторых гласных — число гласных меньше числа согласных, и перебор лучше начинать с них. Одна из попыток оказалась удачной — текст заговорил на языке, весьма напоминавшем греческий. Но это не был классический греческий язык «Илиады» и «Одиссеи», а греческий язык более ранней эпохи. Вентрису помог завершить расшифровку видный знаток раннего греческого языка Чэдвик. Используя имена царей и списки географических названий, исследователи расшифровывали один слог за другим. А потом началась цепная реакция дешифровки — три десятка знаков получили свое значение.
Это был полный триумф комбинаторного подхода, основанного на следующем положении, сформулированном Вентрисом: «При попытке дешифровать документы на неизвестном языке, написанные неизвестным письмом, первый шаг состоит в установлении тех фактов, которые сами даются в руки при рассматривании имеющихся в распоряжении документов. Второй шаг состоит в том, что исследователь путем тщательного анализа и логической дедукции выявляет, какие выводы можно сделать из этих основных фактов».
При расшифровке буквенной письменности оказывается весьма важным отделение знаков, обозначающих гласные буквы, от знаков, обозначающих согласные буквы. И здесь на помощь приходит комбинаторика. Филолог В. В. Шеворошкин установил метод, основанный на комбинаторном сравнении частоты различных сочетаний пар знаков. Хорошо известно, что в языках гласные и согласные определенным образом чередуются друг с другом. Это позволяет разделить все знаки на две группы так, что, как правило, знаки одной группы перемежаются в тексте знаками другой группы. Тогда знаки, входящие в меньшую группу, будут обозначать гласные, а входящие в большую группу, — согласные. Этот метод дал исследователю ключ к чтению карийских надписей.
ПЕРЕСТАНОВКИ
Пусть имеется п объектов, неважно каких, лишь бы все они различались между собой: книги, детские кубики или музыканты крыловского «Квартета». Мысленно расставим их в ряд и такое упорядоченное расположение объектов назовём перестановкой. Попытаемся ответить на вопрос: сколько всего возможно перестановок из п предметов? Число перестановок обозначают Рп, подчёркивая тем самым, что оно зависит от количества предметов п.
Перестановки -- комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.
Попытаемся найти Рп сначала для небольших п. Если п = 1, т. е. имеется один-единственный предмет, то существует и один-единственный способ его расстановки. Поэтому Р1 = 1. Возьмём п = 2. Сразу понятно, что Р2 = 2, поскольку два предмета (назовём их А и Б) можно расставить двумя различными способами: АБ и БА. Попробуем рассуждать несколько иначе: первый предмет (А) установим неподвижно, а второй (Б) будем «прилаживать» к нему. Безусловно, объект Б можно поставить либо спереди, либо сзади от А, следовательно, число перестановок Р2 вдвое больше, чем Р1 , т.е. Р = Р1 •2 = 1 • 2. Добавим теперь третий предмет В. К каждой из перестановок двух объектов А и Б можно пристроить третий предмет тремя различными способами: поставить его спереди, между ними либо сзади. Перестановка АБ, таким образом, порождает три перестановки: ВАБ, АВБ и АБВ, перестановка БА — также три: ВБА, БВА и БАВ, и все получившиеся шесть перестановок — разные. Отсюда Р3 = P2 • 3 = 1 • 2 • 3.
Вообще, из каждой перестановки п -1 предметов можно получить п дополнительных перестановок, добавляя n-й предмет либо спереди, либо сзади, либо между имеющимися предметами (между п - 1 предметами существует п - 2 промежутка; 1 + 1+n-2 — вот и выходит ровно п). Стало быть, при переходе от п - 1 к п предметам количество перестановок увеличивается в п раз. Поэтому общая формула будет такой: .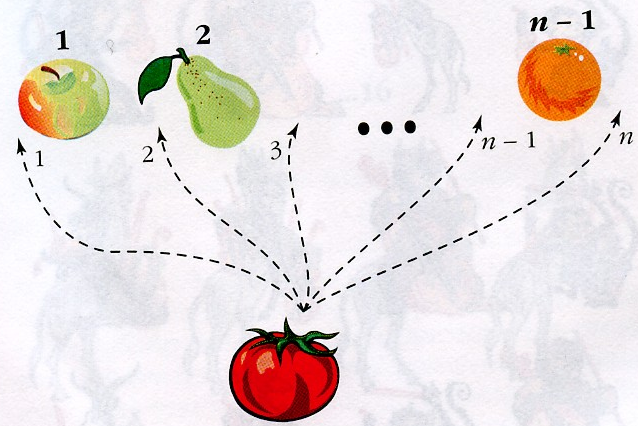
Из каждой перестановки п - 1 предметов можно получить п перестановок п предметов, добавляя п-й предмет либо спереди, либо сзади, либо между меющимися предметами.
Восклицательным знаком (в математике он называется факториалом) принято обозначать произведение всех натуральных чисел от 1 до n включительно.
Выше приведён не просто вывод формулы, но одновременно способ того, как получить все возможные перестановки. Надо отметить, что он далеко не единственный. Например, все перестановки можно получить из начальной, поочерёдно меняя местами соседние объекты:
АБВ →АВБ →ВАБ → ВБА →БВА → БАВ.
Правило суммы (или сложения): Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать объект А или объект В можно выбрать (m+n) способами.

Правило произведения (или умножения): Если некоторый объект А может быть выбран из совокупности объектов m способами, и после такого выбора объект В может быть выбран n способами, то пару объектов А и В в указанном порядке можно выбрать (m n) способами.
Решение задачи о квартете
Четыре горе-музыканта из басни Крылова долго пересаживались с места на место. В ходе этого «творческого поиска» Осёл внёс предложение: «Мы, верно, уж поладим, коль рядом сядем». Попробовали — не помогло. Но в ряд-то можно сесть по-разному! Давайте определим число возможных перестановок. Здесь п = 4, поэтому способов «усесться чинно в ряд» имеется Р4 = 4! = 1 2 3 4 = 24.
Зеркально-симметричные перестановки
Добавим, что для решения некоторых задач приходится применять идею перестановок не в «чистом» виде, а с поправками. Допустим, главный фактор, влияющий на качество игры, — это соседи каждого музыканта, и не важно, кто из них справа, а кто слева. При таком условии перестановка «Мартышка, Осёл, Козёл, Мишка» эквивалентна зеркально-симметричной: «Мишка, Козёл, Осёл, Мартышка». Понятно, что в этом случае все Р4 вариантов разбиваются на пары равнозначных перестановок. И если из каждой пары оставить по одной перестановке, то общее число различающихся вариантов будет 12.
Теперь представим, что музыканты сели не в ряд, а по кругу. В этом случае можно рассуждать так: в каждом из вариантов пронумеруем всех участников по часовой стрелке, начиная, скажем, с Осла. В различных перестановках каждый музыкант, конечно, должен иметь разные номера. Только у одного из них — Осла — будет постоянный номер 1. Значит, осталось пронумеровать различными способами только троих. Поэтому здесь число возможных перестановок — Р3 = 3! = 6.
Перестановки с повторениями
Есть особый (и очень важный!) вид перестановок — перестановки с повторениями. В них среди прочих участвуют предметы, неразличимые между собой, — «близнецы». Замена одного «близнеца» другим не приводит к новой расстановке. Предположим, что, отчаявшись, наши музыканты решили создать вместо квартета симфонический оркестр. Для этого Мартышка привела с собой ещё 15 Мартышек, Осёл — ещё 20, Ослов, Козёл — 10 Козлов, лишь Мишка поленился и остался в одиночестве. Выясним, сколькими способами можно рассадить их в ряд.
Возьмём любую произвольную расстановку всех 16 + 21 + 11 + 1= 49 музыкантов. Если бы «близнецов» в их числе не оказалось, то перестановок было бы 49!. Но вот среди них появилось 16 одинаковых Мартышек. Не трогая остальных зверей, а меняя местами лишь Мартышек всеми возможными способами (а их будет 16!), получим вроде бы новые перестановки, но теперь уже неразличимые. То есть каждые 16! старых перестановок преобразуются в одну новую и общее число перестановок уменьшается в 16! раз. Очевидно, та же история и с Ослами, и с Козлами (лишь Медведь по-прежнему один). В итоге количество перестановок окажется равным
Медведя не учитывали, но, дабы не нарушать единообразия, добавим и его, т. е. поделим указанное выражение ещё на 1! = 1:
Чтобы отличить перестановку с повторениями от обычной, над буквой Р ставится горизонтальная черта.
Можно получить и общую формулу для случая, когда имеется п групп «близнецов», состоящих соответственно из k1 ,k2 ,… , kn неразличимых предметов:
Множество факториалов в этой формуле может вызывать трудности. Но в комбинаторике фактори- ал — частый гость, даже хозяин. К сожалению, на калькуляторе функция «факториал» обычно отсутствует, поэтому при практических расчётах приходится последовательно умножать натуральные числа. Занятие довольно трудоёмкое — попробуйте, например, вычислить 49!. Однако, когда не требуется абсолютной точности, для больших п можно с успехом использовать формулу, которую вывел в XVIII в. шотландский математик Джеймс Стирлинг:
Она примечательна не только высокой точностью (уже при и - 10 погрешность менее 1 %) , но и неожиданным присутствием двух замечательных чисел: числа Эйлера е = 2,71828... и числа π = 3,14159… А произвести вычисления по формуле Стирлинга на хорошем калькуляторе не составляет труда.
РАЗМЕЩЕНИЯ
Иногда бывает нужно из п имеющихся различных объектов отобрать произвольные т штук (т ≤ п) и расположить их в некотором порядке. Каждое такое упорядоченное расположение называется размещением. Сколько существует размещений при заданных п и т? Оказывается, ответ можно дать, основываясь на знании перестановок.
Размещения -- комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.
Обозначим искомое число Аnm . Сначала возьмём любую перестановку всех n объектов и рассмотрим первые т из них. Они образуют размещение т объектов из п имеющихся, тогда как последние п - т объектов совершенно не влияют на это размещение, как их ни переставляй. Но эти п - т «хвостовых» объектов могут быть переставлены Рп-т способами. Значит, каждому размещению можно «пришить» Рп-т различных «хвостов», что порождает столько же перестановок всех п объектов. Общее число перестановок всех объектов Рп в таком случае равно произведению искомого Аnm числа и Рn-m:
Отсюда
Есть ли у нуля факториал?
Сколькими способами можно выбрать 0 объектов из п имеющихся, или, другими словами, сколькими способами можно не выбрать ни одного объекта? Вопрос, конечно, странный, но формально получается
Пожалуй, это логично: есть единственный способ не выбрать ни одного объекта из п имеющихся — ничего не делать.
Второй вопрос: сколькими способами можно сделать упорядоченный выбор из п объектов... всех п? Поступаем так: выбираем любой объект, рядом с ним размещаем второй, потом тре-тий и т. д. Получается обыкновенная перестановка всех п объектов, и число таких перестановок Рп = п!. С другой стороны, согласно найденной формуле, это же число равняется
Появилось новое выражение 0! (факториал мы определяли только для натуральных чисел). Предположим, что 0! — это какое-то неизвестное число, и найдём его из равенства Ann =P n . Тогда =n!, откуда 0! = 1, т. е. факториал нуля равен единице (хотя казалось, что это непременно должен быть нуль). Факториал нуля возникает в самых разных комбинаторных задачах, но везде и всегда его принимают равным единице.
Размещения с повторениями
Помимо обычных размещений бывают и размещения с повторениями (точно так же, как перестановки). Пусть имеется п различных объектов. Выберем из них т штук, действуя по следующему принципу. Возьмём любой, но не будем устанавливать его в какой-то ряд, а просто запишем под номером 1 его название, сам же объект после этого вернём к остальным. Затем опять из всех п объектов выберем один (в том числе, возможно, и тот, который был только что взят), запишем его название, пометив номером 2, и снова вернём объект обратно. И так далее, пока не получим т названий. размещения с повторениями обозначаются .
Каждый предмет после «использования» возвращается обратно и может быть «использован» повторно
Определить это число несложно. На первом месте в списке может находиться любой из п объектов, на втором — тоже любой, и на третьем, и на четвёртом... в общем, на каждом. Поэтому число размещений с повторениями выражается формулой
Здесь допустим случай, когда т п, т. е, выбранных объектов больше, чем их всего имеется. Это неудивительно: каждый объект после «использования» возвращается обратно и может быть «использован» повторно.
Решение задачи о паспортах
Нужно определить, сколько может быть паспортов советского образца с различными сериями и номерами, если зафиксировать римские цифры серии. Остаются две русские буквы и шесть арабских цифр. Рассмотрим буквы и цифры отдельно.
Буквы. В русском алфавите 33 буквы. Нам нужно выбрать любые две, при этом они могут оказаться и одинаковыми. Следовательно, имеет место размещение с повторениями, где п = 33 и т = 2: = ЗЗ2 =1089.
Цифры. Здесь выбирается (и опять с повторениями) т = 6 цифр из n = 10 возможных. Для этого есть = 106 способов.
Итог: поскольку каждую пару букв можно соединить с любой шестёркой цифр, то возможно существование • - ЗЗ2 •106 = = 1 089 000 000 паспортов, имеющих одни и те же римские цифры серии, — больше миллиарда! Ну а если потребовать, чтобы в каждом номере и буквы, и цифры были различными, — сколько тогда получится паспортов? Здесь вместо размещений с повторениями нужно использовать обычные размещения. Поэтому ответ таков:
В результате число значительно уменьшилось.
СОЧЕТАНИЯ
В некоторых задачах по комбинаторике не имеет значения порядок расположения объектов в той или иной совокупности. Важно лишь то, какие именно элементы её составляют. К примеру, представим себе школьный класс, который пришёл в спортзал. Школьники могут выстроиться в шеренгу, а бегать где попало, прыгать, кувыркаться, стоять на голове, лазать по канату — всё равно они останутся тем же самым множеством учеников класса. Теперь часть из них переведём в соседнее помещение, где им также дозволяется бегать, прыгать и т. д. Такая выборка элементов, при которой их порядок совершенно неважен, называется сочетанием.
Сочетания -- комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом.
Число всевозможных сочетаний из п элементов по т обозначается Сnm Найдём это число.
Будем основываться на том, что нам известно: на размещениях и перестановках. Сначала из п элементов выделим какие-либо т элементов с учётом очерёдности выбора. Это — размещение, и число таких размещений Anm . Очевидно, что различные размещения, в которые входят те же объекты, но в ином порядке, будут соответствовать одному сочетанию (ведь в сочетании порядок роли не играет). Другими словами, любая перестановка выбранных m элементов порождает то же самое сочетание. Но таких перестановок Рт. Поэтому число сочетаний из п элементов по m в Рm раз меньше числа размещений, т. е.
Следует обратить внимание на своеобразную симметрию этой формулы: если заменить m на п - m, получится то же самое, только факториалы в знаменателе поменяются местами. Отсюда следует замечательное свойство сочетаний:
Объясняется это можно следующим образом: каждому сочетанию из т отобранных элементов всегда соответствует сочетание из п - т оставшихся. Так что можно с самого начала говорить не о выделении т объектов из n, а о разбиении множества исходных п элементов (например, тех же школьников) на две части — поmиn-m в каждой (m человек — в один зал, а п - т — в другой).
Попытаемся теперь ответить на следующий вопрос: сколькими способами п школьников могут разделиться по t залам так, чтобы в первом зале оказалось m1 школьников, во втором тг и т. д., где т1 + тг + ... + mt=n? Обозначим искомое число через . Как его получить? Сначала из общего количества п школьников выделим m1 потом из п - т1 оставшихся т2 и т. д., следовательно,
Удивительно: хотя не рассматривались никакие перестановки, все школьники были заведомо разные, тем не менее выведена формула, точно повторяющая формулу для числа перестановок с повторениями. Дело в том, что данную задачу можно трактовать двояко. С одной стороны, мы распределяем отличающихся друг от друга школьников по залам. Тогда получаются сочетания. Но опишем ситуацию по-другому: мы как бы распределяем среди школьников билеты в разные залы. Причём билеты в один зал неотличимы друг от друга. Это уже перестановки (билетов среди построенных в ряд школьников) с повторениями.
Задача о Лотто-Миллион
Сколько карточек Лотто-Миллион нужно купить и заполнить, чтобы на них оказались все комбинации по 6 номеров из 49 возможных? Количество карточек равно числу сочетаний из 49 элементов по 6, т. е.
а это составляет почти 14 млн. Можно сделать вывод : для реализации подобной идеи уже надо быть миллионером! Но и в этом случае разбогатеть будет трудно, поскольку выигрыш не фиксирован и в каждом тираже на призовой фонд отводится лишь часть собранной от продажи билетов суммы.
Заполненная карточка Лотто-Миллион
Допустим, мы купили С496 карточек и все их по-разному заполнили. После тиража 6 счастливых номеров окажется только на одной из них. Но в Лотто-Миллион выигрывают и карточки с совпадением 5 и даже 4 номеров. Сколько их?
Если на карточке угадано 5 номеров, это значит, что из 6 выпавших номеров здесь могут быть вычеркнуты любые 5, а из остальных 43 — лишь 1. Поэтому число способов угадать 5 номеров равно . Точно так же карточек с совпадением 4 номеров будет . Наконец, на карточках не окажется ни одного выпавшего номера.
Сочетания с повторениями
И перестановки, и размещения могут быть с повторениями. Имеет смысл говорить и о сочетаниях с повторениями. Из множества, содержащего n предметов, нужно взять один произвольный, занести его в список, после чего вернуть обратно. Затем точно так же выбрать ещё один объект и т. д., пока в списке не окажется m наименований (среди них могут быть и одинаковые). Принципиальное отличие от размещений с повторениями заключается в том, что в данном случае элементы списка не нумеруются. Например, списки «А, Б, А, Г» и «Б, Г, А, А» считаются одинаковыми. Найдём число сочетаний с повторениями из n элементов по m. Произвольно пронумеруем элементы исходного множества числами от 1 до n. Пусть в какое-то из полученных сочетаний вошло k элементов под номером 1, k2 элементов под номером 2, ..., kn элементов под номером n. Что можно сказать обо всех этих числах ki ? Cумма (ведь в списке всего m объектов!).
Теперь изобразим это сочетание в виде цепочки из нулей и единиц. Единица здесь будет обозначать каждый отдельный элемент сочетания, а нуль — символизировать границу между группами элементов, соответствующих соседним ki . Если некоторое ki = 0, т. е. элементов с номером i в списке нет, то в соответствующем месте цепочки окажутся два «пограничных» нуля подряд.
Итак, записываем: сначала k1 единиц, затем один нуль, после этого k2 единиц и снова нуль… kn-1 единиц и опять нуль, наконец, kn единиц - и всё.
Поскольку сумма всех ki равна m, в построенной цепочке содержится m единиц. Нулей же n - 1. Так что вся цепочка состоит из n +m - 1 цифр.
Подведём итог. Каждому возможному списку поставлена в соответствие некоторая цепочка из нулей и единиц длиной n +m - 1. При этом если два списка одинаковы, то и цепочки получатся одинаковыми. Верно и обратное: каждой цепочке соответствует определённый список. Например, цепочка 1111001010 говорит нам, что в списке — четыре элемента номер 1, ни одного элемента номер 2, по одному элементу номер 3 и 4 и ни одного элемента номер 5. Таким образом, задача свелась к поиску ответа на вопрос: сколько можно составить различных цепочек длиной n +m – 1 из m единиц и n- 1 нулей? А это не что иное, как число перестановок с повторениями из m нулей и n- 1 единиц, т. е. . Поэтому
Итак, формулы для перестановок, размещений и сочетаний (с повторениями и без) обнару-живают тесную связь между основными понятиями комбинаторики. Эти формулы составляют своего рода азбуку комбинаторики, поскольку на них основано решение большинства школьных комбинаторных задач
БИНОМ НЬЮТОНА
В алгебре довольно часто приходится возводить в степень двучлен а + b. Недаром каждый школьник заучивает наизусть формулы квадрата и куба суммы двух чисел. Аналогичная формула, но уже для произвольного п 0 называется биномом Ньютона, хотя и была известна задолго до него. ( Слово «бином» в переводе с латыни означает «двучлен».) Формула эта имеет прямое отношение к комбинаторике.
Для удобства в выражении (а + b)n вынесем bn за скобки и обозначим а/b через х. Поучается bn (x+1)n. На время забудем про множитель bп и будем искать формулу для (х + 1)n. После раскрытия скобок перед нами предстанет многочлен n-й степени. Нужно только определить коэффициенты при различных степенях х.
Выпишем произведение из n скобок (x+1):
Теперь раскроем скобки, но при этом не будем приводить подобные члены. Например:
и т. д.
Естественно, результат представляет собой сумму каких-то степеней х (в том числе и нулевой, т. е. 1).
Наконец, соберём все x по одинаковым степеням и получим многочлен n-й степени уже в привычном виде. Ясно, что коэффициент при хт будет равен количеству слагаемых хт в первоначальном, неприведённом виде. Сколько их? Ещё не зная, как ответить на этот вопрос, мы уже чувствуем, что перед нами комбинаторная задача...
Биномиальные коэффициенты и сочетания
После перемножения п скобок (х + 1) любая появившаяся степень х возникла как произведение п сомножителей — по одному от каждой скобки. Но все сомножители равны либо х, либо 1. Для появления т-й степени х необходимо, чтобы при перемножении ровно из т скобок были взяты сомножители х, а из остальных п - т скобок — 1. Сколькими способами можно выбрать т объектов (в данном случае скобок) из п возможных?
Таблица биномиальных коэффициентов из книги Якоба Бернулли «Искусство предположений». 1713г.
Или, другими словами, каково число сочетаний из п элементов по т? Ответ : Сnm . Итак, раскрыв все скобки, получим Сnm слагаемых, равных xm, и, значит, после приведения подобных членов коэффициент при xm равен Сnm . Поэтому
Так как числа Сnm являются коэффициентами в формуле бинома Ньютона, они называются биномиальными коэффициентами. Попробуем выписать формулы бинома (х + 1)n для некоторых конкретных значений х, например для x=0, ±1,±2, ±1/2.
Нетрудно вывести подобную формулу и для (а + b)n. Надо только вспомнить, что а/b = х и (а + b)п = bn (х + 1)n. В результате получим
Формула для (a+b)4: =
=
Формула для (a+b)5: =
=
Формула бинома Ньютона позволяет обнаружить важную зависимость между биномиальными коэффициентами. Рассмотрим формулу для (x + 1)n+1 . Чему равен коэффициент при xm+1? Ясно, что это . С другой стороны (x + 1)n+1 можно получить, умножив формулу для (x + 1)n на (x + 1). Тогда (m + 1)-я степень числа х может быть получена либо при умножении слагаемого на х, либо при умножении на 1. Поэтому коэффициент в формуле для (x + 1)n+1 ' должен быть равен сумме Cnm и , т. е.
Свойства биномиальных коэффициентов
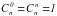
 (правило симметрии)
(правило симметрии)


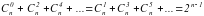
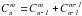 (правило Паскаля)
(правило Паскаля)
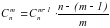
Треугольник Паскаля
Формула (*) позволяет довольно легко построить таблицу биномиальных коэффициентов, не вычисляя их по отдельности с помощью громоздкой формулы . Начнём с
того, что выпишем в одну строку бесконечное число нулей и только одну единицу среди них:
…000010000…
Ниже создадим вторую строку чисел, записывая между каждыми двумя числами первой строки их сумму. Затем под второй строкой запишем по тем же правилам третью, четвёртую и т. д.:
…0 0 0 0 1 0 0 0 0…
…0 0 0 1 1 0 0 0…
…0 0 0 1 2 1 0 0 0…
…0 0 1 3 3 1 0 0 0…
…0 0 1 4 6 4 1 0 0…
…0 1 5 10 10 5 1 0 0…
…0 1 6 15 20 15 6 1 0…
…1 7 21 35 35 21 7 1 0…
В треугольнике Паскаля п-я строка содержит биномиальные коэффициенты Сn0 ,Cn1, Cn2 ,..., Cnn Это следует из формулы (*), которая применительно к построенной таблице означает, что каждое число равно сумме двух вышестоящих.
Треугольник Паскаля обладает множеством замечательных свойств. Например, сумма чисел и-й сроки треугольника равна 2п. Чтобы доказать это, достаточно рассмотреть бином, у которого а = b= 1. С одной стороны, он равен 2n, а с другой — сумме всех биномиальных коэффициентов этой строки.
Другое свойство: количество нечётных чисел в п-й строке всегда равно степени двойки, более того, оно равно 2k , где k — число единиц в двоичной записи числа п. Например, 5-я строка содержит числа 1, 5, 10, 10, 5, 1, среди которых 4 нечётных. В то же время число 5 в двоичной системе счисления записывается как 101. Число 101 содержит 2 единицы, и 22 = 4. Ещё одно свойство треугольника Паскаля: в каждой строке сумма чисел, стоящих на нечётных местах, равна сумме чисел, стоящих па чётных местах. Чтобы убедиться в этом, рассмотрим бином, у которого а = 1, b= -1. Кроме того, если номер строки — простое число, то все числа в строке, за исключением двух крайних единиц, делятся на номер строки.
ЗАДАЧИ ПО КОМБИНАТОРИКЕ
Задача о разбиении плоскости прямыми
На сколько частей разбивают плоскость п прямых, если никакие две из них не параллельны и никакие три не проходят через одну точку?
Попробуем сначала найти ответ для небольших п. При п=1 плоскость окажется разбитой на две части (обозначим это так х1 = 2), при n= 2 — на четыре (х2 = 4). Следующее значение —x3= 7 (рис. 1). Проведём ещё одну прямую. Тут же возникает сомнение: а не будет ли число частей зависеть от расположения четвёртой прямой относительно первых трёх? В самом деле, четвёртая прямая может пересечь образованный тремя предыдущими треугольник (рис. 2), но может и обойти его (рис. 3). Число частей в обоих случаях одинаково: x4= 11. Построив пятую прямую, обнаружим, что результат опять не зависит от взаимного расположения прямых и х5 = 16. Но рисунок будет уже буквально загромождён прямыми, так что придётся ограничиться пятью первыми значениями: 2, 4, 7, 11, 16.
Обратим внимание: разности соседних чисел представляют собой последовательные натуральные числа, начиная с 2. Действительно, 4 - 2 = 2, 7 - 4 = 3, 11-7=4, 16- -11=5. Получается, что очередная, п-я по счёту прямая увеличивает число имевшихся до этого частей ровно на п. Убедимся, что так будет всегда.
Предположим, что п - 1 прямых уже есть и мы проводим ещё одну, начиная из бесконечности. Новая прямая идёт по одной из областей, на которые уже была разделена плоскость. Но вот она встретилась с какой-то прямой — и эта область разбилась надвое, т. е. появилась ещё одна часть. Прямая идёт дальше по очередной области и, встретившись со следующей прямой, разделяет надвое и эту область. Частей опять стало на одну больше. Таким образом, новая прямая пересечётся по одному разу со всеми п - 1 прямыми, и при столкновении с последней, (п - 1)-й, число частей увеличится тоже на п - 1. Но на этом прямая не обрывается: «распростившись» с последней из «старых» прямых, она режет очередную область, уходя в бесконечность.
Итак, п-я прямая действительно увеличивает число частей на п, т. е. для любого п 1 справедливо равенство хп = хn-1 + п. Остаётся найти формулу для хn в зависимости от п. Испытаем формулу вида хn = ап2 + bп + с, где а, b, с — какие-то неизвестные пока числа. Их нужно подобрать так, чтобы выполнялись два условия:
1)хn-хn-1 = п(п 1),
2)х1 = 2.
Поскольку
из первого условия получаем, что для любого п 1 должно выполняться равенство 2ап + (b -- -а) = п. Это возможно, только если 2а = 1 и b - а = 0. Значит, а =b= 1/2. Поэтому. Из второго условия следует, что х1 = = 12 /2 + 1/2 + с = 2, откуда с = 1. Окончательно
Задача о разбиении пространства плоскостями
Теперь можно рассмотреть и пространственный вариант этой задачи: требуется выяснить, на сколько частей (обозначим их уn) разбивают пространство п плоскостей, если никакие две из них не параллельны, никакие три не пересекаются по одной прямой и никакие четыре не проходят через одну точку.
Допустим, п плоскостей уже имеется и пространство разбито на yn частей. Проведём ещё одну плоскость — (п + 1)-ю. Каждая из ранее построенных плоскостей пересекается с ней по какой-либо прямой, и эти п прямых разбивают новую плоскость на хn частей. А каждая из этих частей плоскости делит некоторую ранее «отрезанную» область пространства на две части. То есть (п + 1)-я плоскость увеличивает число частей ровно на хп. Поэтому уn+1 = = уп + +хn = уn+ (п2 + п + 2) / 2. Поскольку, кроме того, y1 = 2, ясно, что данная формула позволяет вычислить уn для любого сколь угодно большого п. Можно получить и явное выражение уn через п, если по аналогии с предыдущей задачей искать уn в виде уn = an3 +bп2 + сп + d.. Приводим результат:
Обобщённый факториал и числа Каталана
На окружности заданы 2п точек. Сколькими способами их можно попарно соединить с помощью п отрезков, чтобы никакие два отрезка не пересекались?
Обозначим искомое число способов через zn. Предположив, что значения z1 , z2 , …, zn известны, найдём zn+1. Расположим на окружности 2(п + 1) точек и выберем любую из них (точка А на рис. 4). Её можно соединить с любой из остальных точек. При этом проведённая хорда разобьёт оставшиеся точки на две группы. Точки, принадлежащие разным группам, соединить нельзя — отрезок непременно пересечёт только что проведённую хорду. Значит, остается как-то соединить точки в каждой группе между собой. Но если число точек в группах нечётное, то провести отрезки не удастся — одной точке не хватит пары. Следовательно, точку A можно соединять не с каждой из прочих точек, а через одну — так, чтобы 1-й и 2-й группах оказалось соответственно О и 2п точек; 2 и 2п - 2; 4 и 2п - 4; ...; 2п и 0. Если одной из групп 0 точек, то всё многообразие соединений дают 2п точек другой группы, и иx число равно 2n. Если же в одной группе 2т ≠0 точек, а в другой 2(п - т) ≠0, то число возможных соединений становится равным 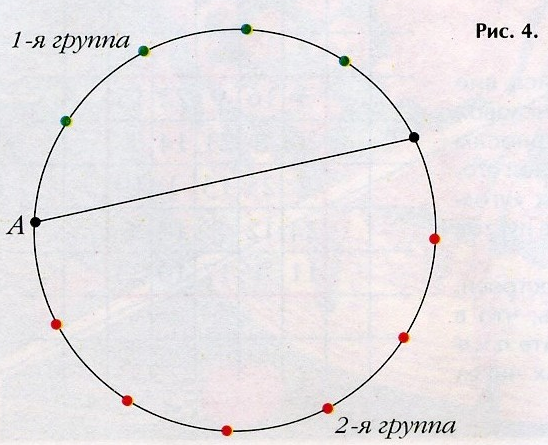
Отсюда получаем выражение для zn+1:
Используя данную формулу, можно, начиная с z1 = 1 , вычислить первые несколько значений zп :
z2=1 + 1 = 2,
z3= 2 + 1 • 1 + 2 = 5,
z4=5+ 1 • 2 + 2 • 1 + 5 = 14,
z5 = 14 + 1 • 5 + 2 • 2 + 5 • 1 + 14 = 42.
Эти числа в XVIII в. рассматривал Леонард Эйлер, правда в связи с совершенно другой за- дачей. Он подобрал (как сам признался, с большим трудом) формулу для zn:
В числителе дроби стоит так называемый обобщённый факториал.
Выражение k! означает, что перемножаются все натуральные числа подряд и наибольший из сомножителей равен k. Выражение k!! означает, что перемножаются натуральные числа через одно и наибольший сомножитель также равен k. Таким образом, если k чётное, то k!! есть произведение всех чётных чисел, не превышающих k (k!! = 2 • 4 • ... • k); если же нечётное, то это произведение всех нечётных чисел, не превышающих k (k!! = 1 • 3 •... × ×k). Аналогично, если после числа расположено три восклицательных знака, то нужно перемножать каждое третье число, а если четыре — каждое четвёртое. Применительно к нашему случаю имеем (4п - 2)!!!! = 2 • б • 10 •... • (4п - 2).
Числа zn появляются в самых разных комбинаторных задачах. Их принято называть числами Каталана в честь бельгийского математика XIX в., хотя Эйлер открыл их раньше.
ЗАКЛЮЧЕНИЕ
Комбинаторные методы находят множество применений. Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Они используются для решения транспортных задач (в частности задач по составлению расписаний), для составления планов производства и реализации продукции, в теории случайных процессов, статистике, вычислительной математике, планировании экспериментов, шахматных программах для ЭВМ и т. д. Комбинаторика используется для составления и декодирования шифров и для решения других проблем теории кодирования и теории информации. Значительную роль комбинаторные методы играют и в чисто математических вопросах — при изучении конечных геометрий, теории групп и их представлений, неассоциативных алгебр и т. д. Сочетая комбинаторные рассмотрения с изучением рентгеновских снимков, ученым удалось разгадать строение гемоглобина, инсулина и др. Торжеством комбинаторного подхода к явлениям жизни можно считать расшифровку строения дезоксирибонуклеиновой кислоты (ДНК), сделанную в Кембридже Ф. Криком и Дж. Уотсоном в 1953 г. В физике комбинаторика оказывается необходимой при изучении свойств кристаллов, описании модели ферромагнетизма и т. д. Комбинаторика оказалась полезна Дмитрию Ивановичу Менделееву в открытии периодической системы элементов . Также комбинаторика дала возможность перечислить изомеры органических соединений данного состава.
После того, как были созданы электронные вычислительные машины , роль комбинаторики возросла. Стали выходить журналы по комбинаторике, одна за другой печатаются книги, посвященные этой науке. С помощью ЭВМ стало возможно делать переборы, ранее
требовавшие сотен и тысяч лет, но возникли и новые задачи, например, как ускорить этот перебор. Возникают новые методы упаковки информации разных типов, шифрования и
дешифровки, распознавания объектов, проблемы, связанные с «электронной подписью», для анализа и успешного решения которых широко используется именно комбинаторика.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Виленкин Н.Я. и др. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. И классов с углубл. изуч. Математики / Н.Я.Виленкин., О.С.Ивашев-Мусатов, С.И.Шварцбурд. – М.: Просвещение, 1993. – 288с.
Макарычев Ю.Н. и др. Алгебра. 9 кл.: Учеб. для шк. и кл. с углубл. изуч. математики. – М.: Мнемозина, 2004. – 439с.
Макарычев Ю.Н., Миндюк Н.Г. Алгебра: Элементы статистики и теории вероятностей: Учеб. пособие для учащихся 7-9 кл. общеобразоват. учреждений / Под. ред. С.А.Теляковского. – М.: Просвещение, 2003. – 78с.
Мордкович А.Г., Семенов П.В. События. Вероятности. Статистическая обработка данных: Доп. параграфы к курсу алгебры 7-9 кл. общеобразоват. учреждений. – М.: Мнемозина, 2004. – 112с.
Решение задач по статистике, комбинаторике и теории вероятностей. 7-9 классы / Авт.-сост. В.Н.Студенецкая. – Волгоград: Учитель, 2005. – 429с.
Ткачева М.В., Федорова Н.Е. Элементы статистики и вероятность: Учеб. пособие для 7-9 кл. общеобразоват. учреждений. – М.: Просвещение, 2004. – 112с.
www.bymath.net/studyguide/alg/sec/alg31.html
www.math4you.ru/theory/TerVerMatStat/TerVerKom/
www.pm298.ru›Формула Ньютона
19
Похожие файлы
object(ArrayObject)#862 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(91) "Работа с одаренными детьми для начальных классов "
["seo_title"] => string(53) "rabota-s-odariennymi-diet-mi-dlia-nachal-nykh-klassov"
["file_id"] => string(6) "233607"
["category_seo"] => string(16) "nachalniyeKlassi"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1443164465"
}
}
object(ArrayObject)#884 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(87) "Проектная деятельность по теме "Комбинаторика" "
["seo_title"] => string(50) "proiektnaia-dieiatiel-nost-po-tiemie-kombinatorika"
["file_id"] => string(6) "223426"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(5) "uroki"
["date"] => string(10) "1437662410"
}
}
object(ArrayObject)#862 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(149) "Программа спецкурса по математике «Решение задач повышенной сложности» (7 класс) "
["seo_title"] => string(89) "proghramma-spietskursa-po-matiematikie-rieshieniie-zadach-povyshiennoi-slozhnosti-7-klass"
["file_id"] => string(6) "236084"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1443957822"
}
}
object(ArrayObject)#884 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(102) "Элективный курс "Железнодорожный транспорт в проектах" "
["seo_title"] => string(59) "eliektivnyi-kurs-zhielieznodorozhnyi-transport-v-proiektakh"
["file_id"] => string(6) "107243"
["category_seo"] => string(11) "informatika"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1403190007"
}
}
object(ArrayObject)#862 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(117) "Внеурочная деятельность. Программа кружка "Весёлая математика" "
["seo_title"] => string(70) "vnieurochnaia-dieiatiel-nost-proghramma-kruzhka-viesiolaia-matiematika"
["file_id"] => string(6) "173198"
["category_seo"] => string(10) "vneurochka"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1423936079"
}
}
Подтверждение авторства
Пожалуйста, введите ваш Email.
Если вы хотите увидеть все свои работы, то вам необходимо войти или зарегистрироваться
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт















