Муниципальное автономное общеобразовательное учреждение
«Средняя общеобразовательная школа № 28» г.Сыктывкара
Проектная работа
«Математика и культура»
Выполнила: Размыслова Анна,
3б класс,
Руководитель: Иванова Ю.А.
Сыктывкар, 2014
Содержание
Введение 3
1. Математика и архитектура 4
2.Математика и живопись 7
3. Математика и музыка 9
Заключение. 12
Список литературы 13
Введение
Многие люди не замечают связи математики и культуры, и не считают ее значимой.
Поэтому было принято решение продемонстрировать на примерах ошибочность мнения о скучности математики и ее законов, о малой практической применимости в культуре законов математики и ее свойств. Показать, что без математики не обойтись.
Чтобы показать данную связь, мы рассмотрели три составляющих культуры: архитектуру, живопись и музыку.
Цель работы – показать взаимосвязь математики и культуры.
Задачи работы:
рассмотреть связь между математикой и архитектурой.
выявить, чем связаны математика с живописью.
проанализировать связь математики с музыкой.
сделать выводы.
Методы исследования:
изучение и анализ литературы по данной теме;
подбор фактов, подтверждающих связь математики с культурой;
сбор информации.
Математика и архитектура
Понятие «архитектура» имеет несколько смыслов. Архитектура – древнейшая сфера человеческой деятельности и зарождается вместе с человечеством, сопровождает его в историческом развитии. В ней отражаются мировоззрение, ценности, знания людей, живших в различные исторические эпохи. Архитектурные памятники, дошедшие до нас из глубины веков, помогают нам понять цели, взгляды, мысли, традиции и привычки, представления о красоте, уровень знаний людей, которые когда-то жили на Земле.
Архитектурные сооружения возводились для удобства жизни и деятельности человека. Они должны были служить его пользе: беречь его от холода и жары, дождей и палящего солнца. Возводимые сооружения должны быть прочными, безопасными и долго служить людям. Но человеку свойственно еще и стремление к красоте, поэтому все, что он делает, он старается сделать красивым.
В архитектуре тесно переплетены и строго уравновешены наука, техника и искусство. Математические фигуры послужили архитектуре и возвели исторические объекты в разных сранах мира.
Как же математика может помочь в планировании архитектурного объекта?
Математика принимает непосредственное участие в обеспечении прочности и пользы архитектурных сооружений.
Люди с древних времен, возводя свои жилища, думали, в первую очередь, об их прочности. Прочность связана и с долговечностью. На возведение зданий люди тратили огромные усилия, а значит, были заинтересованы в том, чтобы они простояли как можно дольше. Кстати, благодаря этому, до наших дней дошли и древнегреческий Парфенон, и древнеримский Колизей.
Прочность сооружения обеспечивается не только материалом, из которого оно создано, но и конструкцией, которая используется в качестве основы при его проектировании и строительстве. Прочность архитектурных сооружений, важнейшее их качество. Связывая прочность, во-первых, с теми материалами, из которых они созданы, а, во-вторых, с особенностями конструктивных решений, оказывается, прочность сооружения напрямую связана с той геометрической формой, которая является для него базовой.
Другими словами, речь идет о той геометрической фигуре, которая может рассматриваться как модель соответствующей архитектурной формы. Оказывается, что геометрическая форма также определяет прочность архитектурного сооружения.
Самым прочным архитектурным сооружением с давних времен считаются египетские пирамиды. Как известно они имеют форму правильных четырехугольных пирамид.
Именно эта геометрическая форма обеспечивает наибольшую устойчивость за счет большой площади основания. С другой стороны, форма пирамиды обеспечивает уменьшение массы по мере увеличения высоты над землей. Именно эти два свойства делают пирамиду устойчивой, а значит и прочной в условиях земного тяготения.
«Рациональность» геометрической формы пирамиды, которая позволяет выбирать и внушительные размеры для этого сооружения, придает пирамиде величие, вызывает ощущение вечности и внушительности.
На смену пирамидам пришла стоечно-балочная система. С точки зрения геометрии она представляет собой многогранник, который получится, если мысленно на два вертикально стоящих прямоугольных параллелепипеда поставить еще один прямоугольный параллелепипед.
Это одна из первых конструкций, которая стала использоваться при возведении зданий и представляет собой сооружения, которые состоят из вертикальных стоек и покрывающих их горизонтальных балок. Первым таким сооружением было культовое сооружение – дольмен. Оно состояло из двух вертикально поставленных камней, на которые был поставлен третий вертикальный камень. Назначение этого культового сооружения до сих пор неясно. Однако в нем воплощена идея преодоления человеком силы притяжения.
Кроме дольмена, до нас дошло еще одно сооружение, представляющее простейшую стоечно-балочную конструкцию – кромлех. Это также культовое сооружение, предположительно предназначенное для жертвоприношений и ритуальных торжеств. Кромлех состоял из отдельно стоящих камней, которые накрывались горизонтальными камнями. При этом они образовывали две или несколько концентрических окружностей.
Самый знаменитый кромлех сохранился до наших дней в местечке Стоунхендж в Англии. Некоторые ученые считают, что он был древней астрономической обсерваторией. Сегодня это сооружение связывают с посещением Земли инопланетянами.
До сих пор стоечно-балочная конструкция является наиболее распространенной в строительстве. Большинство современных жилых домов в своей основе имеют именно стоечно-балочную конструкцию.
Камень, из которого возводились сооружения на основе стоечно-балочной конструкции, плохо гнется, он обычно разрушается под действием своего собственного веса. Поэтому под балки нужно было ставить достаточно много стоек. Их делали в виде колонн различного вида. Для того чтобы украсить здание такие колонны облачали в формы кариатид или атлантов.
Камень плохо работает на изгиб, но хорошо работает на сжатие. Это привело к использованию в архитектуре арок и сводов. Так возникла новая арочно-сводчатая конструкция.
С появлением арочно-сводчатой конструкции в архитектуру прямых линий и плоскостей, вошли окружности, круги, сферы и круговые цилиндры. Первоначально в архитектуре использовались только полуциркульные арки или полусферические купола. Это означает, что граница арки представляла собой полуокружность, а купол – половину сферы. Например, именно полусферический купол имеет Пантеон – храм всех богов - в Риме. Диаметр купола составляет 43 м. При этом высота стен Пантеона равна радиусу полусферы купола. В связи с этим получается, что само здание этого храма как бы «накинуто» на шар диаметром 43 м.
Этот вид конструкции был наиболее популярен в древнеримской архитектуре. Арочно-сводчатая конструкция позволяла древнеримским архитекторам возводить гигантские сооружения из камня. К ним относится знаменитый Колизей или амфитеатр Флавиев. Свое название он получил от латинского слова colosseus, которое переводится как колоссальный, или огромный.
Эта же конструкция использовалась при создании гигантских терм (бань) Каракаллы и Диоклетиана, вмещавших одновременно до 3 тысяч посетителей. Сюда же следует отнести и систему арочных водоводов-акведуков, общая протяженность которых составляла 60 км.
Всем была хороша арочно-сводчатая конструкция, но она имела один недостаток – слишком большая сила действовала в основании арок (сводов) наклонно вбок (в отличие от стоечно-балочной конструкции, где сила тяжести действует вертикально). Эти боковые усилия, которые архитекторы называют боковым распором, требуют большой толщины стен, которая должна гасить эти усилия. Так, например, толщина стен Пантеона в Риме, поддерживающих купол, равна 7 метрам. Это требовало большого расхода материалов.
Следующим этапом развития архитектурных конструкций явилась каркасная система, которая в основном используется в современной архитектуре. Прообразом ее стала разновидность арочно-сводчатой конструкции, содержащей стрельчатые арки.
Арочная конструкция послужила прототипом каркасной конструкции, которая сегодня используется в качестве основной при возведении современных сооружений из металла, стекла и бетона. Достаточно вспомнить конструкции известных башен: Эйфелевой башни в Париже и телебашни на Шаболовке.
Архитектурные произведения живут в пространстве, являются его частью, вписываясь в определенные геометрические формы. Кроме того, они состоят из отдельных деталей, каждая из которых также строится на базе определенного геометрического тела. Часто геометрические формы являются комбинациями различных геометрических тел.
Геометрическая форма сооружения настолько важна, что бывают случаи, когда в имени или названии здания закрепляются названия геометрических фигур. Так, здание военного ведомства США носит название Пентагон, что означает пятиугольник. Связано это с тем, что, если посмотреть на это здание с большой высоты, то оно действительно будет иметь вид пятиугольника. На самом деле только контуры этого здания представляют пятиугольник. Само же оно имеет форму многогранника.
Но чаще всего в архитектурном сооружении сочетаются различные геометрические фигуры. Например, в Спасской башне Московского кремля в основании можно увидеть прямой параллелепипед, переходящий в средней части в фигуру, приближающуюся к цилиндру, завершается же она пирамидой. Конечно, можно говорить о соответствии архитектурных форм указанным геометрическим только приближенно, отвлекаясь от мелких деталей. При более детальном рассмотрении и изучении деталей можно увидеть: круги – циферблаты курантов; шар – основание для крепления рубиновой звезды; полукруги – арки одного из рядов бойниц на фасаде башни и т.д.
Таким образом, можно говорить о пространственных геометрических фигурах, которые служат основой сооружения в целом или отдельных его частей, а также плоских фигурах, которые обнаруживаются на фасадах зданий.
Нужно сказать, что у архитекторов есть излюбленные детали, которые являются основными составляющими многих сооружений. Они имеют обычно определенную геометрическую форму. Например, колонны это цилиндры, купола – полусфера или просто часть сферы, ограниченная плоскостью, шпили – либо пирамиды, либо конусы.
Фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза. А это соотношение в математике принято считать «золотой пропорцией».
Золотое соотношение мы можем увидеть и в пирамиде Хеопса, и в здании собора Парижской Богоматери, и в храме Василия Блаженного на Красной площади.
Симметрия – царица архитектурного совершенства. Соблюдение симметрии является первым правилом архитектора при проектировании любого сооружения. Стоит только посмотреть на великолепное произведение А.Н.Воронихина Казанский собор в Санкт-Петербурге, чтобы убедиться в этом. Если мы мысленно проведем вертикальную линию через шпиль на куполе и вершину фронтона, то увидит, что с двух сторон от нее абсолютно одинаковые части сооружения (колоннады и здания собора).
Математика и архитектура шагают нога в ногу, помогая друг другу, по дороге к новым инновациям.
Математика и живопись
«Математика в живописи? Ну, это уж слишком! — скажете вы. — Архитектура, да — это наполовину наука, наполовину искусство, и потому «математическое начало» в ней естественно. Но какая математика нужна художнику, которому кроме холста и красок вообще ничего не нужно?!»
Именно в живописи заключены основные математические проблемы изобразительного искусства. Что же это за проблемы?
Ещё в эпоху Возрождения художники открыли, что любая картина имеет определённые точки, невольно приковывающие внимание, так называемые зрительные центры. При изображении объектов на картине важно правильно их расположить. На первый взгляд было бы расположить объект по середине, но это не так. Наиболее гармоничными смотрятся объекты, расположенными согласно золотому сечению. Таких точек всего 4, они делят величину изображения по горизонтали и вертикали в золотом сечении. Часто используются четыре точки, расположенные на расстоянии 3/8 и 5/8 от соответствующих краёв плоскости. Данное открытие у художников того времени получило название «Золотое сечение» картины.
Переходя к примерам в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.
Портрет Моны Лизы привлекает нас тем, что композиция рисунка построена на «золотых треугольниках».
На этой замечательной картине И. И. Шишкина («Сосновая роща») так же просматриваются мотивы золотого сечения.
Примером использования данного приёма является картина «Утро в сосновом лесу».
Наличие в картине вертикалей и горизонталей, делящих её в отношении золотого сечения, придаёт ей характер уравновешенности и спокойствия.
Золотое сечение можно встретить в бытовых предметах и шрифтах.
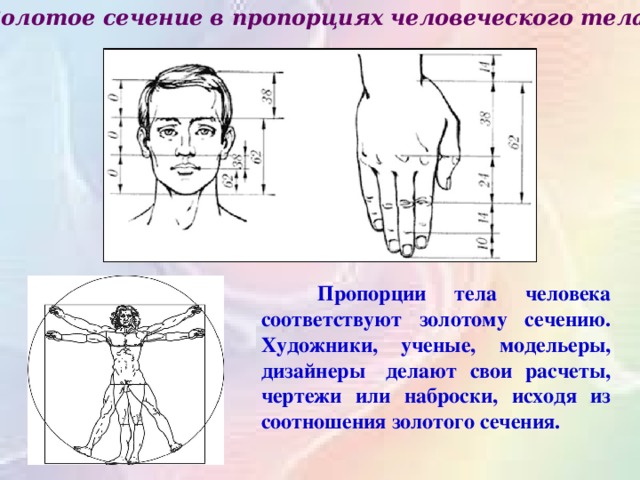
Золотое сечение в пропорциях человеческого тела.
Пропорции тела человека соответствуют золотому сечению. Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Они используют мерки с тела человека, сотворенного также по принципу золотой сечения. Леонардо Да Винчи и Ле Корбюзье перед тем как создавать свои шедевры брали параметры человеческого тела, созданного по закону Золотой пропорции.
Фракталы
Фрактал - термин, означающий сложную геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.
Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения.
Также фракталы применяются в моделирование, с помощью них можно создать компьютерные модели, имеющие шероховатые поверхности и которые при увеличении не будут иметь плоские поверхности
Но фракталы это ещё и очень красиво, с помощью них можно создавать фигуры, поразительной красоты.
Золотая спираль
При зрительном восприятии на картине предметов, изображенных на основе использования золотого сечения, ощущаются гармония, покой, соразмерность, стройность.
Напротив, ощущение динамики, волнения проявляется сильней всего в другой простейшей геометрической фигуре – спирали. Спираль – это плоская линия, образованная движущейся точкой, которая удаляется по определенному закону от начала луча, равномерно вращающегося вокруг своего начала. Если точка удаляется от начала равномерно (r=kj, где r – расстояние от начала, а j - угол поворота луча), то получается спираль Архимеда
Многофигурная композиция, выполненная в 1509-1510 Рафаэлем, когда прославленный живописец создал свои фрески в Ватикане, как раз отличается динамизмом и драматизмом сюжета. Рафаэль так и не довел свой замысел до завершения, однако, его эскиз был гравирован известным итальянским графиком Маркантонио Раймонди, который на основе этого эскиза и создал гравюру «Избиение младенцев»
Симметрия Симметрия (соразмерность, одинаковость в расположении частей какого-либо рисунка относительно точки, прямой, плоскости) – это понятие не только чисто математическое. Она есть и в творениях природы (животные, листья растений, кристаллы), и в творениях конструкторов, архитекторов, скульпторов, художников (рис. 14) и т. д.
Для анализа симметрии изображения лучше взять картину с более простой композицией. Можно обратиться к хранящейся в Эрмитаже картине гениального итальянского художника и ученого Леонардо да Винчи «Мадонна Литта»
Геометрические формы С середины XIX века отход от господствующей в это время в изобразительном искусстве натуралистической традиции резко ускоряется. Живопись, графика, скульптура обращаются к тому, что не доступно прямому («буквальному») восприятию.
Последняя выставка импрессионистов в 1886г. знаменует конец классического периода европейского искусства. Начиная с этого времени, в европейской живописи одно за другим возникают многочисленные течения: югендстиль, экспрессионизм, неоимпрессионизм, пуантилизм, символизм, кубизм, фовизм.
Кубизм – авангардское течение в изобразительном искусстве I-й четверти XX в. Геометрическая красота фигур – именно то, что прежде всего бросается в глаза в этой картине
Одним из видов абстракционизма является геометрическая абстракция, в основе которой лежит композиция геометрических или стереометрических фигур.
Математика и музыка
Математика — самая абстрактная из наук, а музыка — наиболее отвлеченное из искусств, это высшие выразители науки и искусства.
Первые попытки математического осмысления искусства, так же как и сами истоки математики и искусства, теряются в глубине веков задолго до нашей эры. Но это были скорее случайные совпадения, чем глубокомысленный расчёт. А вот осмысленное и систематическое приложение к искусству математика нашла, конечно, в музыке, в трудах древнегреческого математика Пифагора и Аль-Фараби. Какая связь может быть между математикой, мудрой царицей всех наук, и музыкой? Как могут взаимодействовать такие совершенно разные человеческие культуры?
В музыке все считать надо. Как и в математике.
7 нот, 5 линеек нотного стана, интервалы.
А ноты-то все разные. Одни коротенькие совсем, другие длинные.
Так в 5-6 лет ребята, которые занимаются музыкой, узнают, что ноты или что-нибудь другое может делиться. А деление школьники начинают изучать только в 8-9 лет, в конце второго класса. Интересно, что у истоков музыкальной грамотности стоял великий математик Пифагор. И не случайно!
Чтобы записать слова – мы используем буквы, числа – цифры, а музыку – ноты.
При записи мелодии, звуки имеют свою длину (длительность).
Здесь и происходит сопоставление целого числа и целой длительности, дробного числа и длительности коротких нот, записываемых при помощи дроби.
Ноты:
Целые ноты.
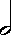Половинки – 1/2.
Четверти – 1/4.
Восьмые – 1/8.
Не зная математических понятий, не умея различать дроби, не умея сравнивать их, невозможно было бы сыграть музыкальный фрагмент.
Именно здесь мы сталкиваемся с математической операцией сравнения.
В музыке, как и в математике, тоже есть понятие параллельности. Параллельные тональности, а ещё линии нотного стана всегда параллельны, то есть никогда не пересекаются.
Кроме вышеупомянутых понятий, с понятием последовательность в математике мы встречаемся крайне часто. Обычно цель при встрече с ними – отгадать следующее число или символ.
Все музыкальные произведения тоже записываются нотами в определенной музыкальной последовательности.
Таким образом, математика и музыка – два полюса человеческой культуры, два школьных предмета, две системы мышления, тесно связанные между собой:
Музыкальные и математические операции родственны и содержательно и психологически.
Занимаясь музыкой, человек развивает и тренирует свои математические способности.
Симметрия в музыке.
Симметрия часто используется в музыке. Ряд музыкальных форм строится симметрично. В этом отношении особо характерно рондо (рондо от фр. – круг).
«Душа музыки - ритм, он состоит в правильном периодическом повторении частей музыкального произведения», - писал в 1908 г.известный русский физик Г. В. Вульф, - « Правильное же повторение – сущность симметрии».
Приложим к музыкальному произведению понятие симметрии при помощи нот, т. е. получаем пространственный геометрический образ.
Ритмы.
Слово «ритм» изначально принадлежало музыке, хотя сегодня неудивительно, что оно может быть известно человеку совершенно из других источников. Даже в словаре Ожегова «ритм» определяется как равномерное чередование каких-нибудь элементов. Музыкальный ритм дается как пример, а не как определение. Таким образом, «ритм» можно назвать общим понятием в области науки и искусства.
Математика также заимствовала данное слово. Исследуя математические закономерности и числовые последовательности, часто можно обнаружить ритмичность. В частности, «простейшими» примерами математических ритмов являются периодические дроби (кстати, слово «период» также знакомо музыкантам).
Прогрессия.Арифметическая прогрессия – числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.
Геометрическая прогрессия – числовая последовательность, первый член которой отличен от нуля, а каждый последующий равен предыдущему, умноженному на одно и то же число.
Как ни странно, обе эти прогрессии «живут» и в музыке.
Интересно, что принцип построения длительностей соответствует принципу построения геометрической прогрессии. И если записать длительности от «целой» (которая принята в музыке за единицу) по степени убывания, то получим:
В математике такая последовательность называется бесконечно убывающей геометрической прогрессией, как бесконечная геометрическая прогрессия, модуль знаменателя которой меньше единицы (в данном случае – 
).
Понятие арифметической прогрессии. Связано с музыкальным понятием квинтовый круг.
Таким образом, можно сделать вывод, что в музыке все считать надо. Как и в математике. Не зная математических понятий, не умея различать дроби, не умея сравнивать их, невозможно было бы сыграть музыкальный фрагмент.
В музыке, как и в математике, тоже есть понятие параллельности. Параллельные тональности, а ещё линии нотного стана всегда параллельны, то есть никогда не пересекаются. Музыкальные и математические операции родственны и содержательно и психологически. Занимаясь музыкой, человек развивает и тренирует свои математические способности.
Заключение.
Для многих мир математики – это только задачи, формулы, перпендикуляры, треугольники…. Но для некоторых этот мир кажется красочным, ярким, удивительным и загадочным, поэтому им удалось самим удивить мир людей и их имена вошли в историю, хотя не все их понимали.
В ходе выполнения работы, мы узнали много интересных фактов, при постройке, как современных зданий, так и зданий прошлых веков необходимы знания математики. Архитектурное формообразование с помощью геометрических построений сохраняется во всех случаях. Эта проблема стояла перед архитекторами прошлых веков, не исчезла она и сегодня.
В XXI веке геометрия и архитектура превратила наши города в величественные мегаполисы. В современном мире все здания и сооружения имеют различные геометрические формы. Большинство из них это многогранники.
Музыка помогает изучать математику. Ребятам, которые занимаются музыкой легче справляться с математикой в школе. Математика, как наука может развиваться без музыки, а музыкальное искусство подчиняется многим законам математики и не может существовать без неё.
Живопись формируется, основываясь на расчетах, используя геометрические законы, применяя математические методы, компьютерную графику. Художники, и дизайнеры с помощью математики создают для нас такие произведения искусств, которые улучшают эмоциональное состояние человека, повышают его работоспособность.
Примеры взаимопроникновения математики в различные сферы культуры и искусства и наоборот можно приводить бесконечно… И чем дальше этим занимаешься, тем увлекательнее становится такая работа. Но даже приведенных примеров, достаточно для того, чтобы согласиться со словами с тем, что культурой называют совокупность всех материальных и духовных ценностей, накопленных человечеством за определенную историческую эпоху. И какой бы исторический отрезок мы ни взяли, какими бы географическими рамками ни ограничились, там всегда присутствует математика.
Список литературы
Волошинов А.В. Математика и искусство. М.: Просвещение. 2000.
Самойлик Г. Леонардо да Винчи. // Математика. Приложение к газете «Первое сентября». – М., 2003. – № 4. – С. 7-10.
Ятайкина А., Пашкина О. О золотом сечении и не только о нем. // Математика в школе. Научно-теоретический и методический журнал МО РФ. – М.: «Школьная пресса», 2001. – № 3. – С. 75-76.
Я познаю мир: Детская энциклопедия.Архитектура.1990
www.abc-people.com/data/leonardov/zolot_sech-txt.htm - «Золотое сечение».
http://letopisi.org/index.php/Проект_Музыкальная_математика - Проект «Музыкальная математика».
http://virartech.ru/articles/musical_mathematics.php - А. Устинов «Музыка и математика».
http://www.pandia.ru/text/77/21/70809.php - Энциклопедия знаний. Математика и архитектура.
13
