Проект "Теорема Пифагора"

1. Ознакомление учащихся с историей развития теоремы Пифагора и фактами из жизни Пифагора;

2. Ознакомление со способами доказательства теоремы;

3. Развитие навыков решения задач с помощью теоремы Пифагора.

Развивающие цели:

1.Развитие познавательного интереса учащихся;

2.Развитие умение работать с информационными ресурсами;

3. Развитие самостоятельности в подборе материала по теме.

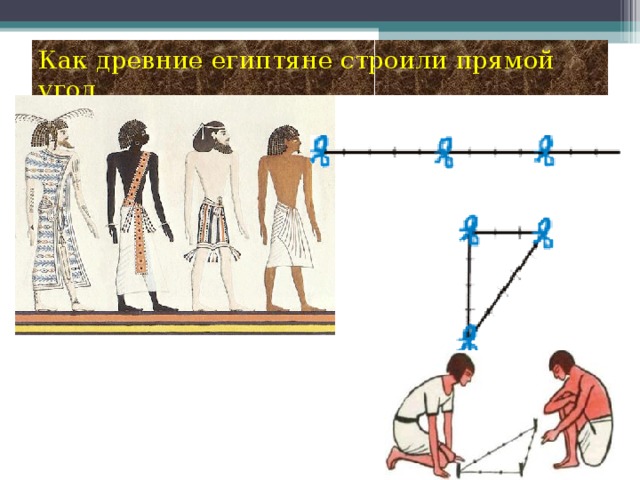
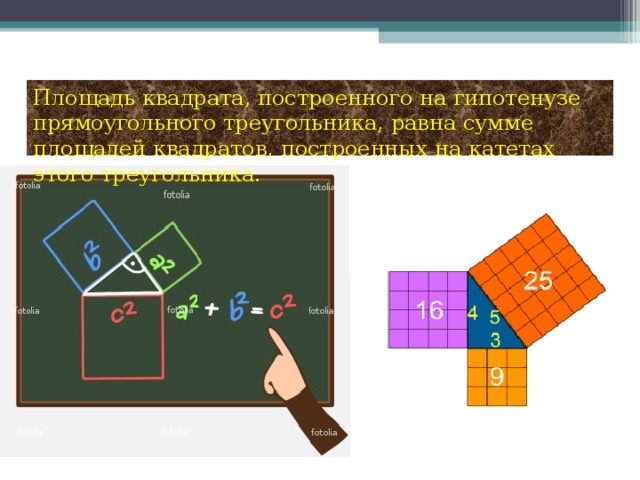
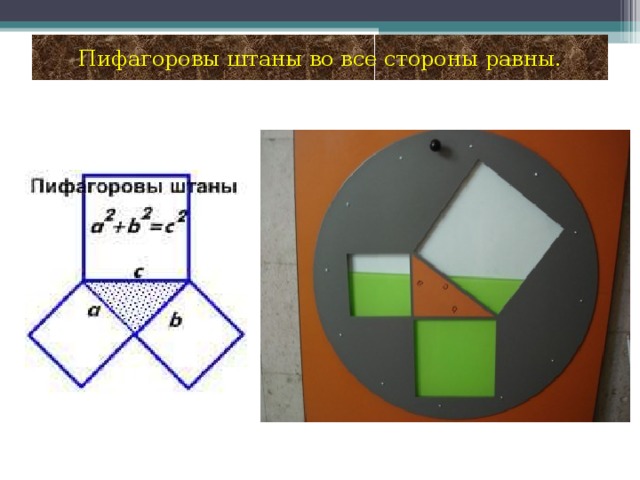
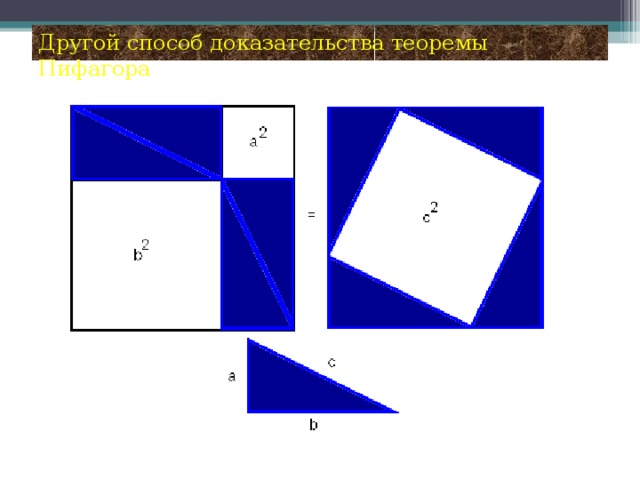
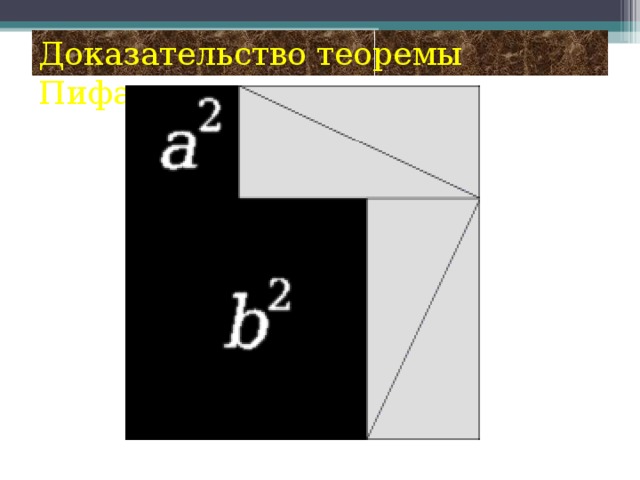
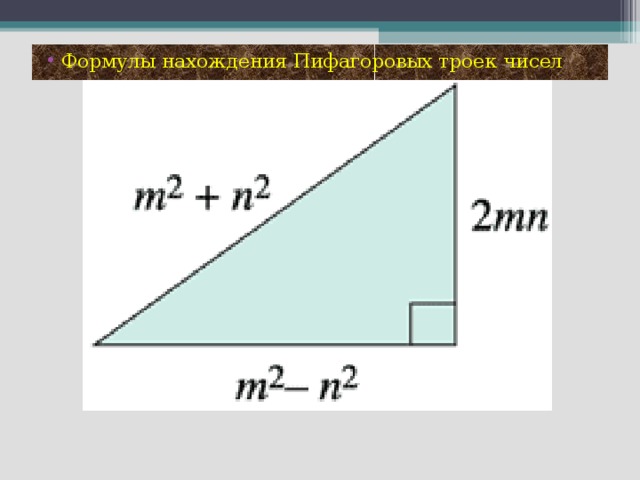
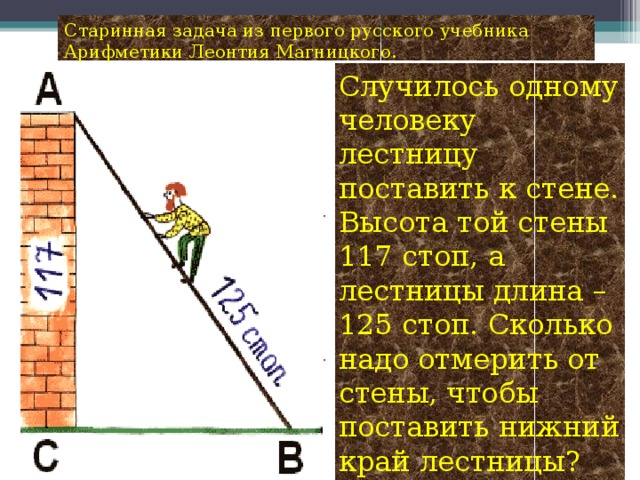
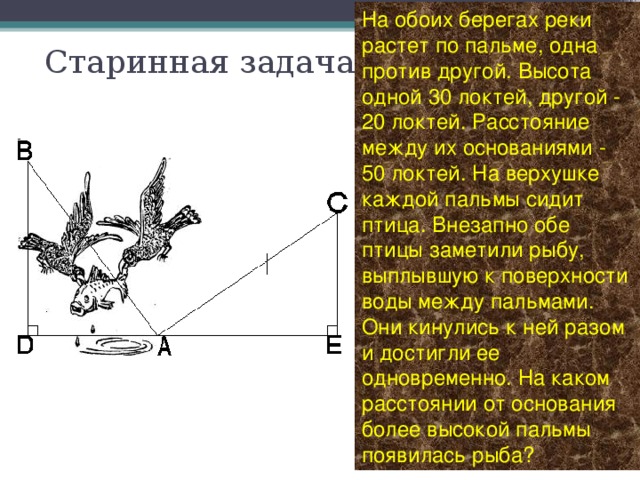
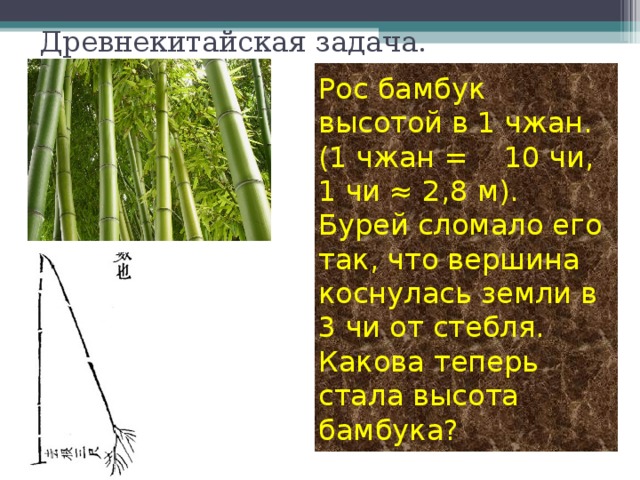
План проведения проекта:

1 этап: Постановка основополагающего и проблемных вопросов

2 этап: Ознакомление с основными этапами жизни и деятельности Пифагора

3 этап: Формулировка и доказательство теоремы Пифагора

4 этап: Способы доказательства теоремы.

5 этап: Использование теоремы Пифагора в жизни.

6 этап: Защита проекта.

Группа «Историки»

Наш проект называется «Теорема Пифагора». Это одна из основных теорем геометрии о свойствах сторон прямоугольного треугольника, поэтому Нина Петровна заранее дала нам задание, узнать, как строили прямой угол в древнем Египте, кто такой Пифагор, каковы его заслуги перед человечеством, почему эта теорема названа его именем, как он её доказал.

Вот что мы узнали в процессе работы над этим проектом.

Пифагор – древнегреческий математик, философ, религиозный и политический деятель. Он родился на острове Самос. Пифагор – это не имя, а прозвище, означающее «Убеждающий речью». С юных лет он стремился проникнуть в тайны великой природы. Первое образование он получил в храмах древней Греции. Но этих знаний ему было недостаточно. В возрасте 18 лет он отправился в поисках мудрости в Египет, где прожил 22года.

С группой пленников Пифагор попал из Египта в Вавилон, где продолжал своё образование ещё 12 лет. Приблизительно в 530 году до нашей эры он возвращается в Грецию, а затем переселяется в Южную Италию, в город Кротон. Там он прожил более 25 лет.

В Кротоне он основал пифагорейский союз, который одновременно был философской школой, политической партией и религиозным братством.

Обучение в школе продолжалось пятнадцать лет. Первые пять лет ученик должен был молчать: это приучало его к сосредоточенности. Вторые пять лет ученики могли только слушать речи учителя. Только последние пять лет ученики могли беседовать с учителем лицом к лицу.

Пифагорейская система знаний состояла из четырёх разделов:

1. Арифметика, наука о числах. 2.Геометрия, учение о фигурах. 3. Музыка.

4. Астрономия.

По утрам пифагорейцы молились и пели гимн восходящему солнцу. Школа Пифагора дала Греции много талантливых математиков, физиков и философов.

Главным пифагорейским символом здоровья и опознавательным знаком была пентаграмма или пифагорейская звезда. Пифагорейцы называли эту фигуру самой совершенной и считали, что она уберегает от нечистой силы. Пятиконечной звезде около 3000 лет, но и сегодня она реет на флагах очень многих государств.

Мы попробовали создать свои варианты пифагорейской звезды.

Пифагор впервые ввёл термин «Философ». Когда его спросили, кем он является, он ответил: «Я не мудрец, я любитель мудрости, то есть философ». До наших дней дошли афоризмы Пифагора, которые многому учат. Некоторые из них мы вывесили во время недели математики. Известен афоризм Пифагора «Пьянство – упражнение в безумии». В истории осталась любопытная придумка Пифагора – кружка жадности. Когда её наполняют до определённого уровня, то она такой и остаётся, но когда её переполняют, то всё содержимое вытекает, что объясняется гидростатическим давлением. Она и сейчас пользуется в Греции большим спросом как сувенир.

Наставления Пифагора всегда начинались словами: «Самое мудрое на свете – число, числа правят миром». До сих пор сохранились значения чисел по Пифагору. Именно Пифагор стал основателем мистического учения о числах. От Пифагора и его последователей и пошли всякие суеверия, связанные с числами.

Группа «Исследователи»

И всё-таки, самое главное, что досталось нам от Пифагора, это теорема, названная его именем: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Это свойство треугольника было известно и до Пифагора.

Уже древние египтяне знали, что если построить треугольник со сторонами 3, 4, 5, то один из углов будет прямым. Но они пришли к этому практическим путём, а доказать не могли. У них было такое правило: «Делай, как делается».

Мы так же, как египтяне, строили прямоугольный треугольник с помощью шнура, разделённого на 12 равных частей.

Так в чём же заслуга Пифагора, если задолго до него египтяне знали, что треугольник со сторонами 3, 4, 5 – прямоугольный? Пифагор доказал, что это свойство верно для любого прямоугольного треугольника. А произошло это так. К Пифагору пришли землемеры и попросили помочь им построить квадрат, площадь которого будет ровно в 2 раза больше площади первого квадрата. В результате неоднократных вычислений Пифагор пришёл к выводу, что если на гипотенузе равнобедренного треугольника построить квадрат, то его площадь будет равна сумме площадей квадратов, построенных на катетах. То есть, площадь большего квадрата в 2 раза больше площади малого квадрата. Так у него получился чертёж, который ученики до сих пор в шутку называют «Пифагоровы штаны во все стороны равны». А уже затем Пифагор доказал, что это свойство верно для любого прямоугольного треугольника.

Нам понравилось вот такое наглядное доказательство этой теоремы: Если на сторонах прямоугольного треугольника построить сообщающиеся сосуды и наполнить их водой, то легко убедиться, что ёмкость большего сосуда равна сумме ёмкостей двух меньших сосудов.

А вот ещё одно наглядное доказательство: Построим два равных квадрата со стороной (a+b) и разрежем их так, как показано на рисунке. Если от каждого квадрата отрезать по 4 равных треугольника, то видно, что от первого квадрата остаются два квадрата, в сумме равные остатку от второго квадрата. Вот ещё одно доказательство с анимацией.

Теорему Пифагора называют теоремой-рекордсменкой, потому что существует более 100 различных способов её доказательства. Это единственная теорема, в честь которой даже была выпущена почтовая марка.

Заслуга Пифагора и в том, что он вывел формулы, по которым легко найти тройку таких чисел, что с²=а²+в²

Группа «Практики».

Нужно взять два взаимно простых числа m n и с помощью формул найти гипотенузу и катеты. Каждый из нас также нашёл свою тройку Пифагоровых чисел.

На уроках мы решали задачи с помощью теоремы Пифагора. Причём, не только из учебника, но и старинные задачи, которые мы нашли в интернете и сделали к ним рисунки и чертежи.

Задачи из учебника арифметики Магницкого, древнекитайская задача, древнеегипетская.

Теперь мы знаем, что

Если дан нам треугольник, и притом с прямым углом,

То квадрат гипотенузы мы всегда легко найдём:

Катеты в квадрат возводим, сумму степеней находим,

И таким простым путём к результату мы придём.

Спасибо за внимание!