ПРАКТИЧЕСКАЯ РАБОТА
«Производная»
Учитель математики
Нагаева С.Н.
МАОУ «Лицей №1»
г. Березники
Пермский край
г. Березники, 2014 г.
ПРАКТИЧЕСКАЯ РАБОТА
«Система заданий по отработке учебных элементов:
1) умение находить производную функции, используя таблицу производных элементарных функций и правила нахождения производных;
2) умение вычислять значение производной в точке;
3) владение геометрическим смыслом производной».
I. Умение находить производную функции
1) Базовый уровень сложности задания
Найдите производную функции:
а) y = (4-3х)5 y' = -15(4-3х)4
б) y = ех + 6х2 y' = ех + 12х
в) y = + 3sin x – y' =
г) y = cos2 x y' = - sin2x
д) y = x6 y' = x5 (6+1)
2) Повышенный уровень сложности задания
a) y= 3e2x - y' = 6e2x -
б) y = sin4x+cos5x+2x3 y'=4 sin3x cos x-5sin5x+6x2
в) y = y' =
г) y = y' = -
д) y = y' = -
II. Умение вычислять значение производной в точке.
1) Базовый уровень сложности задания.
Найдите значение производной данной функции в точке хо:
а) y = (4-3x)6; xo = 1 (y' = -18(4-3x)5; -18)
б) y = x xo=2 (2+1)
в) y = xsin (3x- xo= (
2) Повышенный уровень сложности задания
а) y = xo = -2 (
б) y = xo = -1 (-
в) Найдите значения а и в, при которых выполняются данные условия:
y=a sin4x+в cos2x; y' (y' ( (a=
г) y = a sin2x + в cos x; y' ( y' ( (a=o; в = -4).
3) Высокий уровень сложности задания.
Для функции y = найдите производную в точке
хо = (-
III. Владение геометрическим смыслом производной.
1)Базовый уровень.
Напишите уравнение касательной к графику функции ƒ в точке с абсциссой хо:
а) ƒ х)= х3 – 3х2; хо= -1 y = 9x+5
б) ƒ(х) =-х3 + х – 1; хо =-2 y = -11x-17
в) ƒ(х) = 2х2-5х+1; хо = 2 y = 3x-7
г) ƒ(х) = 3х2 – 4х – 2; хо = -1 y = -10x-5
2) Повышенный уровень.
Напишите уравнение касательной к графику функции ƒ в точке с ординатой yo:
а) ƒ(х) = yo = 32 y = -2x + 34
б) ƒ(х) = yo = 8 y = 4x+4
в) При каком значении а данная прямая является касательной к графику функции ƒ
y = a x-5; ƒ(x)=3x2-4x-2. (a = -10; a = 2)
3) Высокий уровень
Составьте уравнение касательной к графику функции ƒ в точке с абсциссой хо.
а) ƒ(х) = хо – точка максимума (y =
б) ƒ(х) = хо – точка минимума (y =
Просмотр содержимого документа
«Практическая работа по теме "Производная" »
ПРАКТИЧЕСКАЯ РАБОТА
«Производная»
Учитель математики
Нагаева С.Н.
МАОУ «Лицей №1»
г. Березники
Пермский край
г. Березники, 2014 г.
ПРАКТИЧЕСКАЯ РАБОТА
«Система заданий по отработке учебных элементов:
1) умение находить производную функции, используя таблицу производных элементарных функций и правила нахождения производных;
2) умение вычислять значение производной в точке;
3) владение геометрическим смыслом производной».
I. Умение находить производную функции
1) Базовый уровень сложности задания
Найдите производную функции:
а) y = (4-3х)5 y' = -15(4-3х)4
б) y = ех + 6х2 y' = ех + 12х
в) y = 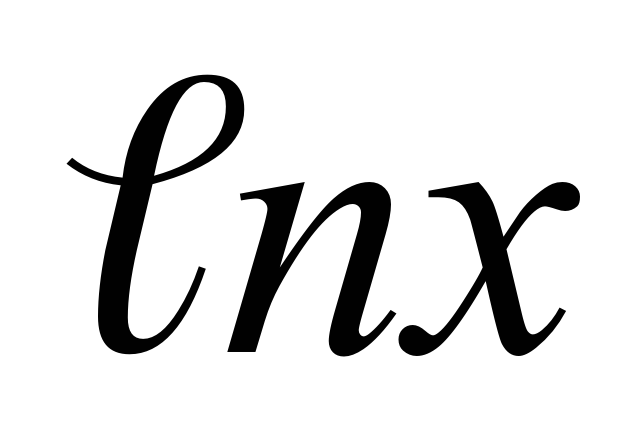 + 3sin x –
+ 3sin x –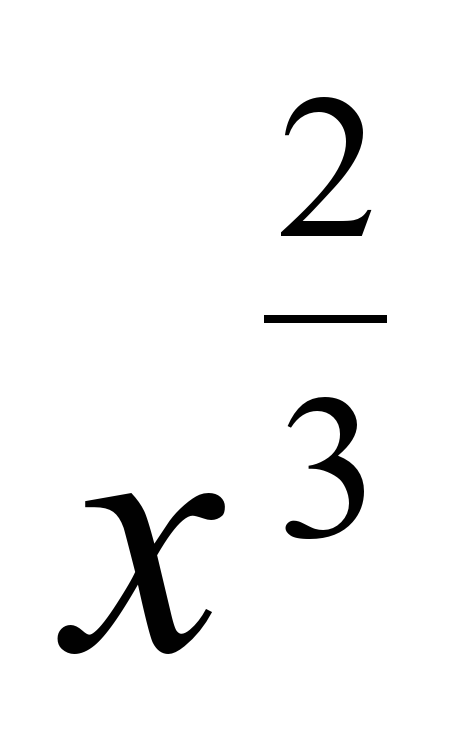 y' =
y' = 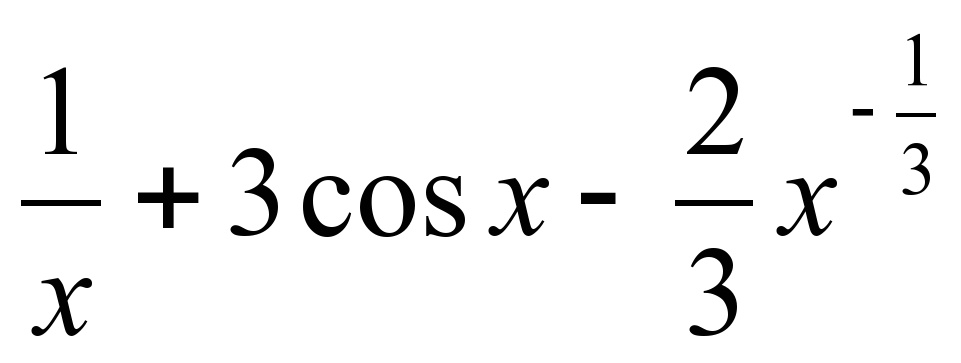
г) y = cos2 x y' = - sin2x
д) y = x6 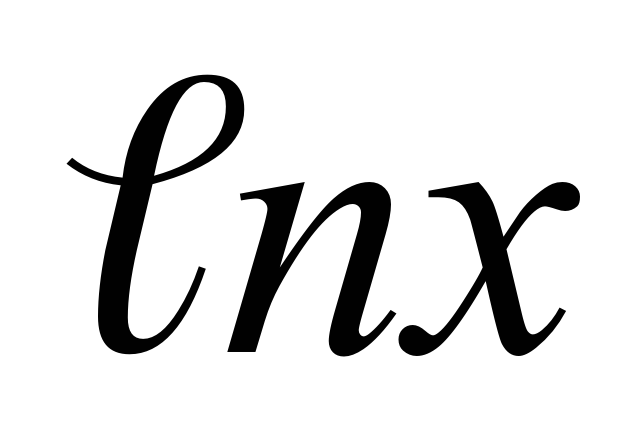 y' = x5 (6
y' = x5 (6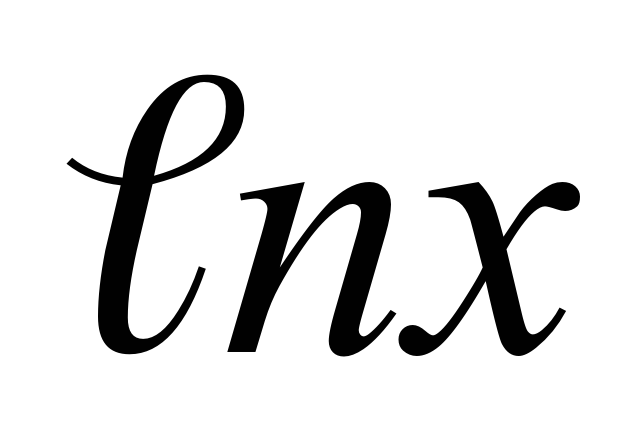 +1)
+1)
2) Повышенный уровень сложности задания
a) y= 3e2x - 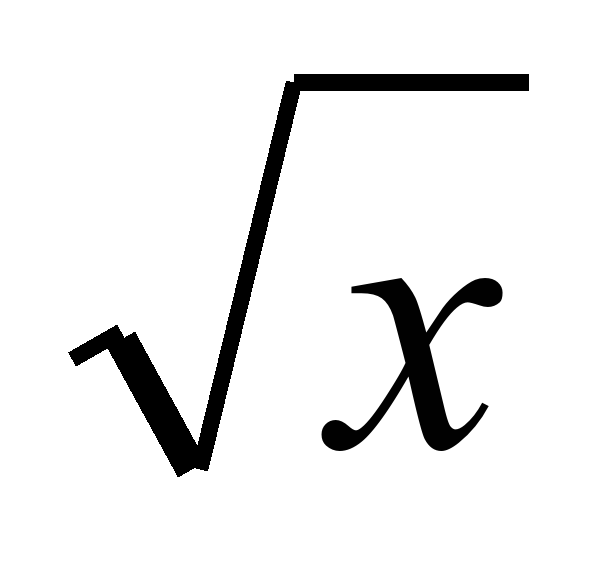 y' = 6e2x -
y' = 6e2x - 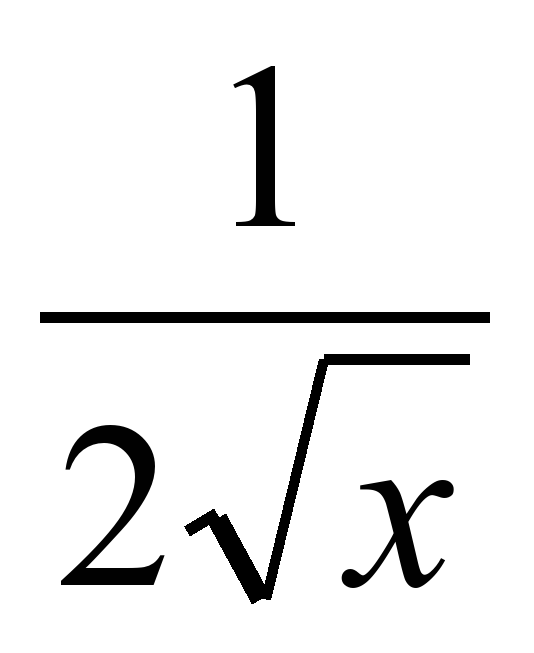

б) y = sin4x+cos5x+2x3 y'=4 sin3x cos x-5sin5x+6x2
в) y =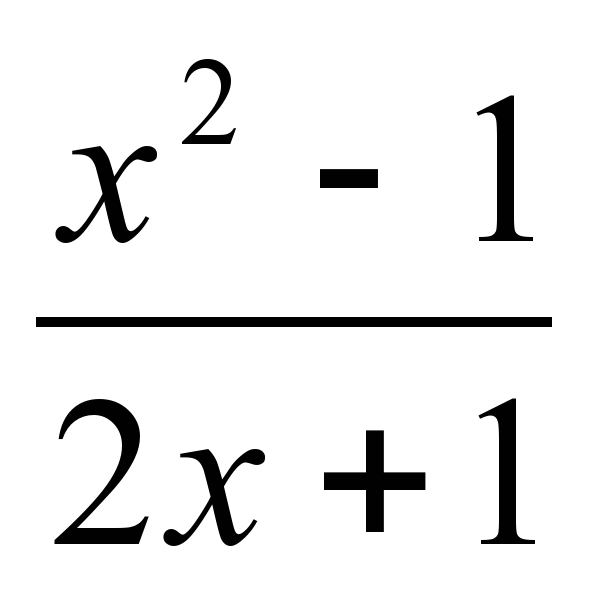 y' =
y' = 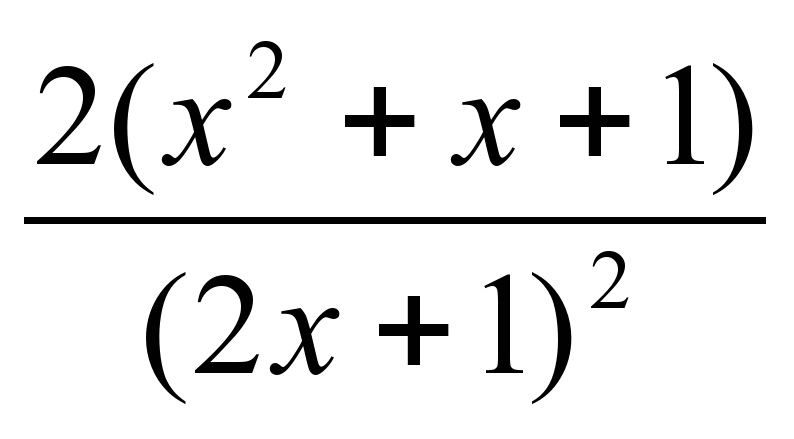
г) y = 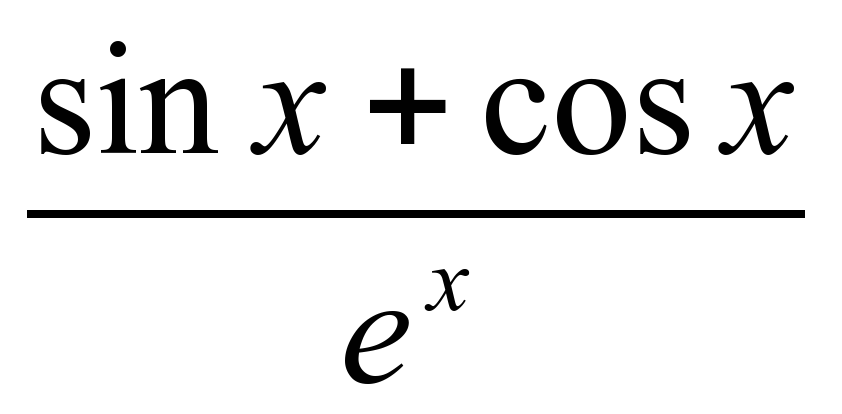 y' = -
y' = - 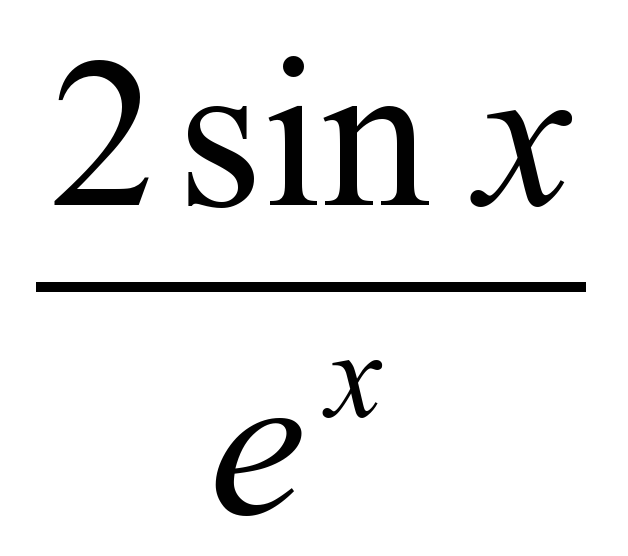
д) y = 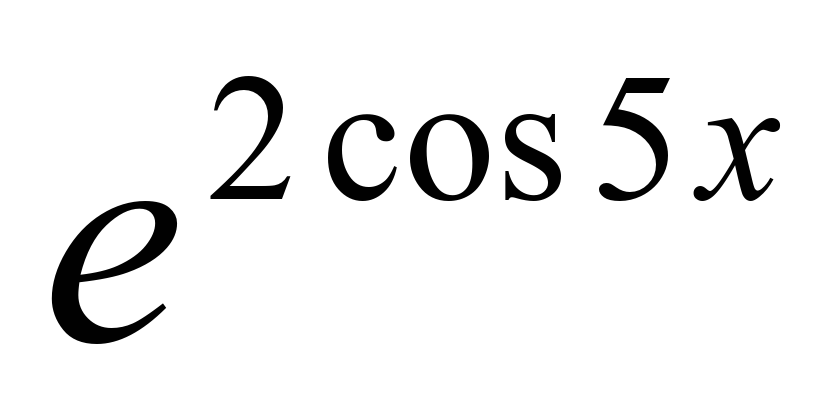 y' = -
y' = -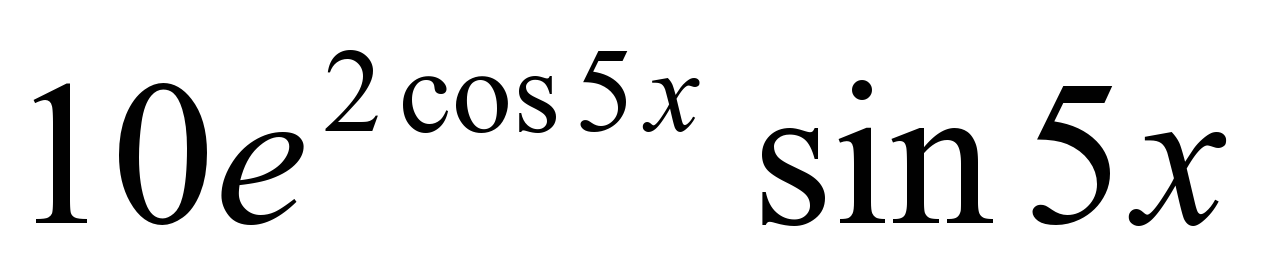

II. Умение вычислять значение производной в точке.
1) Базовый уровень сложности задания.
Найдите значение производной данной функции в точке хо:
а) y = (4-3x)6; xo = 1 (y' = -18(4-3x)5; -18)
б) y = x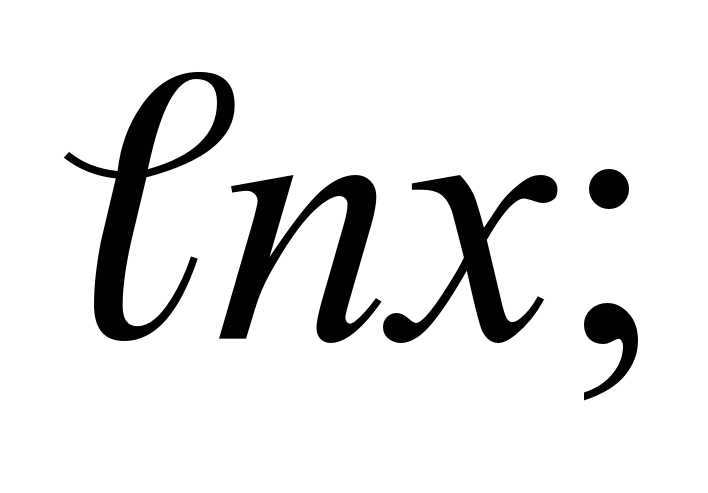 xo=2 (
xo=2 (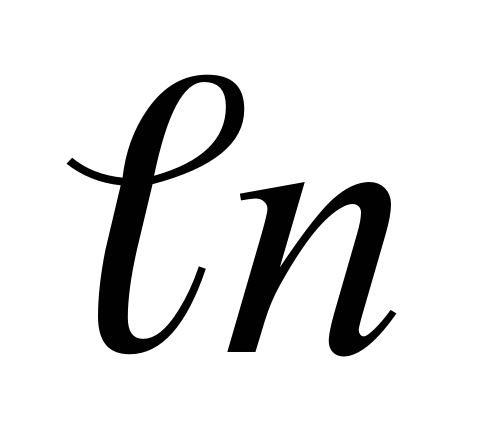 2+1)
2+1)
в) y = xsin (3x-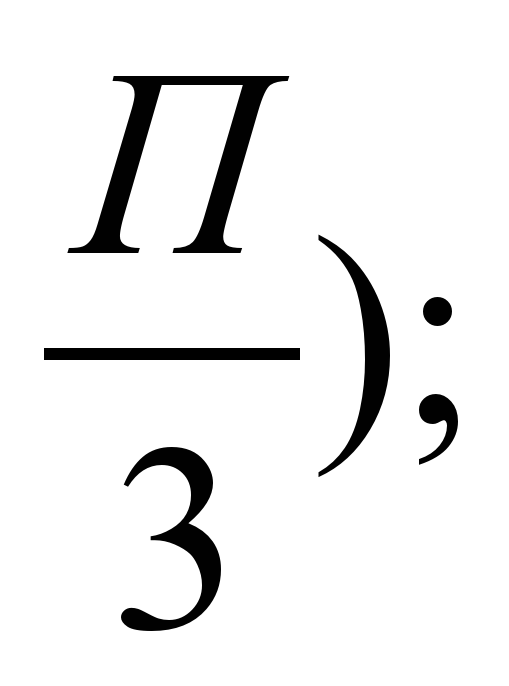 xo=
xo= 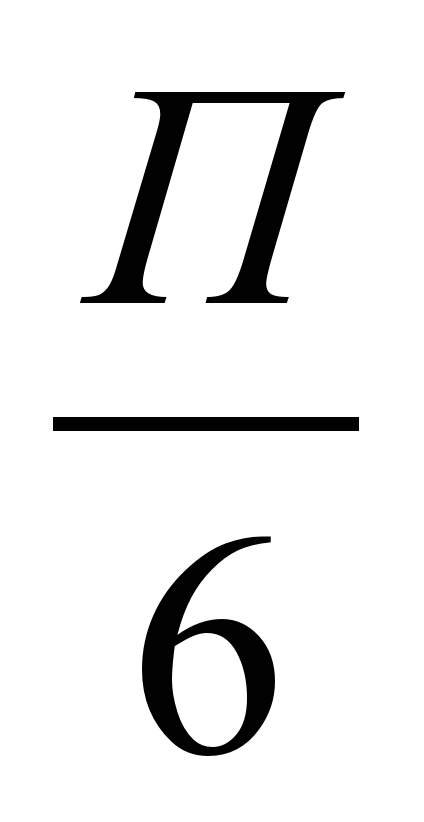 (
(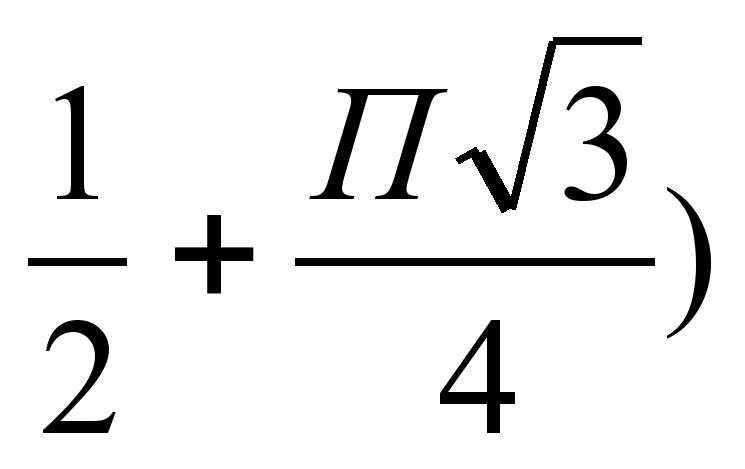
2) Повышенный уровень сложности задания
а) y = 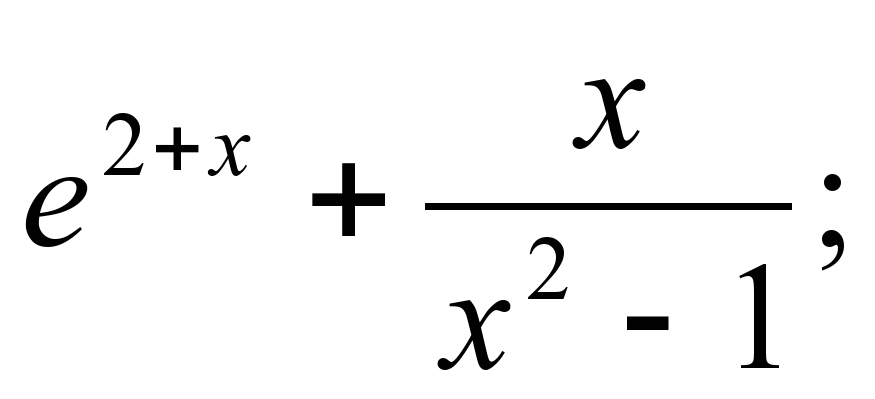 xo = -2 (
xo = -2 (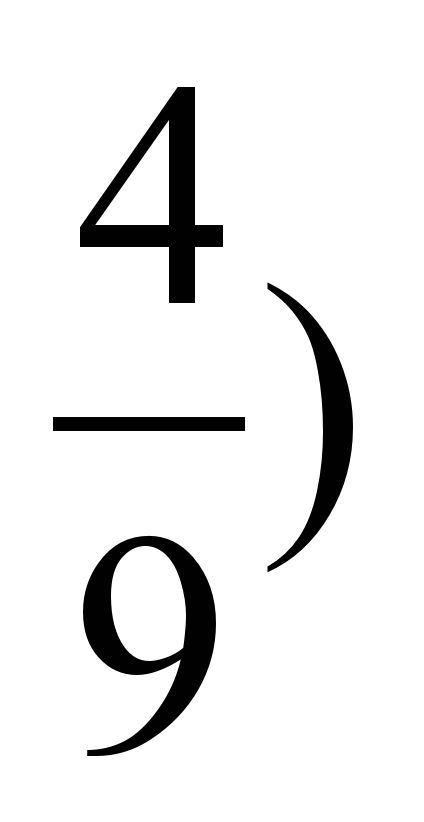
б) y = 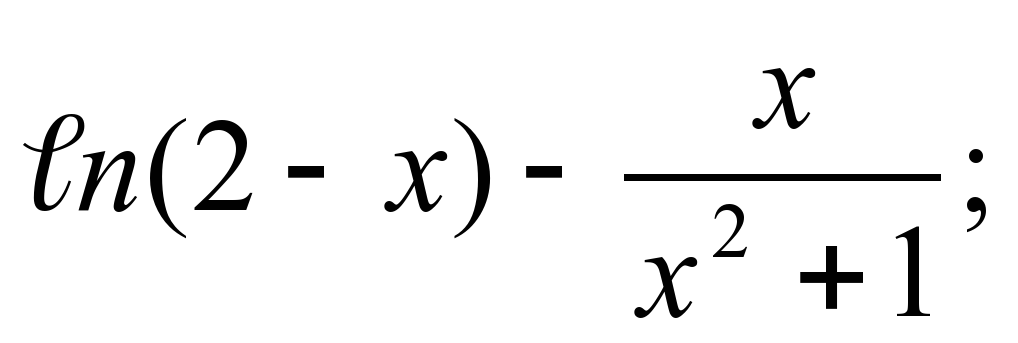 xo = -1 (-
xo = -1 (- 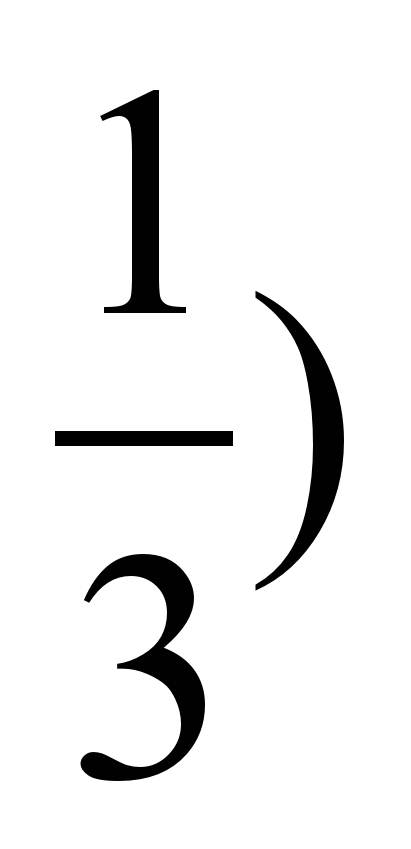
в) Найдите значения а и в, при которых выполняются данные условия:
y=a sin4x+в cos2x; y' (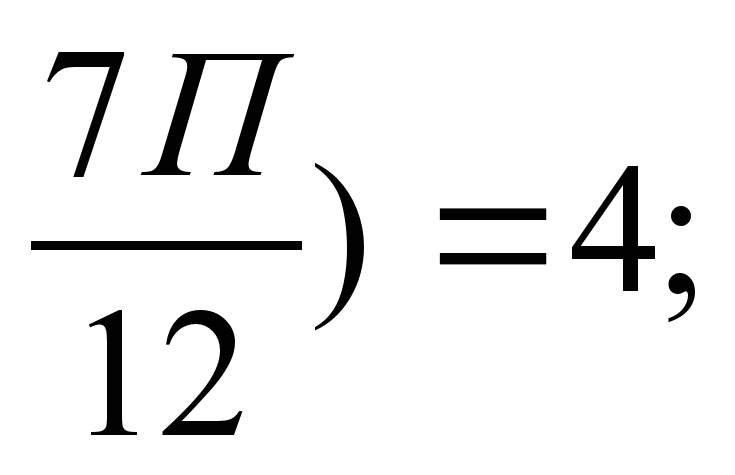 y' (
y' (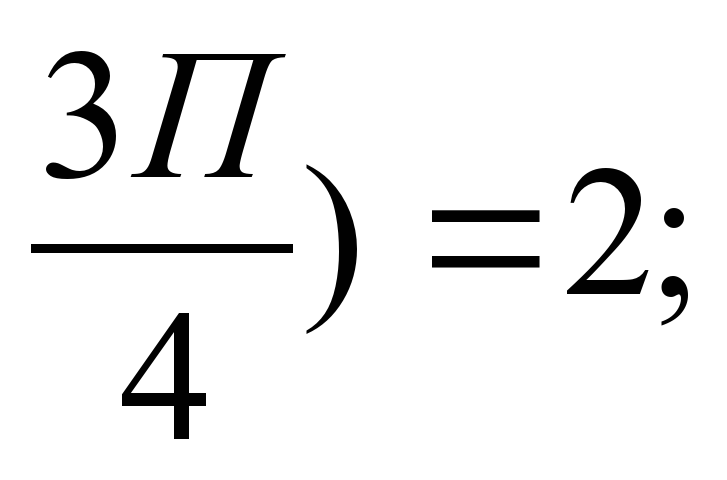 (a=
(a=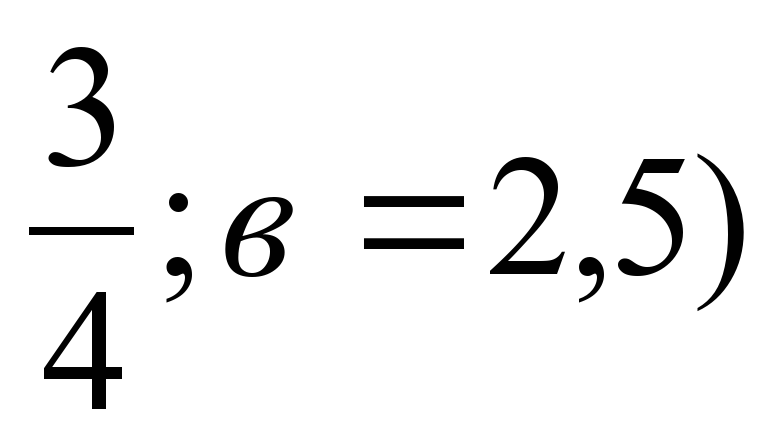
г) y = a sin2x + в cos x; y' (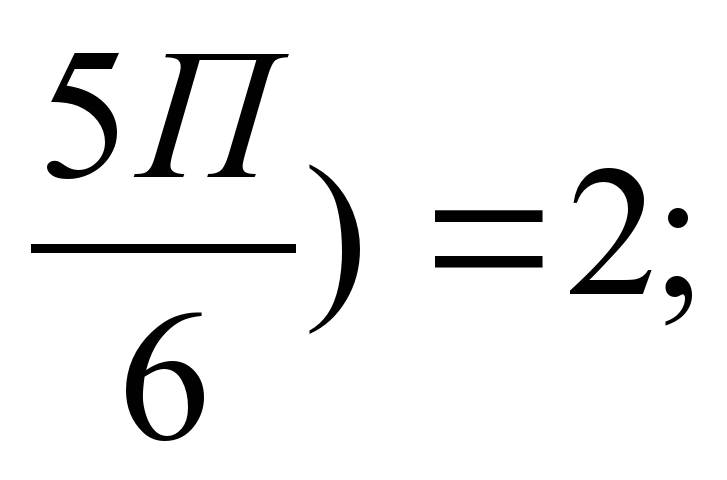 y' (
y' (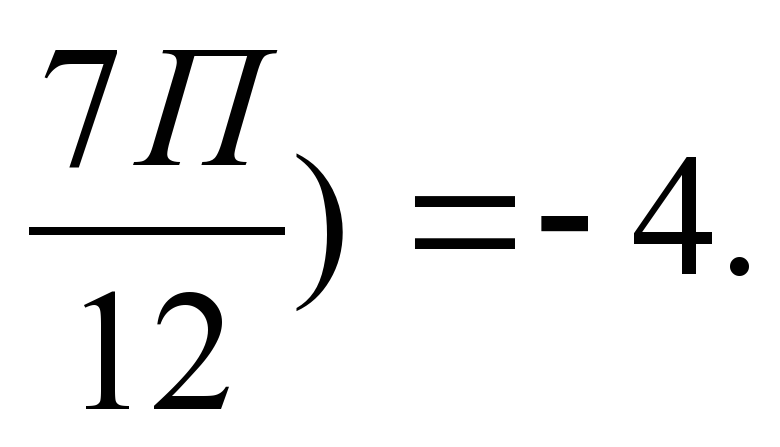 (a=o; в = -4).
(a=o; в = -4).
3) Высокий уровень сложности задания.
Для функции y = 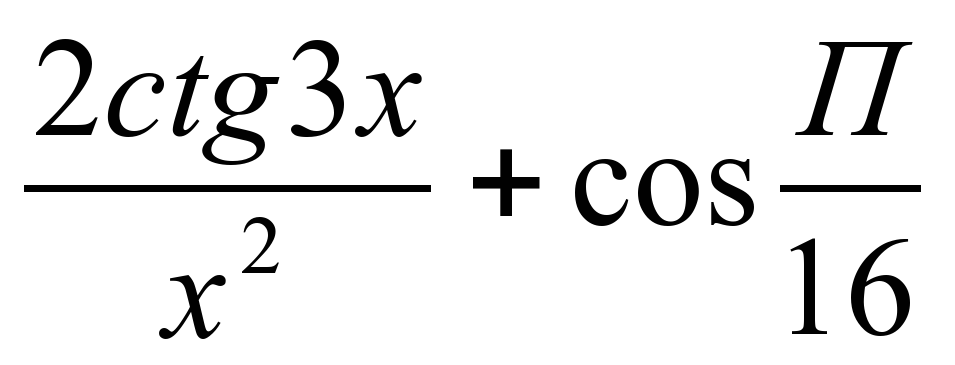 найдите производную в точке
найдите производную в точке
хо =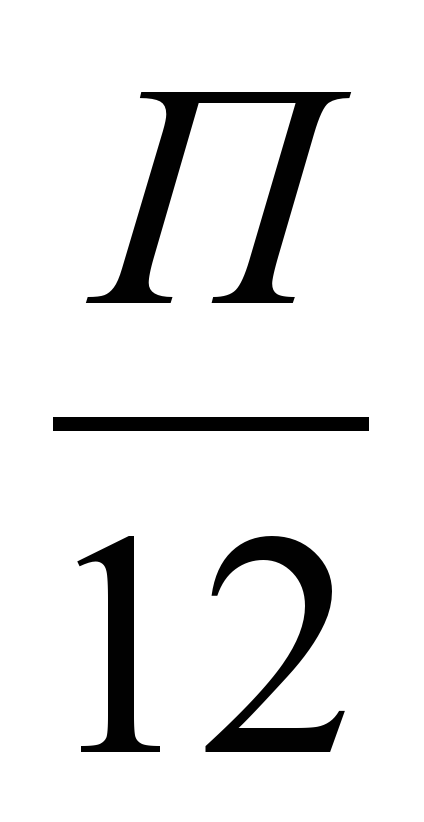 (-
(-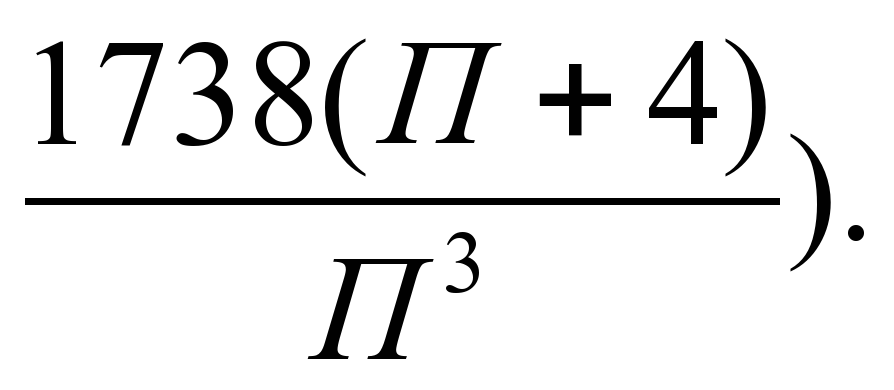
III. Владение геометрическим смыслом производной.
Базовый уровень.
Напишите уравнение касательной к графику функции ƒ в точке с абсциссой хо:
а) ƒ х)= х3 – 3х2; хо= -1 y = 9x+5
б) ƒ(х) =-х3 + х – 1; хо =-2 y = -11x-17
в) ƒ(х) = 2х2-5х+1; хо = 2 y = 3x-7
г) ƒ(х) = 3х2 – 4х – 2; хо = -1 y = -10x-5
2) Повышенный уровень.
Напишите уравнение касательной к графику функции ƒ в точке с ординатой yo:
а) ƒ(х) = 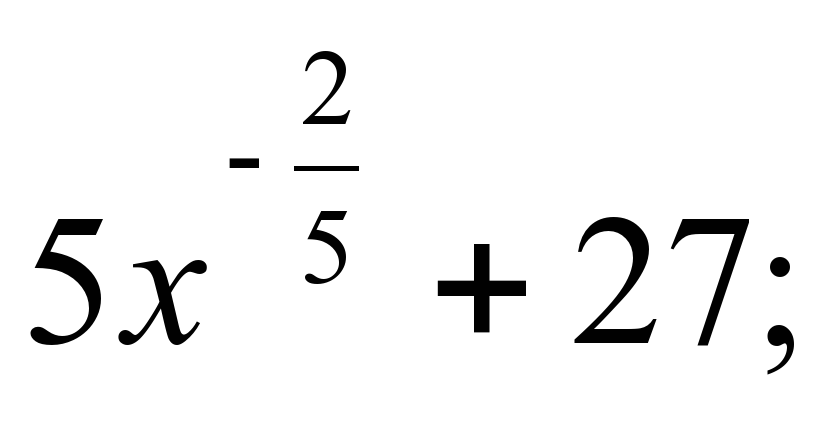 yo = 32 y = -2x + 34
yo = 32 y = -2x + 34
б) ƒ(х) = 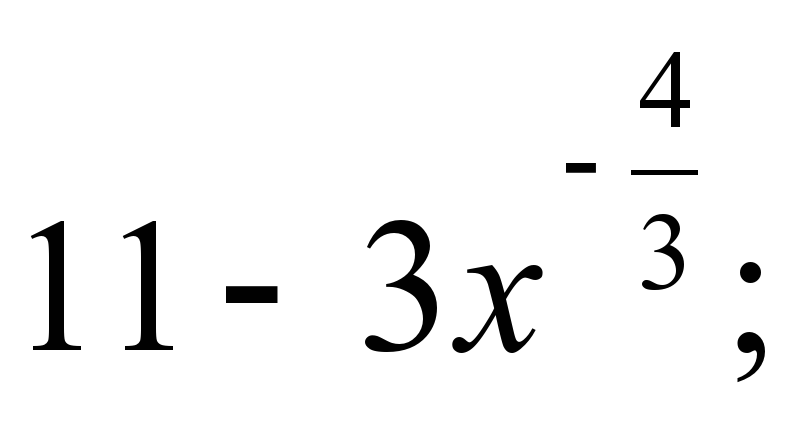 yo = 8 y = 4x+4
yo = 8 y = 4x+4
в) При каком значении а данная прямая является касательной к графику функции ƒ
y = a x-5; ƒ(x)=3x2-4x-2. (a = -10; a = 2)
3) Высокий уровень
Составьте уравнение касательной к графику функции ƒ в точке с абсциссой хо.
а) ƒ(х) = 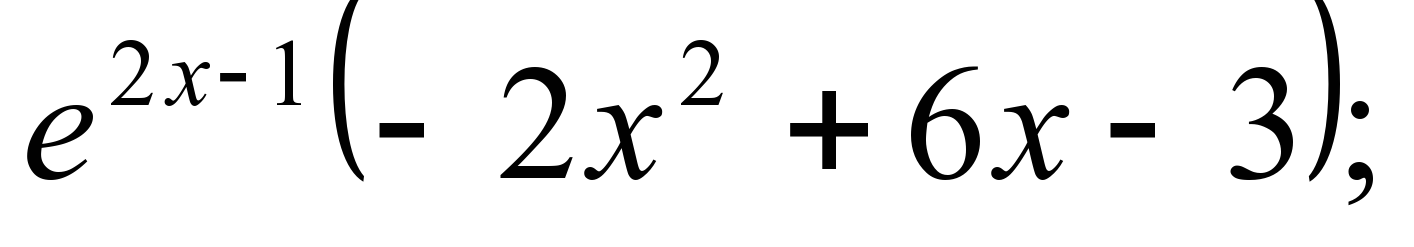 хо – точка максимума (y =
хо – точка максимума (y = 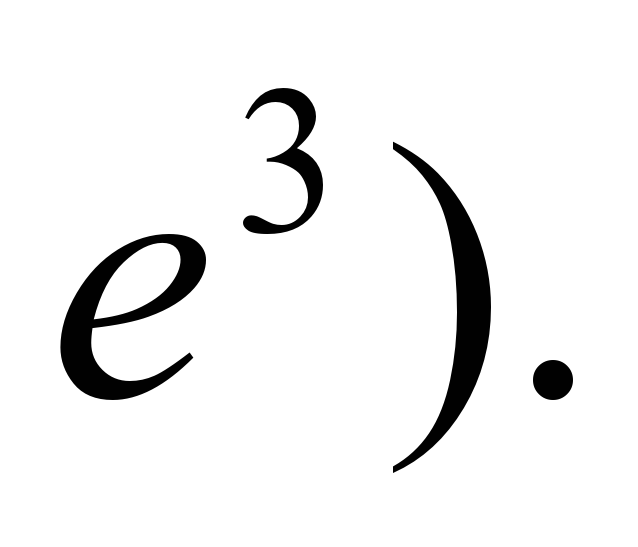
б) ƒ(х) = 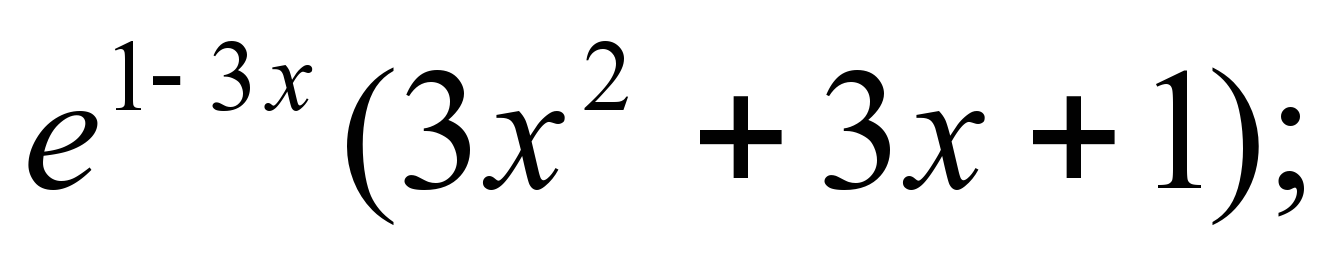 хо – точка минимума (y =
хо – точка минимума (y =