Математика 2 курс
Практическая работа № 8.
Тема: Вычисление объемов тел вращения.
Цель: Отработать навыки нахождения определенного интеграла. Научиться находить объемы тел вращения.
Теоретический материал
Вычисление объема тела по известным площадям поперечных сечений.
Если площадь сечения тела плоскостью, перпендикулярной оси Ox, может быть выражена как функция от x, т.е. в виде  , то объем части тела, заключенной между перпендикулярными оси Ox плоскостями x = a и x = b, находится по формуле
, то объем части тела, заключенной между перпендикулярными оси Ox плоскостями x = a и x = b, находится по формуле 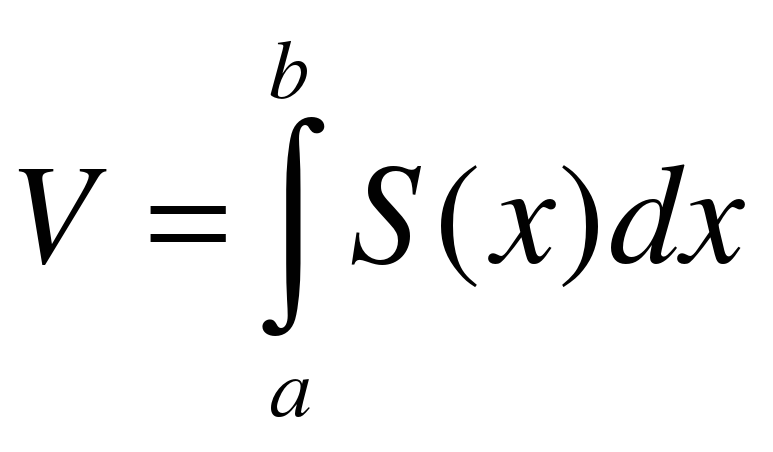 .
.
Вычисление объема тела вращения.
Если криволинейная трапеция, ограниченная кривой 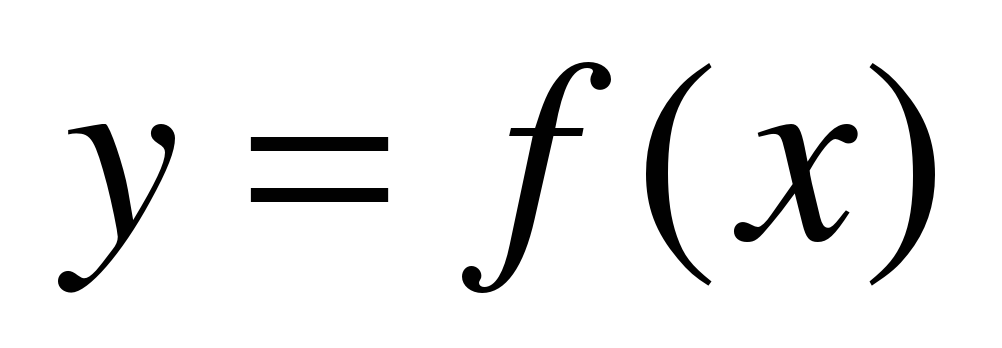 и прямыми у = 0, х = а, x = b вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле
и прямыми у = 0, х = а, x = b вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле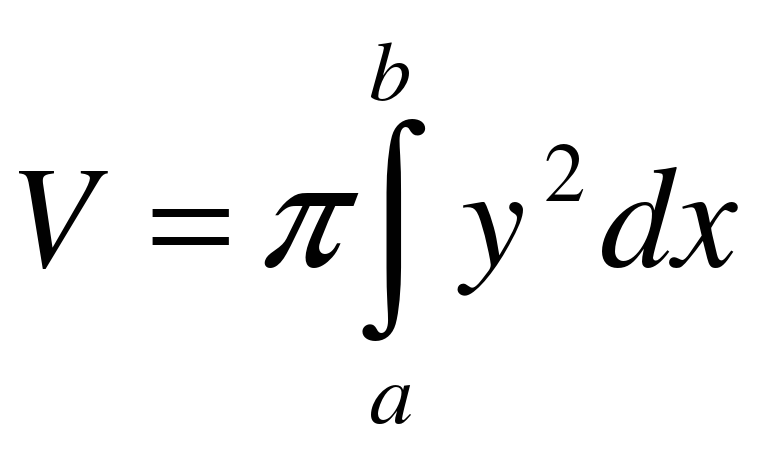 .
.
Если фигура, ограниченная кривыми 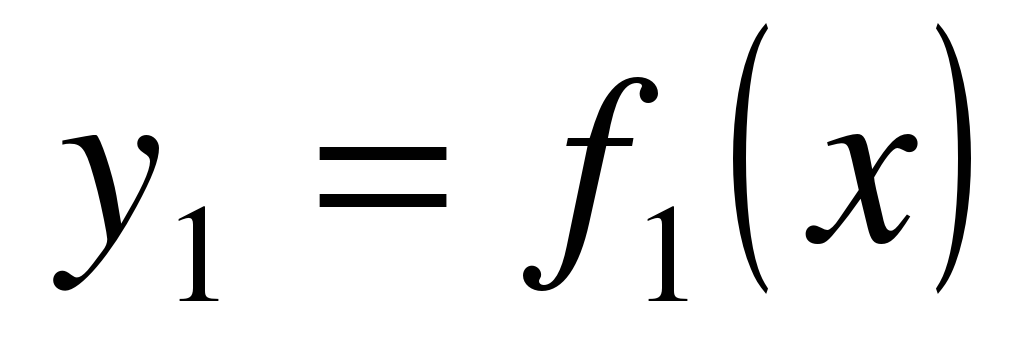 и
и 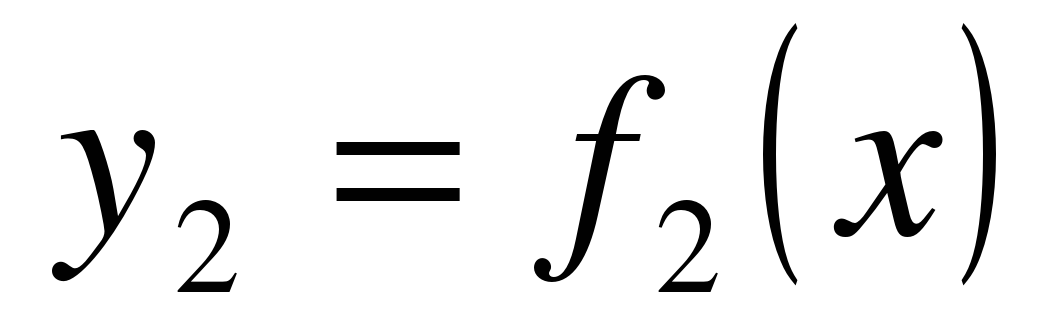
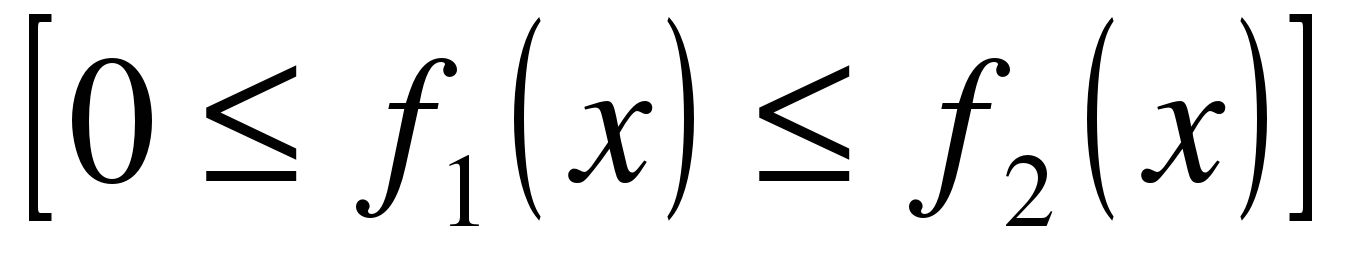 и прямыми x = a, x = b, вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле
и прямыми x = a, x = b, вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле 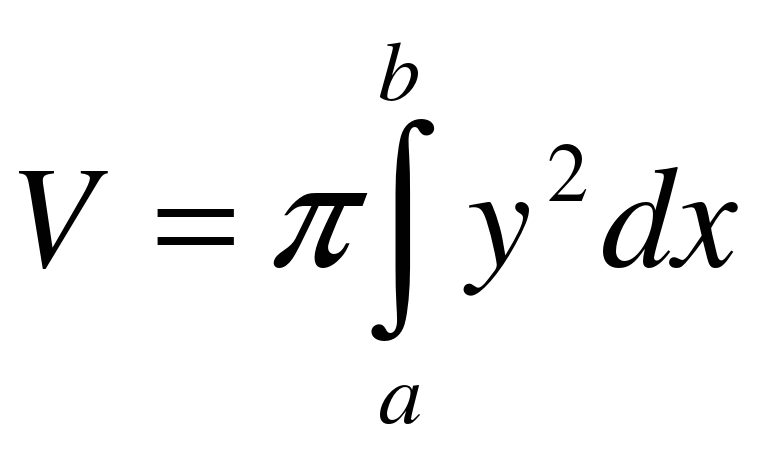 .
.
Примеры.
Пример 1. Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями у = 2х + 1, у = х + 4, х=0 и х=1.
Р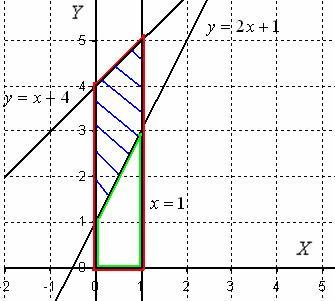 ешение: Изобразим на чертеже плоскую фигуру, ограниченную линиями у = 2х + 1, у = х + 4, х = 0 и х = 1, не забывая при этом, что уравнение х = 0 задает ось Оу.
ешение: Изобразим на чертеже плоскую фигуру, ограниченную линиями у = 2х + 1, у = х + 4, х = 0 и х = 1, не забывая при этом, что уравнение х = 0 задает ось Оу.
Искомая фигура заштрихована синим цветом. Объем тела вращения вычислим как разность объемов тел.
Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси Ох получается усеченный конус. Обозначим объем этого усеченного конуса через V1.
Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси Ох, то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через V2.
И, очевидно, разность объемов V = V1 – V2 – в точности объем искомой фигуры.
Используем формулу для нахождения объема тела вращения: 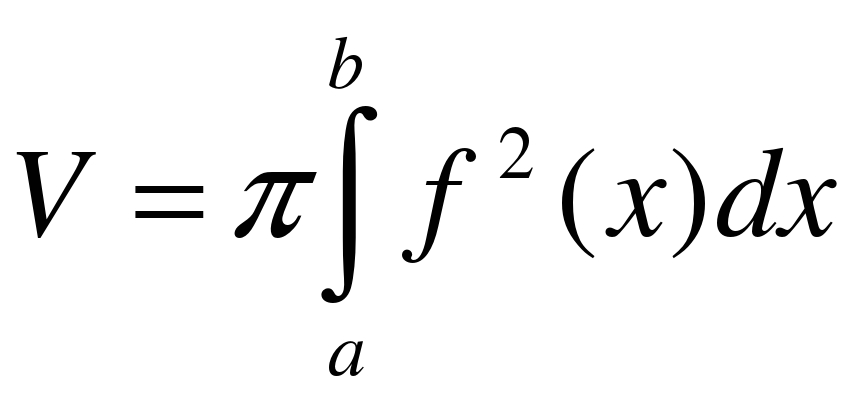
1) Фигура, обведенная красным цветом ограничена сверху прямой y = x + 4, поэтому: 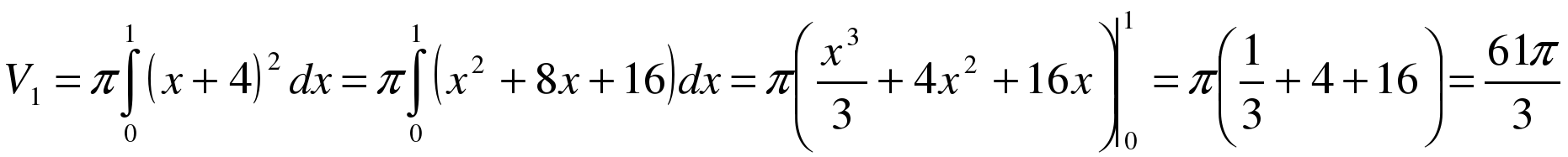 .
.
2) Фигура, обведенная зеленым цветом ограничена сверху прямой y = 2x + 1, поэтому:  .
.
3) Объем искомого тела вращения: 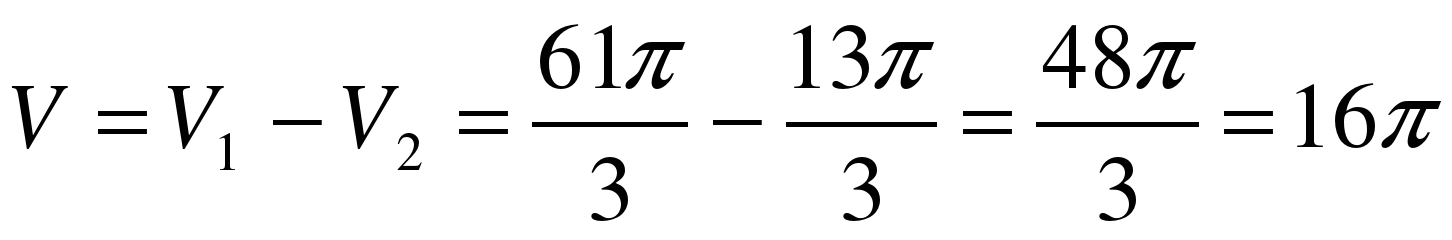 .
.
Ответ: 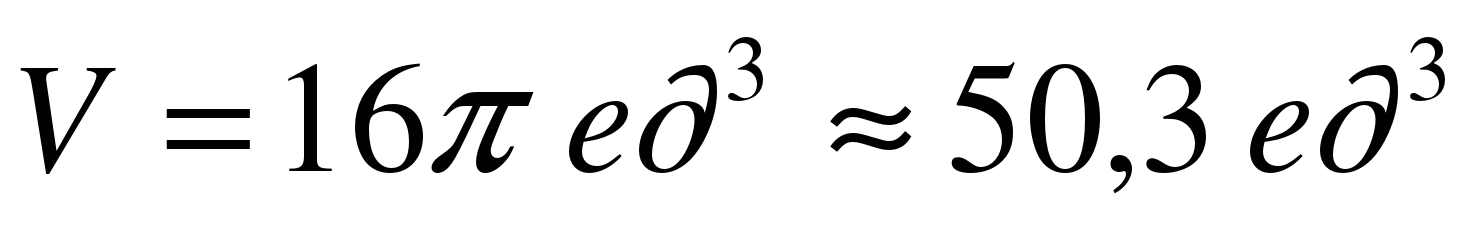 .
.
Пример 2. Вычислить объем тела, образованного вращением относительно оси Ox плоской фигуры, ограниченной линиями 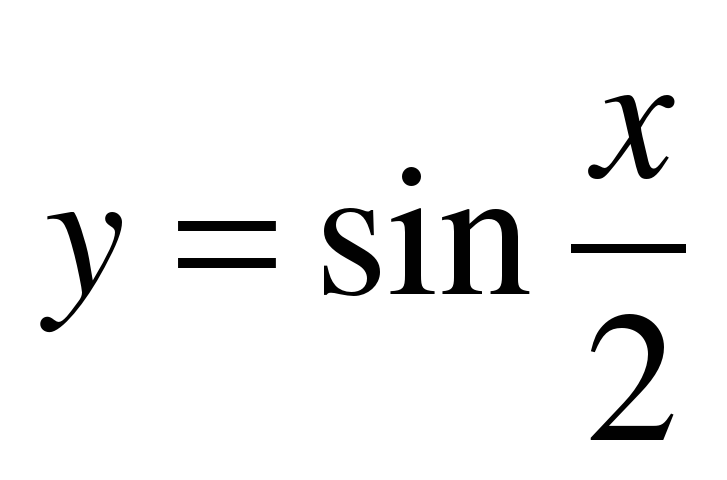 ,
, 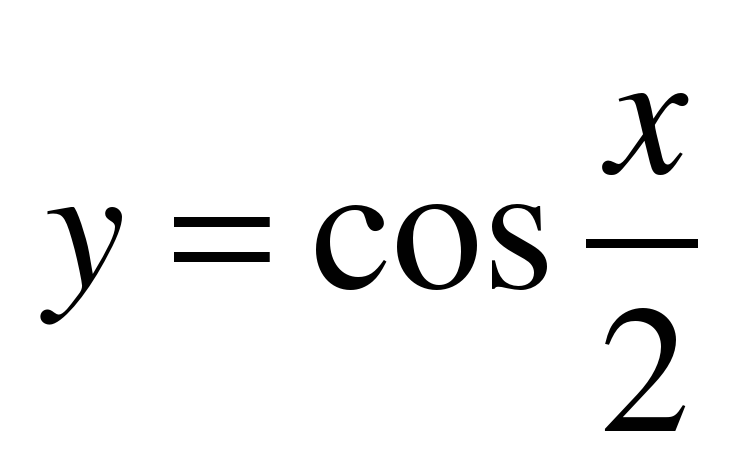 , где
, где 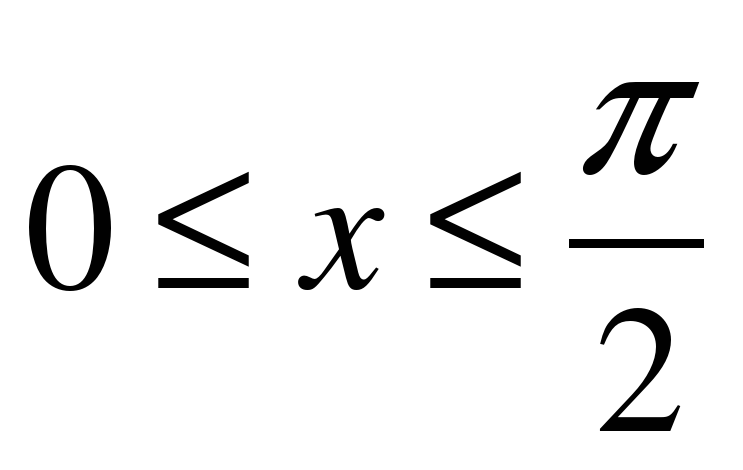 .
.
Р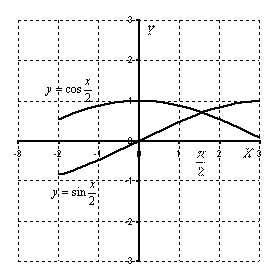 ешение: Выполним чертеж:
ешение: Выполним чертеж:
Объем тела вращения вычислим как разность объемов при помощи формулы: 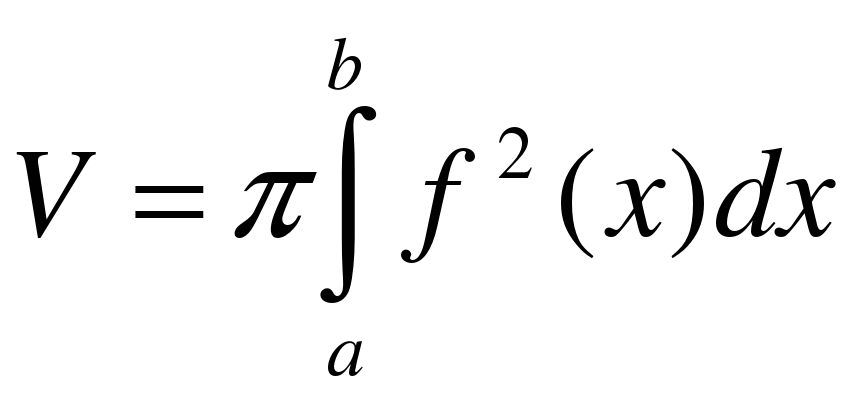 .
.
В данном случае:
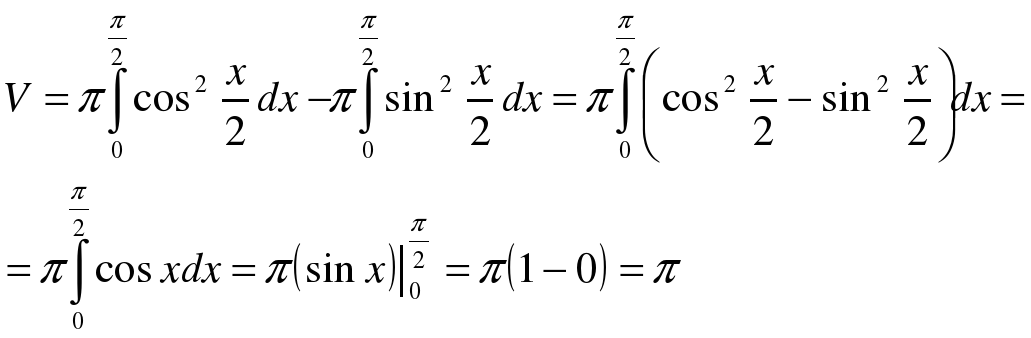
Ответ: V = π ед3. ≈ 3,14 ед3.
Пример 3. Дана плоская фигура, ограниченная линиями 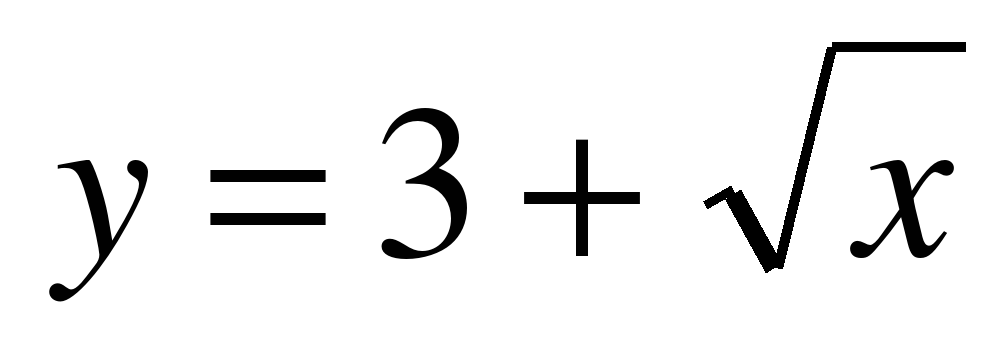 ,
, 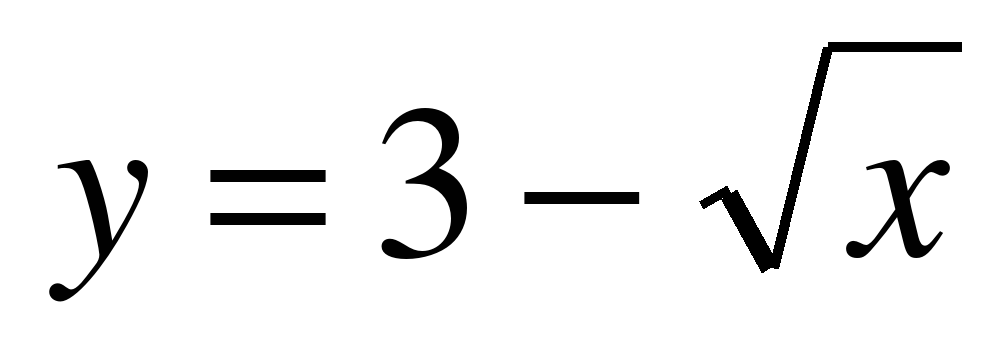 ,
, 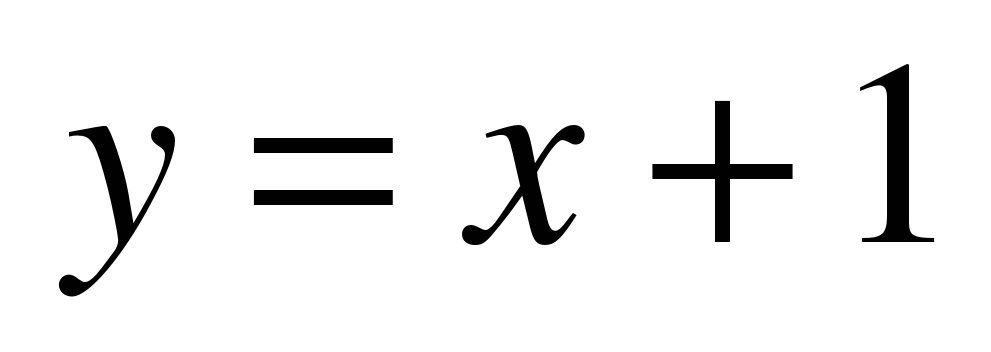 .
.
1) Найти площадь плоской фигуры, ограниченной данными линиями.
2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу.
Решение: Задача состоит из двух частей. Начнем с площади.
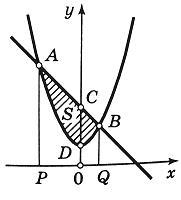
1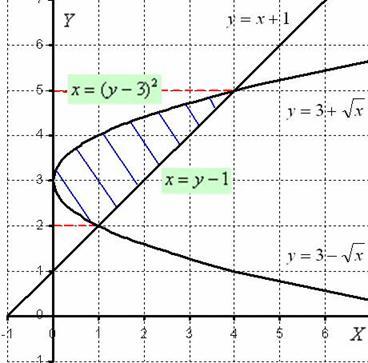 ) Выполним чертёж:
) Выполним чертёж:
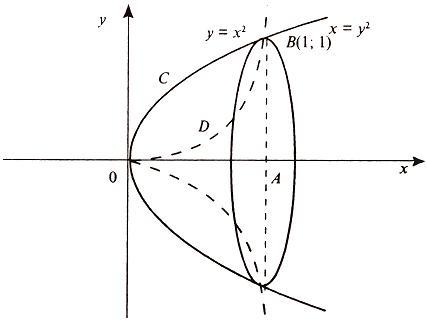
Легко заметить, что функция 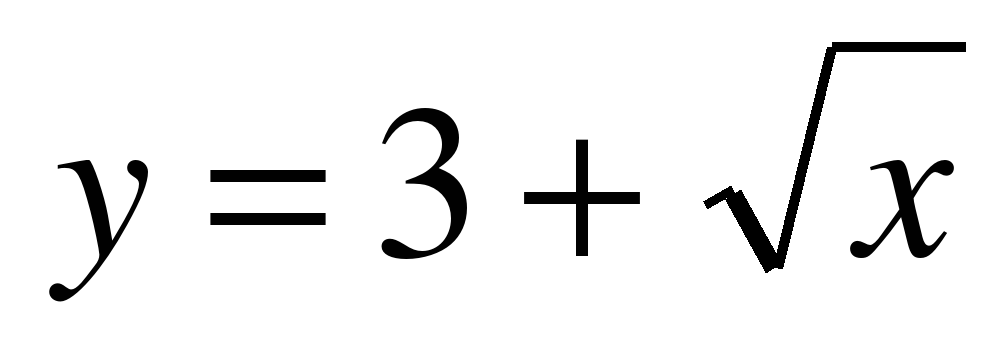 задает верхнюю ветку параболы, а функция
задает верхнюю ветку параболы, а функция 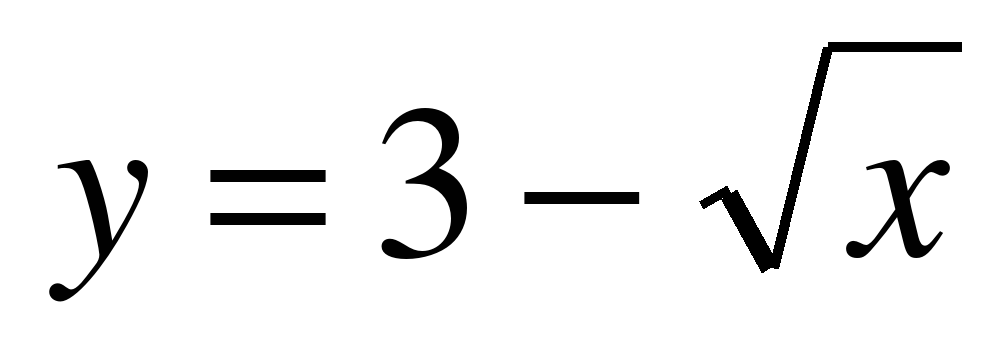 – нижнюю ветку параболы.
– нижнюю ветку параболы.
Нужная фигура, площадь которой предстоит найти, заштрихована синим цветом.
Применим более рациональный путь решения: он состоит в переходе к обратным функциям и интегрированию по оси Оу.
Для параболы:
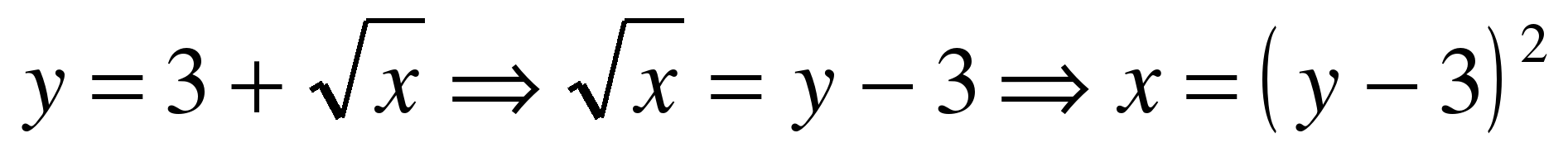
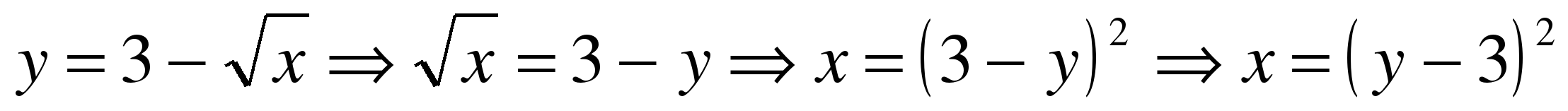
Для прямой: 
Теперь смотрим на ось Оу.
пожалуйста, периодически наклоняйте голову вправо на 90 градусов по ходу объяснений!
Нужная нам фигура лежит на отрезке [2; 5], который обозначен красным пунктиром. При этом на отрезке [2; 5] прямая х = у - 1 расположена выше параболы 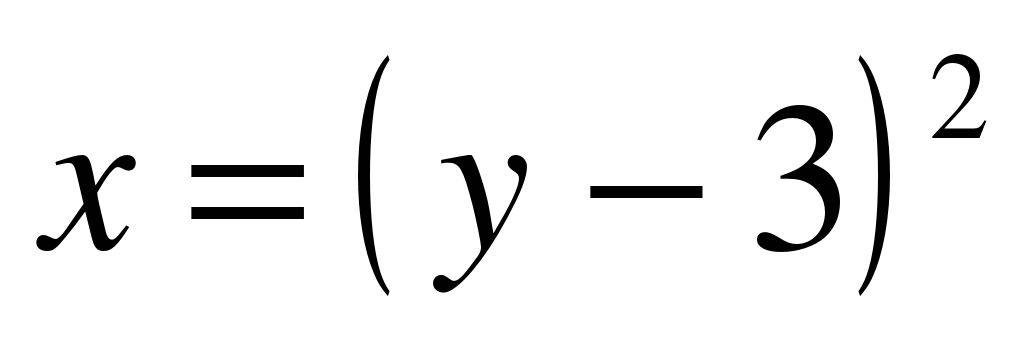 , а значит, площадь фигуры следует найти по формуле:
, а значит, площадь фигуры следует найти по формуле: 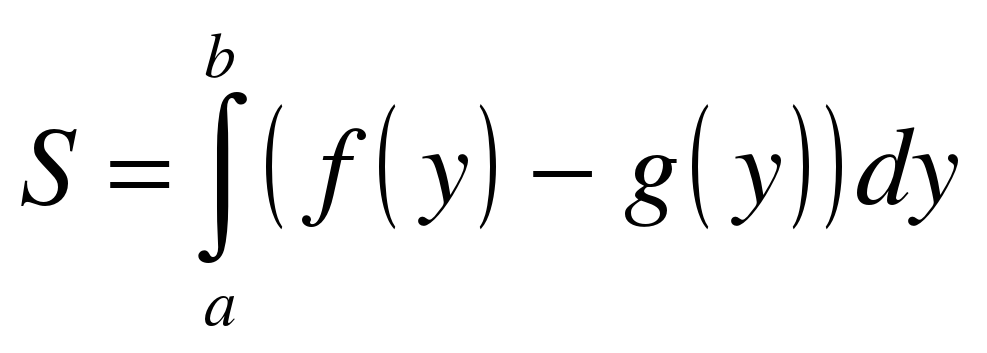 .
.
! Примечание: Пределы интегрирования по оси Оу следует расставлять строго снизу вверх!
Находим площадь:
На отрезке [2; 5] 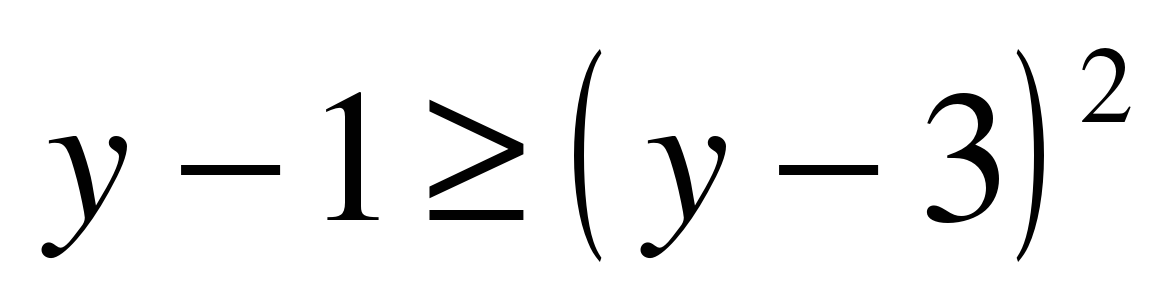 , поэтому:
, поэтому: 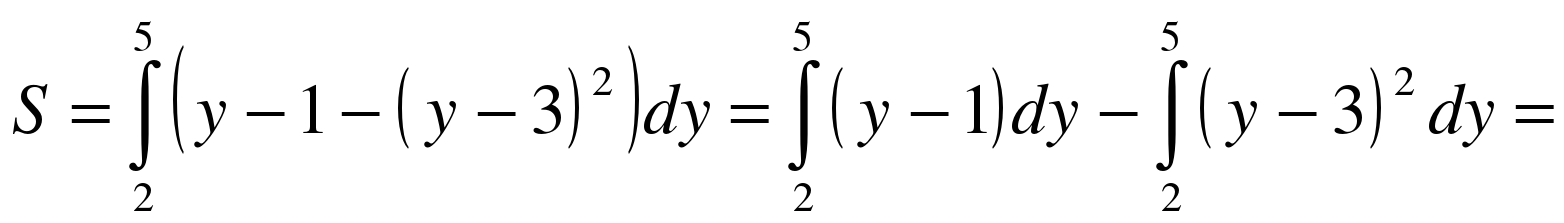
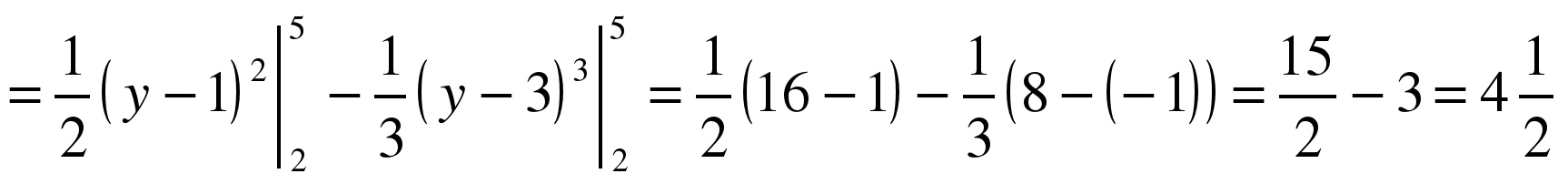 .
.
Ответ: 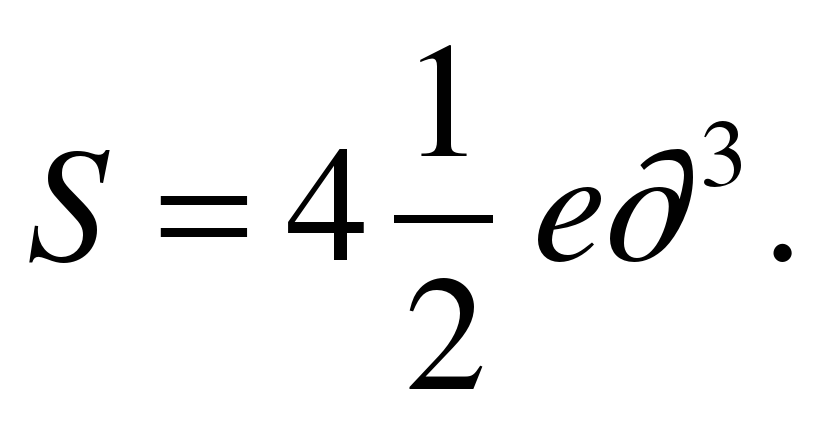
2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси Оу.
Перерисую чертеж немного в другом оформлении.
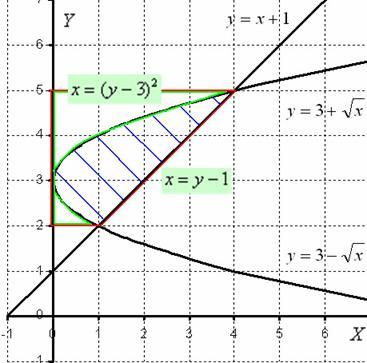
Итак, фигура, заштрихованная синим цветом, вращается вокруг оси Оу. В результате получается «зависшая бабочка», которая вертится вокруг своей оси.
Для нахождения объема тела вращения будем интегрировать по оси Оу.
Очевидно, что объем тела вращения, следует найти как разность объемов.
Вращаем фигуру, обведенную красным цветом, вокруг оси Оу, в результате получается усеченный конус. Обозначим этот объем через V1.
Вращаем фигуру, обведенную зеленым цветом, вокруг оси Оу и обозначаем через V2 объем полученного тела вращения.
Объем нашей «бабочки» равен разности объемов V = V1 – V2.
Используем формулу для нахождения объема тела вращения: 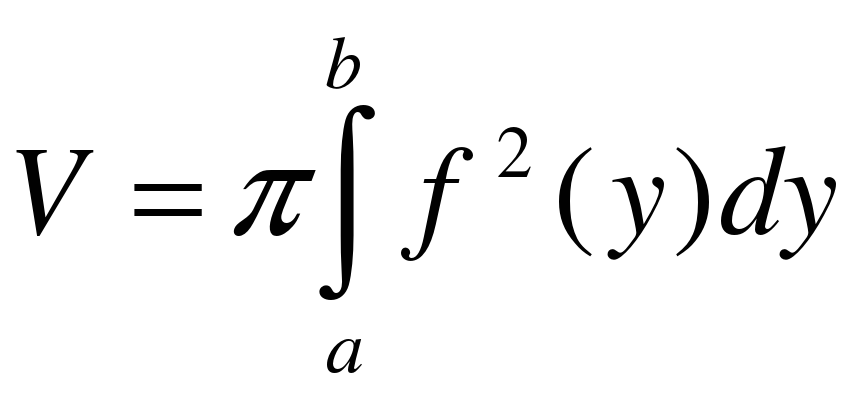 .
.
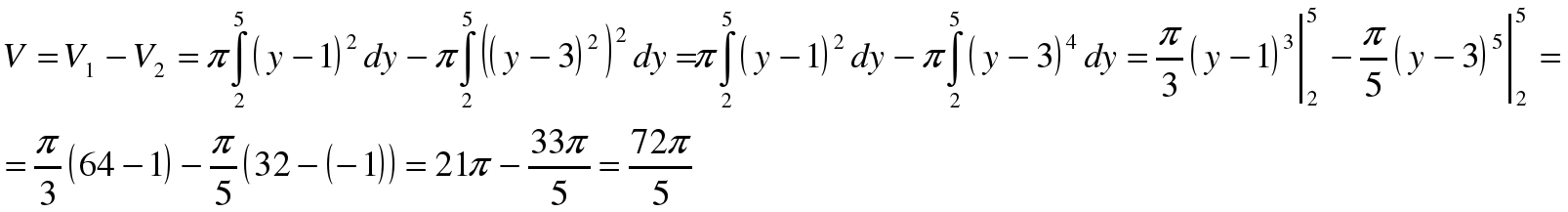
Ответ: 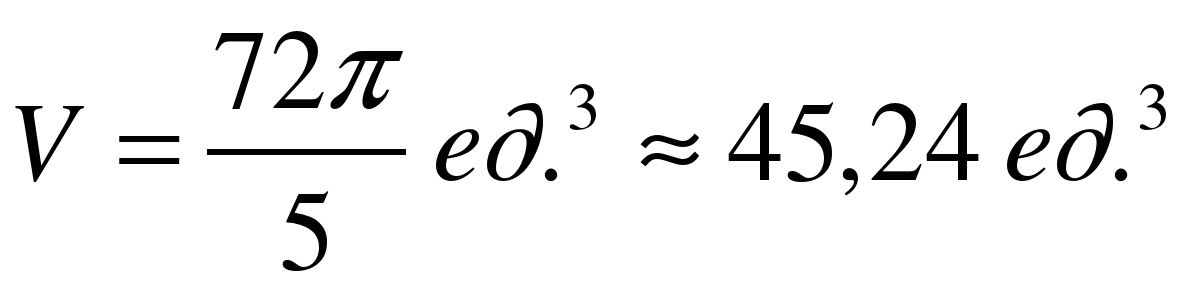
Пример 4. Плоская фигура ограничена графиком параболы 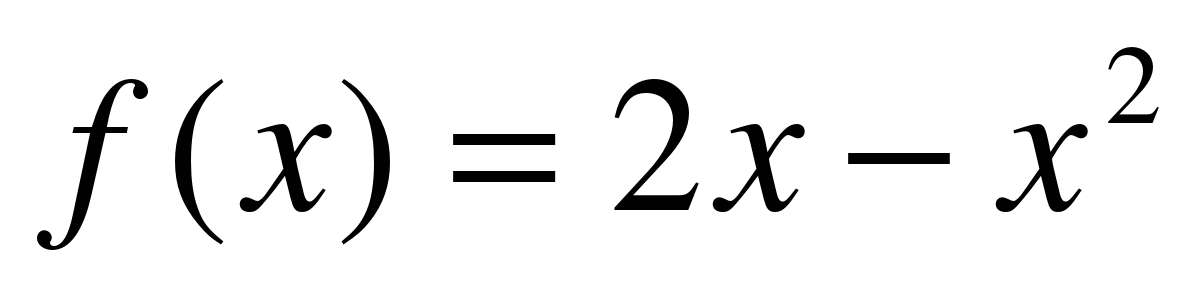 .Вычислить объем тела вращения.
.Вычислить объем тела вращения.
Решение: Вычислим объем тела вращения, используя данную формулу:
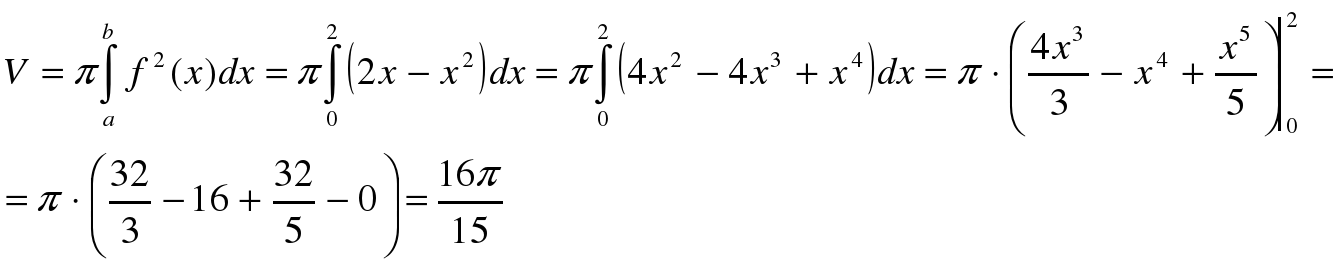
 .
.
Ответ: 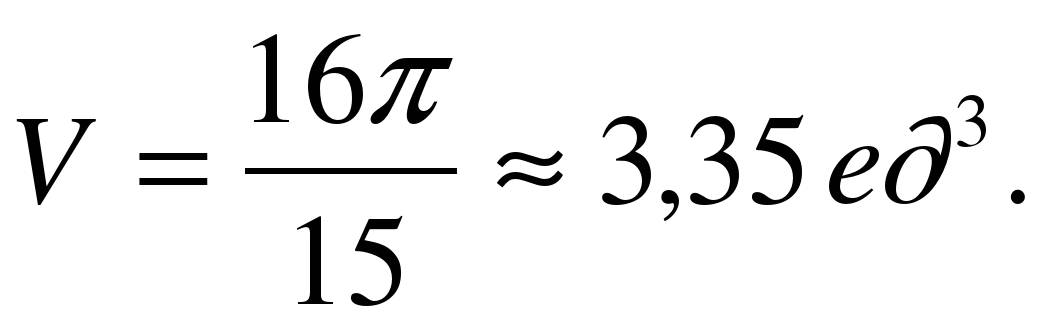
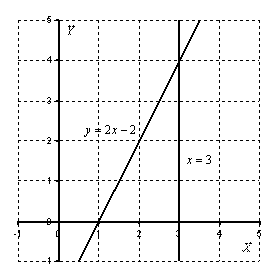
Пример 5. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 2х – у – 2 = 0, у=0, х=3.
Решение: Выполним чертеж. Объем тела вращения:
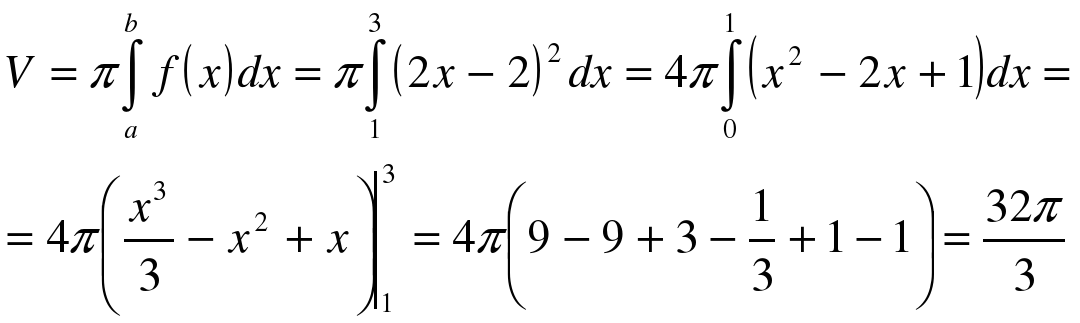
Ответ: 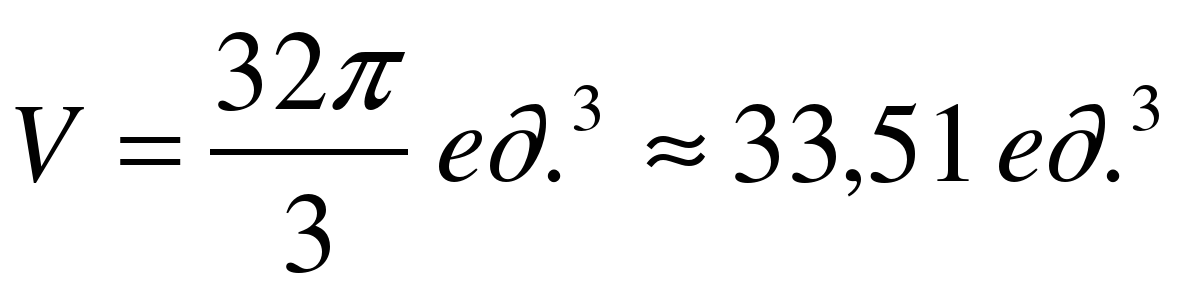
Пример 6. Дана плоская фигура, ограниченная линиями x = 2, 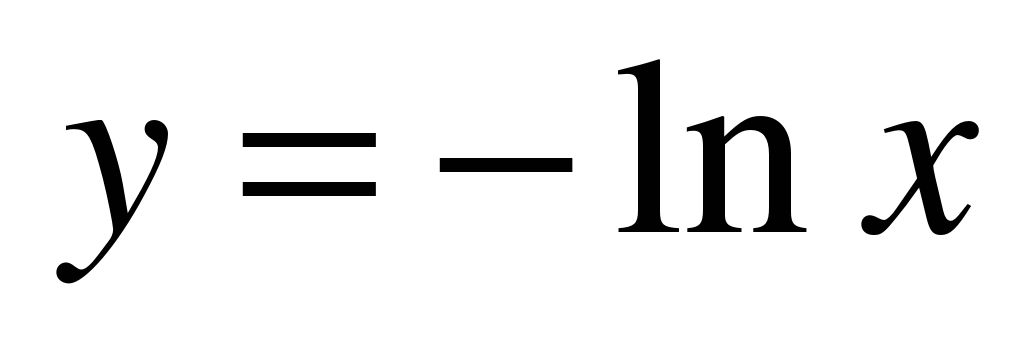 и осью Ox.
и осью Ox.
a) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной y.
б) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу.
Р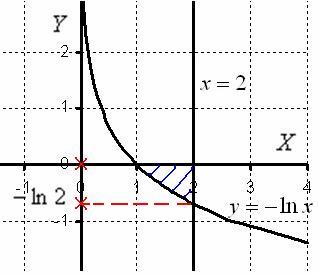 ешение:
ешение:
1) Выполним чертёж.
Перейдем к обратной функции: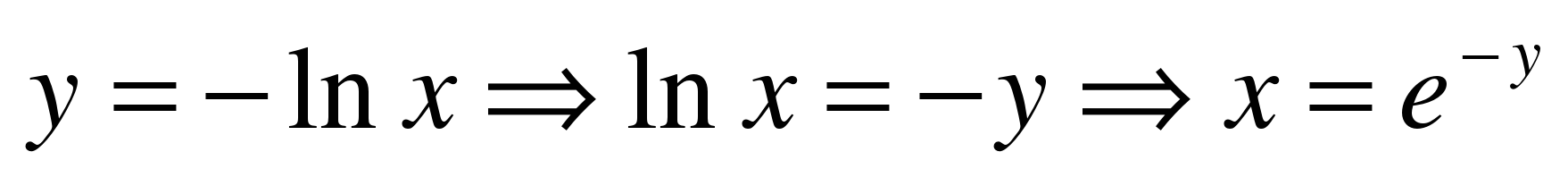
На отрезке [- ln 2; 0] 2 ≥ e-y, поэтому:
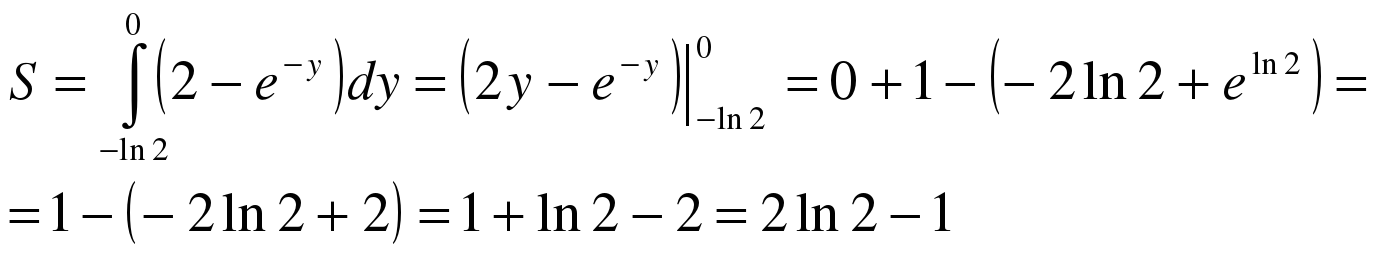
Ответ: 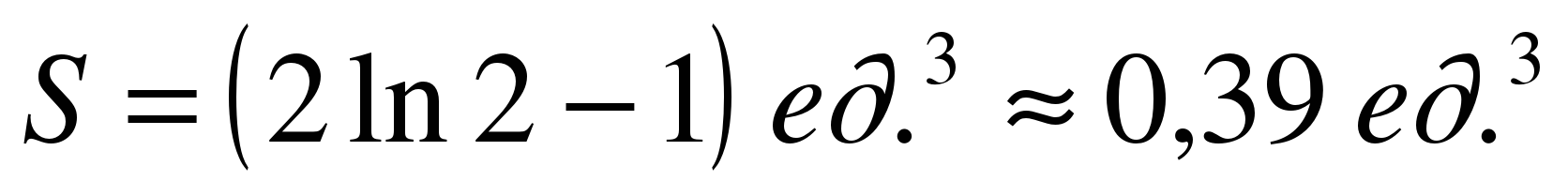
2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси Oy.
Объем тела вращения найдем как разность объемов тел вращения при помощи формулы 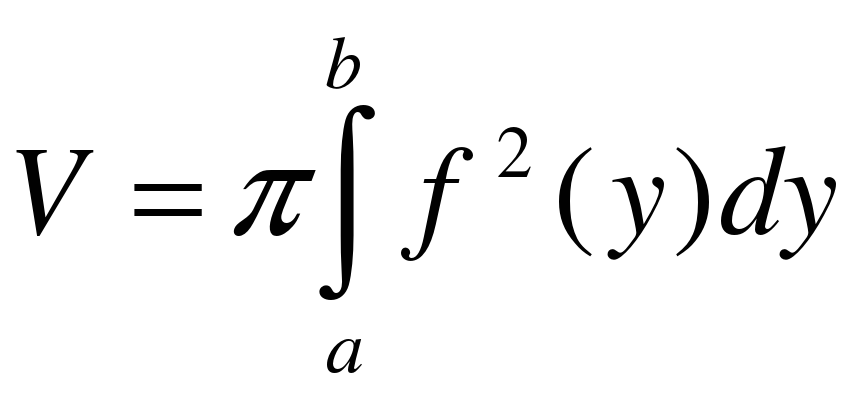 :
:
Ответ:
Задания для самостоятельной работы по теме:
| Вариант 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 2х – у – 2 = 0, у=0, х=7. 3. Дана плоская фигура, ограниченная линиями x = 4, 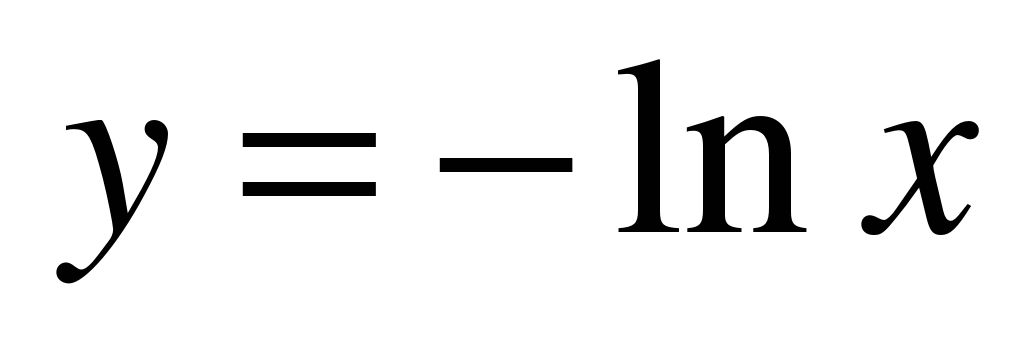 и осью Ox. и осью Ox. a) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной y. б) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. | Вариант 2. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2. Вычислить объем тела, образованного вращением относительно оси Ox плоской фигуры, ограниченной линиями 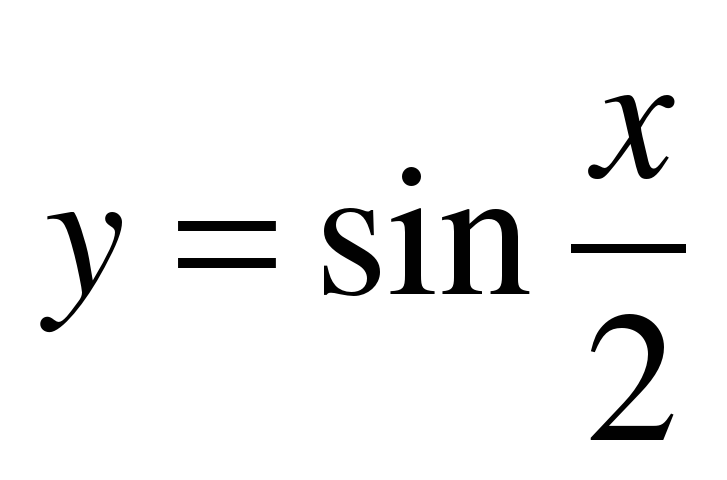 , , 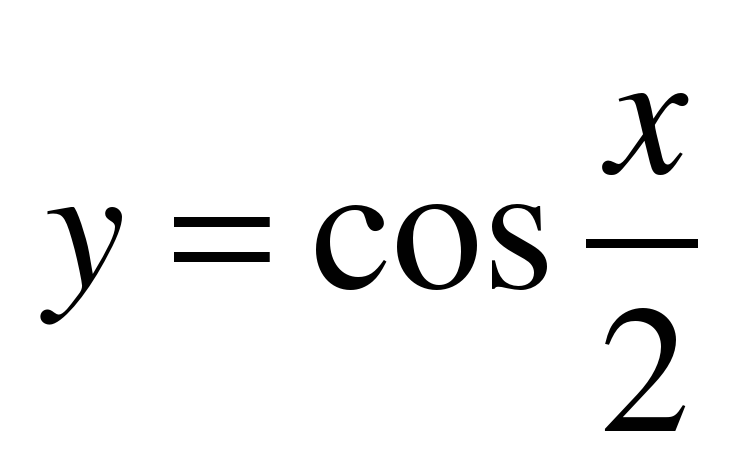 , где . , где . 3. Дана плоская фигура, ограниченная линиями , , . 1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. |
| Вариант 3. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2 Дана плоская фигура, ограниченная линиями , , . 1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. 3. Вычислить объем тела, образованного вращением относительно оси Ox плоской фигуры, ограниченной линиями 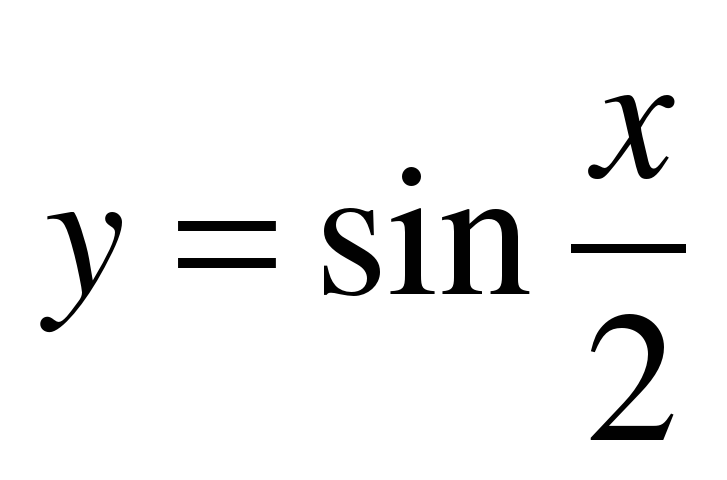 , , 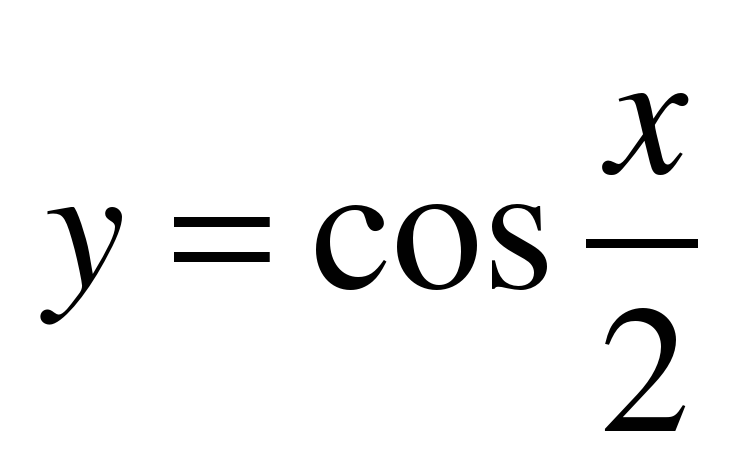 , где . , где . | Вариант 4. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2 Дана плоская фигура, ограниченная линиями , , . 3. Дана плоская фигура, ограниченная линиями x = 3, 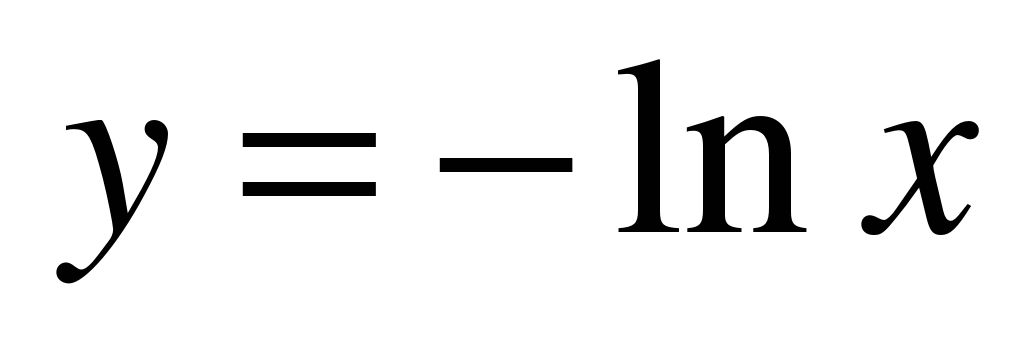 и осью Ox. и осью Ox. a) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной y. б) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. |
| Вариант5. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 2х – у – 2 = 0, у=0, х=7 3. Дана плоская фигура, ограниченная линиями x = 6, 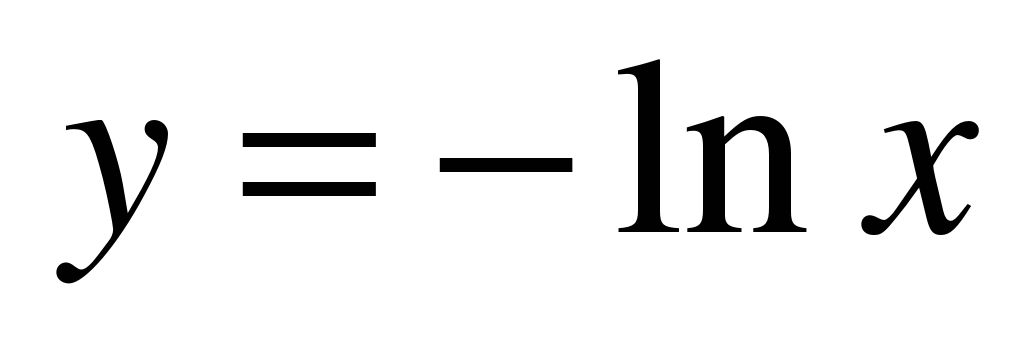 и осью Ox. и осью Ox. a) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной y. б) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу. | Вариант6. 1. Плоская фигура ограничена графиком параболы .Вычислить объем тела вращения. 2. Вычислить объем тела, образованного вращением относительно оси Ox плоской фигуры, ограниченной линиями 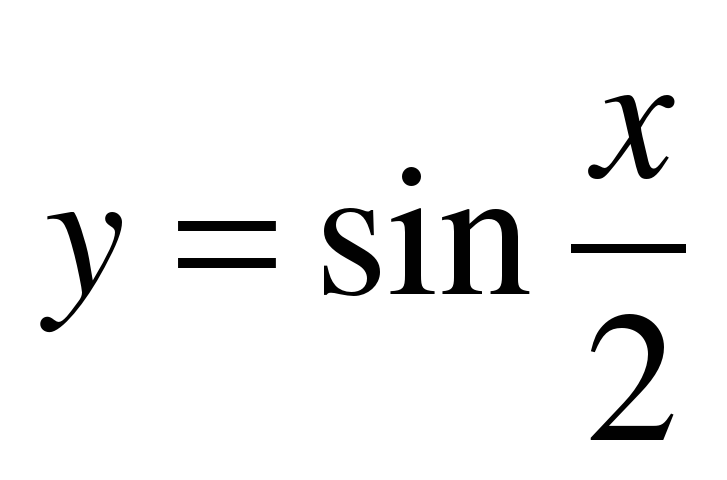 , , 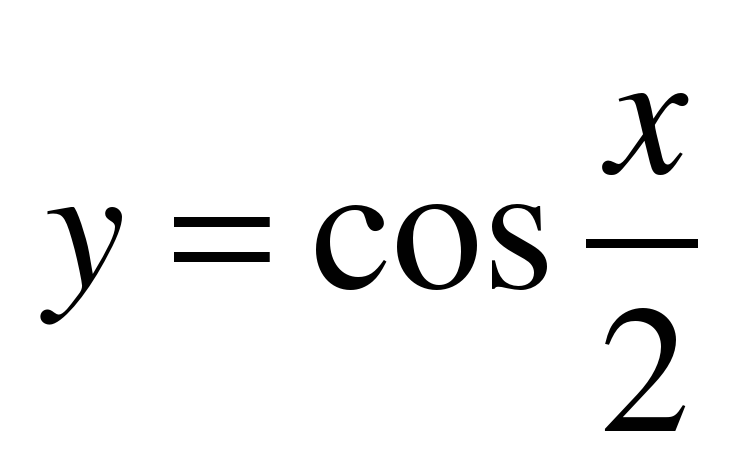 , где . , где . 2 Дана плоская фигура, ограниченная линиями , , . 1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси Оу.
|
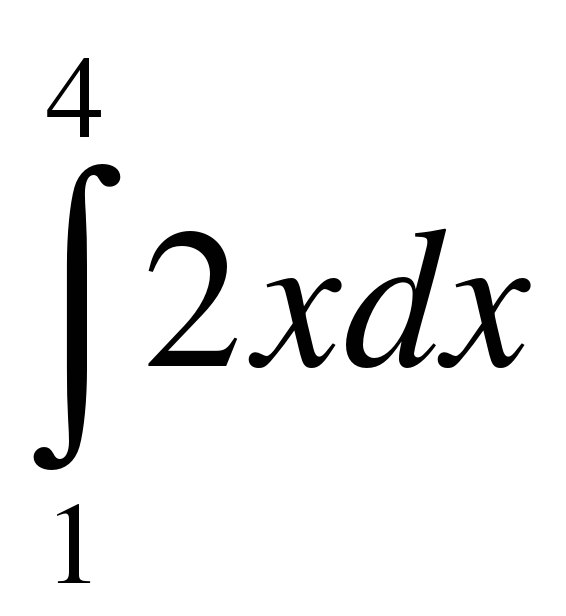
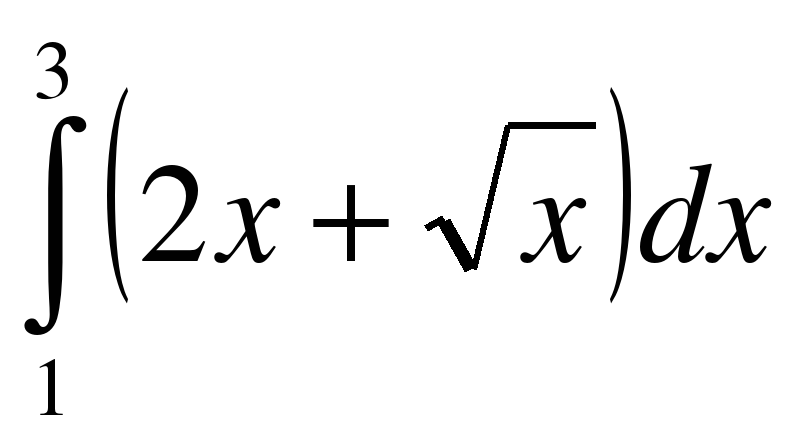
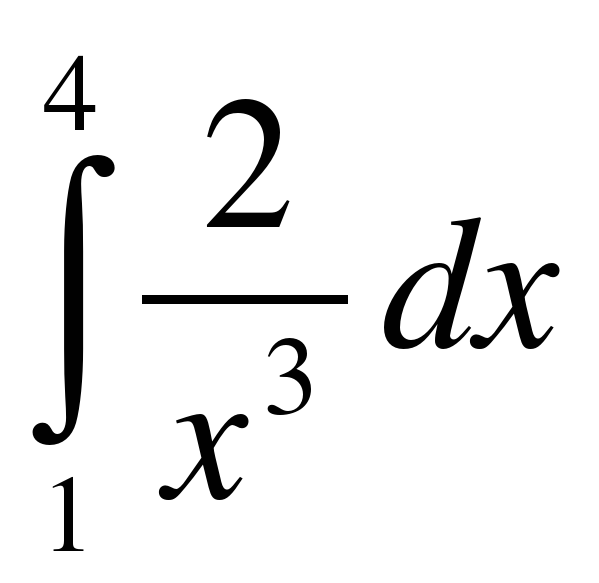
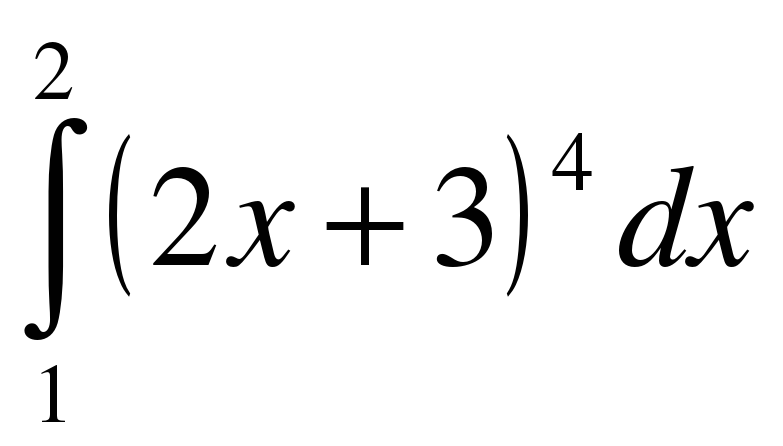
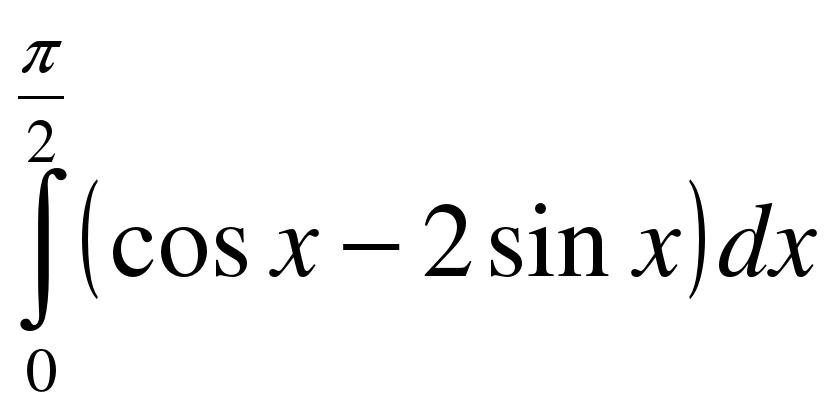

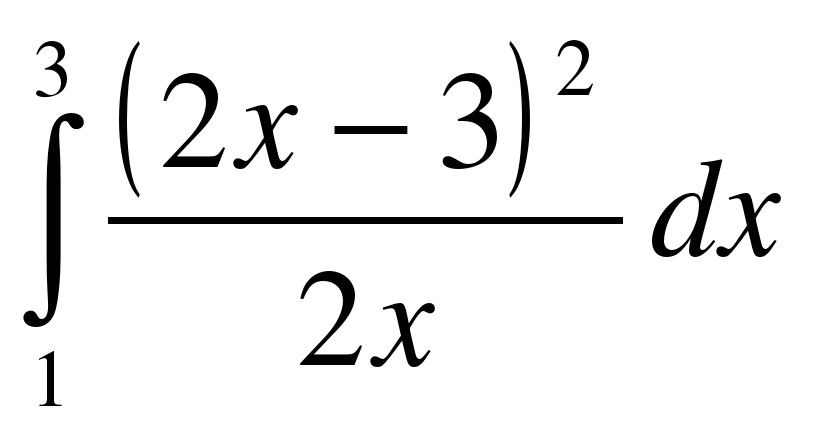 ;
;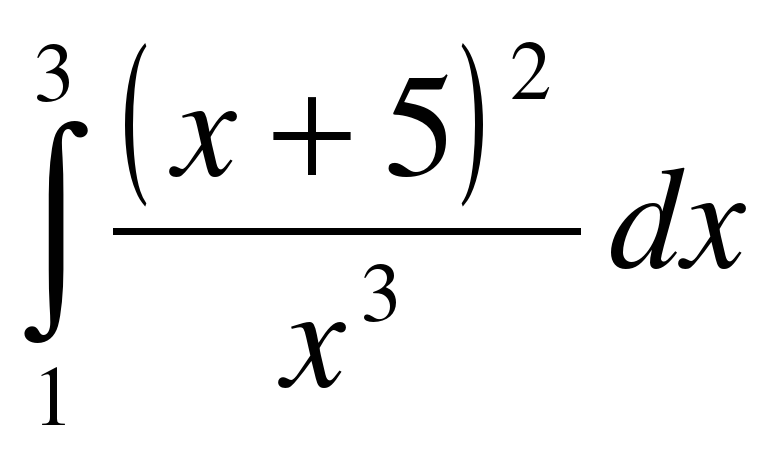 .
.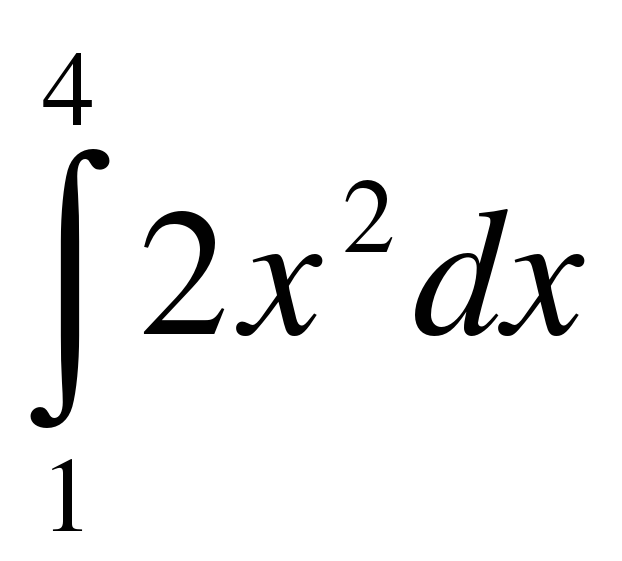
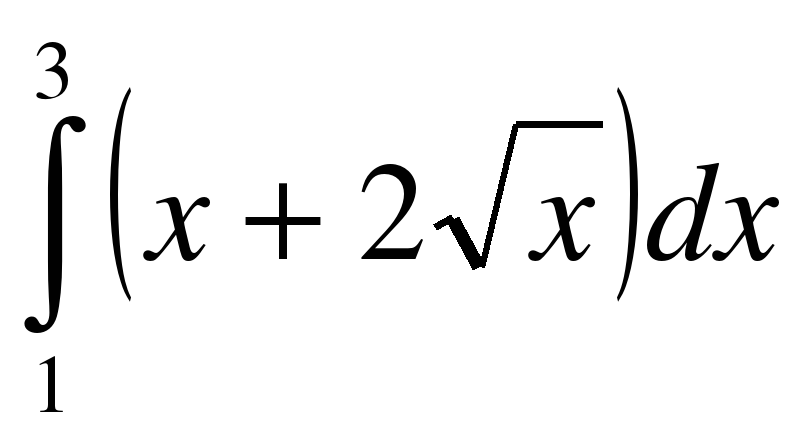
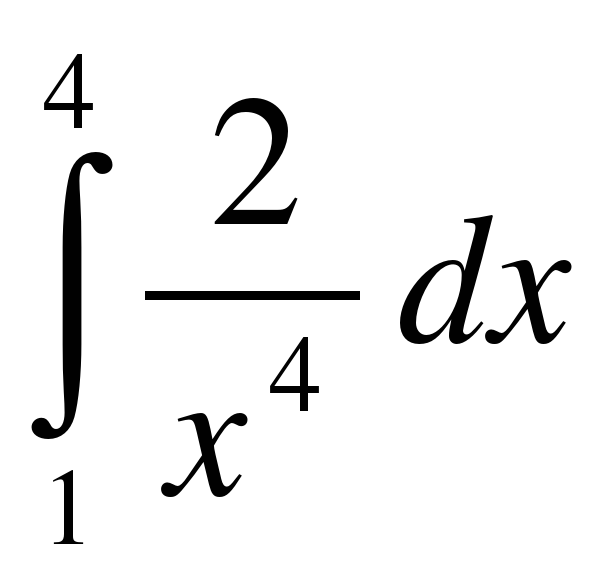
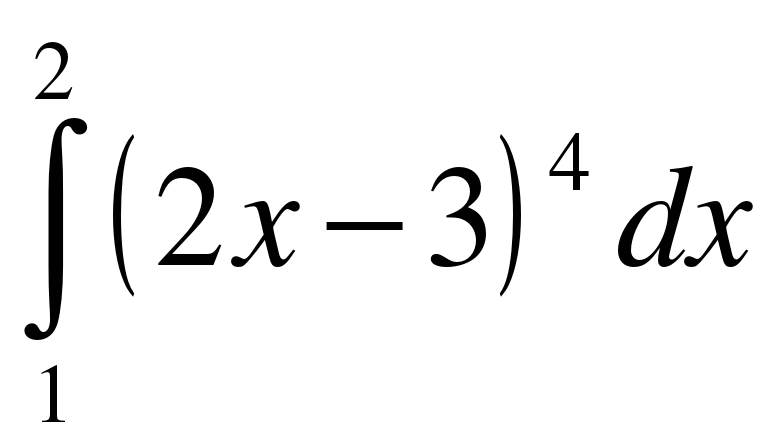
 ;
; .
.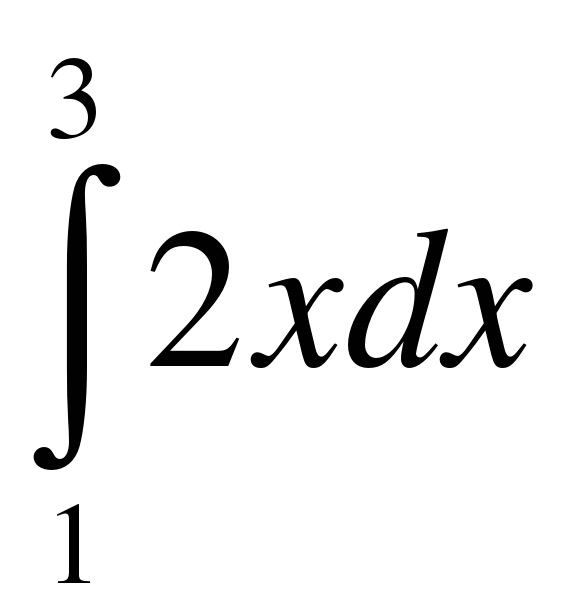
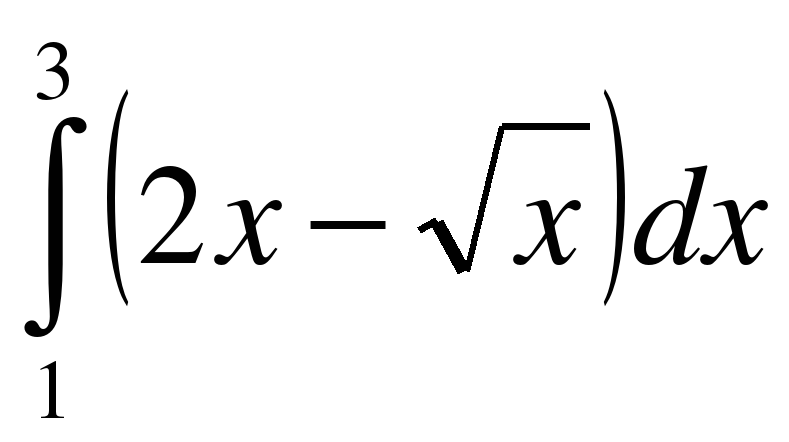
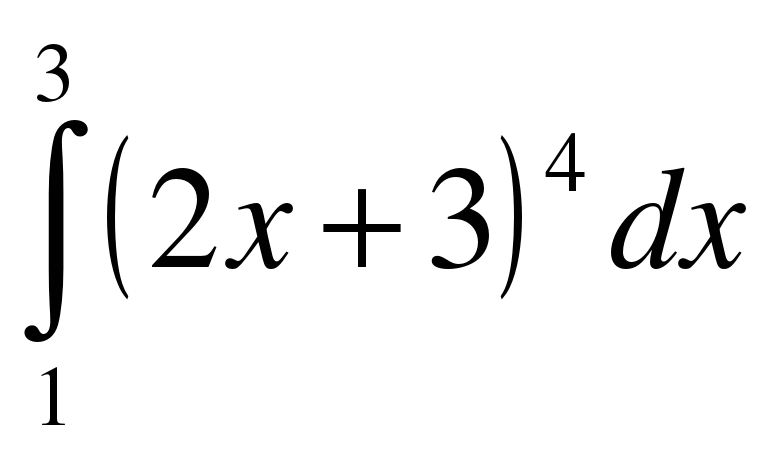
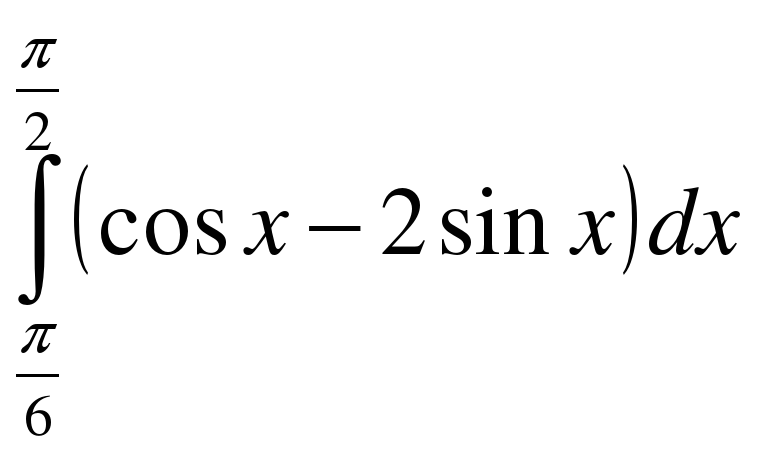
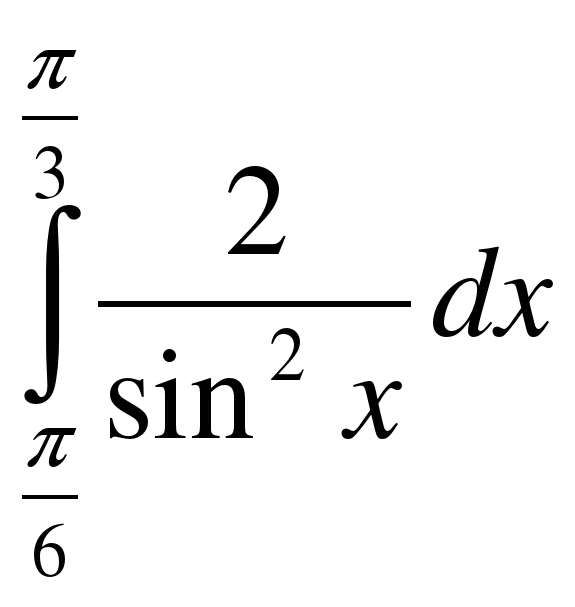
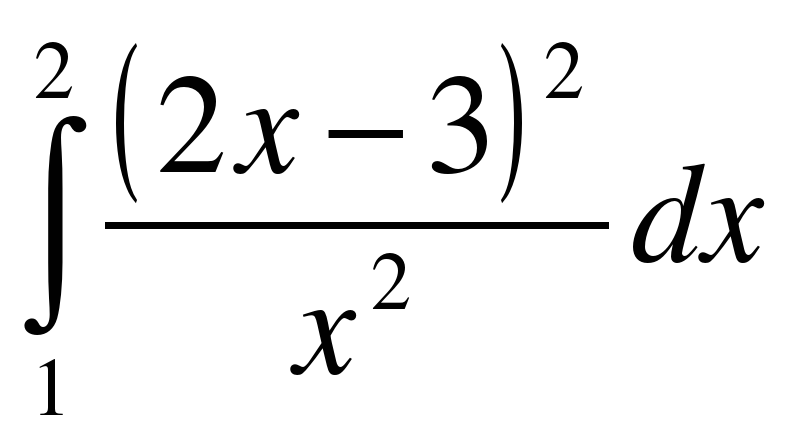 ;
;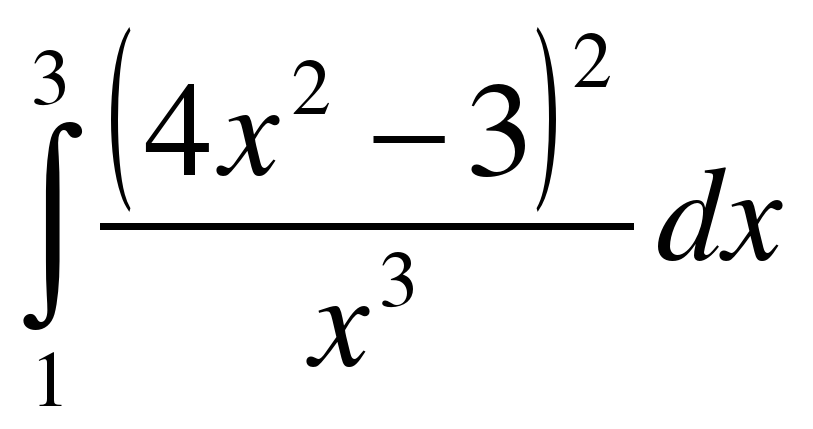 .
.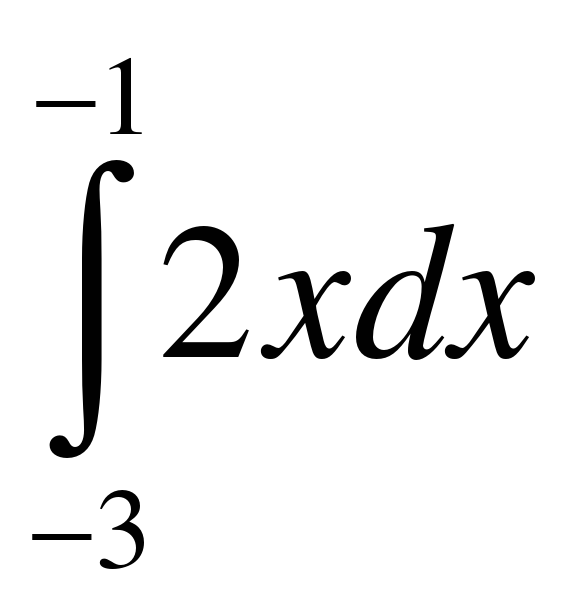
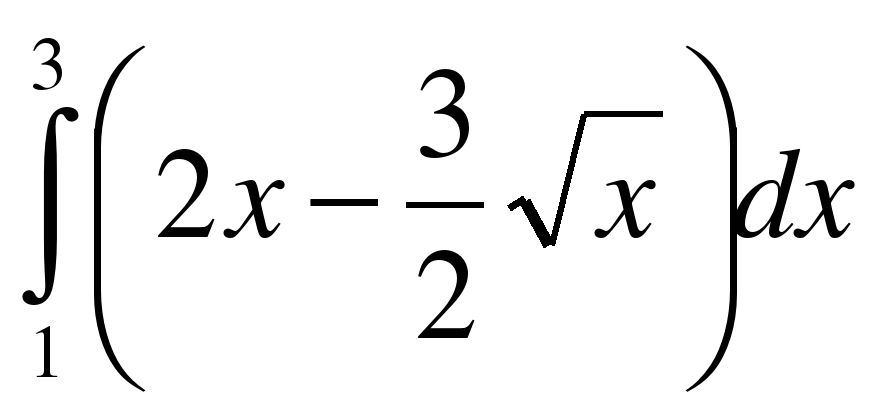


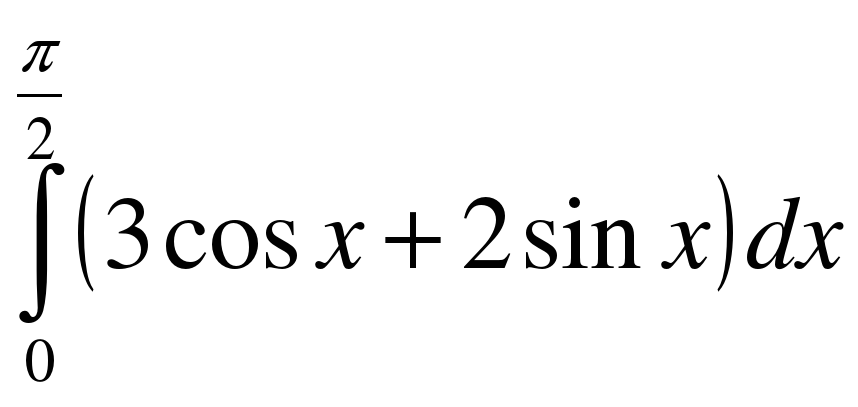
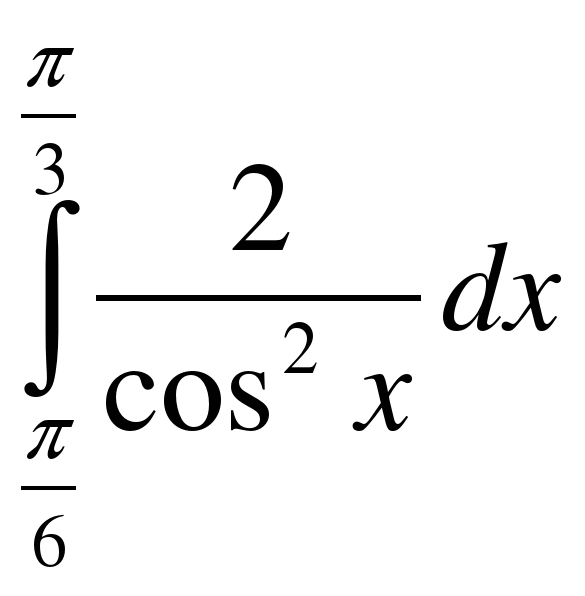
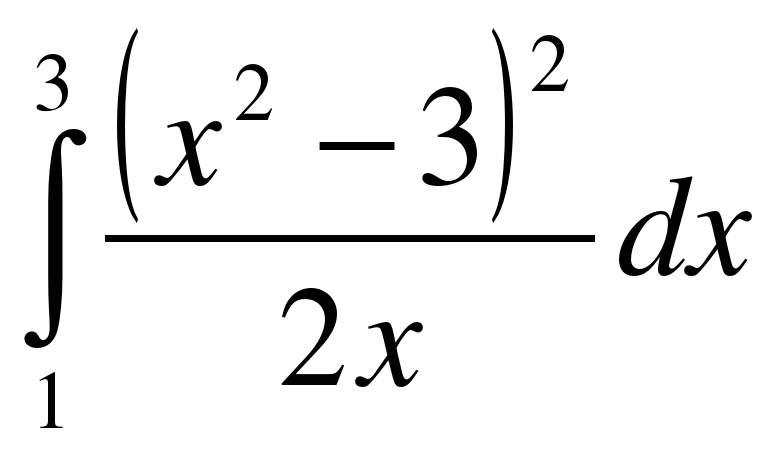 ;
;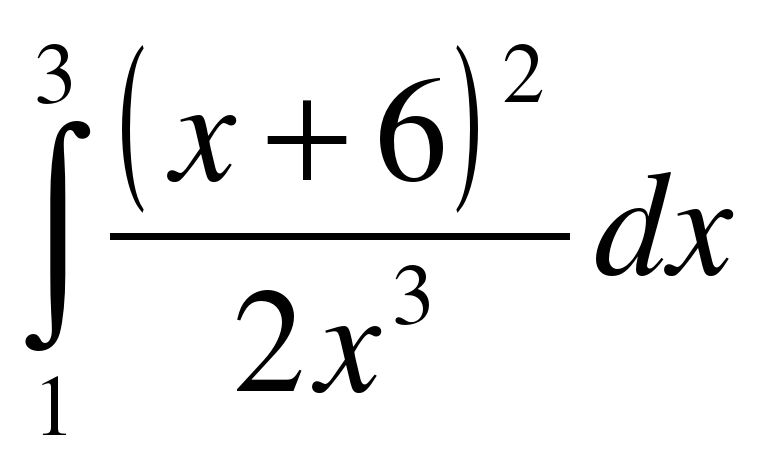 .
.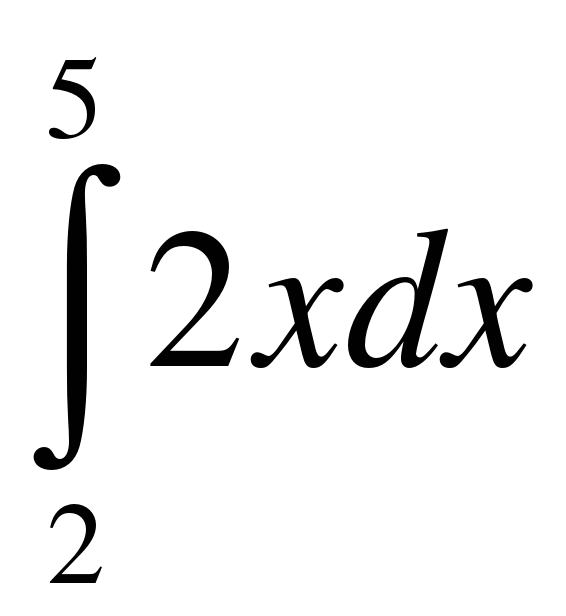
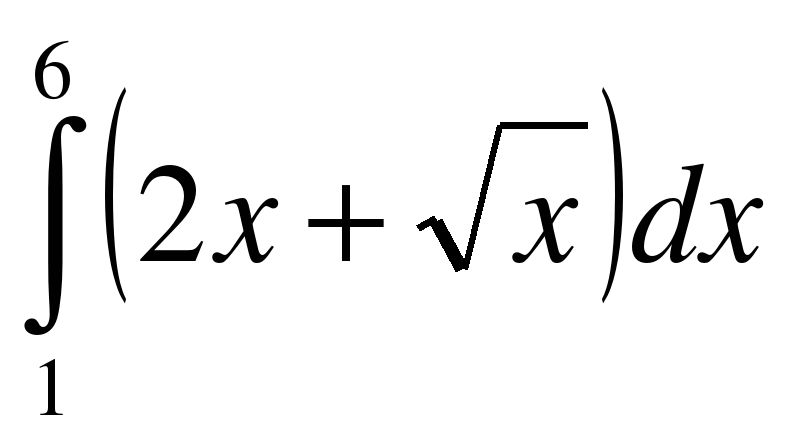
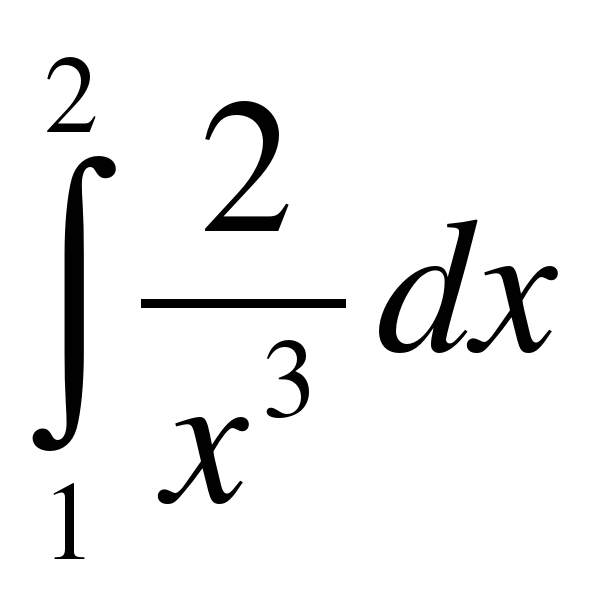
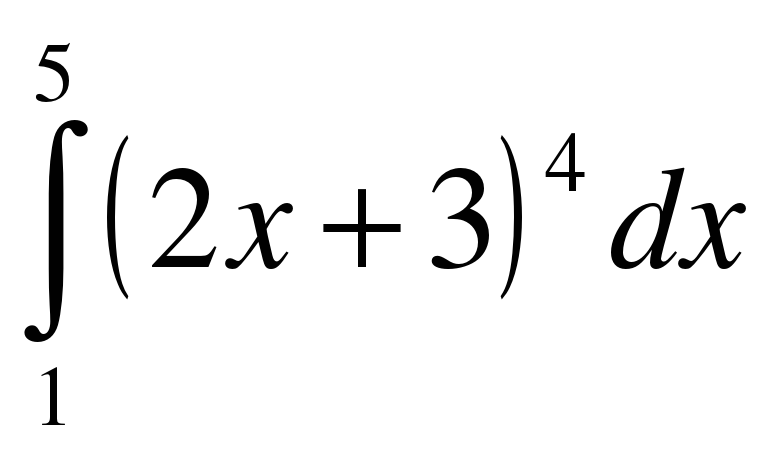
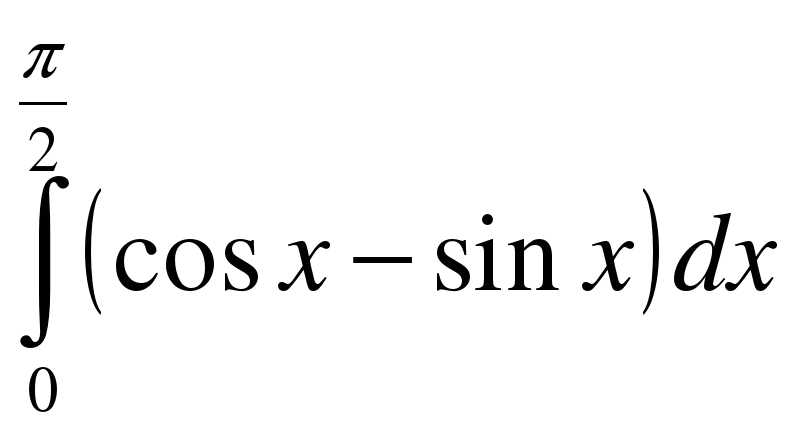
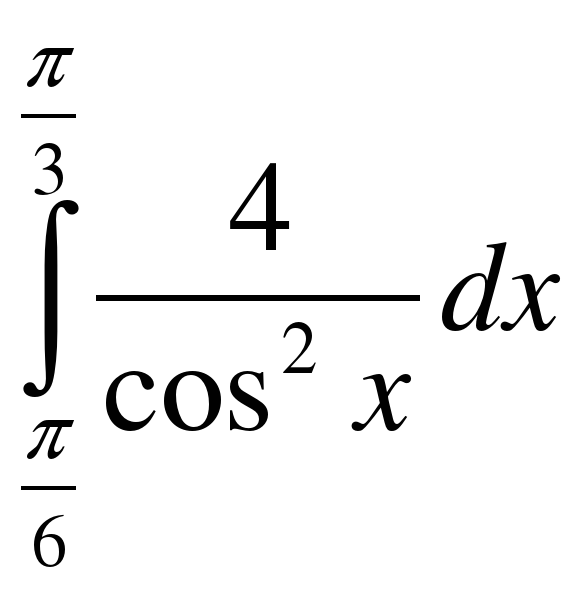
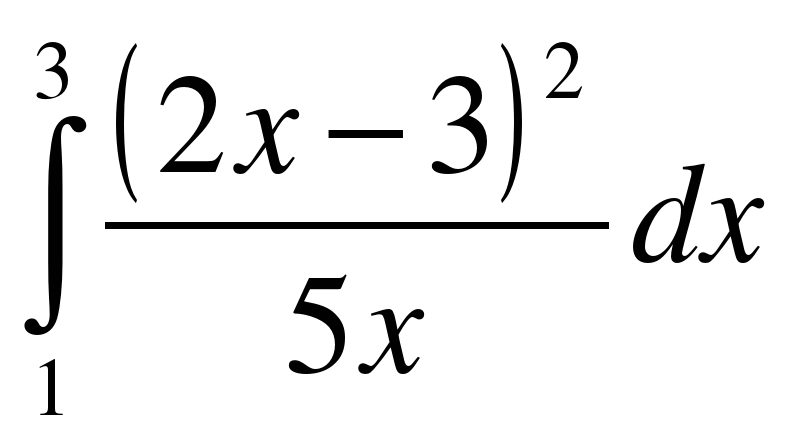 ;
;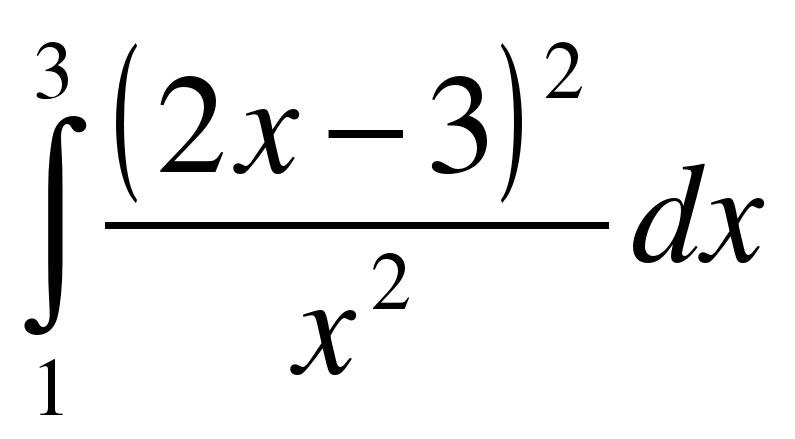 .
.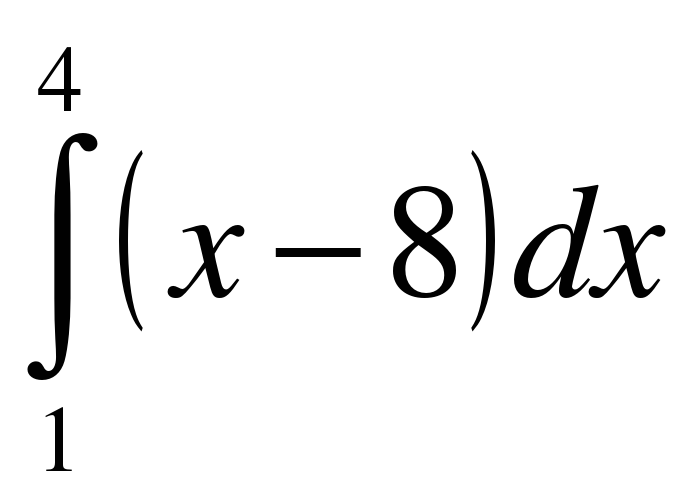
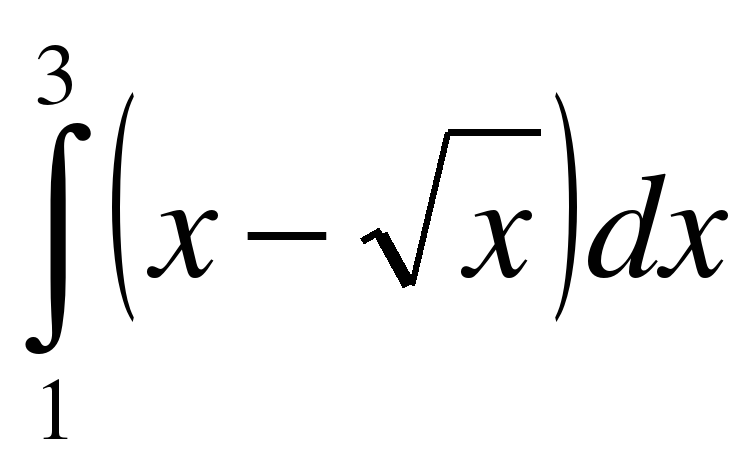
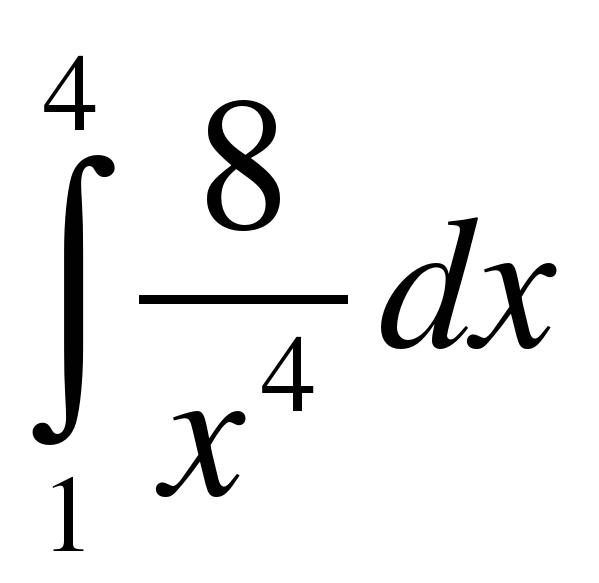
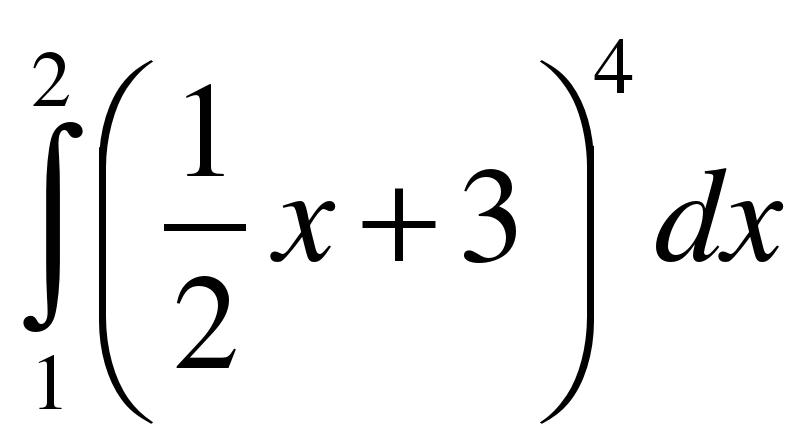
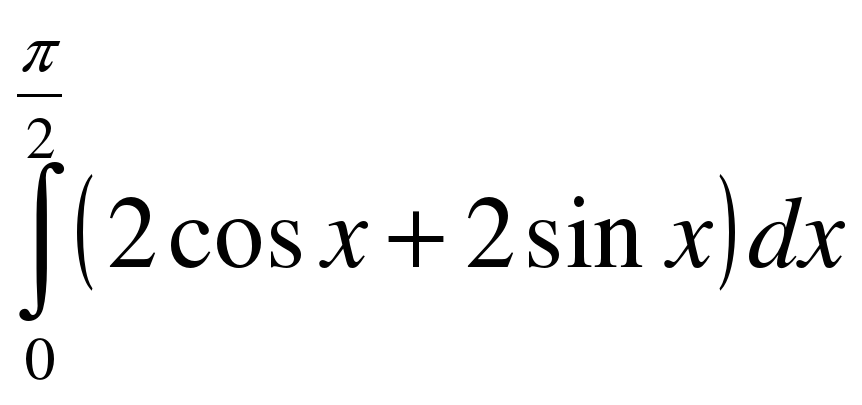
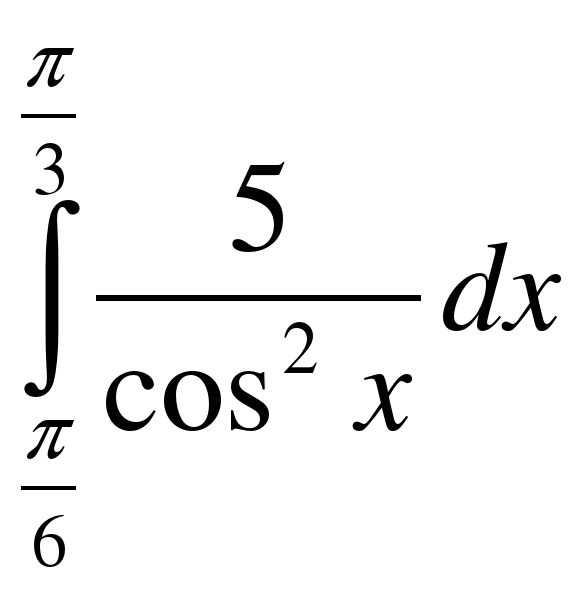
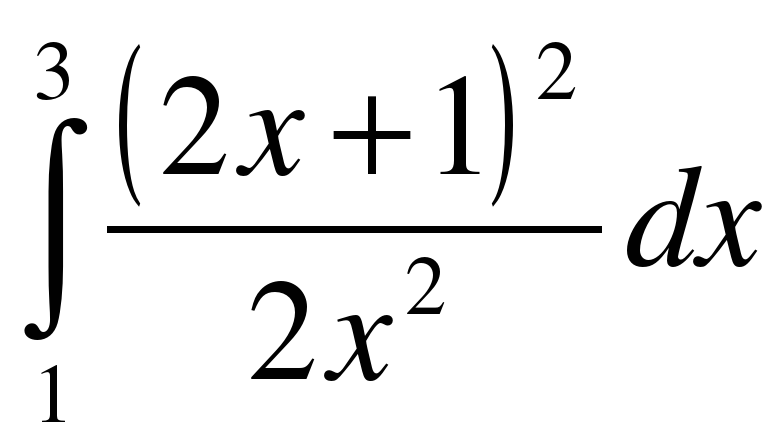 ;
;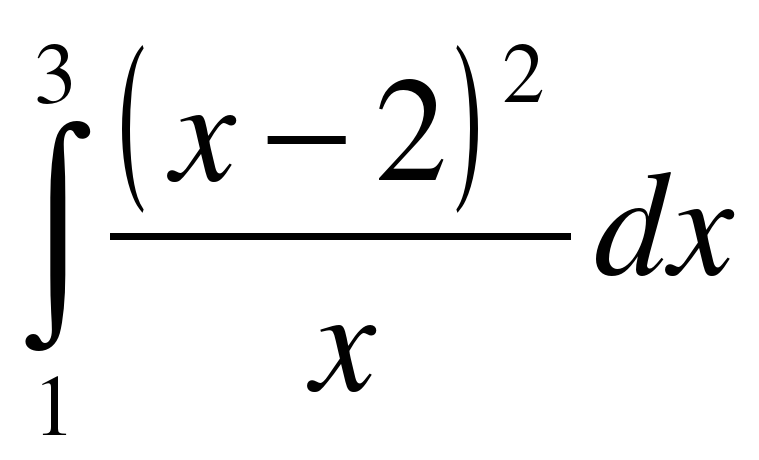 .
.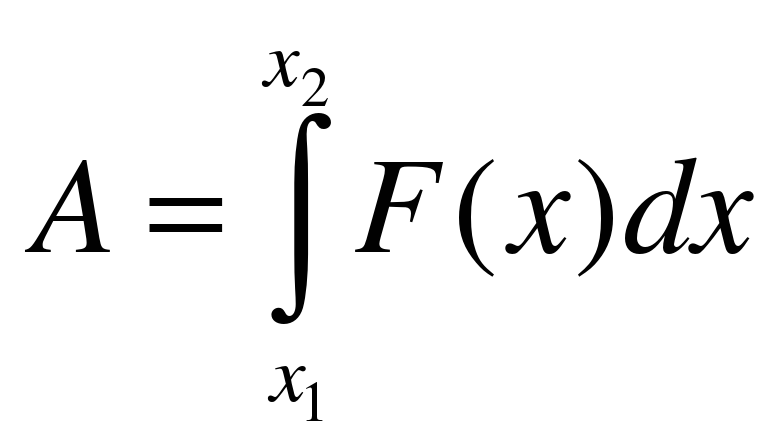 . Для нахождения
. Для нахождения 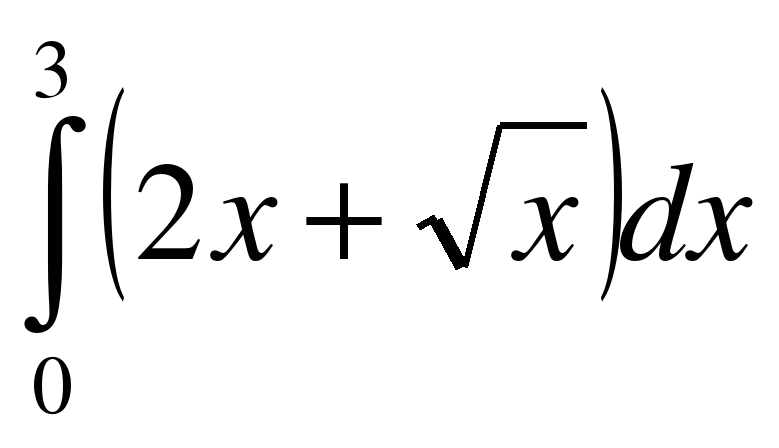 ;
;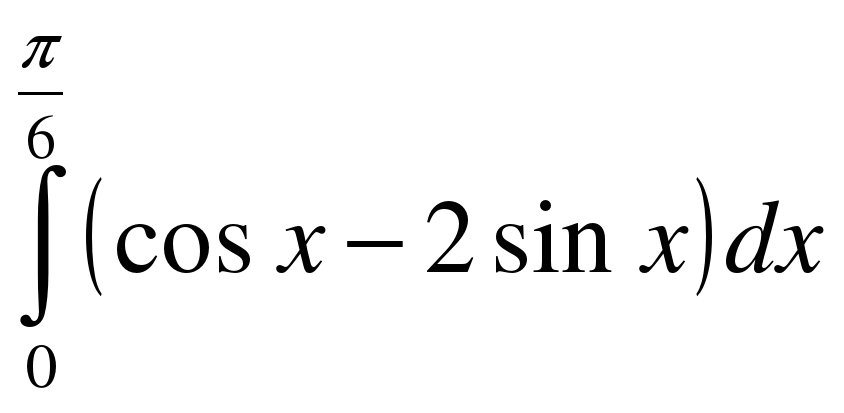 .
.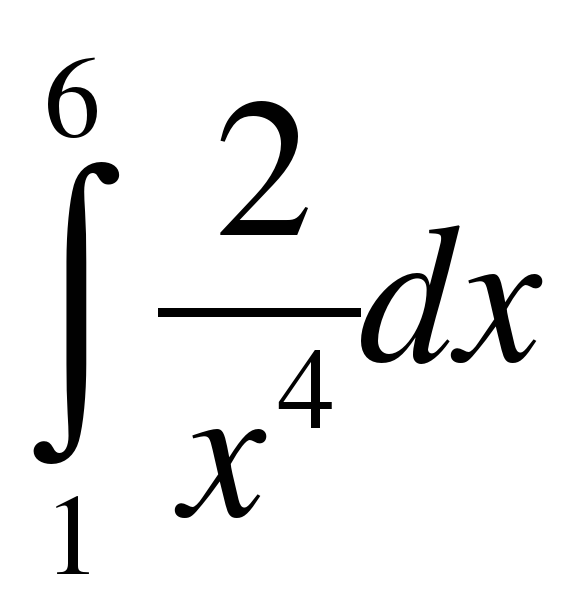 ;
;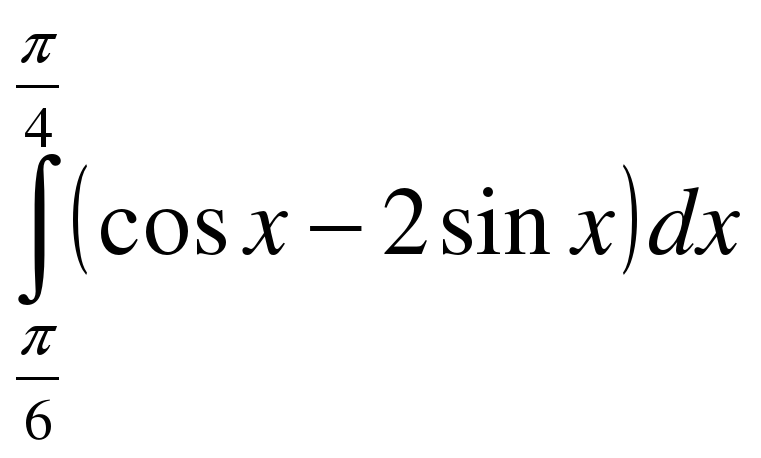 .
.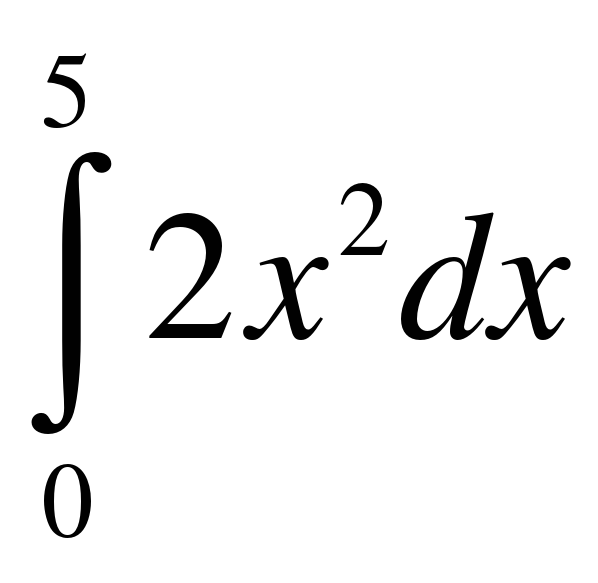 ;
;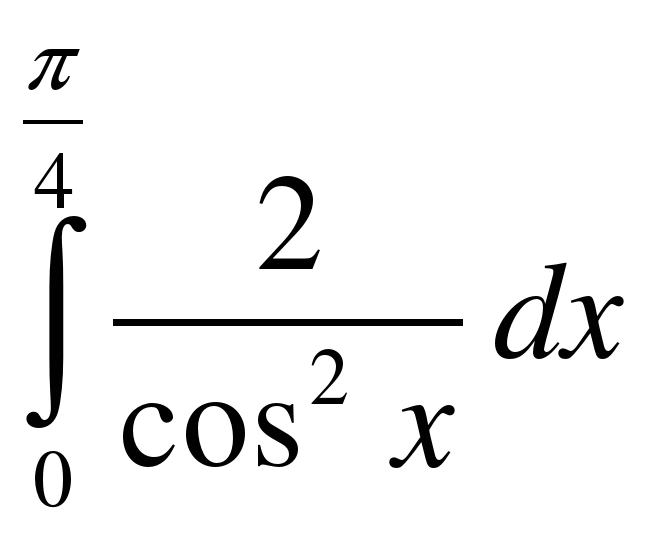 .
.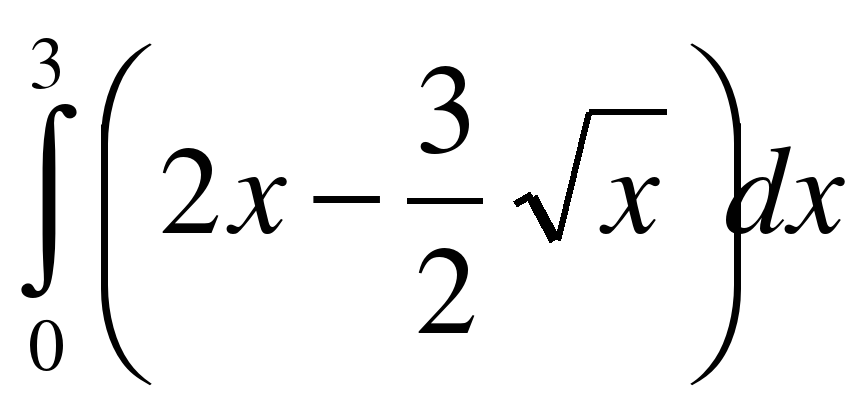 ;
;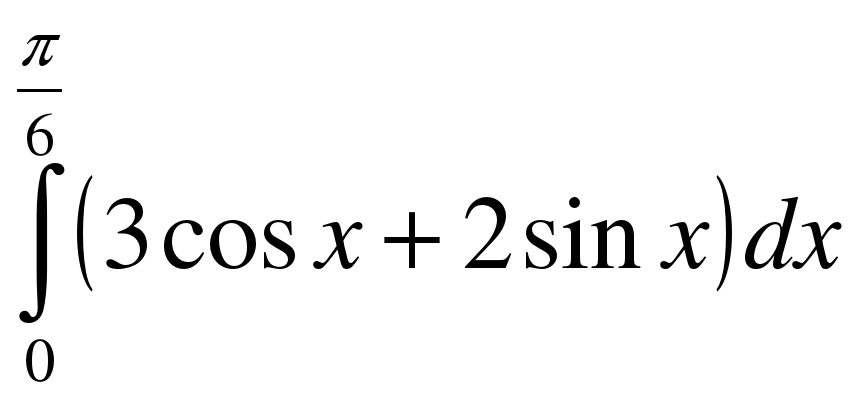 .
.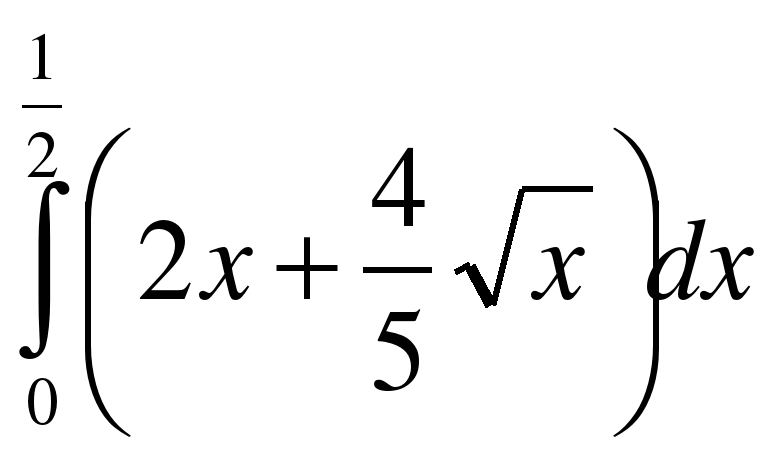 ;
;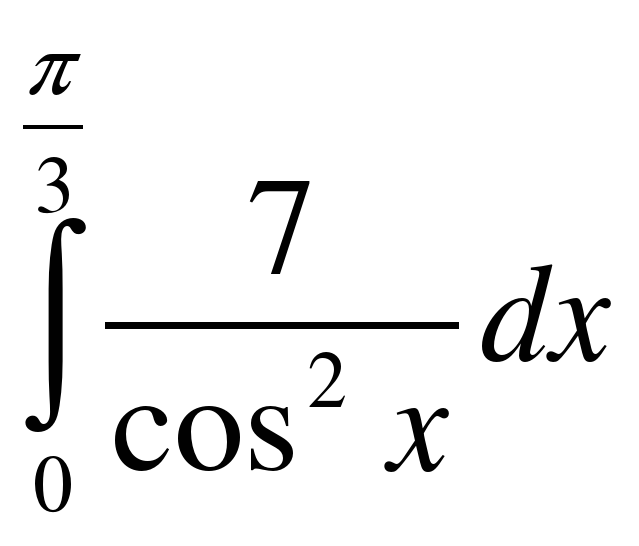 .
.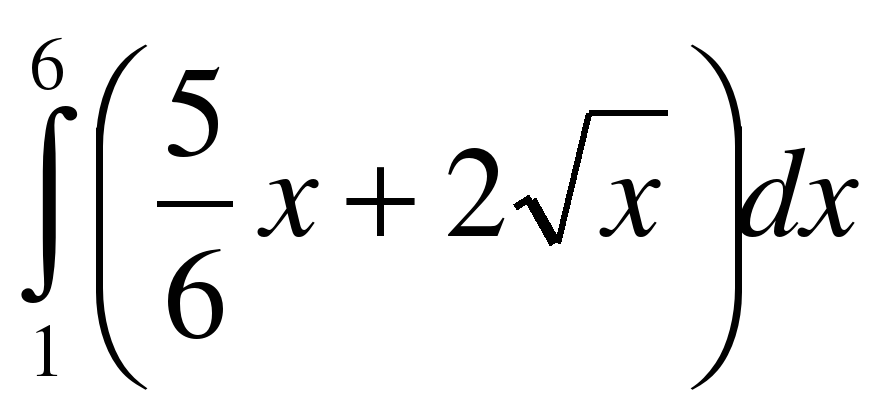 ;
;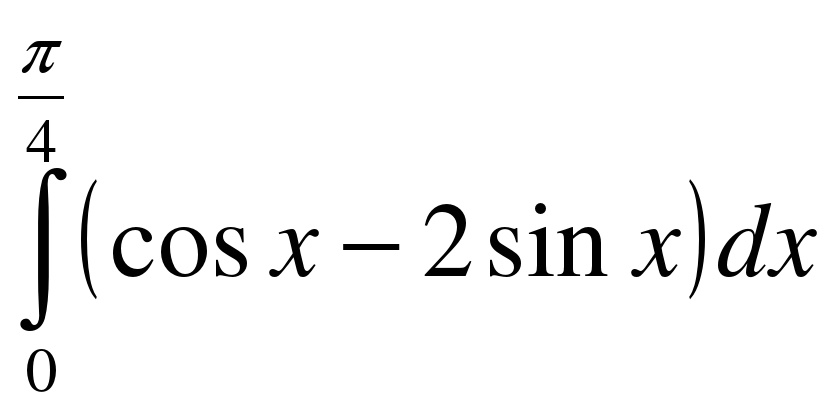 .
. ешение: Изобразим на чертеже плоскую фигуру, ограниченную линиями у = 2х + 1, у = х + 4, х = 0 и х = 1, не забывая при этом, что уравнение х = 0 задает ось Оу.
ешение: Изобразим на чертеже плоскую фигуру, ограниченную линиями у = 2х + 1, у = х + 4, х = 0 и х = 1, не забывая при этом, что уравнение х = 0 задает ось Оу.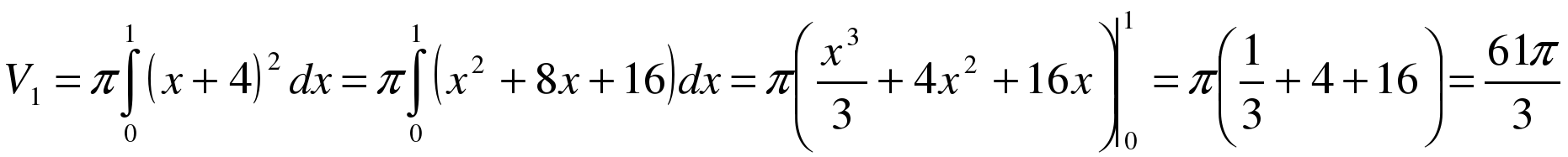 .
. .
. ешение:
ешение: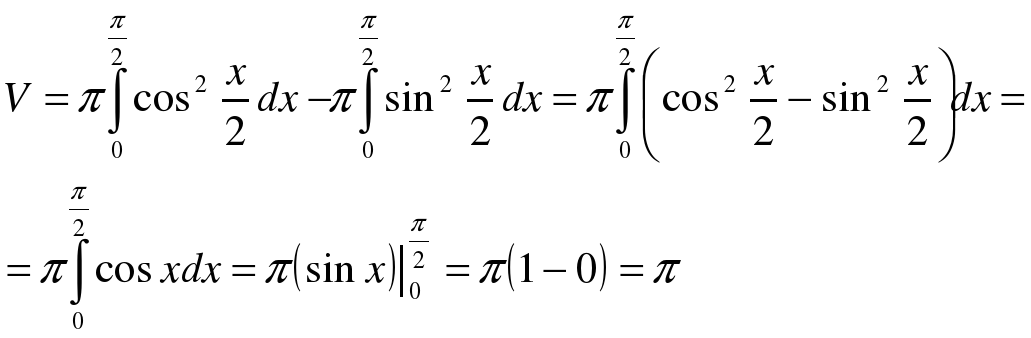
 ) Выполним чертёж:
) Выполним чертёж: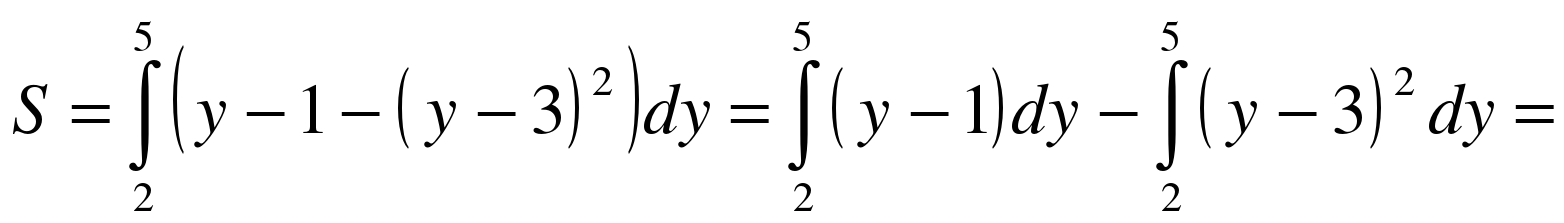

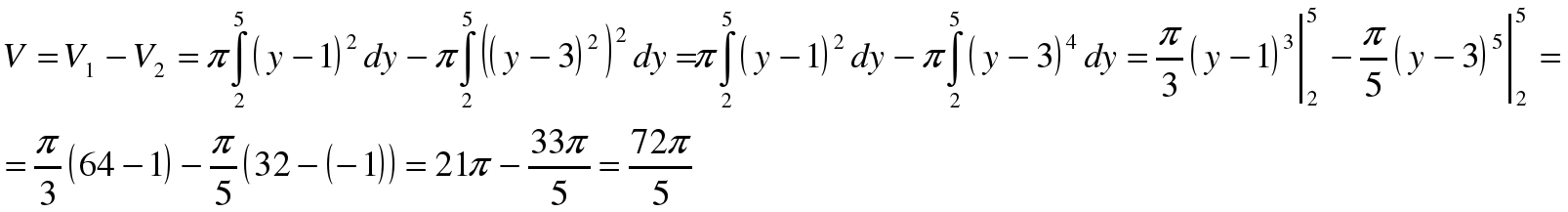
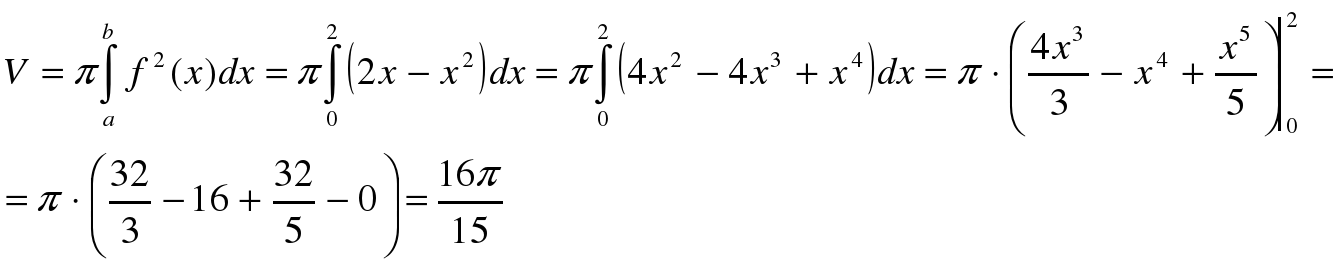
 .
.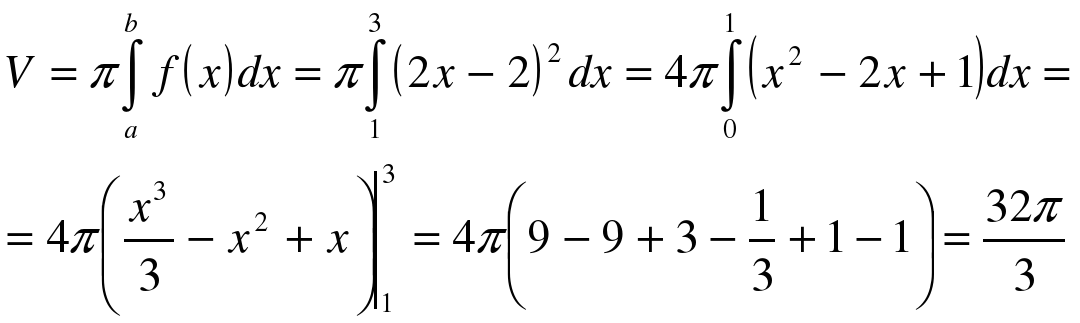
 ешение:
ешение: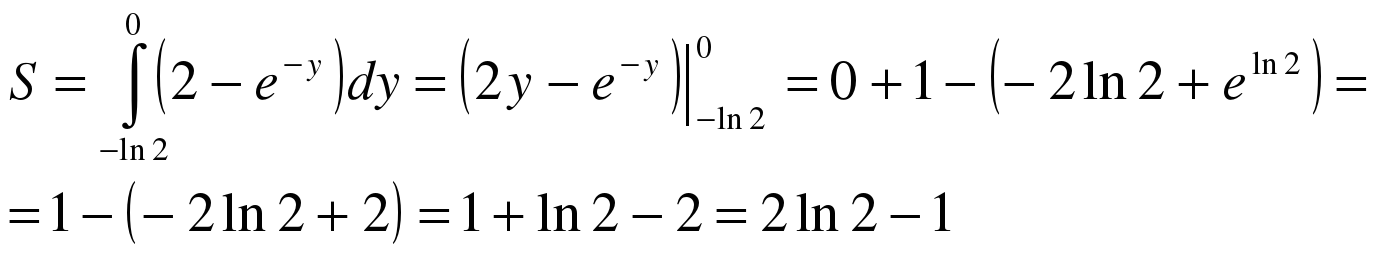
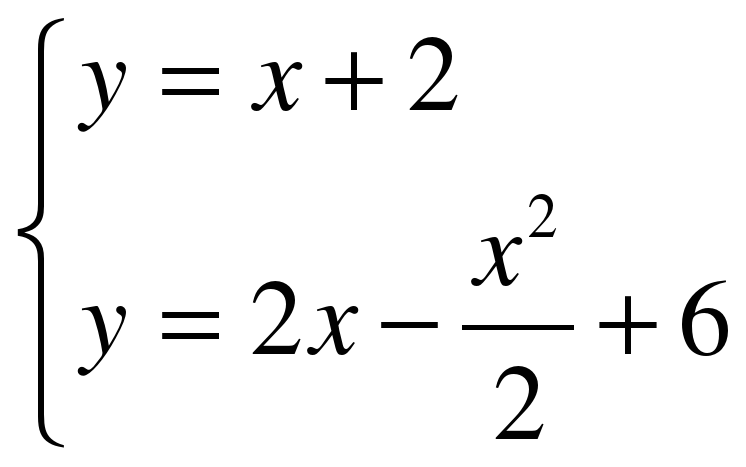
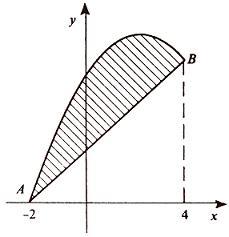 ля нахождения абсцисс точек пересечения заданных линий решаем уравнение:
ля нахождения абсцисс точек пересечения заданных линий решаем уравнение: 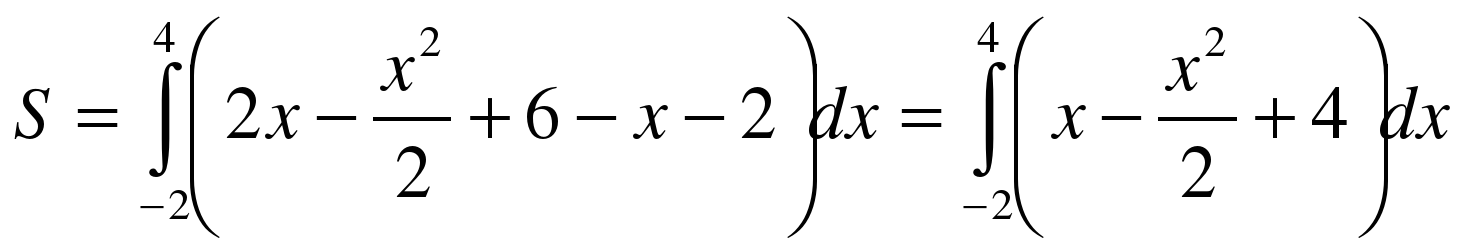 .
.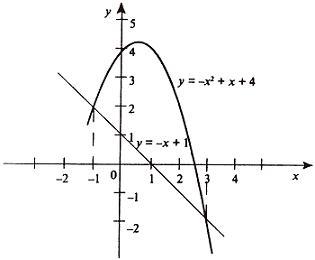 ример 2. Найти площадь фигуры, ограниченной линиями
ример 2. Найти площадь фигуры, ограниченной линиями 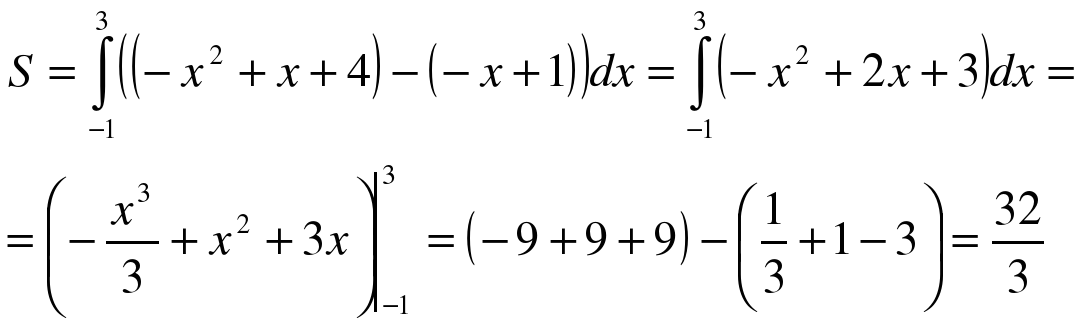
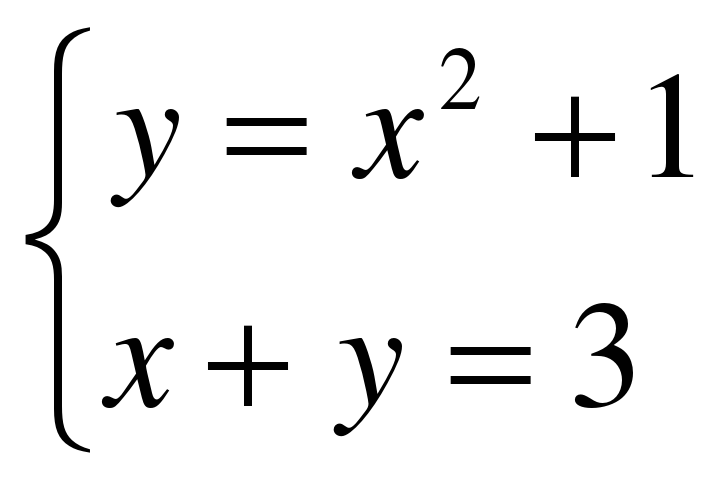 находим абсциссы точек пересечения x1 = – 2 и x2 = 1.
находим абсциссы точек пересечения x1 = – 2 и x2 = 1.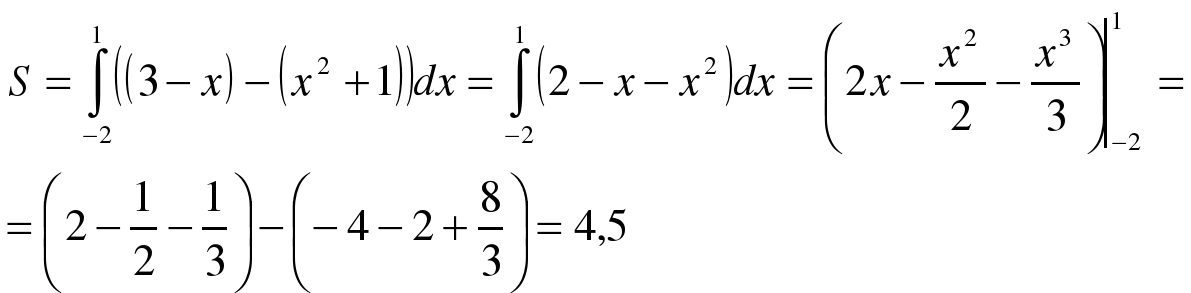
 ешение.
ешение.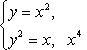
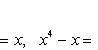
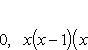
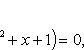

 ешение.
ешение.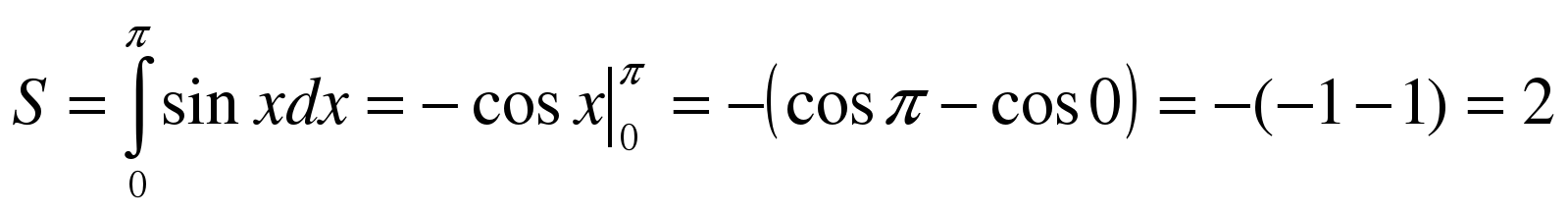 .
.
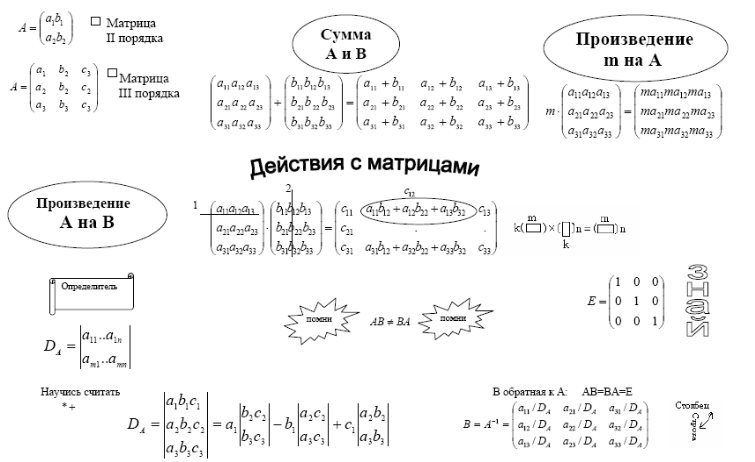
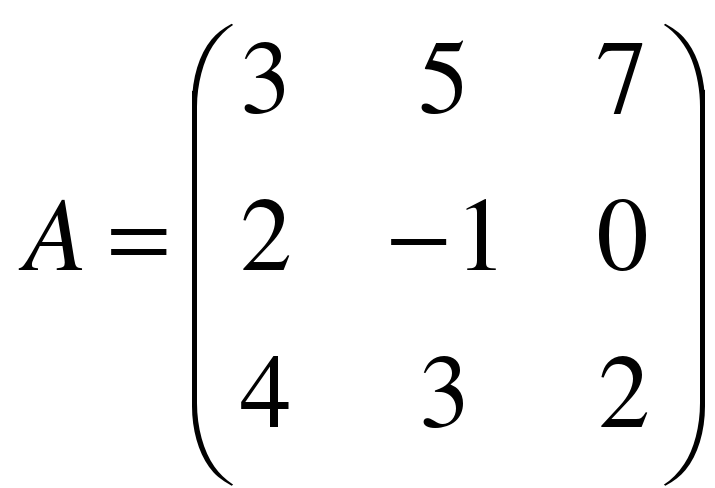 ,
, 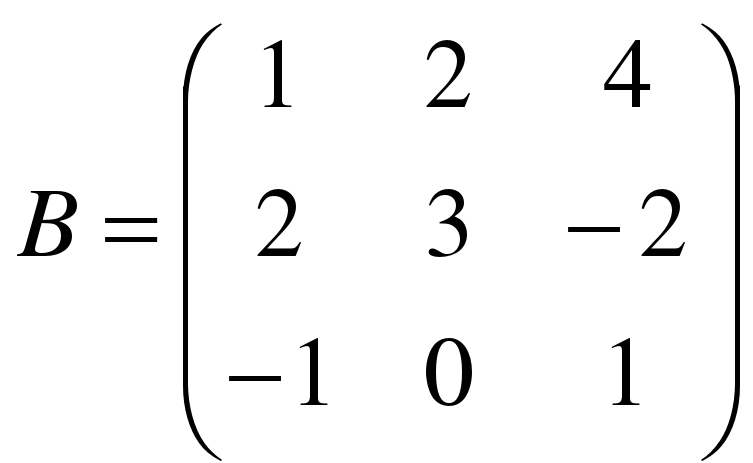 .
.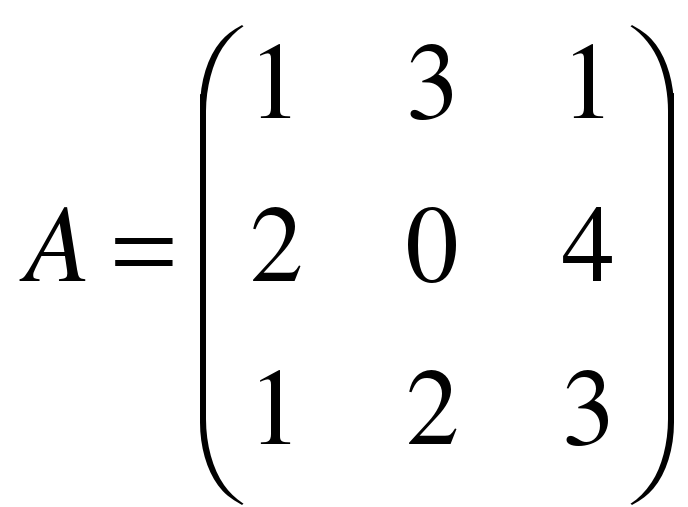 ,
, 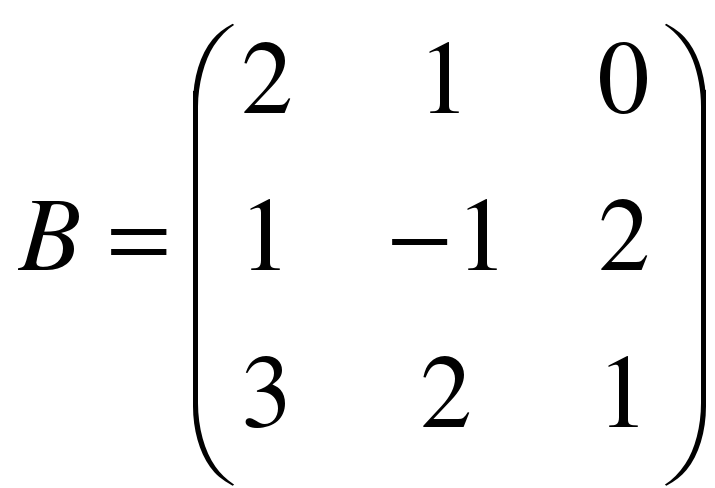 .
.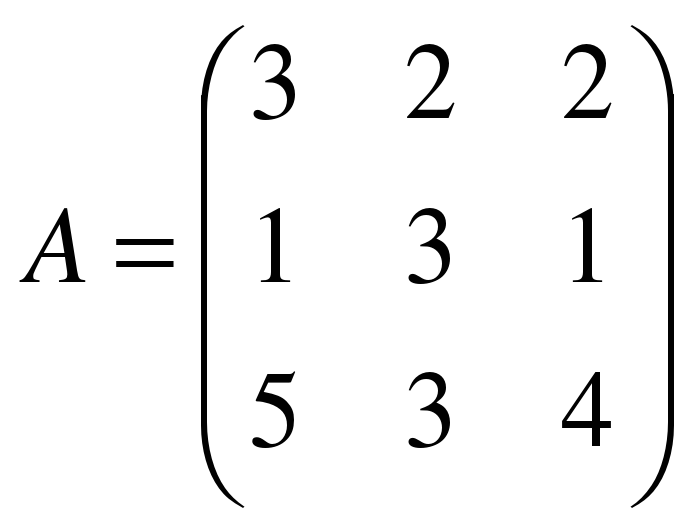 , сделать проверку.
, сделать проверку.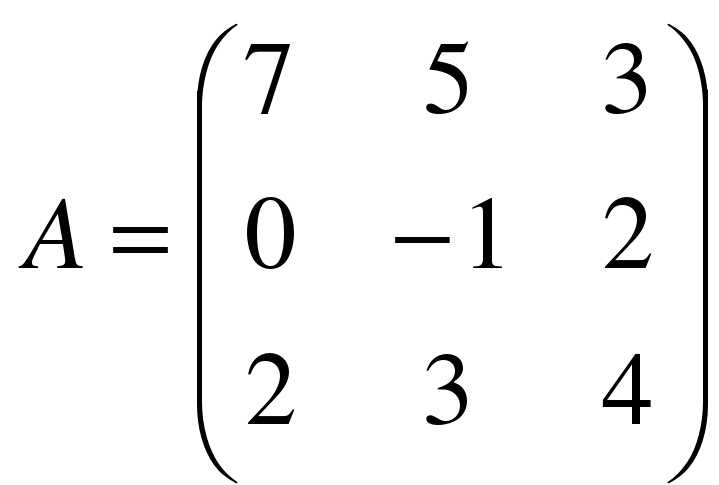 ,
, 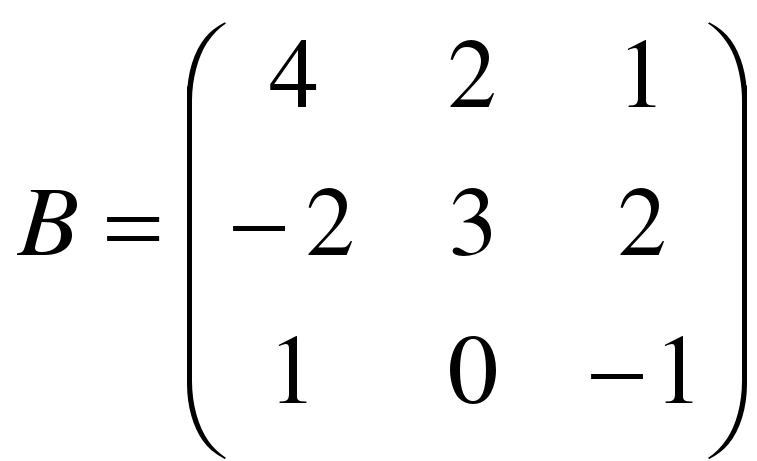 .
.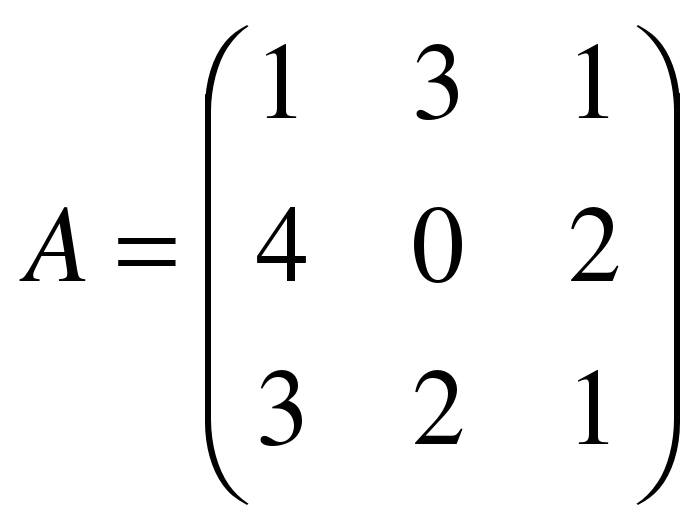 ,
, 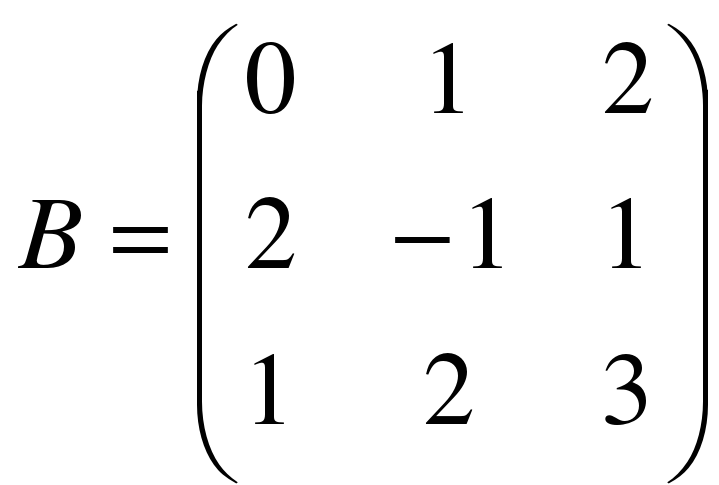 .
.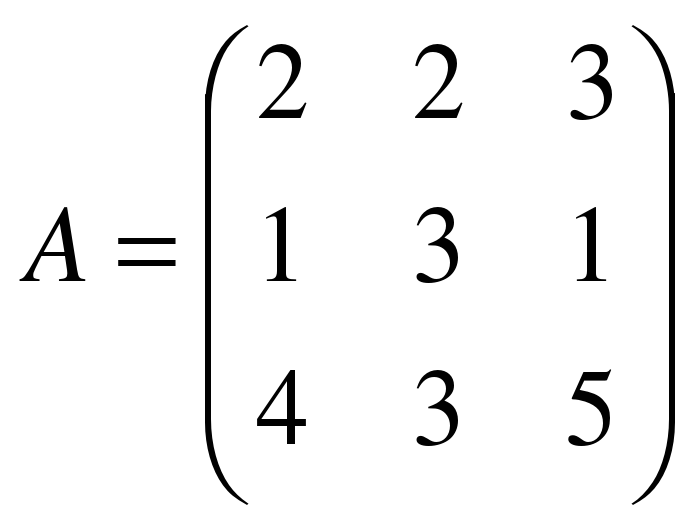 , сделать проверку.
, сделать проверку.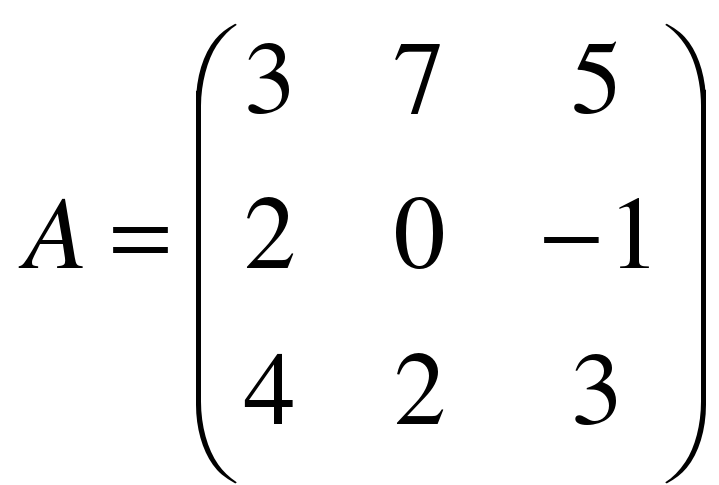 ,
, 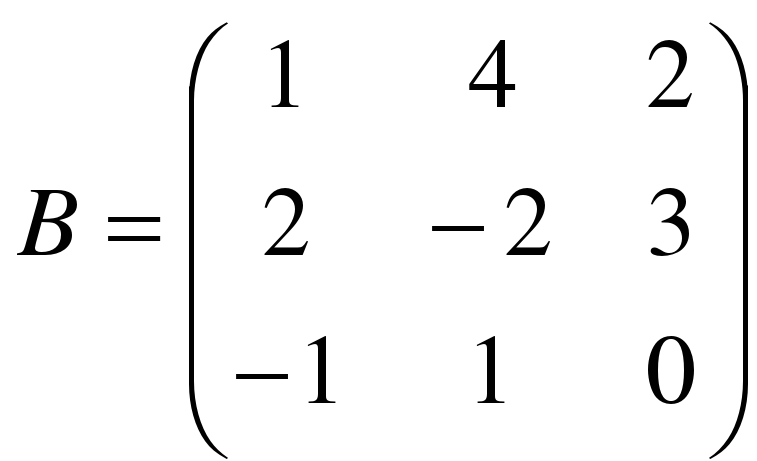 .
. ,
, 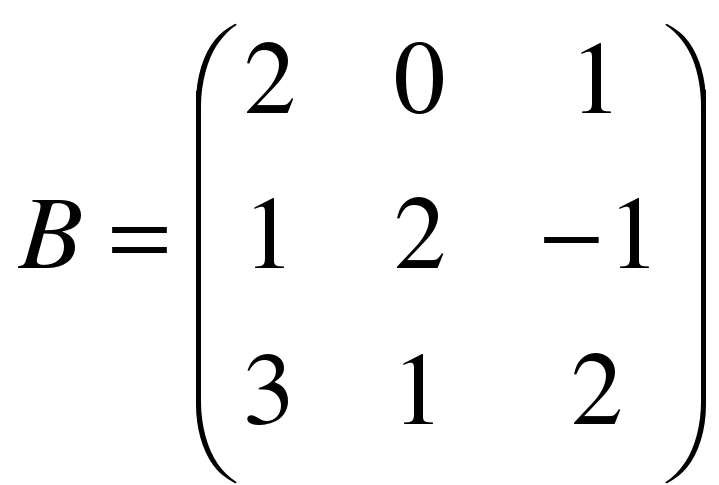 .
.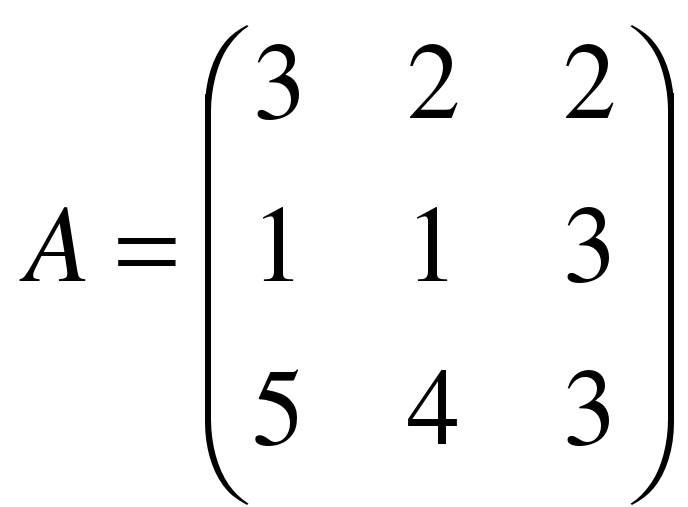 , сделать проверку.
, сделать проверку. ,
, 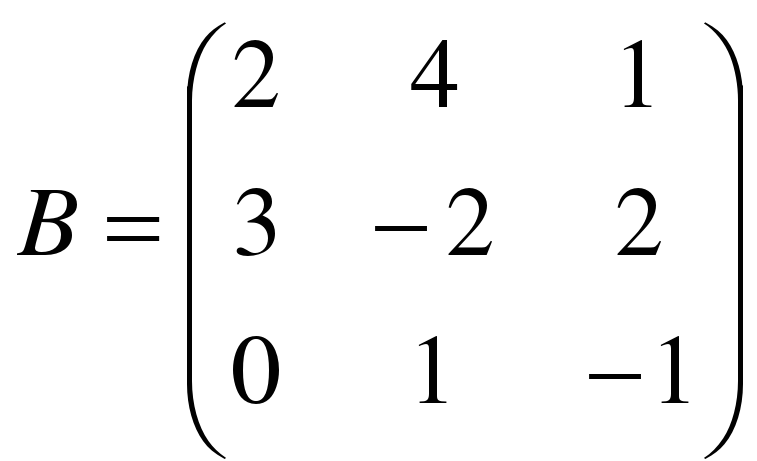 .
. ,
, 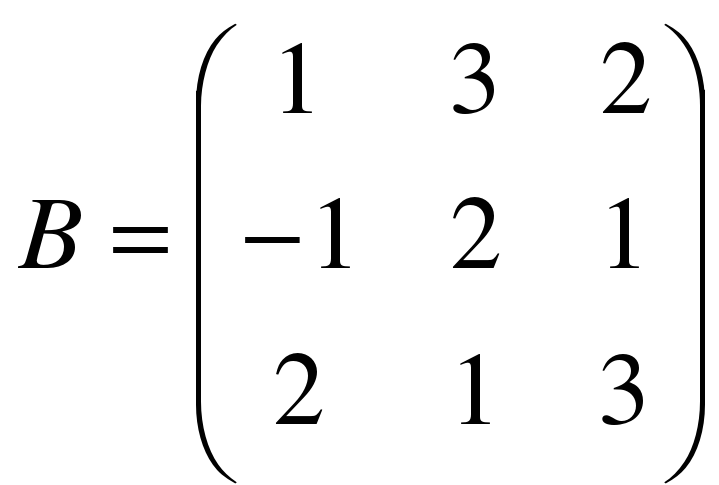 .
. , сделать проверку.
, сделать проверку.















