Если, решая проблему, ученик самостоятельно отыскивает выход из сложной ситуации, то он действительно думает. Поэтому в жизни он сможет отстоять свою точку зрения. Урок одной задачи способствует развитию критического мышления и развивает индивидуальные способности ученика.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Практический кейс для 9-11 класса: "Урок одной задачи".
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Практический кейс для 9-11 класса: "Урок одной задачи".»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1900 руб.
3170 руб.
1900 руб.
3170 руб.
1690 руб.
2820 руб.
1910 руб.
3190 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

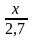 =
=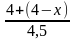
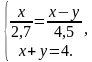


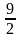 =
= 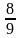 (ч)-время, которое затратил второй на путь А О;
(ч)-время, которое затратил второй на путь А О;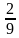 (ч)-время каждого;
(ч)-время каждого;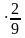 = 0,6(км) –длина пути СВ;
= 0,6(км) –длина пути СВ;


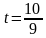
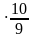 =3 (км).
=3 (км). 





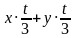 (во втором случае). Получим уравнение: уt-хt =
(во втором случае). Получим уравнение: уt-хt =















