Методические указания по решению однородных тригонометрических уравнений первой и второй степени: данные указания адресованы в первую очередь учащимся 10 и 11 классов для подготовки к экзамену по математике. так же может быть использовано учителями математики для подготовки к урокам по данной теме. В указаниях особое внимание уделяется вопросу о потере корней при делении уравнений на функцию, так как этот немаловажный вопрос в школьных учебниках не освещается в полном объеме.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Однородные тригонометрические уравнения
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Однородные тригонометрические уравнения »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1910 руб.
3190 руб.
1540 руб.
2560 руб.
1730 руб.
2880 руб.
1720 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
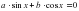 , где
, где 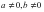 , называется однородным тригонометрическим уравнением первой степени. Для его решения достаточно обе части уравнения разделить на cosx:
, называется однородным тригонометрическим уравнением первой степени. Для его решения достаточно обе части уравнения разделить на cosx: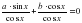 , учитывая, что
, учитывая, что 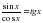 , получаем:
, получаем: 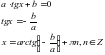
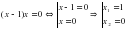
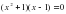 двумя способами.
двумя способами.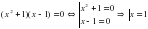
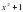 , получим
, получим 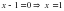
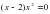 двумя способами
двумя способами 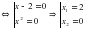
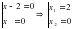
 ,
,

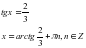
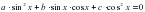 , где
, где 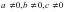 ,называется однородным тригонометрическим уравнением второй степени. Для его решения достаточно
,называется однородным тригонометрическим уравнением второй степени. Для его решения достаточно  обе части уравнения разделить на
обе части уравнения разделить на  :
: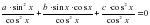 ,
, 
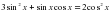
 . Получили однородное тригонометрическое уравнение второй степени. Разделим уравнение на
. Получили однородное тригонометрическое уравнение второй степени. Разделим уравнение на 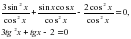
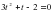 Корнями этого уравнения являются:
Корнями этого уравнения являются: 
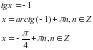


 получим:
получим: . Получили однородное тригонометрическое уравнение второй степени. Разделим уравнение на
. Получили однородное тригонометрическое уравнение второй степени. Разделим уравнение на 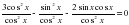
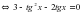 . Пусть
. Пусть 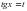 , получаем квадратное уравнение:
, получаем квадратное уравнение: 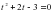 . Корни этого уравнения:
. Корни этого уравнения: 
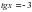

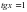
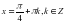
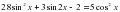
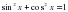 , получаем:
, получаем:















