КОМБИНАТОРИКА, ТЕОРИЯ ВЕРОЯТНОСТЕЙ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
КОМБИНАТОРИКА, ТЕОРИЯ ВЕРОЯТНОСТЕЙ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ.
КОМБИНАТОРИКА, ТЕОРИЯ ВЕРОЯТНОСТИ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ.
Раздел 1. Теоретический материал
1.1 Математика, 5 класс
Комбинаторные задачи.
В повседневной жизни часто приходится создавать различные комбинации, например: денежных купюр различного достоинства, чтобы получить нужную сумму; блюд для обеда; материалов для ремонта и т. п. при этом возникает вопрос: «Сколькими способами можно составить ту или иную комбинацию?». В поисках ответа на него мы решаем особую задачу. В ней заданы элементы комбинирования, а требуется найти количество возможных комбинаций. Такие задачи используют различные способы. Мы ознакомимся с двумя из них.
1.Способ перебора.
Задача 1. Сколькими способами можно составить расписание трех первых уроков в 5 классе из предметов: математика, украинский язык, история?
Решение. Введем обозначения: математика- М, украинский язык- У, история- И.
Если на первый урок поставить математику, тогда на второй- или украинский язык, или историю, а на третий- или историю, или украинский язык соответственно. Получили 2 комбинации: МУИ и МИУ. Рассуждая аналогично, получим еще 4 комбинации: УМИ и УИМ, ИМУ и ИУМ. Итак, расписание можно составить 6 способами.
Чтобы перебрать все комбинации заданных элементов и не потерять какую- либо из них, стоит записывать промежуточные результаты, например в таблице.
Применяя способ перебора, кроме таблицы можно создать дерево возможных вариантов. Это схема, которая помогает выявить все возможные комбинации заданных элементов. Рассмотрим пример.
Задача 2.
Сколькими способами можно разместить на столе в один ряд учебник, тетрадь и дневник?
Решение. Введем обозначения: учебник- У, тетрадь- Т, дневник- Д. Очевидно, что уже образовалась первая комбинация. Запишем ее в один ряд и обведем каждую букву квадратиком. От каждого квадратика проведем по 2 ветки, показывающие, что перебирать осталось из 2 элементов. На концах веток разместим квадратики, в которые впишем обозначения этих элементов. Осталось взять по 1 элементу, поэтому проводим по 1 ветке от каждого квадратика второго уровня и вписываем в них соответствующие элементы. Теперь посчитаем количество квадратиков в низшем, третьем уровне. Их оказывается 6. Итак, учебник, тетрадь и дневник можно разместить 6 способами.
Чтобы выписать эти комбинации, пройдем каждой цепочкой ветвей от самого высокого до самого низкого уровня: УТД, УДТ, ТУД, ТДУ, ДУТ,ДТУ.
В дереве возможных вариантов:
столько уровней, сколько задано элементов для комбинирования;
на каждом уровне проводят столько веток, сколько элементов осталось перебрать.
2. Правило умножения.
Задача 3. В финал соревнований по прыжкам в длину вышли Олег, Игорь, Миша и Дима. Сколькими способами могут распределиться первые 4 места на этих соревнованиях?
Решение. Первое место может завоевать один из четырех мальчиков. Тогда второе место- один из трех оставшихся мальчиков, третье- один из двух оставшихся мальчиков, а четвертое- только один мальчик. Итак, всех возможных вариантов: 4×3×2×1=24.
Правило умножения (для комбинаторных задач).
Чтобы найти количество всех комбинаций из n элементов, нужно умножить все натуральные числа, начиная с числа n и заканчивая числом 1.
Задачи.
1. Выпишите все возможные комбинации цифр 1,2,3,4. Постройте дерево возможных вариантов.
2. На гору ведут три дороги. Петя, Коля и Вася решили подняться на гору разными дорогами. Сколькими способами это можно это сделать?
3. Сколько наборов слов можно составить из слов СОЛНЦЕ, ЗВЕЗДЫ, НЕБО.
4. Сколько трехзначных чисел можно составить из цифр 4, 2, 5 так, чтобы первой стояла цифра 5.
5. Сколько пятизначных чисел можно составить из цифр 1,2,3,4,5?
1.2 Математика, 6 класс.
1.2.1.Случайные события.
Мы часто слышим, а иногда и говорим «это возможно», «это невозможно», «этого никогда не будет», «это обязательно случится», «это маловероятно» и т. д. Наверное, сегодня будет дождь; возможно, завтра я пойду в лес; вероятно, этот мультфильм будет интересным и т. д. Так мы говорим тогда, о наступлении события, которое в одних и тех же условиях может произойти или не произойти. Такое событие называют случайным.
Пример 1. В корзине есть красные и зеленые яблоки. Не заглядывая в корзину, наугад вынимаем одно яблоко. Можно ли заранее сказать, какого цвета будет яблоко?
Конечно, нет. Может произойти одно из двух событий: «взятое яблоко окажется красным», «взятое яблоко окажется зеленым».
Пример 2. В корзине 7 красных и 2 зеленых яблока. Не заглядывая в корзину, наугад берут одно яблоко. Можно ли заранее сказать, какого цвета будет яблоко?
Мы уже знаем, что заранее сказать, какого цвета будет яблоко, невозможно, но, скорее всего, яблоко будет красным, потому что их в корзине больше. Взять красное яблоко из корзины в этом случае более вероятно, чем зеленое.
Пример 3. В корзине есть 3 красных и 3 зеленых яблока. Не заглядывая в корзину, наугад берут из нее яблоко. Какое из событий может произойти: А- «взяли красное яблоко»; В- «взяли желтое яблоко»; С- «взяли зеленое яблоко»; Д- «взяли яблоко»?
Из корзины можно взять только то, что в ней есть, потому вынуть из корзины желтое яблоко невозможно. Потому событие В при данных условиях невозможно.
Так как в корзине есть только яблоки, то любой предмет, вынутый из корзины, является яблоком. Итак, при данных условиях событие Д произойдет обязательно. Говорят, что это событие является достоверным.
События А и С при данных условиях являются случайными, поскольку взятое яблоко может бать как красным, так и зеленым. Так как красных и зеленых яблок в корзине поровну, то эти случайные события являются равновероятными.
Задачи.
1. Определите, какое из событий является невозможным, достоверным, случайным:
а) после зимы наступит осень;
б) в выбранном наугад учебнике будет 288 страниц;
в) 20 июля в Одессе выпадет снег;
г) 1 января в Украине начнется новый год;
д) у одного из пассажиров автобуса, в котором я еду, сегодня день рождения;
е) завтра будет хорошая погода.
2. Определите, какое из событий является невозможным, достоверным, случайным:
а) я выиграю в лотерею, так как приобрел 3 билета;
б) завтра я встречу живого динозавра;
в) подброшу монету, и выпадет «орел»;
г) по дороге в школу я встречу знакомого, которого не видел 2 года;
д) следующим днем после уторника будет середа;
е) следующим днем после среды будет вторник.
3. Сравните возможность наступления случайных событий, использовав для этого выражения «более вероятно», «менее вероятно», «равновероятно»:
а) вы проснулись утром:
А: сегодня рабочий день; В: сегодня выходной день;
б) вы подбросили игральный кубик:
А: выпадет число, кратное 3; В: выпадет число, кратное 2.
4. сравните возможность наступления случайных событий, использовав для этого выражения «более вероятно», «менее вероятно», «равновероятно»:
а) вы включили телевизор:
А: транслируют футбольный матч; В: демонстрируют фільм;
б) вы летом проснулись и раздвинули шторы:
А: за окном летняя ночь; В: за окном летний дождь;
в) вы подбросили монету:
А: выпадет «орел»; В: выпадет «решка».
5. Есть 10 карточек, пронумерованных числами от 1 до 10. Максим наугад берет одну из этих карточек. Какое событие является более вероятным:
а) «Максим выбрал карточку с числом больше 5» или «Максим выбрал карточку с числом меньше 5»;
б) «Максим выбрал карточку с числом, кратным 3» или «Максим выбрал карточку с числом, кратным 4»;
в) «Максим выбрал карточку с числом, которое делится на 4», или «Максим выбрал карточку с числом, которое делится на 5»?
1.2.2 Вероятность случайного события.
Случайные события могут быть более вероятными, менее вероятными, равновероятными, то есть случайное событие можно охарактеризовать понятием вероятность. Понять это помогут следующие примеры.
Пример 1. На столе лежит 8 внешне одинаковых тетрадей, из них одна в клетку, а остальные- в линейку. Ученик хочет взять тетрадь в клетку. Имеется 8 равновероятных случаев взять тетрадь, и только одном из них она будет в клетку. Поэтому считают, что вероятность того, что взятая наугад тетрадь будет тетрадью в клетку, равна 1/8. Отношение 1/8 является вероятностью события: взятая тетрадь будет тетрадью в клетку.
Пример 2. В лотерею разыгрывается 1000 билетов, из них 10- выигрышные. Какова вероятность того, что купленный билет будет выигрышным?
Имеем 1000 равновероятных случаев купить билет лотереи, и только в 10 случаях он будет выигрышным. Отношение 10/1000=1/100 является вероятностью события: билет будет выигрышным.
Задачи.
В магазине 1000 батареек, из них 4 бракованных. Какова вероятность того, что купленная батарейка будет: а) бракованной; б) не бракованной?
Выпустили 100000 лотерейных билетов, из них 2500- выигрышные. Какова вероятность того, что купленный билет будет: а) выигрышным: б) невыигрышным.
В коробке 20 белых и 5 желтых шаров. Какова вероятность того, что наугад вынутый шар окажется белым, желтым?
В вазе 8 шоколадных конфет и 12 карамелек. Не заглядывая в вазу Надя наугад взяла одну конфету. Какова вероятность того, что Надя взяла: а) шоколадную конфету; б) карамельку?
Из натуральных чисел от 1 до 24 Олег наугад называет одно число. Какова вероятность того, что число будет делителем числа 24?
1.3 Математика, 9 класс.
1.3.1 Частота и вероятность случайного события.
Нам нередко приходится проводить наблюдения, опыты, участвовать в экспериментах или испытаниях. Часто подобные исследования заканчиваются некоторым результатом, который заранее предсказать нельзя.
Рассмотрим несколько характерных примеров.
Если открыть книгу наугад, то невозможно знать заранее, какой номер страницы вы увидите.
Нельзя до начала футбольного матча определить, с каким счетом закончится игра.
Вы не можете быть уверенным в том, что, когда нажмете на кнопку выключателя, загорится настольная лампа.
Нет гарантии, что из куриного яйца, помещенного в инкубатор, вылупится цыпленок.
Как правило, наблюдения или эксперимент определяются каким-то комплексом условий. Например, футбольный матч должен проходить по правилам; куриные яйца должны находиться в инкубаторе не менее 21 дня при определенной методике изменения температуры и влажности воздуха.
Результат наблюдения, опыта, эксперимента будем называть событием.
Случайным событием называют такой результат наблюдения или эксперимента, который при соблюдении данного комплекса условий может произойти, а может и не произойти.
Например, при подбрасывании однородной монеты случайным событием является выпадение цифры. Обнаружение письма при проверке почтового ящика также является случайным событием.
Представим, что выпущен 1 000 000 лотерейных билетов и разыгрывается один автомобиль. Можно ли, приобретя один лотерейный билет, выиграть этот приз? Конечно, можно, хотя это событие маловероятно. А если будут разыгрываться 10 автомобилей? Ясно, что вероятность выигрыша увеличится. Если же представить, что разыгрываются 999 999 автомобилей, то вероятность выигрыша станет намного большей.
Следовательно, вероятности случайных событий можно сравнивать. Однако для этого следует договориться, каким образом количественно оценивать возможность появления того или иного события.
Основанием для такой количественной оценки могут быть результаты многочисленных наблюдений или экспериментов. Так, люди давно заметили, что многие события происходят с той или иной, на удивление постоянной, частотой.
Демографам хорошо известно число 0,514. Статистические данные, полученные в разные времена и в разных странах, свидетельствуют о том, что на 1000 новорожденных приходится в среднем 514 мальчиков. Число 0,514 называют частотой случайного события «рождение мальчика». Оно определяется формулой
Частота = (количество новорожденных мальчиков)/(количество всех новорожденных).
Подчеркнем, что это число получено в результате анализа многих наблюдений. В таких случаях говорят, что вероятность события «рождение мальчика» приблизительно равна 0,514.
Вы знаете, что курение вредно для здоровья. По данным Всемирной организации здравоохранения (ВОЗ) курильщики составляют приблизительно 97 % от всех больных раком легких. Число 0,97 — это частота случайного события «тот, кто заболел раком легких,— курил», которая определяется таким соотношением:
Частота = (количество курильщиков среди заболевших раком легких)/(количество всех людей, заболевших раком легких).
Это впечатляющее число 97 % может у кого-то вызвать сомнения. Однако мы хотим подчеркнуть, что частота случайного события тем лучше характеризует явление, чем больше наблюдений проведено. Вывод ВОЗ основывается на анализе многих наблюдений, проведенных в разных странах, следовательно, касается всех людей.
В таких случаях говорят, что вероятность попасть на курильщика среди тех, кто заболел раком легких, приблизительно равна 0,97 (или 97 %).
Чтобы детальнее ознакомиться с понятием вероятности случайного события, обратимся к классическому примеру с подбрасыванием монеты.
Предположим, что в результате двух подбрасываний монеты дважды выпал герб. Тогда в данной серии, состоящей из двух испытаний, частота выпадения герба равна:
Частота = (количество выпадений герба)/( количество бросков )=2/2
Означает ли это, что вероятность выпадения герба равна 1? Конечно, нет.
Для того чтобы по частоте случайного события можно было оценивать его вероятность, количество испытаний должно быть достаточно большим.
Начиная с XVIII в. многие исследователи проводили серии испытаний с подбрасыванием монеты.
По этим данным прослеживается четкая закономерность: при многократном подбрасывании монеты частота появления герба незначительно отклоняется от числа 0,5.
Следовательно, можно считать, что вероятность события «выпадение герба» приблизительно равна 0,5.
В каждом из рассмотренных примеров использовалось понятие частота случайного события. Эту величину мы вычисляли по формуле:
Частота =( количество появлений интересующего события)/(количество испытаний (наблюдений))
Далее по частоте мы оценивали вероятность события, а именно:
вероятность случайного события приближенно равна частоте этого события, найденной при проведении большого количества испытаний (наблюдений ).
Такую оценку вероятности случайного события называют статистической. Ее используют в разных областях деятельности человека: физике, химии, биологии, страховом бизнесе, социологии, экономике, здравоохранении, спорте и т. д.
Вероятность события обозначают буквой Р (первой буквой французского слова probabilite — вероятность).
Если в первом примере событие «рождение мальчика» обозначить буквой А, то полученный результат записывают так:
Р (А) = 0,514.
Если событие «выпадение герба» обозначить буквой В, то
Р (В) = 0,5.
Задачи.
1. Оператор справочной службы в течение рабочего дня (9:00-17:00) разговаривает в среднем по телефону 6 ч. Оцените вероятность того, что, если позвонить в справочную в это время, телефон окажется свободным.
2. По статистике, в городе Одесса в течение лета количество солнечных дней в среднем равно 70. Оцените вероятность того, что, приехав летом в Одессу на один день, гость застанет пасмурную погоду.
3. Во время эпидемии гриппа среди обследованных 40 ООО жителей выявили 7900 больных. Оцените вероятность события «наугад выбранный житель болен гриппом».
4. Вероятность купить бракованную батарейку равна 0,02. Верно ли, что в любой партии из 100 батареек есть две бракованные?
5. Выберите наугад одну страницу из повести Марко Во- вчок «Институтка». Подсчитайте, сколько на этой странице окажется букв «н», «о», «я», «ю», а также сколько всего на ней букв. Оцените вероятность появления этих букв в выбранном тексте. Эта оценка позволит понять, почему на клавиатурах пишущей машинки и компьютера (рис. 85) буквы «н» и «о» расположены ближе к центру, а буквы «я» и «ю» — ближе к краю.

1.3.2| Классическое определение вероятности
Для нахождения вероятности некоторых событий не обязательно проводить испытания или наблюдения. Достаточно руководствоваться жизненным опытом и здравым смыслом.
ПРИМЕР 1
Пусть в коробке лежат 10 красных шариков. Какова вероятность того, что взятый наугад шарик будет красного цвета? желтого цвета?
Очевидно, что при испытании в данных условиях любой взятый наугад шарик будет красного цвета.
Событие, которое при данном комплексе условий обязательно состоится при любом испытании, называют достоверным. Вероятность такого события считают равной 1, то есть :если А — достоверное событие, то Р(А) = 1.
Также очевидно, что при любом испытании шарик не может быть желтого цвета, ведь в коробке их нет.
Событие, которое при данном комплексе условий не может состояться ни при каком испытании, называют невозможным. Вероятность такого события считают равной 0, то есть: если А — невозможное событие, то Р (А) = 0.
Заметим, что для любого события А выполняется неравенство 0
ПРИМЕР 2
Рассмотрим эксперимент, состоящий в том, что однородную монету подбрасывают один раз.
Понятно, что можно получить только один из двух результатов (исходов): выпадение цифры или выпадение герба. Причем ни один из них не имеет преимуществ. Такие результаты называют равновозможными, а соответствующие случайные события равновероятными. Тогда естественно считать, что вероятность каждого из событий «выпадение герба» и «выпадение цифры» равна ½.
Подчеркнем: это совсем не означает, что в любой серии экспериментов с подбрасыванием монеты половиной результатов будет выпадение герба. Мы можем лишь прогнозировать, что при большом количестве испытаний частота выпадения герба приблизительно будет равной ~.
Рассмотрим еще несколько примеров, в которых ключевую роль будут играть равновозможные результаты.
ПРИМЕР 3
Пусть выпущен 1 000 000 лотерейных билетов, 10 из которых являются выигрышными. Испытание состоит в том, что покупают один билет. Этот эксперимент приводит к 1 000 000 равновозможных результатов: купили первый билет, купили второй билет и т. д. Тогда вероятность выигрыша при покупке одного билета равна 10/1000000=1/100000.
ПРИМЕР 4
Пусть в коробке лежат 15 бильярдных шаров, пронумерованных числами от 1 до 15. Какова вероятность того, что вынутый наугад шар будет иметь номер, кратный 3?
Понятно, что в этом испытании есть 15 равновозможных
результатов. Из них существует 5, которые нас устраивают:
когда вынимают шары с номерами 3, б, 9, 12, 15. Поэтому
естественно считать, что вероятность события «вынули шар
с номером, кратным 3» равна 5/15=1/3.
Несмотря на то, что в примерах 1-4 рассматривались разные ситуации, их описывает одна математическая модель. Поясним это.
В каждом примере при испытании можно получить один из п равновозможных результатов.
Пример 1: n = 10.
Пример 2: n = 2.
Пример 3: n = 10000000.
Пример 4: n = 15.
В каждом примере рассматривается некоторое событие А, к которому приводят т результатов. Будем называть их благоприятными.
Пример 1: А — вынули красный шарик, т = 10, или А — вынули желтый шарик, т = 0.
Пример 2: А — выпал герб, т = 1.
Пример 3: А — выигрыш приза, т = 10.
Пример 4: А — вынули шар, номер которого кратен 3, т = 5.
В каждом примере вероятность события А можно вычислить по формуле:
Р (А) = m/n.
Определение Если испытание заканчивается одним из п равновозможных результатов, из которых т приводят к наступлению события А, то вероятностью события А называют отношение m/n.
Такое определение вероятности называют классическим.
В завершение этого пункта отметим следующее.
На первый взгляд кажется, что многими явлениями, происходящими вокруг нас, управляет «его величество случай». Однако при более основательном анализе выясняется, что через хаос случайностей прокладывает себе дорогу закономерность, которую можно количественно оценить. Науку, которая занимается такими оценками, называют теорией вероятностей.
Задачи.
1. Какова вероятность того, что, переставив буквы в слове «алгебра», мы получим слово «геометрия»?
2. Представь себе, что в классе, в котором ты учишься, разыгрывается одна бесплатная туристическая поездка в Лондон. Какова вероятность того, что в Лондон поедешь ты?
3.Чтобы сдать экзамен по математике, надо выучить 35 билетов. Ученик выучил безупречно 30 билетов. Какова вероятность того, что, отвечая на один
наугад вытянутый билет, он получит оценку 12 баллов?
4. Какова вероятность того, что при одном бросании игрального кубика выпадет количество очков, равное: одному; трем; четному числу; числу, кратному 5; числу, которое не делится нацело на 3; числу, кратному 7?
1.4 Математика, 11 класс.
1.4.1 Комбинаторика. Правила суммы и произведения.
Вспомните, что в математике любые совокупности называют множествами. Объекты, входящие в множества, называют его элементами. Множества обозначают большими латинскими буквами, а их элементы записывают в фигурных скобках. Считают, что все элементы множества различны.
Например, А = {а, b, с}, М = {1, 5, 7, 9}.
Множества бывают конечными и бесконечными. Если множество не содержит ни одного элемента, его называют пустым и обозначают символом 0.
Два множества называют равными, если они состоят из одних и тех же элементов.
Если А — часть множества В, то его называют подмножеством множества В и записывают A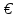 B. Наглядно это изображают с помощью диаграммы Эйлера (рис. 135, а). В частности, для числовых множеств правильные такие соотношения: N € Z,N€Q.
B. Наглядно это изображают с помощью диаграммы Эйлера (рис. 135, а). В частности, для числовых множеств правильные такие соотношения: N € Z,N€Q.
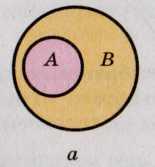
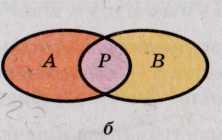
Случается, что множества А и В имеют общие элементы. Если множество Р содержит все общие элементы множеств А и Б и только их, то множество Р называют пересечением множеств А и Б. Записывают это так: А ∩ В = Р. Диаграммой Эйлера пересечение изображают, как показано на рисунке 135, б. Множество, содержащее каждый элемент каждого из множеств А и В и только эти элементы, называется объединением множеств А и В. Если К — объединение множеств А и В, то пишут A U В = К (рис. 135, в).
Рис. 135
Разницей множеств А и В называют множество, состоящее из всех элементов множества А, не принадлежащих множеству В. Его обозначают А \ В. Например, если А = {1, 2, 3, 4}, В = {1, 4, 5, 7, 8}, то А ∩ В = {1, 4}, A U В = {1, 2, 3, 4, 5, 7, 8 },А\В = {2, 3}.
Говоря «множество», «подмножество», порядок их элементов не учитывают. Говорят, что они не упорядочены. Рассматривают и упорядоченные множества. Так называют множества с фиксированным порядком элементов. Их обозначают не фигурными, а круглыми скобками. Например, из элементов множества {а, b, с} можно образовать 6 трёхэлементных упорядоченных множеств: (а, b, с), (а, с, b), (b, а, с), (b, с, а), (с, а, b), (с, b, а).
Как множества, все они равны, как упорядоченные множества — разные.
Существуют задачи, в которых надо определить, сколько различных подмножеств или упорядоченных подмножеств можно образовать из элементов данного множества. Их называют комбинаторными задачами, а раздел математики, в котором рассматривается решение комбинаторных задач, называют комбинаторикой.
Комбинаторика — раздел математики, посвящённый решению задач выбора и расположения элементов некоторого конечного множества в соответствии с заданными правилами.
Рассмотрим два основных правила, с помощью которых решается много комбинаторных задач.
Задача 1.В городе N есть два университета — политехнический и экономический. Абитуриенту нравятся три факультета в политехническом университете и два — в экономическом. Сколько возможностей имеет студент для поступления в университет?
Решение. Обозначим буквой А множество факультетов, которые выбрал абитуриент в политехническом университете, а буквой В — в экономическом: А = {m,.n, к), В = {р, s}. Поскольку эти множества не имеют общих элементов, то в целом абитуриент имеет 3 + 2 = 5 возможностей для поступления в университет.
Описанную ситуацию можно обобщить в виде утверждения, которое называется правилом суммы.
| Если элемент некоторого множества A можно выбрать m способами, а элемент множества В — n способами, то элемент из множества А или из множества В можно выбрать m+ n способами.
Правило суммы распространяется и на большее количество множеств.
Задача 2. Планируя летний отдых, семья определилась с местами его проведения: в Одессе — 1, в Евпатории — 3, в Ялте — 2, в Феодосии — 2. Сколько возможностей выбора летнего отдыха имеет семья?
Решение. Поскольку все базы отдыха разные, то для решения задачи достаточно найти сумму элементов всех множеств, о которых говорится: 1 + 3 + 2 + 2 = 8. Следовательно, семья может выбирать отдых из 8 возможных.
Задача З.От пункта А до пункта В ведут три тропинки, а от Б до С — две. Сколько маршрутов можно проложить от пункта А до пункта С?
Решение. Чтобы пройти от пункта А до пункта В, надо выбрать одну из трёх тропинок: 1, 2 или 3 (рис. 136). После этого следует выбрать одну из двух других троп: 4 или 5. Всего от пункта А до пункта С ведут 6 маршрутов, потому что 3-2 = 6. Все эти маршруты можно обозначить с помощью пар:
(1; 4), (1; 5), (2; 4), (2; 5), (3; 4), (3; 5).
Обобщим описанную ситуацию.
! Если первый компонент пары можно выбрать m способами, а второй — n способами, то такую пару можно выбрать mn способами.
Это — правило произведения, его часто называют основным правилом комбинаторики. Обратите внимание: речь идёт об упорядоченных парах, составленных из различных компонентов.
Правило произведения распространяется и на упорядоченные тройки, четвёрки и любые другие упорядоченные конечные множества. В частности, если первый компонент упорядоченной тройки можно выбрать т способами, второй — п способами, третий — k способами, то такую упорядоченную тройку можно выбрать mnk способами. Например, если столовая на обед приготовила 2 первых блюда — борщ (б) и суп (с ), 3 вторых — котлеты (к), вареники (в), голубцы (г) и 2 десертных — пирожные (п) и мороженое (м), то всего из трёх блюд столовая может предложить 12 различных наборов, поскольку 2 • 3 • 2 = 12.

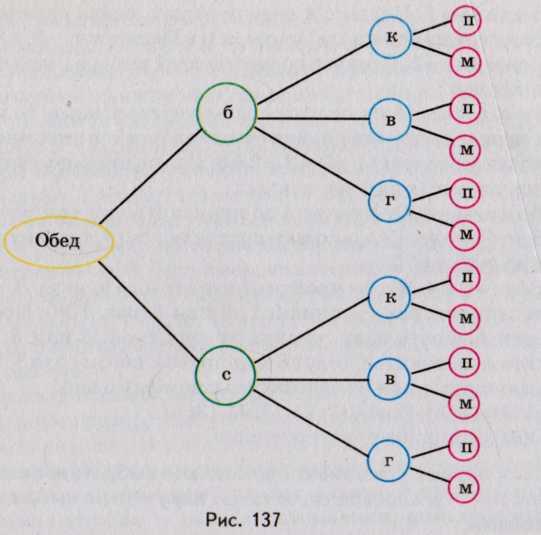
Описанной ситуации соответствует диаграмма, изображённая на рисунке 137. Такие диаграммы называют деревьями.
Задача 4. Сколько разных поездов можно составить из 6 вагонов, если каждый из вагонов можно поставить на любом месте?
Решение. Первым можно поставить любой из 6 вагонов. Имеем 6 выборов. Второй вагон можно выбрать из оставшихся 5 вагонов. Поэтому, согласно правилу умножения, два первых вагона можно выбрать 6 ×5 способами. Третий вагон можно выбрать из 4 вагонов, которые остались. Поэтому три первых вагона можно выбрать 6×5×4 способами. Продолжая подобные рассуждения, приходим к ответу: всего можно составить 6×5×4×3×2×1 = 720 различных поездов.
Обратите внимание на решение последней задачи. Оно свелось к вычислению произведения всех натуральных чисел от 1 до 6. В комбинаторике подобные произведения вычисляют часто.
Произведение всех натуральных чисел от 1 до n называют га факториалом и обозначают n!
Например:
5! = 1×2×3×4×5 = 120, 7! = 1×2×3×4×5× 6×7 = 5040.
Условились считать, что 1! = 1 и 0! = 1.
Языком теории множеств правила суммы и произведения можно сформулировать следующим образом.
Если пересечение множеств А и В пустое, то количество элементов в их объединении n (A U В) равно сумме количества элементов множеств А и В: n(AUB) = n(А) + n(В).
Если множества А иВ имеют общие элементы, то
n(А U В) = n(А) + n(В) - n(А ∩ В).
Если множества А и В конечны, то количество возможных пар (а, b), где а € А,b€ В, равно произведению количества элементов множеств А и В:
n(А∩В) = n(А)+ n(В).
Задачи.
1. Задайте перечнем элементов множество одноцифровых чисел, которые делятся: а) на 2; б) на 3; в) на 5; г) на 11.
2. Вычислите:
а) 0!; 6)1!; в) 6!; г) 8!; д) 10!.
3. В магазине есть три вида печенья и десять видов конфет. Сергей хочет купить сестре печенье или конфеты. Сколькими способами он может это сделать?
4.Для завершения формирования экспедиции в Антарктиду дополнительно рассматривались заявления 10 претендентов на должность врача, 5 претендентов на пост повара и 3 претендентов на должность техника. Ни один кандидат не претендовал одновременно на две или более должностей. Сколькими способами можно заполнить одно свободное место в экспедиции. 5.Сколькими способами 5 человек могут образовать очередь в кассу?
6.Сколько различных предложений можно написать словами «мы», «любим», «играть»? А словами «мы», «очень», «любим», «играть»?
1.4.2 . РАЗМЕЩЕНИЯ И ПЕРЕСТАНОВКИ
Задача 1. Сколькими способами собрание из 20 человек может избрать председателя и секретаря?
Решение. Председателя можно выбрать 20-ю способами, секретаря — из остальных 19 человек — 19-ю способами. По правилу произведения председателя и секретаря собрания могут выбрать 20×19 = 380 способами.
Обобщим задачу. Сколько упорядоченных k-элементных подмножеств можно составить из п различных элементов? На первое место можно поставить любой из данных п элементов. На второе место — любой из остальных n - 1 элементов и т. д. На последнее k-e место можно поставить любой из остальных n — k + 1 элементов. Из правила произведения следует, что из данных n элементов можно получить n(n - 1)(n - 2) ... (n - k + 1) k-элементных упорядоченных подмножеств.
Например, из 4 элементов а, b, с, d упорядоченных двухэлементных подмножеств можно образовать всего 4×3 = 12: (а; b), (а; с), (а; d), (b; а), (b; с), (b; d), (с; а), (с; b), (с; d), (d; a), (d; b), (d; с).
Упорядоченое k-элементное подмножество n-элементного множестваназывают размещением из n элементов по k. Их число обозначают 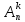 .
. 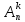 =n • (n — 1) •... • (n - k + 1).
=n • (n — 1) •... • (n - k + 1).
В правой части этого равенства k множителей. Поэтому результат можно сформулировать в виде такого утверждения.
Число размещений из n элементов по к равно произведению k последовательных натуральных чисел, наибольшее из которых n.
Число размещений из п элементов по k можно вычислять и по другой формуле: 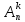 =
=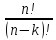 .
.
Размещение n элементов по n называют перестановками из n элементов. Их число обозначают 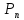 .
.
Например, из трёх элементов а, b, с можно образовать 6 различных перестановок: abc, acb, bac, bca, cab, cba.
Следовательно, 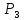 =6.
=6.
Подставив в формулу числа размещений k=n. получим. что 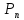 =n!.
=n!.
Число перестановок из n элементов равно n!
Примеры. 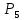 = 1×2×3×4×5 = 120;
= 1×2×3×4×5 = 120;
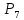 = 1×2×3×4×5×6×7 = 5040.
= 1×2×3×4×5×6×7 = 5040.
Некоторые комбинаторные задачи сводятся к решению уравнений, в которых переменная указывает на количество элементов в некотором множестве или подмножестве.
Задачи.
Сколькими способами 4 ученика могут сесть за двумя двухместными партами?
Сколькими способами можно поздравить маму и бабушку с праздником, если вы имеете 3 разные открытки?
3. Сколькими способами 6 учеников могут сесть за тремя двухместными партами?
4. На тарелке есть 7 груш. Пятеро детей берут из неё по одной груше. Сколькими способами это можно сделать?
5. Сколько разных трехзначных чисел можно написать цифрами 6, 7 и 8 так, чтобы все цифры каждого числа были разные?
6. В начальной школе 11 классов и 11 учителей классоводов. Сколькими способами можно распределить классы между учителями?
7. В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
1.4.3 КОМБИНАЦИИ И БИНОМ НЬЮТОНА
Пусть дано множество из трёх элементов: {а, b, с}. Его двухэлементных подмножеств (не упорядоченных) существует всего три: {а, b}, {а, с}, {b, с}. Говорят, что существует 3 комбинации из трёх элементов по два. Пишут: 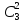 =3.
=3.
Комбинацией из n элементов по k называют любое k-элементное подмножество n-элементного множества.
Число комбинаций из n элементов по k обозначают 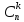 . В отличие от размещений, комбинации — подмножества неупорядоченные.
. В отличие от размещений, комбинации — подмножества неупорядоченные.
Число k-элементных комбинаций в 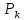 раз меньше числа размещений из тех же k элементов.
раз меньше числа размещений из тех же k элементов.
То есть 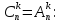
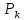 , отсюда
, отсюда
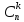 =
=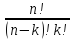 или
или 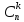 =
=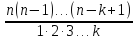 .
.
Обратите внимание! 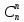 =1,
=1, 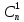 = n. Полагают также, что
= n. Полагают также, что 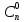 = 1 для любого n
= 1 для любого n N.
N.
Можно доказать, что для натуральных значений n и k (n k) правильно тождество
k) правильно тождество 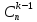 +
+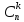 =
=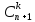 .
.
С комбинациями тесно связана формула бинома Ньютона. Вспомните формулу квадрата двучлена: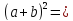
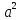 +2ab+
+2ab+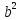 . Умножив
. Умножив 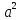 +2ab+
+2ab+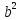 на а + b и на
на а + b и на 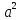 +2ab+
+2ab+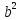 , получим форм2улы:
, получим форм2улы: 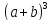 =
=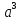 +3
+3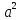 b+3a
b+3a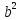 +
+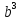 ,
,
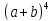 =
=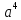 +4
+4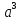 b+6
b+6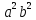 +4a
+4a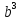 +
+.
Эти три формулы можно записать и так:
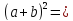
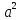 +
+ab+
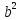 ,
,
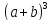 =
=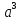 +
+b+
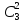 a
a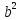 +
+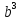 ,
,
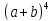 =
=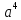 +
+b+
+
a
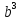 +
+.
Оказывается, для каждого натурального значения n правильна и общая формула: =
+
b+
+…+
+
(*)
Это тождество называют формулой бинома Ньютона, а её правую часть разложением бинома Ньютона. Бином — латинское название двучлена. Пользуясь этой формулой, возведём, например, двучлен а + b в пятую степень. Поскольку =5,
=10,
=10,
=5, то
=
+5
+10
+10
+5a
+
.
Доказать формулу бинома Ньютона можно методом математической индукции.
Доказательство. Предположим, что формула (*) верна для некоторого натурального показателя степени n. Покажем, что тогда она верна и для следующего за ним значения n + 1.
=
(a+b)= = =(
+
+
…+
a
+
)(a+b)=
+
b+
+…+
+a
+
b+
+…+
a
+
=
+(
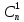 +1)
+1)b+(
+
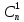 )
)+…+(
+1)a
+
=
+
+
Выражения в скобках преобразованы согласно формулы
Следовательно, если формула бинома Ньютона верна для n, то она правильна и для n + 1. Для n = 1 она правильна, так как Поэтому на основе аксиомы математической индукции можно утверждать, что формула верна для любого натурального показателя n.
Вычислять коэффициенты разложения бинома Ньютона можно не по формуле числа комбинаций, а пользуясь числовым треугольником Паскаля — своеобразным способом вычисления коэффициентов разложения бинома Ньютона
Треугольник Паскаля можно продолжать как угодно далеко.
Это следует из тождества . Его крайние числа —
единицы, а каждое другое равно сумме двух ближайших к нему чисел сверху.
Например, прибавляя числа шестой строки (для п = 5), получим числа следующей строки (для n = 6): 1,6,15, 20,15, 6,1. Следовательно, . Общий член разложения бинома можно определить по формуле
где k=0,1,2,3,… .
Например: первый член - ;
второй член - ;
третий член - .
Задачи.
В классе 32 ученика. Сколькими способами можно выбрать из них двух дежурных?
В соревнованиях участвует 12 человек. Сколько существует способов занять призовое место (1-е, 2-е или 3-е)?
Сколькими способами можно распределить 6 одинаковых шоколадок между тремя детьми, чтобы каждый ребёнок получил 2 шоколадки? А если все шоколадки разные?
Для опыта взяли 3 белых, 5 красных и 7 розовых цветков гороха из имеющихся 10-ти белых, 10-ти красных и 10-ти розовых цветков. Сколькими способами это можно сделать?
В баскетбольной команде, состоящей из 15 человек, нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Сколькими способами можно раздать 28 пластинок домино четырём игрокам, чтобы каждому досталось 7 пластинок?
1.4.4 СВЕДЕНИЯ О СТАТИСТИКЕ
Статистика — это наука, которая занимается сбором, обработкой и изучением различных данных, связанных с массовыми явлениями, процессами и событиями. Статистические сведения о какой-то большой совокупности объектов (генеральной совокупности) получают в основном в результате анализа только незначительной её части — выборки. Чтобы узнать, например, о наиболее распространённом размере мужской обуви, достаточно опросить несколько десятков мужчин. Предположим, что, опросив 60 мужчин, получили результаты, приведённые в таблице:
Размер обуви 25 25,5 26 26,5 27 27,5 28 28,5 29 29,5 30 30,5
Количество мужчин 1 2 3 7 10 9 8 8 6 4 1 1
Это — частотная таблица, в ней числа второй строки — частоты. Например, частота обуви размера 29 равна 6. Относительная частота этого размера 6:60 = 0,1 = 10%.
Проанализировав такую выборку, делают общий вывод: примерно 10 % мужской обуви надо делать 29 размера, а размера 26 — вдвое меньше. Это — приближённые отношения, но для практики таких приближений бывает достаточно.
Математическим анализом различных выборок занимается математическая статистика. Её основная задача — разрабатывать эффективные методы изучения больших совокупностей объектов на основе сравнительно небольших выборок.
Каждый элемент выборки называют её вариантой. Выборка, полученная в результате наблюдений, бывает неупорядоченной. Упорядочив её, получают вариационный ряд. Разность между крайними членами вариационного ряда —размах выборки. Пусть дано выборку
4, 3, 7, 9, 6, 8, 2, 6, 1, 7, 7, 3, 2, 5.
Упорядочив её по возрастанию вариант, получим вариационный ряд:
2, 2, 3, 3, 4, 5, 6, 6, 7, 7, 7, 8, 9.
Размах данной выборки r = 9 - 1 = 8.
Мода выборки — её варианта с наибольшей частотой (обозначается Мо). Медиана выборки — число, которое «разделяет» соответствующий вариационный ряд пополам (обозначается Me).
Следовательно, для данной выборки Мо = 7; Me = (5 + 6) = 5,5.
Средним значением выборки называют среднее арифметическое всех её вариант.
Например, если дано выборку 1, 2, 3, 3, 5, 6, 8, то её среднее значение
х = (1+2 + 3 + 3 + 5 + 6 + 8) = 4.
Если варианты выборки повторяются, то суммы равных слагаемых можно заменить произведениями.
Задача. 7 рабочих бригады ежемесячно получают по 3000 грн, 8 — по 4500 грн, а 5 — по 5000 грн. Определите среднюю месячную зарплату рабочего этой бригады.
Решение. Всего рабочих в бригаде 7 + 8 + 5 = 20. Поэтому искомая средняя зарплата
х = (3000×7 + 4500×8 + 5000×5) = 4100.
Ответ. 4100 грн.
Моду, медиану и среднее значение выборки называют центральными тенденциями выборки.
В статистике часто используют и среднее квадратичное. Если дано n чисел , то их среднее квадратичное
определяется по формуле:
.
С помощью среднего квадратичного чаще оценивают совокупности погрешностей или отклонений от нормы. Рассмотрим пример. Желая выточить деталь радиуса R, токарь практически вытачивает деталь радиуса R + а, где а — некоторое отклонение (положительное или отрицательное). Пусть два токаря, выточив по 6 таких деталей, допустили такие ошибки (в десятых долях миллиметра):
первый: 2, -5, 4, -3, -3, 5;
второй: 3, -1, 4, 1, 1, 2.
Кто из них выполнил задание качественнее?
Чтобы ответить на вопрос, вычисляют средние квадратичные допущенных отклонений:
==
≈3,8 ;
==
≈2,3 .
Качественнее работу выполнил второй токарь.
Если разности между вариантами выборки и её средним значением равны то среднее арифметическое их квадратов называется дисперсией выборки (лат. Dispersio-
рассеяние). Дисперсия равна квадрату среднего квадратичного всех отклонений и вычисляется по формуле: D=
В математике, в частности в математической статистике, нередко используют также среднее геометрическое () и среднее гармоническое (S гарм), вычисляемые по формулам:
; .
Для любого количества положительных чисел
всегда справедливы неравенства .
Задачи.
Дано выборку 3, 1, 4, 1, 2, 3, 4, 3, 1, 2, 1. Постройте соответствующий ей вариационный ряд; найдите размах, моду и медиану выборки.
Выборка включает все натуральные числа меньше 10, а кроме того, числа 6, 8, 8 и 13. Постройте её вариационный ряд. Найдите размах выборки, её моду и медиану.
Варианты 1, 2, 3,4, 5 выборки имеют частоты 3, 4, 6, 2 и 3 соответственно, а всего выборка имеет 18 вариант. Найдите её размах, моду и медиану.
За экзаменационную работу по математике получили 4,5, 6, 7, 8, 9, 10, 11 и 12 баллов соответственно 2, 9, 8, 10, 20, 17, 4, 6 и 4 абитуриента. Составьте частотную таблицу и вычислите относительные частоты баллов, которые встречались наиболее редко и наиболее часто.
Выберите по отрывку (1 страница) художественного произведения двух разных авторов, прочитайте их. Для букв «а», «б», «н», «о», «ч», «я» составьте частотные таблицы их наличия в избранных отрывках. Проанализируйте их.
4.5 ГРАФИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ О ВЫБОРКЕ
Статистические данные сводят в таблицы. Статистическая таблица — это особая форма рационального и систематизированного изложения обобщающих характеристик статистической совокупности. Как и грамматическое предложение, статистическая таблица имеет подлежащее и сказуемое. В подлежащем приводится перечень элементов, явлений, признаков, указанных в таблице. В сказуемом таблицы подаются количественные характеристики. Например, в приведённой ниже таблице сбора зерна в некоторых странах в 1995 г. подлежащим является левая колонка. Числовые данные в других — сказуемое таблицы.
Страна Пшеница Рожь Ячмень Всего
Китай 101 0.6 _ 400
США 67 6,3 9,9 353
Россия 46 13,9 25,5 103
Франция 33 _ 10,5 60
Германия 16 2,4 12,2 35
Украина 19 1,2 10.1 34
Информацию о той или иной выборке часто подают графически, чаще всего в форме диаграмм. Слово диаграмма в переводе с греческого означает рисунок, чертёж. Правда, теперь этим словом называют не любой рисунок, а схематическое изображение отношений между множествами, различные структуры, алгоритмы действий и т. д. Отношения (соотношения) между множествами и объёмами понятий зачастую изображают в виде диаграмм-деревьев или диаграмм Эйлера (рис. 137,135).
Структуры моделей, различные диаграммы классов, состояний удобно подавать в виде круговых (секторных) диаграмм.
На рисунках 144 и 145 на секторной и столбчатой диаграммах изображены соотношения между численностью граждан Украины разных национальностей (согласно переписи 2001 г.).
Столбчатую диаграмму из соединённых прямоугольников называют гистограммой. На рисунке 146 изображена гистограмма, которая соответствует приведённой ниже таблице распределения рабочих цеха по тарифным разрядам.
Тарифный разряд 1 2 3 4 5 6 Всего
Число рабочих 2 2 5 15 20 6 50
Иногда вместо гистограммы строят полигон распределения, соединяя отрезками середины верхних оснований последовательных прямоугольников гистограммы (рис. 147). Бывают и другие диаграммы.
Информацию о динамике того или иного явления графически удобно изображать с помощью столбчатых диаграмм или графиков. Например, на рисунке 148 приведена диаграмма динамики рождаемости в Украине от 1960 до 2002 года; на рисунке 149 —
графики, отражающие динамику количества учеников, классов и школ в сёлах Украины.
В социологии диаграммы часто строят на основе полярной системы координат. На двух следующих диаграммах (рис. 150, 151) большим расстояниям от полюса 0 соответствуют большие значения величин. Проанализируйте эти диаграммы.
Задачи.
Постройте таблицу по данным рисунка 154. Укажите её подлежащее и сказуемое.
Составьте таблицу, которая отражает вашу успеваемость за первое полугодие: а) 10 класса; б) 11 класса. Постройте соответствующую диаграмму.
В Украине придерживаются примерно такой структуры посевных площадей: озимая пшеница — 23 %, другие зерновые культуры — 22 %, кормовые культуры — 37 %,
технические культуры — 12 %, картофель и овощи — 6 %. Постройте соответствующую секторную диаграмму.
Прочитайте диаграмму производства электроэнергии на человека (кВт • ч) в некоторых странах в 1992 г. (рис. 155). Составьте соответствующую таблицу. Выясните состояние производства электроэнергии в этих же странах в 1995, 2000, 2005 годах. Поместите их в таблицу и на основе этих данных постройте столбчатые диаграммы.
Постройте столбчатые диаграммы по данным (в тыс. человек) о количестве жителей крупнейших городов Украины (2001 г.):
Киев — 2629; Донецк — 1042;
Харьков — 1490; Днепропетровск — 1094;
Одесса — 1002; Запорожье — 840.
4.6. СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ ВЕРОЯТНОСТИ
Построением и исследованием моделей различных процессов, связанных с понятием случайности, занимаются математическая статистика и теория вероятностей. К таким процессам, например, относятся риски (рискованные операции) на производстве и в банковском деле, массовые заболевания среди растений, животных или людей, азартные игры.
Из предыдущих классов вы уже имеете некоторые представления о теории вероятностей, теперь немного расширим и углубим их.
Важнейшими понятиями теории вероятностей являются вероятностный эксперимент (испытание, наблюдение), событие (следствие испытания) и вероятность события. Приведём примеры испытаний и их отдельных последствий — некоторых событий.
Испытание Событие
1 Падает монета Упала вверх гербом
2 Играют команды А и С Выиграла команда С
3 Человек ждет весну Весна наступила
4 Падает игральный кубик Выпало 0 очков
Последнее событие невозможное, поскольку на гранях игрального кубика нет нуля. Событие 3 достоверное, так как после зимы всегда наступает весна. События 1 и 2 случайные.
Вообще, событие называется невозможным, если оно никогда не может произойти, достоверным — если оно всегда происходит. Если событие может произойти или не произойти, его называют случайным.
Принято считать, что невозможное и достоверное события — частные случаи случайного события.
События обозначают большими латинскими буквами А, В, С,... , или одной латинской буквой с индексом: Содержание события подают в фигурных скобках. Например, третье событие из таблицы можно записать так:
= {весна наступила}.
Сказать заранее о случайном событии, что оно состоится или не состоится, нельзя. Если же это событие массовое, выполняется много раз и при одинаковых условиях, то вероятность его наступления можно характеризовать некоторым числом.
Это можно сделать тогда, когда последствия испытаний равновозможные и составляют конечное множество, т.е. в условиях проведённого испытания нет оснований считать появление одного из следствий более или менее возможным, чем других.
Рассмотрим пример. Бросают один раз правильный однородный игорный кубик (рис. 159) и фиксируют количество очков на грани, оказавшейся вверху. Результатом такого испытания могут стать 6 различных событий:
={выпадает одно очко};
{выпадет два очка};
= {выпадет три очка};
= {выпадет четыре очка};
={ {выпадет пять очков};
= {выпадет шесть очков}.
Эти шесть событий охватывают и исчерпывают все возможные последствия эксперимента. Они попарно несовместимы, ибо каждый раз выпадает только одно количество очков. Все шесть событий одинаково возможны, поскольку речь идёт об однородном кубике правильной формы и ловкость игрока исключается. В таком случае говорят, что для осуществления каждого из этих событий существует один шанс из шести.
Каждое из событий -
вышеописанного испытания называют элементарным, а всё их множество — пространством элементарных событий.
Элементарным событием называют каждый возможный результат вероятностного эксперимента. Множество всех возможных последствий эксперимента называют пространством элементарных событий и обозначают греческой буквой Ω (омега).
Если пространство элементарных событий для некоторого испытания состоит из n равновозможных несовместимых событий, то вероятность каждого из них равна . Например, вероятность того, что на подброшенном игорном кубике выпадет 5 очков, равна
. А вероятность того, что подброшенная монета
упадёт вверх гербом, равна . Вероятность события А обозначают Р(А). Если первое из этих событий обозначить буквой А, а второе — буквой В, то Р(А) =
, Р(В) =
.
Есть события неэлементарные. Рассмотрим, например, такое событие:
С ={появление пластинки домино с 10 очками}.
Поскольку пластинок домино всего 28, то испытание, связанное с выбором одной пластинки, исчерпывается 28 равновозможными и независимыми последствиями. Следовательно, пространство элементарных событий для данного испытания состоит из 28 элементарных событий i=1,2, … ,28. Событие С может произойти, если произойдёт одно из двух элементарных событий :
= {появление пластинки
};
2)= {появление пластинки
}.
Говорят, что событию С способствуют два элементарных
события () из возможных 28, поэтому Р(С) =
=
.
Рассмотрим общий случай. Пусть испытание имеет конечное количество (n) равновозможных и несовместимых последствий и А — некоторое случайное событие, связанное с данным испытанием.
Будем называть элементарное событие благоприятным для случайного события А, если наступление события
в результате испытания приводит к наступлению события А.
Если количество последствий (элементарных событий), благоприятных событию Л, обозначить через n(А), то вероятность случайного события А определяется по формуле: P(A)=.
Вероятностью случайного события А называют отношение числа n(А) благоприятных для события А элементарных событий к числу n всех равновозможных и попарно несовместимых элементарных событий, которые образуют пространство элементарных событий для данного испытания.
Такое определение вероятности называют классическим.
Перечислим важнейшие свойства вероятности случайного события.
Если С — событие невозможное, то Р(С) = 0.
Если В — событие достоверное, то Р(В) = 1.
Если X — событие случайное, то 0≤Р(Х) ≤ 1.
Если - элементарные события, исчерпывающие некоторое испытание, то Р(
) + Р(
) + ...+ Р(
) = 1.
1. Какова вероятность того, что при падении игрального кубика выпадет:
а) два очка; б) чётное число очков; в) число очков, кратное 3?
2. Из перевёрнутых 28 костяшек домино наугад берут одну.
Какова вероятность того, что на ней окажется всего: а) 2 очка (событие А); б) 5 очков (событие В); в) 12 очков (событие С)?
Из перевёрнутых 28 костяшек домино наугад берут одну. Какова вероятность того, что на одной из её частей окажется 6 очков
(событие А)?
4. Окрашенный со всех сторон деревянный кубик распилили на 64 равных кубика и поместили их в коробку. Какова вероятность того, что в кубике, вынутом наугад из коробки, будет окрашено: а) только одну грань; б) ровно две грани; в) не менее трёх граней?
5. Окрашенный со всех сторон деревянный кубик распилили на 125 равных кубиков и поместили их в мешок. Какова вероятность того, что вынимая из мешка кубик наугад, вы возьмёте такой, у которого окрашено: а) только одну грань; б) только две грани; в) три грани?
6. Из букв, написанных на отдельных карточках, составили слово МАТЕМАТИКА, потом эти карточки перевернули, перетасовали и взяли наугад одну из них. Какова вероятность того, что на ней окажется: а) буква А; б) буква Ml
7. В кульке есть 20 свёрнутых бумажек. На двух из них написано «нет», а на остальных — «да». Какова вероятность того, что на взятой наугад бумажке окажется слово «да»?
8. В группе, кроме А, В, С, есть ещё 12 учеников. Какова вероятность того, что выбранная группой делегация из трёх человек будет состоять из учеников А, В и С?
9. В группе, кроме вас, есть ещё 12 учеников. Какова вероятность того, что в избранную группой делегацию из трёх человек войдёте и вы?
4.7. ОТНОСИТЕЛЬНАЯ ЧАСТОТА СОБЫТИЯ И СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
До сих пор речь шла о классическом понимании вероятности. Её вычисляют, исходя из того, что все рассматриваемые элементарные события одинаково вероятны. Такое случается сравнительно редко.
Представьте, что игральный кубик сделан так, что его грань с шестью очками находится дальше от центра масс, чем противоположная грань. Такой кубик и падает чаще вверх гранью с 6 очками. При этом наблюдается интересная и очень важная законо
мерность. Когда кто-то один подбросил такой кубик 1000 раз и он упал, например, 300 раз вверх гранью с 6-ю очками, то и другие экспериментаторы имели бы примерно такие же результаты. Много массовых случайных событий имеют свойство устойчивости. При достаточно большом числе независимых испытаний частота появления наблюдаемого события колеблется около одного и того же числа. В справедливости этого многие специалисты убедились экспериментально. А математики Я. Бернулли, П. Чебышев и др. обосновали это утверждение и теоретически (закон больших чисел). Поэтому для таких (статистически устойчивых) событий есть смысл ввести понятие вероятности.
Если в n испытаниях событие А происходит m раз, то дробь
определяет относительную частоту события А. Во многих реальных случаях с увеличением n относительная частота событий стабилизируется и всё меньше отличается от некоторого числа р (когда n→∞, то
→р). Это число р называют вероятностью события А.
Таково статистическое определение вероятности. Объём определённого им понятия гораздо шире того, что соответствует классическому определению (см. с. 314). Классическая вероятность — отдельный вид статистической. И всё же отличаются они существенно. Классическую вероятность вычисляют математическими методами, а статистическую в основном определяют экспериментально.
Теперь, говоря о вероятности, специалисты в основном подразумевают статистическую вероятность. Поэтому современная теория вероятностей тесно связана с математической статистикой. Объединение математической статистики и теории вероятностей называют стохастикой. Стохастический — значит случайный, вероятный.
Что такое экзит-пол? На каких основаниях ему доверяют? Экзит-пол — это опрос социологическими службами избирателей на выходе их из избирательных участков с целью предсказать результаты выборов до получения их от избирательных комиссий. Ему доверяют на основе устойчивости относительной частоты события. Если за какую-то партию или кандидата из правильно выбранных 100 избирателей проголосовали, например, 20 % избирателей участка, то можно надеяться (с погрешностью около 5 %), что так проголосовали и все избиратели участка.
Одно из важнейших понятий стохастики — случайная величина. Величину называют случайной, если она может принимать заранее неизвестные числовые значения, зависящие от случайных обстоятельств. Примеры:
1)выигрыш на лотерейный билет;
2)расстояние от точки попадания пули к центру мишени.
Значение первой из этих случайных величин — некоторые целые числа. Такие величины называют дискретными. Множество значений второй величины — некоторый непрерывный отрезок числовой прямой. Такие величины называют непрерывными.
Рассмотрим задачу. Выпущено 100 лотерейных билетов. Из них 5 должны выиграть по 10 грн, 10 — по 5 грн, 40 — по 1 грн, остальные — безвыигрышные. Какой средний выигрыш приходится на один билет?
Решить эту задачу можно арифметическим способом:
(5 • 10 грн + 10-5 грн + 40 • 1 грн): 100 = 1,4 грн.
Мы проиллюстрируем на этой задаче понятие случайной величины. Здесь выигрыш — случайная величина, которая может принимать значения 0, 1, 5, 10 (грн) соответственно с вероятностями 0,45;0,4;0,1и 0,05. Это — дискретная случайная величина Описанной ситуации соответствует такая таблица:
ξ 0 1 5 10
p 0,45 0,4 0,1 0,05
Обратите внимание! Сумма вероятностей, имеющихся во второй строке таблицы, равна 1. Говорят, что данную случайную величину ξ распределено по вероятностям.
Если случайная величина ξ принимает значения с вероятностями соответственно
то говорят, что величину ξ , распределено по такому закону:
ξ
p
Её среднее значение называют математическим ожиданием и обозначают М(ξ ).
М(ξ ) =
Например, для предыдущей задачи
М(ξ ) = 0 ∙ 0,45 + 1∙ 0,4 + 5 ∙ 0,1 + 10 ∙ 0,05 = 1,4.
Меру рассеиваний случайной величины вокруг её математического ожидания называют её дисперсией. Дисперсию случайной величины х обозначают символом D(x) и вычисляют по формуле D(x) = Здесь Мх — математическое ожидание величины х,
— квадраты отклонений значений х от Мх. Величина
также случайная, её математическое ожидание
— дисперсия случайной величины х.
Например, чтобы найти дисперсию рассмотренной выше случайной величины сначала найдём отклонения всех её значений от математического ожидания:
О - 1,4 = -1,4; 1 - 1,4=-0,4; 5 - 1,4 = 3,6; 10 - 1,4 = 8,6.
Квадраты этих отклонений: 1,96, 0,16, 12,96, 73,96. Найдём математическое ожидание случайной величины:
1.96 0.16 12.96 73.96
p 0.45 0.4 0.1 0.05
1,96 ∙ 0,45 + 0,16 ∙ 0,4 + 12,96 ∙ 0,1 + 73,96 ∙ 0,05 = 5,94.
Это и есть дисперсия рассматриваемой случайной величины: D(ξ)=5.96 .
Если случайная величина дискретная и вероятности всех её шачений равны, то говорят, что она имеет равномерное дискретное распределение вероятностей. По равномерному распределению выпадает число очков при подбрасывании правильного игрального кубика. А бывают другие распределения.
Для многих природных и общественных явлений характерны биномиальные распределения вероятностей. Биномиальное распределение возникает при последовательном проведении в одинаковых независимых условиях случайных опытов.
Английский математик А. Муавр ещё в XVIII в. измерил рост 1375 наугад выбранных женщин. На рисунке 164 изображена диаграмма, которая соответствует результатам его измерений. Если «успехом» назвать тот факт, что следующая встреченная женщина имеет рост, который находится в определённых пределах, то число женщин такой категории среди 1375 встреченных является случайной величиной с биномиальным распределением. Относительно параметра р можно утверждать, что этим числом может служить относительная частота женщин выделенной категории роста, поскольку число проведённых опытов достаточно большое и эта частота стабилизировалась. Английский
психолог Ф. Гальтон сконструировал прибор (доску Гальтона), который наглядно показывает, как формируется случайная величина, распределённая по биномиальному закону, правда при
р = (рис. 165). В верхний резервуар насыпаются шарики.
Скатываясь по наклонной доске и обходя равномерно забитые в неё колышки, шарики заполняют нижние ячейки согласно биномиальному распределению вероятностей.
Если шариков достаточно много, то внизу они образуют симметричную горку колоколообразной формы. Верхний предел этой горки образует полигон, который при росте числа шариков приближается к кривой Гаусса — так называемой кривой плотности стандартного нормального закона.
В рассмотренном выше примере результаты измерения роста-
женщин разбиты на 18 групп с разностью d = 2,5 см. Если бы разошли их на большее количество групп, чтобы эта разность равнялась, например, 0,5 см, и построили соответствующий полигон, то образовалась бы ломаная из многих отрезков. А если бы разность d продолжали уменьшать, то соответствующий полигон приближался бы к непрерывной кривой, изображённой на рисунке 164. Это — кривая плотности нормального распределения вероятностей. Примерно так распределяются вероятности масс новорождённых, скоростей газовых молекул и многих других случайных величин физической, биологической или социальной природы. Биномиальное распределение характерно для многих дискретных случайных величин, а нормальное — для непрерывных. Если известно, что распределение вероятностей случайной величины нормальное, то достаточно знать только две её числовые характеристики (математическое ожидание и дисперсию), чтобы полностью описать распределение вероятностей.
Понимание сути нормального распределения необходимо всем учёным, исследующим закономерности живой или неживой природы и особенно — человеческого общества. Не случайно это распределение называют нормальным, оно — естественное. Именно так чаще всего распределяются не только массы, возрасты, физические возможности людей и человеческих сообществ, но и многие другие их характеристики. Не понимая этого, нельзя быть настоящим учёным.
Задачи.
Известно, что среди 1000 новорождённых обычно бывает 511 мальчиков и 489 девочек. Найдите вероятность рождения мальчика.
Распределите по вероятностям случайную величину количества очков, выпадающих при бросании правильного игрального кубика. Найдите математическое ожидание этой случайной величины.
Только одна грань правильного однородного кубика окрашена жёлтым цветом. С какой относительной частотой будет падать этот кубик вверх жёлтой гранью, если его бросать много раз?
На гранях правильного октаэдра нанесены очки от 1 до 8. Задайте таблицей случайную величину количества очков, выпадающих при бросании такого тетраэдра. Найдите среднее значение этой величины.
Выпущено 1000 лотерейных билетов, на один из которых должен выпасть выигрыш 100 грн, на 10- по 20 грн, на 50- по 1 грн. Задайте таблицей математическое ожидание этой величины.
Раздел 2. Олимпиадные задачи по комбинаторике и теории вероятностей.
2.1 5 класс.
1. В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
Решение:
Выберем чашку. В комплект к ней можно выбрать любое из трех блюдец. Поэтому есть 3 разных комплекта, содержащих выбранную чашку. Поскольку чашек всего 5, то число различных комплектов равно 15 (15 = 5 • 3).
2. В магазине «Все для чая» продается 5 чашек, 3 блюдца и 4 чайные ложки. Сколькими способами можно купить два предмета с разными названиями?
Решение:
Возможны три разных случая: первый – покупаются чашка с блюдцем, второй – чашка с ложкой, третий – блюдце и ложка. В каждом из этих случаев легко сосчитать количество возможных вариантов (в первом – 15, во втором – 20, в третьем – 12). Складывая, получаем общее число возможных вариантов: 47.
3. В Стране Чудес есть четыре города: А, Б и В и Г. Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги, Из города А в город Г – две дороги, и из города Г в город В – тоже две дороги. Сколькими способами можно проехать от А до В?
Решение:
Выделим два случая: путь проходит через город Б или через город Г. В каждом из этих случаев легко сосчитать количество возможных маршрутов: в первом – 24, во втором – 6. Складывая, получаем общее количество маршрутов: 30
4. Назовем натуральное число «симпатичным» , если в его записи встречаются только нечетные цифры. Сколько существует 4-значных «симпатичных» чисел?
Решение:
Понятно, что однозначных «симпатичных» чисел ровно 5. К каждому однозначному «симпатичному» числу вторая нечетная цифра может быть дописана пятью различными способами. Таким образом, двузначных «симпатичных» чисел всего 5 • 5 = 25. Аналогично, трехзначных «симпатичных» чисел 5 • 5 • 5 = 125, и четырехзначных – 5 • 5 • 5 • 5 = 54 = 625.
5. В ящике лежат шары: 5 красных, 7 синих и 1 зелёный.
Сколько шаров надо вынуть, чтобы достать два шара одного цвета?
Решение :
1 зеленый+1 красный+1синий=3-неблагоприятный исход. Добавив 1 шар всегда получится 2 шара одного цвета.
Ответ: надо вынуть 4 шара.
2.2 6 класс.
1. Назовем натуральное число «симпатичным» , если в его записи встречаются только нечетные цифры. Сколько существует 4-значных «симпатичных» чисел?
Решение:
Понятно, что однозначных «симпатичных» чисел ровно 5. К каждому однозначному «симпатичному» числу вторая нечетная цифра может быть дописана пятью различными способами. Таким образом, двузначных «симпатичных» чисел всего 5 • 5 = 25. Аналогично, трехзначных «симпатичных» чисел 5 • 5 • 5 = 125, и четырехзначных – 5 • 5 • 5 • 5 = 54 = 625.
2. В ящике находятся разноцветные шарики: 5 белых, 12 красных и 20 черных. Какое наименьшее число шариков нужно достать из ящика, чтобы среди них обязательно было хотя бы по одному шарику всех цветов?
Решение:
С учетом неблагоприятного исхода: 20+12+1=33.
Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение:
На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 • 3 • 2 • 1 = 4!.
Сколько существует трехзначных чисел, в записи которых цифры 1, 2, 3 встречаются ровно по одному разу?
Решение:
Будем рассуждать точно так же, как при решении задач предыдущего цикла. На первое место можно поставить любую из трех цифр, на второе – любую из двух оставшихся, а на третье – последнюю оставшуюся цифру. Таким образом, всего получается 3 • 2 • 1 = 3! чисел.
2.3 7 класс.
1. В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Решение:
Капитаном может стать любой из 11 футболистов. После выбора капитана на роль его заместителя могут претендовать 10 оставшихся человек. Таким образом, всего есть 11 • 10 = 110 разных вариантов выборов.
2. Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя шести различных цветов?
Решение:
Цвет для верхней полоски флага можно выбрать шестью разными способами. После этого для средней полоски флага остается пять возможных цветов, а затем для нижней полоски флага – четыре различных цвета. Таким образом, флаг можно сделать 6 • 5 • 4 = 120 способами.
3. На доске написаны 7 существительных, 5 глаголов и 2 прилагательных. Для предложения нужно выбрать по одному слову каждой из этих частей речи. Сколькими способами это можно сделать?
Решение:
Ответ: 7 • 5 • 2 = 70
4. Можно ли покрыть равносторонний треугольник двумя равносторонними треугольниками меньшего размера?
Решение:
Каждый из меньших треугольников может покрыть только одну вершину большего, но вершин три, а треугольников только два.
Ответ: нельзя.
5. Из пяти данных окружностей любые четыре проходят через одну точку. Докажите, что найдётся точка, через которую проходят все пять окружностей.
Решение:
Пусть 1-я, 2-я, 4-я и 5-я окружности проходят через точку А; 1-я, 3-я, 4-я и 5-я – через точку В; 2-я, 3-я, 4-я и 5-я – через точку С.
Мы видим, что все три точки А, В и С не могут быть различными, так как они лежат на 4-й и 5-й окружностях, а две окружности имеют не больше двух точек пересечения. Значит, согласно принципу Дирихле, какие-то две из точек А, В и С совпадают.
Пусть, например, совпадают точки А и В. Тогда все окружности проходят через точку А. Доказательство завершено.
2.4 8 класс.
1. Сколькими способами можно поставить на шахматную доску белую и черную ладьи так, чтобы они не били друг друга?
Решение:
Белую ладью можно поставить на любую из 64 клеток. Независимо от своего расположения она бьет 15 полей (включая поле, на котором она стоит). Поэтому остается 49 полей, на которые можно поставить черную ладью. Таким образом, всего есть 64 • 49 = 3136 разных способов.
2. Непересекающиеся треугольники.
Из вершин правильного n-угольника (n5) наугад выбираются две тройки различных точек. Какова вероятность того, что два треугольника, вершинами которых являются выбранные тройки, не пересекаются?
Решение:
Разобьем все возможные пары троек вершин на Сn6 групп, собирая в одной группе те и только те пары троек, которые образуют одинаковые шестерки вершин. С одной стороны, каждая такая группа содержит столько элементов, сколькими способами можно разбить шестерку фиксированных вершин на две тройки, то есть С63 = 20 элементов. С другой стороны, существует ровно 6 способов разбить шестерку на две тройки, удовлетворяющие требуемому в задаче условию. Поэтому искомая вероятность равна 6/20 = 0,3.
Ответ: 0,3.
Белые и чёрные шары.
Каждая из двух урн содержит белые и чёрные шары, причём общее число шаров в обеих урнах равно 25. Из каждой урны наугад вынимают по одному шару. Зная, что вероятность того, что оба вынутых шара окажутся белыми, равна 0,54, найдите вероятность того, что оба вынутых шара окажутся чёрными.
Решение:
Пусть общее количество шаров в первой и второй урнах равно m1 и m2 соответственно (для определенности считаем, что m1 не больше m2), а количество белых шаров в этих урнах равно k1 и k2соответственно. Тогда вероятность того, что оба вынутых шара белые, равна ( k1/m1)·( k2/m2).
Получаем соотношения: ( k1/m1)·( k2/m2) = 0,54 = 27/50, m1 + m2 = 25.
Так как 27m1m2 = 50k1k2, то хотя бы одно из чисел m1, m2 делится на 5. Но сумма m1 + m2 тоже делится на 5, поэтому каждое из чисел m1, m2 делится на 5. Таким образом, имеем всего две возможности: либо m1 = 5, m2 = 20,либо m1 = 10, m2 = 15.
В случае m1 = 5, m2 = 20 получаем k1k2 = 54, где k1 не превосходит 5, а k2 не превосходит 20. Перебрав все возможные значения ki, найдем k1=3, k2=18. Тогда в первой урне 2 черных шара, во второй тоже 2 черных шара, и вероятность вытащить два черных шара равна (2/5)·(2/20)=0,04.
Аналогично, в случае m1 = 10, m2 = 15 находим k1= 9, k2=9. Тогда в первой урне 1 черный шар, во второй – 6 черных шаров, и вероятность вытащить два черных шара равна (1/10)·(6/15) = 0,04 (в обоих случаях ответы одинаковы).
Ответ: 0,04.
Орёл или решка?
Два игрока А и В наблюдают за мальчиком, который без остановки подбрасывает монету. Результаты подбрасываний записываются последовательно с помощью букв: на k-м месте последовательности ставится буква О или буква Р в зависимости от того, что выпадает при k-м подбрасывании – «орёл» или «решка» соответственно. Игрок А утверждает, что тройка ООО встретится в записи раньше, чем тройка ОРО. Игрок В поспорил, что произойдет обратное. Кто из игроков имеет больше шансов выиграть в этом споре?
Решение:
За первой буквой О (с момента начала наблюдения за мальчиком с вероятностью 1 буква О хотя бы один раз появится) с одинаковой вероятностью, равной 1/4, может следовать одна из комбинаций: РО, ОО, РР, ОР.
В первом случае выигрывает игрок В, во втором случае выигрывает игрок А, а если реализовался третий случай, то после этого игроки будут иметь такие же шансы, как и в начале игры. В четвертом случае с вероятностью 1/2 последует буква О и выиграет игрок В, а с вероятностью 1/2 последует буква Р, после чего игроки будут иметь такие же шансы, как и в начале игры. Таким образом, с вероятностью 1/4 выиграет А, с вероятностью 1/4 + 1/4 · 1/2 = 3/8
выиграет В и с вероятностью 3/8 возникнет ситуация, когда игроки будут иметь такие же шансы, как в начале игры. Поэтому игрок В имеет больше шансов выиграть, чем игрок А.
Ответ: игрок В.
5. В одной из популярных в Америке игр игрок бросает монету с достаточно большого расстояния на поверхность стола, разграфленную на однодюймовые квадраты. Если монета (3/4 дюйма в диаметре) попадает полностью внутрь квадрата, то игрок получает награду, в противном случае он теряет свою монету. Каковы шансы выиграть при условии, что монета упала на стол?
Решение:
Когда мы бросаем монету на стол, то некоторые области положения центра тяжести монеты вероятнее других, но если квадрат достаточно мал, можно считать, что распределение вероятностей равномерно. Это означает, что вероятность попадания центра в какую-либо область квадрата пропорциональна площади этой области; она равна площади области, деленной на площадь квадрата. Так как радиус монеты равен 3/8 дюйма, то для выигрыша игрока центр не должен находиться ближе, чем 3/8 дюйма от сторон квадрата
Этому ограничению отвечает квадрат со стороной 1/4 дюйма, внутри которого должен лежать центр монеты. Так как вероятности пропорциональны площадям, то вероятность выигрыша равна (1/4)2 = 1/16.
Разумеется, монета вообще может не попасть на стол, и вероятность выигрыша на самом деле еще меньше. Квадраты также могут быть уменьшены за счет утолщения разделяющих линий. Если эти линии имеют толщину и 1/16 дюйма, то выигрышной области соответствует вероятность (3/16)2 = 9/256, или меньше 1/28.
Ответ: 1/16.
2.5 9 класс.
1. В плоскости дано конечное множество многоугольников, каждые два из которых имеют общую точку. Докажите, что некоторая прямая пересекает все эти многоугольники.
Решение:
Спроектируем все многоугольники на некоторую прямую. Проекция каждого многоугольника является отрезком, причём по условию любые два отрезка имеют общую точку. Отсюда следует, что все отрезки имеют общую точку (чтобы убедиться в этом, достаточно рассмотреть данную прямую как числовую ось и взять наименьший из правых концов этих отрезков). Прямая, перпендикулярная к данной и проходящая через отмеченную точку, пересекает все многоугольники.
2. Имеется несколько квадратов, сумма площадей которых равна 4. Докажите, что такими квадратами всегда можно покрыть квадрат площади 1.
Решение:
Если покрывать квадрат набором квадратов, сторона каждого из которых уменьшена до ближайшего меньшего числа вида 1/2k, k = 1, 2, ... , то эти квадраты можно разместить без наложений (смотрите рисунок).
Поскольку площадь каждого квадрата уменьшилась менее чем в 4 раза, то сумма их площадей больше 1, так что они заведомо покроют весь квадрат.
Подбрасывание монеты.
Игрок А бросает монету n+1 раз, а игрок В – n раз. Какова вероятность того, что в итоге у игрока А выпадет больше «орлов», чем у игрока В?
Решение:
Пусть у игроков А и В выпадает m и k «орлов» соответственно. Тогда искомая вероятность р события mk равна вероятности q события
(n + 1) – m n – k,
то есть вероятности того, что у игрока А выпадает больше «решек», чем у игрока В (так как при каждом бросании монеты «орел» и «решка» выпадают с равной вероятностью).
С другой стороны, событие mk имеет место тогда и только тогда, когда
n – m
то есть когда (n+1)–m не превосходит n–k (поскольку n–m и n–k – целые числа). Поэтому р=1–q, откуда имеем p=q=1/2.
Ответ: 1/2.
4. Сколько существует 6-значных чисел, в записи которых есть хотя бы одна четная цифра?
Решение:
Вместо того, чтобы подсчитывать количество требуемых 6-значных чисел, определим количество 6-значных чисел, не обладающих нужным свойством. Так как это в точности те числа, в записи которых встречаются только нечетные цифры, то их количество, очевидно, равно 56 = 15625. Всего 6-значных чисел 900000. Поэтому количество 6-значных чисел, обладающих указанным свойством, равно 900000 – 15625=884375.
5. На какое наименьшее число неперекрывающихся тетраэдров можно разбить куб?
Решение:
Легко видеть, что куб можно разбить на 5 тетраэдров. На рисунке это тетраэдры АА'В'D', АВ'ВС, АСDD', В'С'D'С и АСD'В'.
Докажем теперь, что на меньшее число тетраэдров разбить куб нельзя. Пусть куб с ребром а разбит на несколько тетраэдров. Имеются, по крайней мере, два из них, основания которых лежат на грани АВСD куба. Точно так же имеются по крайней мере 2 тетраэдра с основаниями на грани А'В'С'D'.
Эти тетраэдры заведомо отличны от первых двух, так как у тетраэдра не может быть двух параллельных граней. Итак, у нас уже есть 4 тетраэдра. Их общий объем не больше чем 2а3/3, то есть меньше объёма куба. Таким образом, на 4 тетраэдра куб разбить нельзя.
Ответ: 5.
2.6 10 класс.
Сколькими способами можно поставить на шахматную доску белого и черного королей так, чтобы получилась допустимая правилами игры позиция?
Решение:
Белого короля можно поставить на любое из 64 полей. Однако количество полей, которые он при этом будет бить, зависит от его расположения. Поэтому необходимо разобрать три случая:
а) если белый король стоит в углу (углов всего 4), то он бьет 4 поля (включая то, на котором стоит), и остается 60 полей, на которые можно поставить черного короля;
б) если белый король стоит на краю доски, но не в углу (таких полей – 24), то он бьет 6 полей, и для черного короля остается 58 возможных полей;
в) если же белый король стоит не на краю доски (таких полей – 36), то он бьет 9 полей, и для черного короля остается 55 возможных полей.
Таким образом, всего есть 4 • 60 + 24 • 58 + 36 • 55 = 3612 способов расстановки королей.
В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?
Решение:
Каждая авиалиния соединяет два города. В качестве первого города можно взять любой из 20 городов (город А), а в качестве второго – любой из 19 оставшихся (город В). Перемножив эти числа, получаем 20 • 19 = 380. Однако при этом подсчете каждая авиалиния учтена дважды (первый раз, когда в качестве первого города был выбран город А, а второго – город В, а второй раз – наоборот). Таким образом, число авиалиний равно 380:2 = 190.
Катящаяся игральная кость.
Обычная игральная кость имеет на своих гранях числа 1, 2, 3, 4, 5, 6. Ее бросают случайным образом до тех пор, пока сумма выпавших за время бросания очков не превысит числа 12. Какая общая сумма очков будет наиболее вероятной?
Решение:
Рассмотрим предпоследний бросок. После него общая сумма должна принимать одно из следующих значений: 12, 11, 10, 9, 8, 7. Если она равна 12, то общий результат будет с равной вероятностью принимать значения 13, 14, 15, 16, 17, 18. Аналогично, при сумме 11 конечный результат с равной вероятностью принимает значения 13, 14, 15, 16, 17 и так далее. Число 13 появляется как равный кандидат в каждом случае и является единственным числом такого рода. Таким образом, число 13 – наиболее вероятное.
В общем те же доводы показывают, что наиболее вероятная сумма, впервые превышающая n (n равно 6 и более), есть n+1.
Ответ: 13.
Подбрасывание монеты.
Игрок А бросает монету n+1 раз, а игрок В – n раз. Какова вероятность того, что в итоге у игрока А выпадет больше «орлов», чем у игрока В?
Решение:
Пусть у игроков А и В выпадает m и k «орлов» соответственно. Тогда искомая вероятность р события mk равна вероятности q события
(n + 1) – m n – k,
то есть вероятности того, что у игрока А выпадает больше «решек», чем у игрока В (так как при каждом бросании монеты «орел» и «решка» выпадают с равной вероятностью).
С другой стороны, событие mk имеет место тогда и только тогда, когда
n – m
то есть когда (n+1)–m не превосходит n–k (поскольку n–m и n–k – целые числа). Поэтому р=1–q, откуда имеем p=q=1/2.
Ответ: 1/2.
Трёхсторонняя дуэль.
Три стрелка А, В, С решили одновременно драться на дуэли. Они расположились в вершинах равностороннего треугольника и условились о следующем: первый выстрел делает А, второй – В, третий – С и так далее по кругу; если один из стрелков выбывает, то дуэль продолжается между двумя оставшимися. Известно, что стрелок А поражает цель с вероятностью 0,3, стрелок С – с вероятностью 0,5, а стрелок В вообще никогда не промахивается. Каждый стреляет в одного из двух других или в воздух с таким расчетом, чтобы с наибольшей вероятностью выиграть дуэль. Куда должен направить свой первый выстрел стрелок А: в стрелка С, в стрелка В или в воздух?
Решение:
Рассмотрим три события, которые могут наступить после первого выстрела стрелка А.
Поражен С. Тогда с вероятностью 1 стрелок А будет поражен первым же выстрелом В.
Поражен В. Тогда:
или с вероятностью 0,5 стрелок С поразит А своим первым выстрелом,
или с вероятностью (1 – 0,5) · 0,3 стрелок А поразит С своим вторым выстрелом,
или с вероятностью (1 – 0,5) · (1 – 0,3) · 0,5 стрелок С поразит А своим вторым выстрелом,
или с вероятностью (1 – 0,5) · (1 – 0,3) · (1 – 0,5) · 0,3 стрелок А поразит С своим третьим выстрелом и так далее.
Следовательно, вероятность для А выиграть дуэль в этом случае равна
0,5 · 0,3 + 0,5 · 0,7 · 0,5 · 0,3 + 0,5 · 0,7 · 0,5 · 0,7 · 0,5 · 0,3 + . . . =
0,15 · (1 + 0,35 + 0,352 + . . .) = 0,15 · 1/(1 – 0,35) = (15/100) · (100/65) = 3/13.
3) Никто не поражен. После этого В будет стрелять в С (как в более меткого из своих противников) и поразит его. Затем А с вероятностью 0,3 поразит В, выиграв дуэль.
Таким образом, так как 0,3 3/13, то самой выгодной для стрелка А является ситуация, когда после его выстрела никто не поражен. Значит, он должен первый раз стрелять в воздух.
Ответ: А должен первый раз стрелять в воздух.
2.7. 11 класс.
1. Слово – любая конечная последовательность букв русского алфавита. Выясните, сколько различных слов сожно составить из слов
а) «ВЕКТОР»;
б) «ЛИНИЯ»;
в) «ПАРАБОЛА»;
г) «БИССЕКТРИСА»;
д) «МАТЕМАТИКА»;
Решение:
а) Так как все буквы слова различны, то всего можно получить 6! слов.
б) В этом слове две буквы И, а все остальные буквы разные. Временно будем считать разными и буквы И, обозначив их через И1 и И2. При этом предположении получится 5! = 120 разных слов. Однако те слова, которые получаются друг из друга только перестановкой букв И1 и И2, на самом деле одинаковы. Таким образом, полученные 120 слов разбиваются на пары одинаковых. Поэтому разных слов всего 120:2 = 60.
в) Считая три буквы А этого слова различными (А1, А2, А3), получим 8! разных слов. Однако слова, отличающиеся лишь перестановкой букв А, на самом деле одинаковы. Поскольку буквы А1, А2, А3 можно переставлять 3! способами, все 8! слов разбиваются на группы по 3! одинаковых. Поэтому разных слов всего 8!/3!.
г) В этом слове три буквы С и две буквы И. Считая все буквы различными, получаем 11! слов. Отождествляя слова, отличающиеся лишь перестановкой букв И, но не С, получаем 11!/2! различных слов. Отождествляя теперь слова,отличающиеся перестановкой букв С, получаем окончательный результат 11!/(2!•3!).
д) Ответ: 10!/(3! • 2! • 2!).
2. На окружности отмечено n точек. Сколько существует незамкнутых несамопересекающихся (n–1)-звенных ломаных с вершинами в этих точках?
Решение:
Первую точку можно выбрать n способами. Каждую из следующих n–2 точек можно выбрать двумя способами, так как она должна быть соседней с одной из ранее выбранных точек (иначе получится самопересекающаяся ломаная).
Поскольку начало и конец при таком подсчёте не различаются, результат нужно разделить на 2. Следовательно, всего имеется n·2n–2/2 = n·2n–3 ломаных.
Ответ: n·2n–3.
3. а) Выбраны шесть цветов, и требуется раскрасить шесть граней куба в разные цвета. Сколькими различными способами можно это сделать? (Различными считаются те раскраски, которые нельзя совместить одну с другой при помощи вращений куба вокруг его центра.)
б) Сколькими различными способами можно раскрасить грани додекаэдра в двенадцать цветов?
Решение:
a) Куб можно повернуть так, чтобы грань, окрашенная первым цветом, заняла заданное положение. Для окраски противоположной ей грани есть пять различных вариантов; разные раскраски противоположной грани дают различные раскраски куба.
Среди оставшихся четырёх граней можно выбрать грань, окрашенную данным цветом, и перевести её в данное положение (не меняя при этом положение первых двух граней). Разные раскраски трёх оставшихся граней дают различные раскраски куба. Одну из этих граней можно окрасить тремя способами, одну из оставшихся – двумя. Всего получаем 5 · 3 · 2 = 30 различных раскрасок.
Ответ: 30 способами.
б) Количество всех возможных раскрасок додекаэдра равно 12! = 1 · 2 · ... · 15. Чтобы найти число различных раскрасок, нужно поделить 12! на число самосовмещений додекаэдра. Любую из 12 граней можно перевести в любую другую. Кроме того, есть пять поворотов (включая тождественный), сохраняющих данную грань. Всего получается 60 самосовмещений. Поэтому количество различных раскрасок додекаэдра равно 12! / 60 = 7983360.
Ответ: 7983360 способами.
4. Каждая точка плоскости окрашена в красный или голубой цвет. Докажите, что найдется прямоугольник, все вершины которого окрашены в один и тот же цвет.
Решение:
Согласно принципу Дирихле, из семи точек не меньше четырёх должны иметь одинаковый цвет. Выберем из семи точек на прямой p четыре точки Р1, Р2, Р3, Р4, окрашенные в один цвет, скажем, в красный. Рассмотрим ещё две прямые q и r, параллельные прямой р, и две четверки точек на них (Q1, Q2, Q3, Q4) и (R1, R2, R3, R4), полученные ортогональным проектированием выбранной четвёрки на эти прямые. Рассмотрим прямоугольники с вершинами в этих точках и в точках Р1, Р2, Р3, Р4. Теперь, если две из точек, например, Qi и Qj – красные, то все точки прямоугольника РiQiQjРj также красные. Аналогично и для двух красных точек из R1, R2, R3, R4.
Если ни один из этих случаев не имеет места, то некоторые три (или более) точек на прямой q и три (или более) точек на прямой r должны быть голубыми. Но эти тройки голубых точек расположены так, что среди них обязательно найдутся по паре точек, лежащих одна под другой и, таким образом, образующие голубой прямоугольник, откуда и следует утверждение задачи.
Замечание: отметим, что этот результат справедлив для любой области на плоскости, заключённой внутри сколь угодно малой окружности.
5. Через фиксированную точку пространства проводим плоскости так, чтобы разделить пространство на возможно большее число частей. Одна плоскость разделит пространство на две части, две пересекающиеся плоскости – на четыре части, три пересекающиеся в некоторой точке плоскости и не имеющие другой общей точки делят пространство на восемь частей.
а) Какое максимальное число частей можно получить при четырех плоскостях?
б) Какое – при n плоскостях?
Решение:
Вместо всего пространства будем делить шар, через центр которого проводим плоскости. На поверхности шара (на ограничивающей его сфере) возникнут взаимно пересекающиеся большие окружности. Примем одну из них за экватор и все эти окружности спроектируем из центра шара на плоскость, касательную к шару в полюсе. Проекциями наших окружностей (за исключением одной, являющейся экватором и вовсе ни во что не проектирующейся) будут прямые. Следовательно, нужно вычислить максимальное число областей плоскости, разделенной n–1 прямыми. Методом индукции можно получить, что оно равно
1 + 1 + 2 + 3 + . . . + (n–1) = 1 + n(n–1)/2.
Так как на сфере имеется вдвое больше областей, чем на её плоской проекции (помним об экваторе, который присутствует на сфере и отсутствует на плоскости проекции), то искомое число будет вдвое больше вычисленного нами выше, следовательно, оно равно 2 + n(n–1).
В частности, при n = 4 искомым числом является 14.
Ответ: а) 14; б) 2+n(n–1).
6. Необходимо разделить треугольник на 19 треугольников так, чтобы в каждой вершине полученной фигуры (а также в вершинах большого треугольника) сходилось одинаковое число сторон. Число 19 нельзя заменить большим числом, но можно заменить меньшими числами. Какими же?
Решение:
Чтобы разделить треугольник на некоторое число треугольников так, чтобы в каждой вершине образованной фигуры сходилось одинаковое число сторон, воспользуемся правильными многогранниками, грани которых являются треугольниками. Это могут быть следующие многогранники: правильные тетраэдр, октаэдр и икосаэдр, и только они.
Если внутри тетраэдра мы выберем точку, лежащую близко от центра одной из граней, и из этой точки спроектируем рёбра тетраэдра на плоскость, то получим первую фигуру, изображенную на следующем рисунке.
Она состоит из трех треугольников, соответствующих граням тетраэдра; четвертая грань при проектировании перешла в большой треугольник ABC. В каждой вершине фигуры сходятся три стороны, так как в каждой вершине тетраэдра сходятся три ребра.
Подобным же образом, при помощи центральной проекции, получим из правильного октаэдра вторую фигуру на рисунке, состоящую из семи треугольников, в каждой вершине которой сходится четыре стороны, а из правильного икосаэдра – третью фигуру, состоящую из 19 треугольников, в каждой вершине которой сходится пять сторон.
Не существует фигуры, отвечающей условиям задачи и отличающейся от изображенных трёх, так как ей соответствовал бы правильный многогранник, отличающийся от трёх упомянутых выше, а такого не существует.
Итак, возможное число треугольников, меньшее 19 – это 4 и 7.
7. Легкомысленный член жюри.
В жюри из трех человек два члена независимо друг от друга принимают правильное решение с вероятностью p, а третий для вынесения решения бросает монету (окончательное решение выносится большинством голосов). Жюри из одного человека выносит справедливое решение с вероятностью p. Какое из этих жюри выносит справедливое решение с большей вероятностью?
Решение:
Два серьезных члена жюри будут голосовать за справедливое решение с вероятностью p·p = p2, при этом результат голосования третьего члена жюри не существен. Если же эти судьи расходятся во мнениях, вероятность чего равна
p · (1 – p) + (1 – p) · p = 2p · (1–p),
то для нахождения вероятности правильного решения это число надо умножить на 1/2. Таким образом, полная вероятность вынесения справедливого решения жюри из трех человек равна
p2 + p · (1–p) = p,
что совпадает с соответствующей вероятностью для жюри из одного человека.
Ответ: оба типа жюри имеют одинаковую вероятность вынести правильное решение.
8. Красные и зелёные мячи.
В сумке находятся 6 красных и 8 зелёных мячей. Случайным образом вынимаются 5 из них и помещаются в красную коробку, остальные 9 мячей помещаются в зелёную коробку. Какова вероятность, что количество красных мячей в зелёной коробке плюс количество зелёных мячей в красной коробке не являете простым числом?
Решение:
Обозначим через G количество зелёных мячей в красной коробке. Так как мячей 6 красных и 8 зелёных, то цвета должны быть распределены по коробкам следующим образом:
Красная коробка: G зелёных, (5 – G) красных;
Зелёная коробка: (8 – G) зелёных, (G + 1) красных.
Поэтому число красных мячей в зелёной коробке плюс количество зелёных мячей в красной коробке равно (G + 1) + G = 2G + 1, – нечётному числу. Число G не превосходит 5 – общего количества мячей в красной коробке. Поэтому сумма 2G + 1 может принимать значения от 1 (G = 0) до 11 (G = 5).
Единственное нечётное составное число в этих пределах есть 9. Однако мы должны также включить и число 1, которое не является ни простым, ни составным. Итак, 2G + 1 должно быть равно 0 или 9, что возможно при G = 0 или G = 4.
Вероятность получить выборку с G = 0 (количество способов иметь 5 красных отнесённое к общему числу выборок) равна С65/С145.
Вероятность получить выборку с G = 4 (количество способов иметь 4 зелёных и 1 красный отнесённое к общему числу выборок) равна С84 С61/С145.
Вероятность искомого события найдём как сумму указанных вероятностей:
( С65 + С84 С61) / С145 = (6 + 420) / 2002 = 213 / 1001.
Ответ: 213/1001.
9. В театре.
Восемь юношей и семь девушек независимо приобрели по одному билету в одном и том же театральном ряду, насчитывающем 15 мест. Какое среднее число смежных мест занимают в этом ряду пары?
Решение:
Например, если ряд заполнен следующим образом ЮЮДДЮЮДЮДЮДЮЮДД (здесь Ю обозначает юношу, а Д - девушку), то имеется 9 пар ЮД и ДЮ. Нас интересует среднее число таких пар. Если первые два места в ряду заняты лицами разных полов, то у нас уже имеется искомая пара. Вероятность этого события равна
(8/15) · (7/14) + (7/15) · (8/14) = 8/15.
Более того, 8/15 есть и среднее число пар на первых двух местах, так как
(8/15) · 1 + (7/15) · 0 = 8/15.
Такое же рассуждение применимо к каждой паре смежных мест.
Для определения среднего числа пар молодых людей эту величину надо умножить на число смежных мест, равное 14, что дает 112/15.
Более общим образом, если есть b объектов одного рода и m другого, располагаемых случайным образом в ряд, то среднее число пар, составленных из различных объектов, равно
В нашем примере b = 8, m = 7, и ответ равен 112/15.
Здесь мы существенным образом использовали тот факт, что математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых. Мы нашли среднее число пар ЮД или ДЮ для каждых двух смежных мест и просуммировали по всем таким двойкам.
Ответ: 112/15.
object(ArrayObject)#851 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(131) "Образовательная программа по математике основного общего образования "
["seo_title"] => string(80) "obrazovatiel-naia-proghramma-po-matiematikie-osnovnogho-obshchiegho-obrazovaniia"
["file_id"] => string(6) "119328"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1413386578"
}
}
object(ArrayObject)#873 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(151) "Индивидуально-групповые консультации по математике в 8 классе по подготовке к ГИА "
["seo_title"] => string(89) "individual-no-ghruppovyie-konsul-tatsii-po-matiematikie-v-8-klassie-po-podghotovkie-k-gia"
["file_id"] => string(6) "195544"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1427913510"
}
}
object(ArrayObject)#851 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(160) "Организация индивидуальных и групповых консультаций по подготовке к ГИА по математике"
["seo_title"] => string(96) "orghanizatsiia-individual-nykh-i-ghruppovykh-konsul-tatsii-po-podghotovkie-k-gia-po-matiematikie"
["file_id"] => string(6) "259433"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(7) "prochee"
["date"] => string(10) "1448744069"
}
}
object(ArrayObject)#873 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(109) "Рабочая программа по учебному курсу "Геометрия" для 9 класса"
["seo_title"] => string(63) "rabochaia_programma_po_uchebnomu_kursu_geometriia_dlia_9_klassa"
["file_id"] => string(6) "520708"
["category_seo"] => string(9) "geometria"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1569271088"
}
}
object(ArrayObject)#851 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(69) "Рабочая программа по алгебре (9 класс) "
["seo_title"] => string(44) "rabochaia-proghramma-po-alghiebrie-9-klass-3"
["file_id"] => string(6) "238743"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1444646787"
}
}
Пожалуйста, введите ваш Email.
Если вы хотите увидеть все свои работы, то вам необходимо войти или зарегистрироваться
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
















