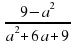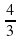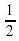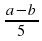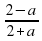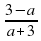Алгебра 7 класс (2 полугодие)
1 вариант
Часть А. Выберите один правильный ответ или напишите свой ответ.
Решение записывать не надо.
А1. Раскройте скобки и приведите подобные слагаемые:-2(а-3b)-6(b+2а)
а) -14а б) 10а в) 12b-14а г) -12b+14а
А2. Если ширина прямоугольника х, а длина в 2 раза больше, то его периметр
равен: а) 3х б) х в) 2
в) 2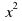 г) 6х
г) 6х
А3. Найдите произведение многочлена и одночлена аb(-2а-3b)
а) -2а2b+3аb2 б)2а2b+3аb2 в)-2а2b-3аb2 г) -2аb-3ab2
А4. Выполните умножение многочленов: (а+4)(а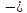 3)
3)
а) а2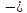 а
а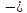 12 б) а2+а
12 б) а2+а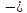 12 в) а2+1 г) а2
12 в) а2+1 г) а2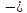 12
12
А5. К многочленам подберите соответствующий им способ разложения на
множители:1) 25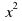 +16
+16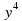 2) 8ху2+4х2 3) а3- b3 4) 3а2+3аb-а-b
2) 8ху2+4х2 3) а3- b3 4) 3а2+3аb-а-b
a) вынесение общего множителя за скобки
б) формула сокращенного умножения
в) не раскладывается на множители г) способ группировки
А6. Укажите выражение, которое не является тождеством:
а) х+5у=5у+х в) х2+25= (х+5)2
б)3bк-3b=3b(к-1) г) к2-n2=(к-n)(n+k)
А7. Выполните деление (25а2-5а):5а а) 5а+1 б) 5а-1 в) 5а г) 5а2-1
А8. Вместо символов * и ** поставьте такие одночлены, чтобы получилось
верное равенство: 81р2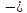 *+q2=(9р
*+q2=(9р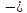 **)2.
**)2.
а) 9pq и q б) 18pq и q2 в) 18pq и q г) 8pq и q2
А9.Укажите выражение, тождественно равное многочлену 4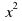 -6ху
-6ху
a) -2х(3у-2х) б) -2х(-3у-2х) в) -2х(3у+2х) г) -2х(2х-3у)
А10. Разложить на множители: к(2+р)+р+2
а) (2+р)(к+1) б) (2+р)(к-1) в) (2+р)к г) (2+р)(к-1)
А11. Известно, что х+у=7, ху=6. Найдите значение выражения х2у+ху2.
А12. Преобразуйте в многочлен выражение 3а(а+2)-(а+3)2
А13. Дана функцияу=f(x), где f(x)=6х-4. Вычислите f(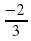 ).
).
Часть В.Записать решение и ответ
В1. Решить уравнение: (4х )2
)2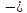 2х(8х
2х(8х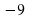 )=1
)=1
В2. Сократить дроби: а)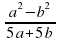 б)
б)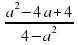
В3. Решить графически уравнение: -х2=х-2
Алгебра 7 класс (2 полугодие)
1 вариант
Часть А. Выберите один правильный ответ или напишите свой ответ.
Решение записывать не надо.
А1. Раскройте скобки и приведите подобные слагаемые: 5(m-2n)+2(5n-m)
а) 3m б) 7m-20n в) 3m+20n г) 7m+20n
А2. Если ширина прямоугольника х, а длина в 2 раза больше, то его площадь
равна: а) 3х б) х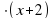 в) 2
в) 2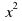 г) 6х
г) 6х
А3. Найдите произведение многочлена и одночлена аb(-2а+3b)
а) -2а2b+3аb2 б)2а2b-3аb2 в)-2а2b-3аb2 г) -2аb+3ab
А4. Выполните умножение многочленов: (5-а)(2+а)
а) а2-а+10 б) а2-а-7 в) 3-а2 г) -а2+3а+10
А5. К многочленам подберите соответствующий им способ разложения на
множители:1) 9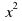 +4
+4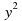 2) а2+аb-2а-2b 3) а4- b4 4) 18х3у2+4х2у
2) а2+аb-2а-2b 3) а4- b4 4) 18х3у2+4х2у
a) вынесение общего множителя за скобки
б) формула сокращенного умножения
в) не раскладывается на множители г) способ группировки
А6. Укажите выражение, которое не является тождеством:
а) 14а-b=b-14а б) (а-2)2= (2-а)2 в) 4аb+4ас=4а(b+с) г) а2-9=(а-3)(а+3)
А7. Выполните деление (7х-21х2):7х а) 1+3х б) -3х в) 1-3х г) 1-3х2
А8. Вместо символов * и ** поставьте такие одночлены, чтобы получилось
верное равенство: 64р2+*+**=(8р+q)2.
а) 8pq и q б) 16pq и q2 в) 16pq и q г) 8pq и q2
А9. Укажите выражение, тождественно равное многочлену 10ab-6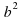
a) -2b(-3b-5a) б) -2b(5a-3b) в) -2b(5a+3b) г) -2b(3b-5a)
А10. Разложить на множители: а(5+b)+b+5
а) (5+b)а б) (5+b)(1-а) в) (5+b)(а-1) г) (5+b)(а+1)
А11. Известно,что х+у= 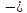 7, ху=3. Найдите значение выражения ху2+ х2у.
7, ху=3. Найдите значение выражения ху2+ х2у.
А12. Преобразуйте в многочлен выражение 4с(с-2)-(с-4)2
А13. Дана функцияу=f(x), где f(x)=-8х+3. Вычислите f(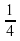 ).
).
Часть В.Записать решение и ответ
В1. Решить уравнение: (6х+5)2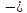 4х(3+9х)=49
4х(3+9х)=49
В2. Сократить дроби: а) 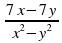 б)
б)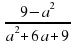
В3.Решить графически уравнение: -х2=х-6
7 класс 2 полугодие
Время выполнения работы и условия ее проведения.
На выполнение работы отводится 1 урок (45 минут).
Дополнительные материалы и оборудование не используются.
Система оценивания.
Критерии выставления оценок:
19 – 17 баллов: «отлично»;
16 – 12 баллов: «хорошо»;
11 – 7 баллов: «удовлетворительно»;
6 – 0 баллов: «неудовлетворительно».
Ключ
| Часть А |
|
| 1 вариант | 2 вариант |
| А1 | а | а |
| А2 | г | в |
| А3 | в | а |
| А4 | б | г |
| А5 | 1в, 2а, 3б, 4г | 1в, 2г, 3б, 4а |
| А6 | в | а |
| А7 | б | в |
| А8 | в | б |
| А9 | а | г |
| А10 | а | г |
| А11 | 42 | -21 |
| А12 | 2а2-9 | 3с2-16 |
| А13 | -8 | 1 |
| Часть В |
| В1 | 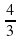
| 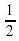
|
| В2 | a) 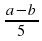 б) б) 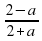 | a)  б) б) 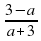 |
| В3 | -2;1 | -3;2 |
За каждый правильный ответ в заданиях части А – 1 балл,
За каждый правильный ответ в заданиях части В – 2 балла
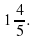
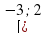
 4.
4.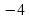 хг) у=4
хг) у=4 и у=0,6х
и у=0,6х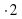 3 +2
3 +2 53.
53.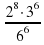 в виде
в виде  ; б)
; б)  ; в)
; в) 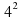 ; г)
; г) 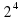
 и у=2х.
и у=2х.
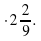
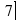 .
.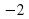 х
х 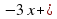 4 в)у=
4 в)у=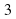 х
х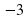
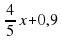 и у=
и у=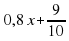
 4+3
4+3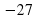 .
.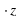 2)
2) 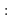
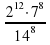 в виде
в виде 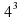 ; г)
; г) 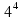
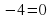 и у=2х.
и у=2х.
 в) 2
в) 2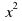 г) 6х
г) 6х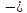 3)
3)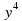 2) 8ху2+4х2 3) а3-
2) 8ху2+4х2 3) а3- 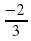 ).
). )2
)2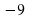 )=1
)=1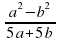 б)
б)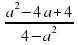
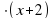 в) 2
в) 2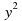 2) а2+а
2) а2+а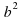
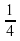 ).
).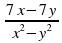 б)
б)