ПОСОБИЕ ПО МАТЕМАТИКЕ
ДЛЯ ОБУЧАЮЩИХСЯ
7- 8 КЛАССОВ
«МОДУЛЬ ЧИСЛА. РЕШЕНИЕ ЗАДАЧ»
АВТОР:
УЧЕНИЦА 7 «А» КЛАССА
МКОУ СОШ № 2 г. АЛАГИРА
БУГУЛОВА АЛЬБИНА
Содержание:
1. Введение……………………………………………………… 2
2. Понятия и определения……………………………………3
2.1 Вспомогательный материал для изучения данной темы……4
3.Решение линейных уравнений, содержащих неизвестное под знаком модуля………….....8
.
4. Графики линейных функций, содержащих выражение под знаком модуля (аналитическое решение)……………..13
4.1. Графики простейших функций, содержащих знак модуля…19
5. Графическое решение линейных уравнений, содержащих модули………………………...21
6.Заключение………………………………………… 27
7. Список использованной литературы……………………………28
Цель работы: считаю, что эта тема требует более глубокого исследования, так как она прослеживается в различных заданиях повышенной сложности, которые предлагают учащимся авторы дидактических материалов, в задачах математических олимпиад, в заданиях вступительных экзаменов в Высшие Учебные Заведения и на ЕГЭ.
Основной целью работы считаю получение расширенной информации о модуле числа, его применении, а также о различных способах решения уравнений, содержащих знак абсолютной величины.
1. Введение.
Понятие «модуль» широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике будут изучаться понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это слово имеет множество значений и применяется не только в математике, физике и технике, но и в архитектуре, программировании и других точных науках.
Считают, что термин предложил использовать Котс, ученик Ньютона. Знак модуля был введен в XIX веке Вейерштрассом.
В архитектуре модуль – исходная единица измерения, устанавливаемая для данного архитектурного сооружения.
В технике – это термин, применяемый в различных областях техники, служащий для обозначения различных коэффициентов и величин, например, модуль упругости, модуль зацепления...
В математике модуль имеет несколько значений, но я буду рассматривать его как абсолютную величину числа.
2. Понятия и определения.
Чтобы лучше изучить данную тему, необходимо вспомнить простейшие определения:
а) уравнение – это равенство, содержащее переменные.
б) уравнение с модулем – это уравнение, содержащее переменную под знаком модуля (абсолютной величины). Например: | x | = 5.
в) решить уравнение – это, значит, найти все его корни, или доказать, что их нет.
г) линейное уравнение с одной переменной – уравнение вида: ax = b, где x – независимая переменная, a и b – некоторые числа.
д) линейная функция – функция вида: y = kx + b, где x – независимая переменная, k и b – некоторые числа.
е) графиком линейной функции является прямая линия.
ж) область определения линейной функции состоит из всех чисел;
если D(у) состоит не из всех чисел, то её график представляет собой соответствующую часть прямой. Например, это может быть полупрямая или отрезок.
з) раскрытие скобок:
1) если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках.
2) чтобы раскрыть скобки, перед которыми стоит знак «-», надо заменить этот знак на «+», поменяв знаки всех слагаемых на противоположные, а потом раскрыть скобки.
2.1. Вспомогательный материал для изучения данной темы.
Для изучения данной темы необходимо познакомиться с графическим решением линейных уравнений и числовыми промежутками.
а) графическое решение уравнений.
Это один из способов решения уравнений.
Его применяют не так часто, так как он занимает в некоторых случаях много времени; результаты, полученные при построении графиков, не всегда являются точными. Суть этого способа заключается в том, чтобы построить графики данных функций.
В случае, если графики пересекутся, то абсциссы точек пересечений данных графиков будут являться корнями данного уравнения.
В случае, если графики не пересекутся, то уравнение корней не имеет.
Абсцисса точки пересечения графиков линейных функций будет корнем линейного уравнения.
Например:
1) х3 = 8.
Решение:
Построим в одной системе координат графики двух функций:
у = х3 и у = 8
D(у): х – любое число D(у): х – любое число
| x | -2 | -1 | 0 | 1 | 2 |
| y | -8 | -1 | 0 | 1 | 8 |

 х = 2.
х = 2.
Ответ: 2.
2) х 2 = -2
Построим в одной системе координат графики двух функций:
у = х 2 у = - 2
D(у): х – любое число D(у): х – любое число х
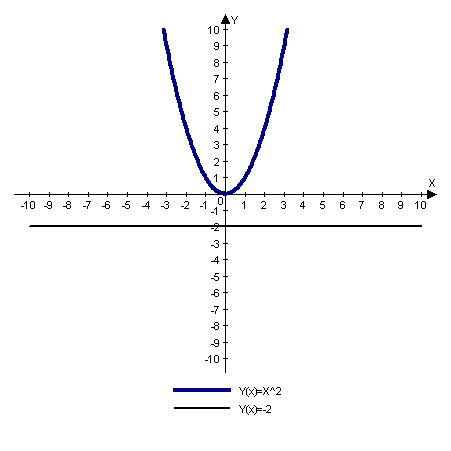
Графики не пересекаются, решений нет.
Ответ: Нет решений.
Числовые промежутки.
1) Отметим на координатной прямой точки с координатами -3 и 2. Если точка расположена между ними, то ей соответствует число, которое больше -3 и меньше 2.



![]()
![]() -3 Х 2
-3 Х 2
Множество всех чисел, удовлетворяющих условию -3
2)Число х, удовлетворяющее условию -3 x 2 изображается точкой, которая лежит между -3 и 2, либо совпадает с одной из них. Обозначение:
[-3; 2].

 / / / / / / / / / / /
/ / / / / / / / / / /

-3 2
3) -3 х 2


 / / / / / / / / / /
/ / / / / / / / / /
-3 2 (-3; 2]
4) -3 x


 / / / / / / / / / /
/ / / / / / / / / /
-3 2 [-3; 2)
5) x 6 
 / / / / / / / / / / / / / / / / / / /
/ / / / / / / / / / / / / / / / / / /
 6 x (6; + ∞)
6 x (6; + ∞)
6) х 6

 / / / / / / / / / / /
/ / / / / / / / / / /
х 6 (∞ ; 6]
7) Запись промежутков:

 ( -∞ ; -2); [-2; 3); [3; + ∞).
( -∞ ; -2); [-2; 3); [3; + ∞).
3. Решение линейных уравнений, содержащих неизвестное под знаком модуля.
(аналитическое решение).
Определение модуля.
Любое число можно изобразить точкой на числовой прямой.
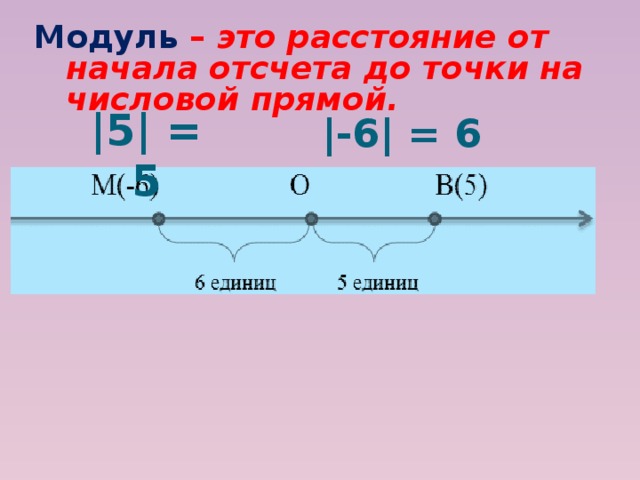
Модулем числа а называют расстояние ( в единичных отрезках) от начала координат до точки А(а).
Пример. Модуль числа 5 равен 5, так как точка В(5) удалена от начала отсчета на 5 единичных отрезков.
|5| = 5.
Модуль числа а или абсолютная величина числа а равна а, если а больше или равно нулю и равна –а, если а меньше нуля.

 а, если а 0
а, если а 0
|а| =
-а, если а
Из определения следует, что для любого числа «а» выполняется неравенство:
|a| 0.
При решении уравнений, содержащих выражения со знаком модуля, удобнее пользоваться алгебраическим определением модуля: модулем положительно- го числа и нуля является само число, модулем отрицательного числа называется противоположное ему положительное число.
Чтобы решить уравнение, содержащее переменную под знаком модуля, надо освободиться от знака модуля, используя его определение.
На практике это делается так:
1) находят подмодульные нули, то есть значения переменной, при которых выражения, стоящие под знаком модуля, обращаются в нуль;
2) разбивают область допустимых значений переменной на промежутки, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак;
3) на каждом из найденных промежутков решают уравнение без знака модуля.
4) Совокупность (объединение) решений указанных промежутков и составляют все решения рассматриваемого уравнения.
Задание 1.
|х – 6| = 9
Решение:
Найдем подмодульный нуль или корень выражения, содержащего знак модуля.
х – 6 = 0,
х = 6.
2)Найденное значение х разбивает числовую прямую на 2 промежутка: х
х 6.
Решение данного уравнения рассматриваем в каждом промежутке отдельно.

3) а) х
- ( х – 6) = 9
- х + 6 = 9
- х = 3
х = - 3, - 3 принадлежит ( - ∞ ; 6 ), значит
- 3 – решение.
б) х 6, получим под модулем положительное число, тогда, раскрываю модуль, имеем:
х – 6 = 9,
х = 15, 15 принадлежит [6;+ ∞ ), значит, 15 – решение.
4) совокупность (объединение) решений указанных промежутков и составляют все решения рассмотренного уравнения.
х = -3 и х = 15.
Ответ: - 3; 15.
Задание 2.
|2х + 3| = 3х –3.
![]() Решение:
Решение:
1) 2)
![]() 2х + 3 = 0,
2х + 3 = 0, 
2х = –3, а) х
х = – 1,5 – (2х + 3) = 3х – 3,
– 2х – 3 = 3х – 3,
– 2х – 3х = – 3 + 3,
–5х = 0,
х = 0, 0 не принадлежит (–∞; -1,5),
значит, 0 не является решением.
б) х – 1,5
2х + 3 = 3х – 3,
2х – 3х = – 3 – 3,
– х = – 6,
х = 6, 6 принадлежит [– 1,5; + ∞),
значит 6 – решение.
Ответ: 6.
Задание 3.
|х + 5| – |х – 3| = 8.
Решение:
1) х + 5 = 0, х – 3 = 0,
х = – 5. х = 3.

3) а) х
– (х + 5) – (– х + 3) = 8,
– х – 5 + х – 3 = 8,
– 8 = 8, неверно, значит, решений нет на промежутке (–∞; – 5)
б) – 5 х
х + 5 – (– х + 3) = 8,
х + 5 + х – 3 = 8,
2х + 2 = 8 ,
2х = 6,
х = 3, 3 не принадлежит [– 5; 3), значит 3 не является корнем уравнения.
в) х 3
х + 5 – (х – 3) = 8,
х + 5 – х + 3 = 8,
8 = 8, верно, значит, любое значение х является корнем уравнения на этом промежутке.
Ответ: [3;+ ∞).
Задание 4.
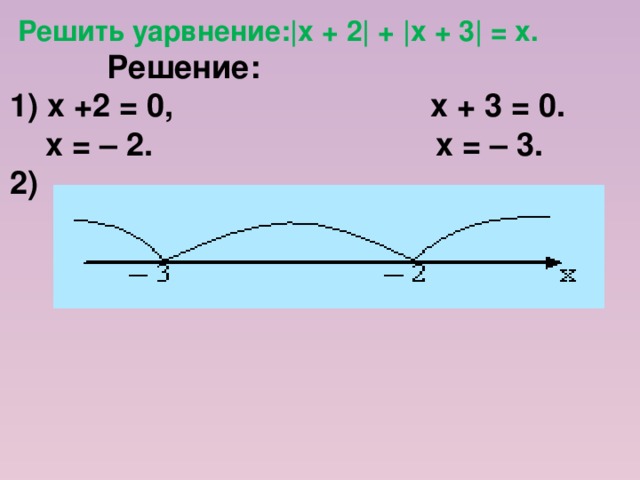
|х + 2| + |х + 3| = х.
Решение:
1) х +2 = 0, х + 3 = 0.
х = – 2. х = – 3.
2)

3) а) х
– (х + 2) – (х + 3) = х,
– х – 2 – х – 3 = х,
– 2х – 5 = х,
– 2х – х = 5,
– 3х = 5,
х = – 1 2 / 3, не принадлежит (–∞; – 3), значит – 1 2 / 3 не является решением.
б) – 3 ≤ х
– (х + 2 ) + х +3 = х,
– х – 2 + х + 3 = х,
– х = – 1,
х = 1, 1 не принадлежит [– 3; – 2), значит, 1 не является решением.
в) х – 2
х + 2 + х + 3 = х,
2х + 5 = х,
2х – х = – 5,
х = – 5, – 5 не принадлежит [– 2;+ ∞), значит, – 5 не является решением.
Ответ: нет решений
Задание 5.
|2 + |2 + х|| = 3.
Решение:
1) 2 + х = 0
 х = – 2.
х = – 2.

2)

 – 2 х
– 2 х
3) а) х
|2 – (2 + х)| = 3,
| 2 – 2 – х | = 3,
| –х | = 3, | х | = 3.
Так как, х
– х = 3,
х = – 3, – 3 принадлежит (–∞; – 2)
б) х – 2
| 2 + (2 + х) |= 3,
| 2 + 2 + х | = 3,
| 4 + х | = 3,
х = – 4 – подмодульный нуль.
х – 4,
– (4 + х) = 3, 4 + х = 3,
– 4 – х = 3, х = – 1 ; – 1 принадлежит [– 4; + ∞)
– х = 7,
х = – 7, – 7 принадлежит (– ∞; – 4)
Учитывая условие: х ≥ – 2, получим, – 1 принадлежит [– 2; + ∞), а – 7 не принадлежит [– 2; + ∞).
Ответ: – 3; – 1.
4. Графики линейных функций, содержащих выражение под знаком модуля.
Для построения графиков функций, содержащих выражение под знаком модуля, сначала находят корни выражений, стоящих под знаком модуля. Эти корни разбивают числовую прямую на промежутки. График строят в каждом промежутке отдельно.
В простейшем случает, когда только одно выражение стоит под знаком модуля и нет слагаемых без знака модуля, можно построить график функций,
опустив знак модуля, а затем часть графика, расположенного в области отрицательных значений y, отобразить симметрично оси ОХ.
Это вытекает из определения модуля числа.
Задание 1.
у = | х | х, если х 0
= | х | х, если х 0
Построение: у=
– х, если х

Заметим, что при построении графика функции у = | х | часть графика у = х, лежащая ниже оси абсцисс, зеркально отражается относительно этой оси.
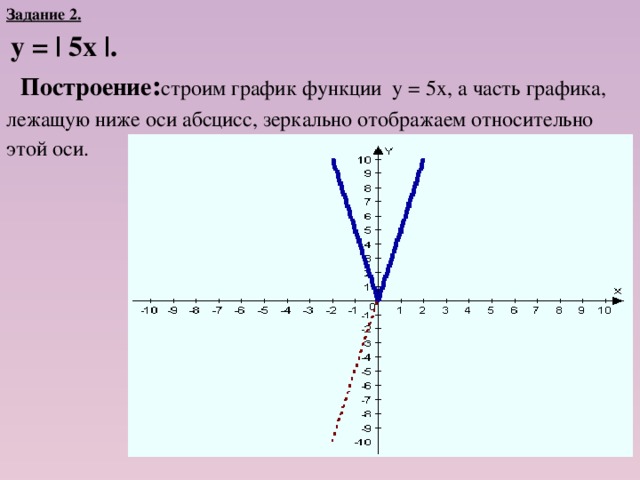
Задание 2.
у = | 5х |.
Построение:
cтроим график функции у = 5х, а часть графика, лежащую ниже оси абсцисс, зеркально отображаем относительно этой оси.

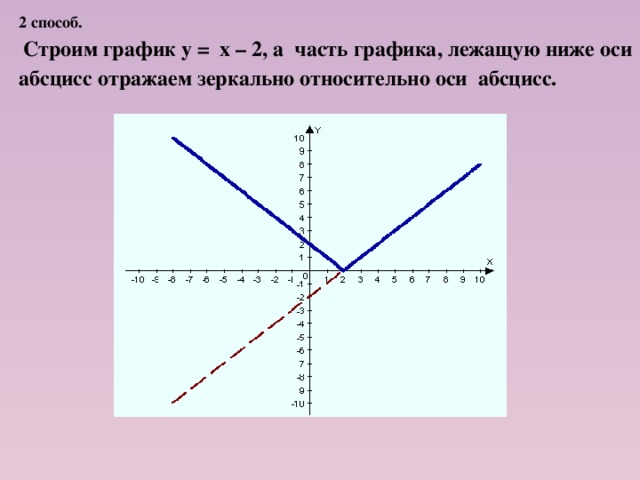
Задание 3.
у = | х – 2 |
Построение:
1 способ.
1) х = 2 – подмодульный нуль.
2)
 – х + 2, х
– х + 2, х
y =
х – 2, х 2
3) Построим графики линейных функций в своих промежутках:
у = – х + 2 у = х – 2




х 0 1 х 0 1

 у 2 1 у – 2 – 1
у 2 1 у – 2 – 1

2 способ.
Строим график у = х – 2, а часть графика, лежащую ниже оси абсцисс отражаем зеркально относительно оси абсцисс.

Задание 4.
у = | х | – 1
Построение:
1) х = 0 – подмодульный нуль.
2) на промежутке х
у = – х – 1



 х 0 1
х 0 1
у – 1 – 2
3) на промежутке х 0 функция примет вид:
у = х – 1

 х 0 1
х 0 1
 у – 1 0
у – 1 0
Задание 5.
у = | х | + х
Построение.
1) подмодульный нуль: х = 0.
2) если х , то у = – х + х = 0; у = 0.
3) если х 0, то у = х + х = 2х; у = 2х.

 х 1
х 1
y 2
Задание 6.
у = | х – 3 | + | 1 – х | – 4
Построение:
1) подмодульные нули: х = 3; х = 1.

2) х у = – 2х.

 х 1
х 1
у – 2
3) 1 ≤ х у = – 2.
4) х 3, тогда у = х – 3 – (1 – х) – 4 = х – 3 – 1 + х – 4 = 2х – 8, у = 2х – 8.


x 4 0
 y 0 2
y 0 2
4
 .1. Графики простейших функций, содержащих знак модуля.
.1. Графики простейших функций, содержащих знак модуля.
Под простейшими функциями понимают алгебраическую сумму модулей линейных выражений.
Сформулируем утверждение, позволяющее, строить графики таких функций, не раскрывая модули (что особенно важно, когда модулей достаточно много);
алгебраическая сумма модулей n-линейных выражений представляет собой кусочно-линейную функцию, график которой состоит из n+1 прямолинейного отрезка. Тогда график может быть построен по n+2 точкам, n из которых представляют собой корни внутримодульных выражений, еще одна -
произвольная точка с абсциссой, меньшей меньшего из этих корней, и последняя – с абсциссой, большей большего из корней.
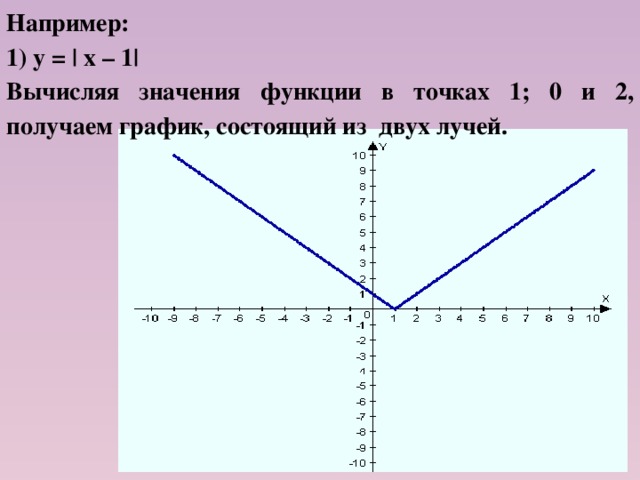
Например:
1) у = | х – 1|
Вычисляя значения функции в точках 1; 0 и 2, получаем график, состоящий из двух лучей.
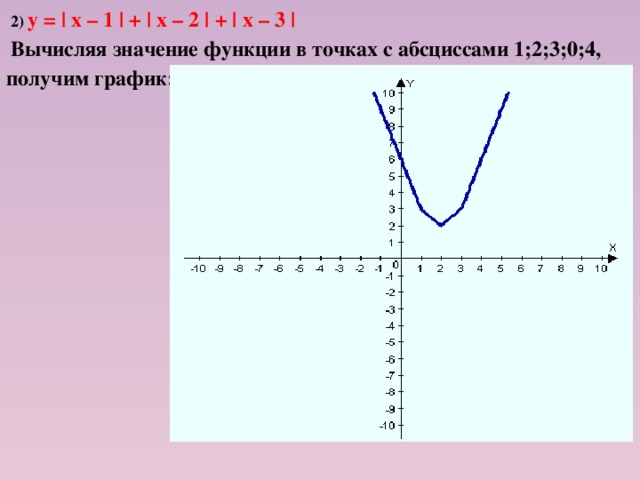
2) у = |х – 1| + |х – 2|
Вычисляя значение функции в точках с абсциссами 1;2;0;3, получаем график:
3) у = | х – 1 | + | х – 2 | + | х – 3 |
Вычисляя значение функции в точках с абсциссами 1;2;3;0;4, получим график:
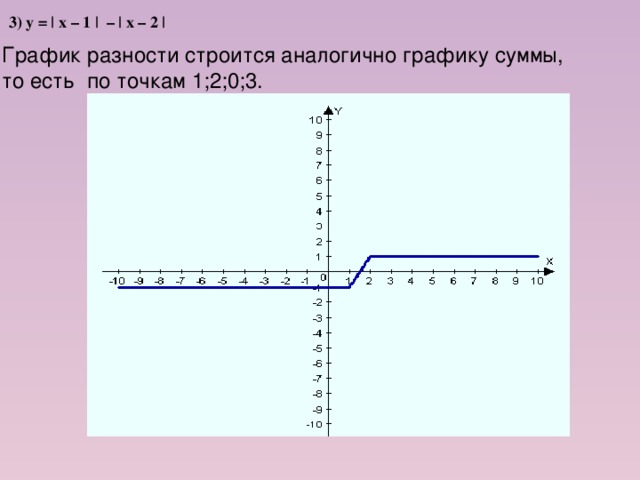
4) у = | х – 1 | – | х – 2 |
График разности строится аналогично графику суммы, то есть по точкам 1;2;0;3.
5. Графическое решение линейных уравнений, содержащих модули.
Задание 1.
Решите уравнение:
| х – 3 | + | 1 – х | = 4.
Решение:
Построим в одной системе координат графики двух функций:
у = | х – 3 | + | 1 – х | и у = 4
1) у = | х – 3 | + |1 – х |
а) подмодульные нули: х = 3, х = 1.
б)



в) х , у = – ( х – 3) + ( 1 – х) = – х + 3 + 1 + х = – 2х + 4


 у = – 2х + 4, х 0 1
у = – 2х + 4, х 0 1
у 4 2
1 х
у = 2
х 3, у = (х – 3) – (1 – х) = х – 3 – 1 + х = 2х – 4

 у = 2х – 4
у = 2х – 4
 x 0 1
x 0 1
y -4 -2
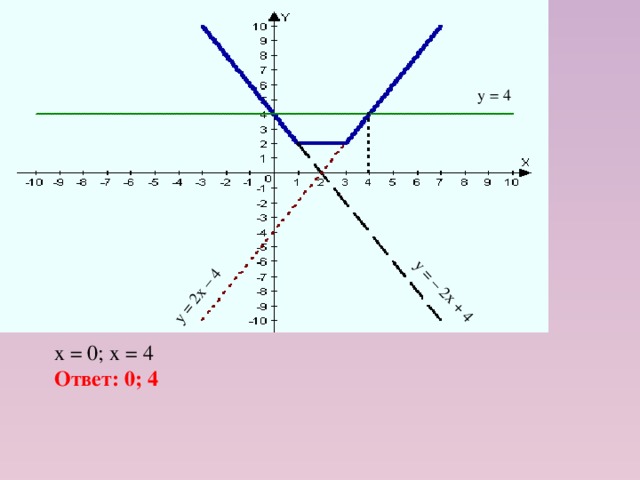
2) у = 4 – прямая линия, параллельная оси абсцисс и проходящая через точку (0;4).
х = 0; х = 4
Ответ: 0; 4
А можно было решить так:
|x - 3| + |1 - x| = 4
|x - 3| + |1 - x| - 4 = 0
Построим в одной системе координат графики:
y = |x - 3| + |1 - x| - 4 и y = 0
Решим это уравнение аналитически.
| х – 3 | + | 1–х | = 4
Решение:
1) подмодульные нули: х = 3; х = 1.
2)
 3) а) х
3) а) х
– (х – 3) + (1 – х) = 4,
–х + 3 + 1– х = 4,
–2х + 4 = 4,
–2х = 0,
х = 0, 0 принадлежит (–∞; 1)
б) 1 х
– (х – 3) – (1 – х) = 4,
– х + 3 – 1 + х = 4,
2 = 4, неверно, решений нет.
в) х 3
(х – 3) – (1 – х) = 4,
х – 3 – 1 + х = 4,
2х – 4 = 4,
2х = 8,
х = 4, 4 принадлежит [3; +∞).
Ответ: 0; 4.
Задание 2.
| х – 5 | + | 5 – х |=0
Решение:
Построим в одной системе координат графики двух функций:
у = /х – 5/ + /5 – х/ и у = 0
1) у = /х – 5/ + /5 – х/
а) подмодульный нуль: х = 5;
б) х , тогда у = – (х – 5) + (5 – х) = – х + 5 + 5 – х = – 2х + 10;

 у = – 2х + 10 х 5 4
у = – 2х + 10 х 5 4
 у 0 2
у 0 2
x≥5, тогда y = (x - 5) – (5 - x) = x – 5 – 5 + x = 2x – 10


у = – 2х - 10 x 5 4
 y 0 - 2
y 0 - 2
2) у = 0, график – ось абсцисс.
Графики пересеклись в точке (5;0), значит корень данного уравнения х = 5.
Ответ: 5.
Решим это уравнение аналитически:
| х – 5 | + | 5 – х | = 0.
Решение:
1)подмодульный нуль: х = 5.
2)

3) х
– х + 5 + 5 – х = 0,
– 2х +10 = 0,
– 2х = – 10,
х = 5, 5 не принадлежит (–∞; 5)
х ≥ 5, тогда (х – 5)-(5 –х)=0,
х –5 –5+х=0,
2х –10=0,
2х=10,
х=5, 5 принадлежит [5; +∞)
Ответ: 5.
Задание 3.
3 – | х –1 | + | х+5 | = 0
Решение:
Построим в одной системе координат графики двух функций:
y = 3 –| х –1 | + | х+5 | и у = 0
1) у = 3 –| х –1 | + | х + 5 |
а) подмодульные нули: х = 1; х = 5
б)

в) х , у = 3 + (х – 1) – (х + 5) = 3 + х – 1 – х – 5 = -3,
у = -3
–5 х


у = 2х + 7 х 0 -5
 у 7 3
у 7 3
х ≥ 1, у = 3 – (х – 1) + (х + 5) = 3 – х + 1 + х + 5 = 9,
у = 9
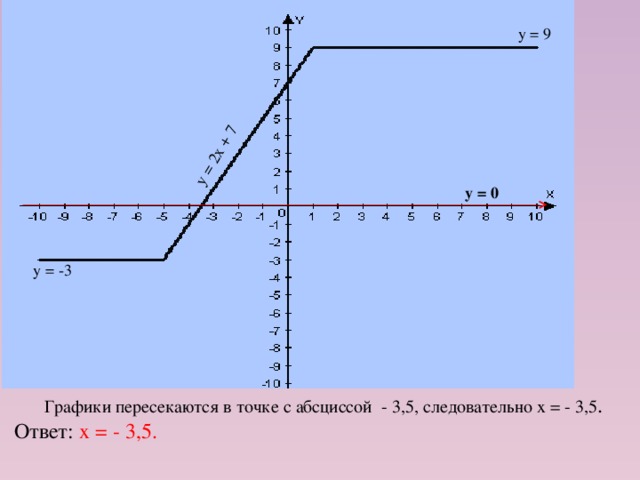
2) у = 0
Графики пересекаются в точке с абсциссой - 3,5, следовательно х = - 3,5.
Ответ: х = - 3,5.
Решим это уравнение аналитически:
3 – | х –1 | + | х + 5 | = 0
Решение:
1) подмодульные нули: х = 1, х = -5.
2)

3) х
3 + х – 1 – х – 5 = 0,
- 3 = 0, неверно, решений нет.
-5 х
3 + х –1 + х + 5 = 0,
2х + 7 = 0,
2х = -7
х = -3,5, -3,5 принадлежит [-5; 1)
х 1, тогда 3 – (х – 1) + (х + 5) = 0,
3 – х + 1 + х + 5 = 0,
9 = 0, неверно, решений нет.
Ответ: x = - 3,5.
Имея корни решенных уравнений и рассматривая графики построенных функций, можно сделать вывод: корни полученных уравнений – это абсциссы точек пересечения графиков с осью ОХ.
6. Заключение.
Дорогие ребята!
Я рассмотрела аналитические и графические способы решения линейных уравнений с модулями, построение графиков линейных функций, содержащих выражение под знаком модуля, графики простейших функций, содержащих знак модуля.
В ходе работы прочитано и изучено немало дополнительной литературы. Полученные знания помогут легко выбирать рациональный способ решения уравнений.
Работать было очень интересно!
УСПЕХОВ ВАМ!!!
30

 х = 2.
х = 2.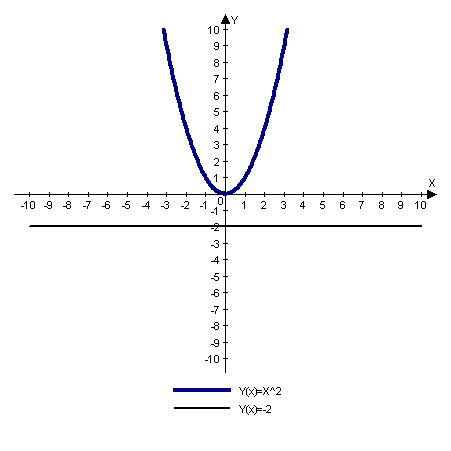










 / / / / / / / / / /
/ / / / / / / / / / 


 ( -∞ ; -2); [-2; 3); [3; + ∞).
( -∞ ; -2); [-2; 3); [3; + ∞).
 а, если а 0
а, если а 0

 х = – 2.
х = – 2.

 – 2 х
– 2 х  = | х | х, если х 0
= | х | х, если х 0




















 6. Решение данного уравнения рассматриваем в каждом промежутке отдельно." width="640"
6. Решение данного уравнения рассматриваем в каждом промежутке отдельно." width="640"

 6, получим под модулем положительное число, тогда, раскрываю модуль, имеем: х – 6 = 9, х = 15, 15 принадлежит [6;+ ∞ ), значит, 15 – решение. 4) совокупность (объединение) решений указанных промежутков и составляют все решения рассмотренного уравнения. х = -3 и х = 15. Ответ: - 3; 15." width="640"
6, получим под модулем положительное число, тогда, раскрываю модуль, имеем: х – 6 = 9, х = 15, 15 принадлежит [6;+ ∞ ), значит, 15 – решение. 4) совокупность (объединение) решений указанных промежутков и составляют все решения рассмотренного уравнения. х = -3 и х = 15. Ответ: - 3; 15." width="640"


 3 х + 5 – (х – 3) = 8, х + 5 – х + 3 = 8, 8 = 8, верно, значит, любое значение х является корнем уравнения на этом промежутке. Ответ: [3;+ ∞)." width="640"
3 х + 5 – (х – 3) = 8, х + 5 – х + 3 = 8, 8 = 8, верно, значит, любое значение х является корнем уравнения на этом промежутке. Ответ: [3;+ ∞)." width="640"

 – 2 х + 2 + х + 3 = х, 2х + 5 = х, 2х – х = – 5, х = – 5, – 5 не принадлежит [– 2;+ ∞), значит, – 5 не является решением. Ответ: нет решений " width="640"
– 2 х + 2 + х + 3 = х, 2х + 5 = х, 2х – х = – 5, х = – 5, – 5 не принадлежит [– 2;+ ∞), значит, – 5 не является решением. Ответ: нет решений " width="640"

 0 у= – х, если х при построении графика функции у = | х | часть графика у = х, лежащая ниже оси абсцисс, зеркально отражается относительно этой оси." width="640"
0 у= – х, если х при построении графика функции у = | х | часть графика у = х, лежащая ниже оси абсцисс, зеркально отражается относительно этой оси." width="640"
 2 3) Построим графики линейных функций в своих промежутках: у = – х + 2 у = х – 2 х 0 1 х 0 1 у – 2 – 1 у 2 1" width="640"
2 3) Построим графики линейных функций в своих промежутках: у = – х + 2 у = х – 2 х 0 1 х 0 1 у – 2 – 1 у 2 1" width="640"

 0, то у = х + х = 2х; у = 2х . Задание 4. " width="640"
0, то у = х + х = 2х; у = 2х . Задание 4. " width="640"
 3, тогда у = х – 3 – (1 – х) – 4 = х – 3 – 1 + х – 4 = 2х – 8, у = 2х – 8 . Задание 5. у = | х – 3 | + | 1 – х | – 4 Построение: 1) подмодульные нули: х = 3; х = 1." width="640"
3, тогда у = х – 3 – (1 – х) – 4 = х – 3 – 1 + х – 4 = 2х – 8, у = 2х – 8 . Задание 5. у = | х – 3 | + | 1 – х | – 4 Построение: 1) подмодульные нули: х = 3; х = 1." width="640"



 3, у = (х – 3) – (1 – х) = х – 3 – 1 + х = 2х у = 2х – 4 2) у = 4 – прямая линия, параллельная оси абсцисс и проходящая через точку (0;4)." width="640"
3, у = (х – 3) – (1 – х) = х – 3 – 1 + х = 2х у = 2х – 4 2) у = 4 – прямая линия, параллельная оси абсцисс и проходящая через точку (0;4)." width="640"
 3 (х – 3) – (1 – х) = 4, х – 3 – 1 + х = 4, 2х – 4 = 4, 2х = 8, х = 4, 4 принадлежит [3; +∞). Ответ: 0; 4." width="640"
3 (х – 3) – (1 – х) = 4, х – 3 – 1 + х = 4, 2х – 4 = 4, 2х = 8, х = 4, 4 принадлежит [3; +∞). Ответ: 0; 4." width="640"

 1, тогда 3 – (х – 1) + (х + 5) = 0, 3 – х + 1 + х + 5 = 0, 9 = 0, неверно, решений нет. От вет: x = - 3,5." width="640"
1, тогда 3 – (х – 1) + (х + 5) = 0, 3 – х + 1 + х + 5 = 0, 9 = 0, неверно, решений нет. От вет: x = - 3,5." width="640"




















