Исследовательская работа "Геометрические головоломки"

Оглавление

1.Введение………………………………………………………………… 2 -3 стр.

2.Основная часть …...……..….................................................................. 4 – 10стр.

2.1. Виды геометрических головоломок…………………………4 стр.

2.2. История зарождения геометрических головоломок………. 4 - 6 стр.

2.3. Правила геометрических головоломок и изготовление…... 6 - 9 стр.

2.4. Применение геометрических головоломок в современном мире...................................................................................................... 9 стр.

3. Результаты анкетирования и эксперимента……................................ 10 -12 стр.

4. Выводы..................................................................................................... 13 стр.

5. Список использованной литературы и источников…........................ 14 стр.

6. Приложение …………………………………………………………. 15-17стр.

1. Введение

На уроках математики мы познакомились с геометрическими фигурами научились чертить их на линованной и нелинованной бумаге, вырезать из картона и составлять из них новые фигуры в виде предметов быта, животных, растений. Это оказалось очень увлекательным занятием. Учитель математики сказала, что фигуры используются ещё и в геометрических головоломках: «Танграм», «Колумбово яйцо», «Полимино».Стало интересно узнать, что такое головоломка, где они появились и встречаются ли сейчас.

Не все учебники математики содержат задания направленные на решение геометрических головоломок. Внеурочная деятельность учащихся начального и среднего звеньев школытакже не предусматривает рассмотрение указанных задач. На практике можно убедиться, что молодое поколение даже не слышали о многих геометрических головоломках, хотя и понимают значимость их на развитие умственных способностей людей. Самое главное, что в олимпиадах и конкурсах по математике в последнее время включают задания с геометрическими головоломками. Всё это определяетактуальность данной исследовательской работы.

Несомненной является и новизнаданной работы, так какисследования по теме «Геометрические головоломки» в МКОУ «Брылинская СОШ» ранее не проводились и их изучение не предусмотрено школьной программой по математике.

Данное исследование может быть использовано учителем математики на уроках в виде дополнительных заданий для развития воображения, мышления, интереса к предмету. Также возможно применение нашего материала во внеурочной деятельности, например, учителями начальной школы или воспитателями в детском саду. Хотелось бы, чтобы геометрические головоломки стали альтернативой телефонным играм в организации досуга школьников (например, на переменах между уроками). Это говорит о высоком практическом значении исследования.

В ходе исследования использованы материалы следующих сайтов: «Мир детских эмоций и чувств» (https://ncuxolog.ru/zagadochnyj-tangram), «Детский сайт для родителей. Развитие детей» (http://razvitiedetei.info/dosug/geometricheskij-konstruktor-tangram.html), «Волшебная шкатулка. Занимательная математика» (http://novijmir.blogspot.ru/p/blog-page_17.html). С этих сайтов мы взяли материал о истории зарождения геометрических головоломок, правила игр и способы изготовления элементов геометрических головоломок.Проанализировали статью, представленную на web - страницах сайта«Ярмарка мастеров» (https://www.livemaster.ru/topic/463495-v-mire-tangram-igrushka-na-vse-vremena), в которой описывается применение геометрических головоломок в жизни людей. Прочитали работу Д.Головина, Е. Дубровского и др. в электронном журнале «Юный ученый». В словарях русского языка С.И. Ожигова и Т.В. Ефремова рассмотрели толкование некоторых слов по нашей теме.

Объект исследования:игры«Танграм», «Колумбово яйцо», «Полимино».

Предмет: знание геометрических головоломок и интерес людей к ним.

Цель исследования: выявление степени знания и увлеченности людьми геометрическими головоломками.

Задачи:

• Определить виды головоломок.

• Изучить историю появления геометрических головоломок.

• Изучить правила игры.

• Выявить применение геометрических головоломок в современном мире.

• Провести опрос среди населения на знание и увлеченность геометрическими головоломками.

• Провести эксперимент среди школьников.

• Систематизировать полученные данные в диаграммах.

Гипотеза - предположим,чтоучащиеся и взрослые люди мало знают о геометрических головоломках и мало ими увлекаются.

Методы исследования:

• теоретический (изучение фактов из литературы,Интернет-источников);

• эмпирический (эксперимент, анкетирование населения);

• математический (представление информации в диаграммах).

Этапы работы:

• определение темы;

• определение цели и задач;

• выдвижение гипотезы;

• отбор информации из различных источников;

• проведение анкетирования населения;

• систематизация полученной информации ;

• оформление работы;

• презентация работы.

Сроки работы над исследованием: декабрь 2016 -март 2017 г.

1. Основная часть

   1. Виды головоломок

По новому словарю русского языка Т.В. Ефремова - головоломка:

а) Специально подобранная загадка, задача и т.п., для решения которой требуются сообразительность и знания в соответствующей области.

б) Забавная поделка, состоящая из различных соединенных между собою элементов, которые необходимо разъединить.

2) перен. Какие-л. сложные проблемы, решение которых требует большого труда[2].

Виды головоломок:

1. Устные головоломки – это головоломки, условия которых может быть передано в устной речи без привлечения каких – либо дополнительных предметов. К ним можно отнести: загадки, шарады, парадоксы, игру данетки.

2. Головоломки с предметами – это головоломки, в которых активно используются обычные бытовые предметы: головоломки со спичками, монетами, карточные головоломки.

3. Механические головоломки – это класс головоломок, которые специально были изготовлены как головоломки. Это всевозможные проволочные головоломки, головоломки типа Кубика Рубика, пазлы, пентамино и др.

4. Печатные головоломки – это те головоломки, для которых необходима бумага и карандаш. Они могут быть напечатаны или нарисованы. К таким головоломкам относятся сконворды, кроссворды, ребусы и т.д.

5. Компьютерные головоломки.[5.7]

Среди множества головоломок имеет особое значение геометрические, т. е. такие, в которых применяются геометрические фигуры: «Танграм», «Колумбово яйцо», «Полимино».

1. История зарождения геометрических головоломок

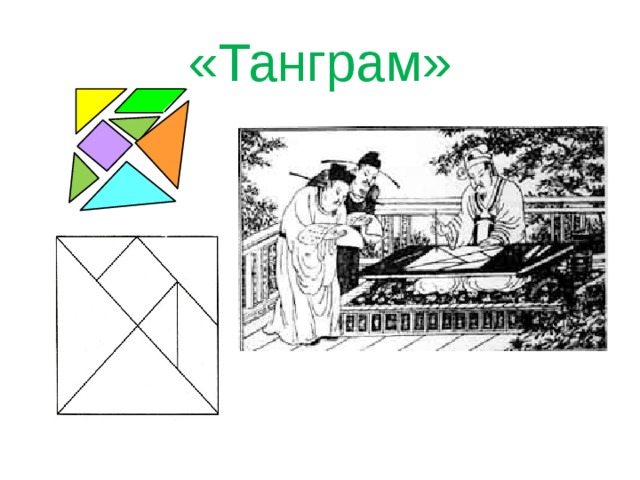
«Танграм»

Игра родилась в Китае более 4000 лет назад. Хотя слово «Танграм» было придумано чуть более века назад в Северной Америке, китайская игра была известна под названием «доска из семи фигур мудрости»[5.2].

В учебнике Г.К. Муравина, О.В. Муравиной «Математика. 5класс.» говорится о том, что название «Танграм» возникло в Европе и, вероятнее всего, переводится как «китайские буквы», так как в переводе с греческого «тань» означает «китаец», а «грамм» - «буква». Рассказывают, что Наполеон, находясь в изгнании на острове Св. Елены, часами занимался составлением картинок из элементов «танграма»[3].

Существует множество легенд о зарождении игры. В нашей работе приводим три, самые занимательные и поучительные.

Легенда первая: версия про разбитую плитку.

Более 4000 тысяч лет назад у одного человека из рук выпала фарфоровая плитка и разбилась на семь частей. Расстроенный, он в спешке старался ее сложить, но каждый раз получал все новые интересные изображения. Это занятие оказалось настолько увлекательным, что впоследствии квадрат, составленный из семи геометрических фигур, назвали Доской Мудрости. 

Легенда вторая: три мудреца придумали «Ши-Чао-Тю».

Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Мальчик рос здоровым и сообразительным не по летам.Одно беспокоило старого императора: его сын, будущий властелин огромной страны, не хотел учиться. Мальчику доставляло большее удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали "Ши-Чао-Тю"- квадрат, разрезанный на семь частей[5.2].

Легенда третья: семь книг Тана.

Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству. Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа «инь и ян». Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудию труда, мебель, одежда и архитектурные сооружения. Лойд часто цитирует высказывания Конфуция, философа по имени Шуфуце, комментатора Ли Хуанчжан и вымышленного профессора Челленора. Ли Хуанчжан упоминается в связи с тем, что по преданию он знал все фигуры из семи книг Тана прежде, чем научился говорить. Встречаются у Лойда и ссылки на «известные» китайские пословицы типа «Только глупец взялся бы написать восьмую книгу Тана»[5.6].

Колумбово яйцо— крылатое выражение, обозначающее неожиданно простой выход из затруднительного положения[5.3] .

Существует красивый миф о происхождении этого выражения.

От­крыватель Америки Колумб был приглашен к всемогущему кардиналу Мендозе. За столом, по просьбе гостей, он начал рассказывать, как именно был им открыт Новый Свет (кото­рый, впрочем, он считал Индией). Кто-то из присутствую­щих, человек ограниченный, но самоуверенный, пожав пле­чами, сказал: «Так просто всё?»
Колумб взглянул на него и протянул ему лежавшее на блюде куриное яйцо: «Сделайте так, чтобы оно стояло на своем носке». Разумеется, попытки установить яйцо успехом не увенчались. «Это немыслимо...» - сказал обескураженный собеседник Колумба. «Это очень просто!» - с усмешкой от­ветил мореплаватель и, разбив о стол носок яйца, без труда заставил его стоять.

Выражение «колумбово яйцо» - стало воплощением ост­роумного и неожиданного выхода из затруднения, синонимом простого разрешения трудных вопросов.[5.4]А затем стало названием геометрической головоломки.Суть задания состоит в том, чтобы из деталей конструктора «Колумбово яйцо» сложить фигурки. Это могут быть люди, животные или птицы, транспорт и мебель, цветы, буквы и цифры.

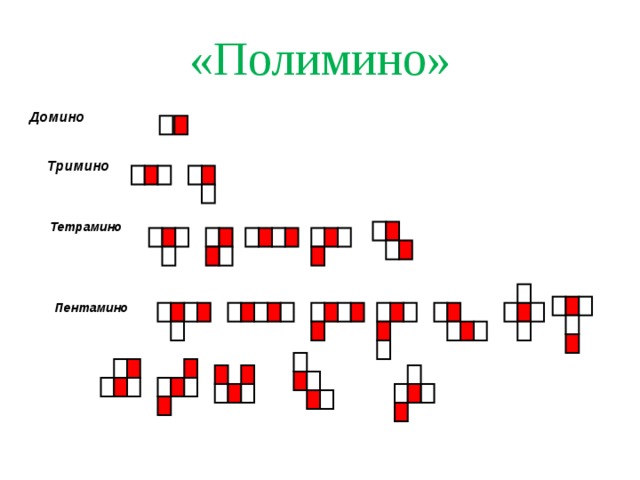
«Полимино»

Полимино, или полиомино (англ. polyomino) — плоские геометрические фигуры, образованные путём соединения нескольких одноклеточных квадратов по их сторонам.

Полимино использовались в занимательной математике, по крайней мере с 1907 года, а известны были ещё в древности. Многие результаты с фигурами, содержащими от 1 до 6 квадратов, были впервые опубликованы в журнале «FairyChessReview» в период с 1937 по 1957 г., под названием «проблемы рассечения». Название «полимино» или «полиомино» было придумано Соломоном Голомбом в 1953 году и затем популяризировано Мартином Гарднером[1].

2.3. Правила головоломок и изготовлениеэлементов для игры

«Танграм»

В игре – головоломке «Танграм» главной целью является создание фигур из 7 элементов –танов, полученных разрезанием  квадрата на семь частей – два больших (1, 2),  два маленьких (3, 4) и один средний треугольник (5), один квадрат (6)  и один параллелограмм (7)[5.6](рис.1). При решении головоломки требуется соблюдать условия: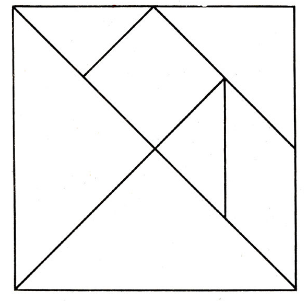

Рисунок 1. Основа игры "Танграм"

- при составлении изображений используются все семь фигур;

- фигуры должны быть в одной плоскости, т.е. не должны перекрывать друг друга, располагаться поверх других частей;

-все части должны быть смежными, т.е. иметь точку соприкосновения с другими частями[5.2].

На курсе «Математика в задачах» учащиеся 6 класса познакомились с «Танграм» и попробовали составить свои фигуры (Приложение №1).

«Колумбово яйцо»

В головоломке «Колумбово яйцо» так же, как и в «Танграм», необходимо создавать фигуры из элементов, которые получают из овала. В игре существует только два правила, которые нельзя нарушать: первое - нужно использовать все детали- 10штук; второе - части не должны пересекаться, их следует прикладывать друг к другу(рис. 2).

 Для изготовления игры берут за основу овал (например 15 на 12 см), разрезают, как на рисунке 2. Получают 10 частей.А можно поступить по - другому — в основе яйцо. В окружности проводим 2 взаимно перпендикулярных диаметра — это первые линии, по которым в дальнейшем разрезаем яйцо. Затем в крайних точках одного отрезка проводим 2 окружности, радиус каждой окружности равен диаметру  первой окружности. Дальше, проводим линии, соединяющие три точки первой окружности, чтобы получить большой треугольник (на рисунке красные линии), заканчиваются линии на границе с большими окружностями.Затем чертим еще 3 окружности с одинаковым радиусом:

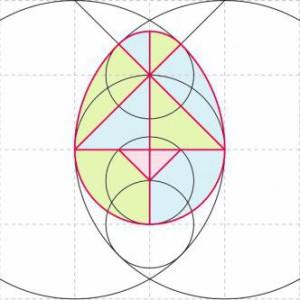
Рисунок 2. Основа игры "Колумбово яйцо"

1 окружность: центр — вершина треугольника, радиус — отрезок от вершины треугольника до линии пересечения с большой окружностью.

2 окружность: центр — точка пересечения диаметра с окружностью (внизу).

3 окружность: центр — точка пересечения 2 окружности с диаметром.

1 окружность установила границы яйца, а 2 и 3 окружности дают точки для построения маленького треугольника. На рисунке линии красного цвета.

Обводим то что нам надо вырезать (на рисунке красный цвет)

1. само яйцо

2. вверху удлиняем линию диаметра до границы яйца

3. линии вверху яйца — линии через точки диаметра до пересечения с большой окружностью

внизу строим маленький треугольник, через точки пересечения окружности 2 и 3 с диаметром первой окружности.Сверяемся с рисунком, получилось 10 частей головоломки. Вырезаем и играем[5.5]. Из них можно составить множество интересных фигур - животных, птиц и т.д., лишь бы был интерес и воображение.

Рисунок 3. Фигуры из элементов "Колумбово яйцо"

«Полимино»

Головоломку «Полимино» можно подразделить на виды, в зависимости от количества квадратиков (рис.3). Из квадратов, соседствующих сторонами, можно сложить n-ое количество различных простых фигур (рис.2), а из них более сложные геометрические фигуры.

Рисунок 4. Виды полимино.

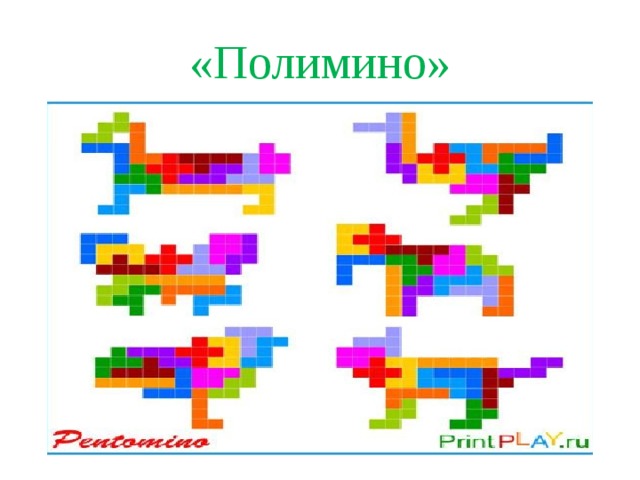
Все названия имеют происхождение от греческого языка: «до» - два, «три» - три, «тетра» - четыре, «пента» - пять. Особый интерес для среднего звена может составить «Пентамино»: составление из 5 квадратиков различных 12 простых фигур (основа игры), а затем - более сложные геометрические фигуры. Например: сложить из всех фигурок, без перекрытий и зазоров, прямоугольник и т.д.

Рисунок 5. Фигуры Пентамино.

2.4. Применение геометрических головоломок в современном мире

Геометрические фигуры и наука о изучении их свойств появились в процессе деятельности человека. Можно предположить, что и элементы геометрических головоломок также участвуют в жизни современного человека.

Танграм во всех его проявлениях можно встретить начиная от дизайна одежды, заканчивая архитектурой и ландшафтным дизайном. Самое удачное применение танграма, пожалуй в качестве мебели. Вся мебель, построенная по принципу танграма, очень удобна и функциональна. Каждый раз она может видоизменятся в зависимости от настроения и желания хозяина. Сами производители выпустили вместе с инструкцией по сборке несколько страниц с идеями для библиотеки, гостиной, спальни и детской.   Самое вкусное применение танграма в шоколаде. [5.6] (Приложение №2).

1. Результаты анкетирования и эксперимента

Были опрошены люди от 9 до 60 лет.

Вопросы анкеты:

1. Фамилия, имя, отчество.

2. Сколько Вам полных лет.

3. Какие геометрические головоломки Вы знаете.

4. Какие качества и способности, по Вашему мнению, развивают у человека занятия геометрическими головоломками.

5. Где в современном мире встречали геометрические головоломки. (Приложение №3)

Опрос показал, что учащиеся мало знают геометрические головоломки.

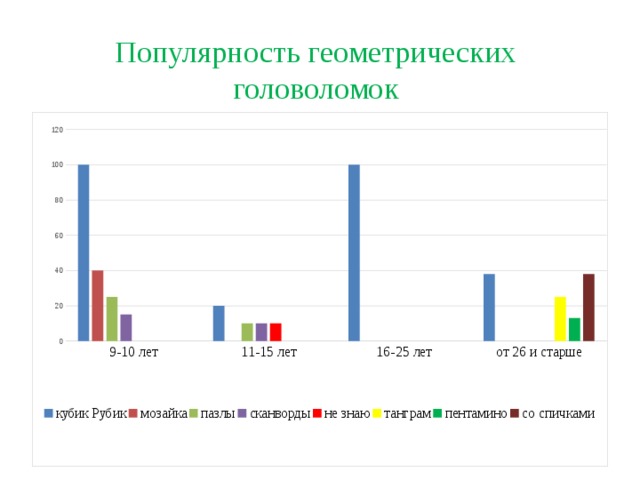
Диаграмма №1.

Анализируя данные, выяснили, что школьники начального и среднего звеньев не знают геометрических головоломок «Танграм», «Колумбово яйцо», «Полимино», только люди старшего поколения в малой степени знакомы с этими играми. Самая популярная головоломка среди населения - кубик Рубик.Дети 9-10 лет увлекаются мозаикой и пазлами, а вот подростки, кроме кубика Рубика ничего не знают.

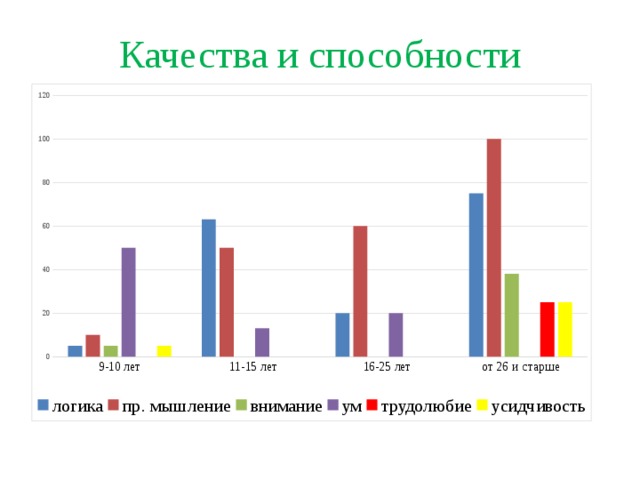
Диаграмма №2

Все, даже младшие школьники, понимают, что геометрические головоломки развивают определенные навыки и качества у людей, т.е. занятия головоломками – не пустая трата времени. Как дети, так и взрослые в основном отмечают развитие логического и пространственного мышления, «ум». Люди от 25 лет и старше обращают внимание на то, что увлечение геометрическими головоломками формирует усидчивость, трудолюбие и внимание.

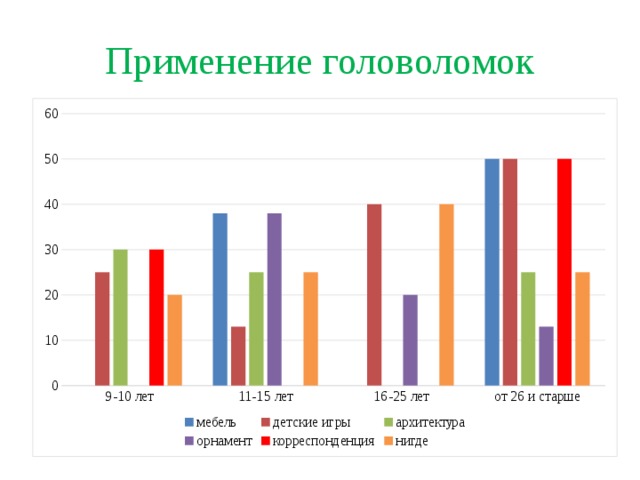
Диаграмма №3

Оказалось, что многие (от 20 – 40% анкетируемых) не видели и не знают, где можно встретить в современном мире применение геометрических головоломок «Танграм», «Колумбово яйцо», «Полимино» и т.д. Остальные отмечают их использование в детских играх, мебели, различных орнаментах, в архитектуре, в журналах и газетах.

В ходе исследования нами проведён эксперимент, в ходе которого на переменах школьникам предложены механические (геометрические) головоломки. Результаты эксперимента показали невысокий уровень заинтересованности школьников в решении геометрических головоломок ( 14 % подростков).

1. Выводы

Проведенное исследование показывает, что взрослые люди мало интересуются и увлекаются геометрическими головоломками, дети же о «Танграм», «Колумбово яйцо» и «Полимино» совсем не знают. Это означает, что в дошкольных учреждениях и в начальной школе не используют задания геометрических головоломок либо не говорят, как называется данная игра. Все участники анкетирования отмечают положительное влияние занятий геометрическими головоломками на развитие умственных способностей у человека.

В ходе работы:

1. Определены виды головоломок.

2. Изучена история появления отдельных типов головоломок.

3. Изучены правила игр.

4. Выявлено применение геометрических головоломок в современном мире.

5. Проведен опрос населения, с целью выявления степени знания и увлеченности геометрическими головоломками;

6. Проведен эксперимент среди школьников;

7. Систематизированы полученные данные в диаграммах и сделаны выводы.

В ходе исследования доказано, что учащиеся и взрослые люди мало знают о геометрических головоломках и мало ими увлекаются.

Перспектива дальнейшего исследования – реализация проекта «Геометрические головоломки в школе», цель которого – внедрение геометрических головоломок во внеурочную деятельность школьников.

1. Список использованной литературы и источников

1. Головин, Д. А., Дубровский Е. Э., Ловков К. И., Шамшурина Ю. С., Ястребов М. И., Шмелева О. В. Математические головоломки: полимино. // Юный ученый. — 2016. — №6.1. — С. 21-23.

2. Ефремов, Т.В. Новый словарь русского языка. Толково – словообразовательный словарь.: Ок.160 000 слов/ Т.В. Ефремов – М.: Дрофа, 2000. – 1233с

3. Муравин, Г.К. Математика. 5 кл..: учеб. для общеобразовательных учреждений/ Г.К. Муравин, О.В. Муравина. – 3-е издю, перераб. – М.: Дрофа, 2007.-315с.: ил.

4. Ожегов,С.И. Словарь русского языка: Ок.53 000 слов/ С.И. Ожегов; Под общ. ред. проф. Л.И. Скворцова – М.: ООО «Издательство Оникс», 2011. – 1200с.

5. Интернет - ресурсы:

1. http://razvitiedetei.info/dosug/geometricheskij-konstruktor-tangram.html- Детский сайт для родителей. Развитие детей.

2. https://ncuxolog.ru/zagadochnyj-tangram- Мир детских эмоций и чувств.

3. https://ru.wikipedia.org/wiki-ВикипедиЯ

4. http://fb.ru/article/173523/kolumbovo-yaytso-uvlekatelnaya-golovolomka-dlya-detey-i-vzroslyih - Fb.ru

5. http://novijmir.blogspot.ru/p/blog-page_17.html-Волшебная шкатулка. Занимательная математика.

6. https://www.livemaster.ru/topic/463495-v-mire-tangram-igrushka-na-vse-vremena- журнал «Ярмарка мастеров»

7. http://fitnessbrain.ru/golovolomki/golovolomka - Прокачай свой мозг. Фитнес – клуб для мозга.

Приложение №1

Фигуры головоломки «Танграм», составленные учащимися 6 класса МКОУ «Брылинская СОШ»

Приложение №2

Примеры применение «Танграма» в современной жизни человека

  

 

 

 

 

Приложение №3

14

Муниципальное казенное общеобразовательное учреждение

«Брылинская средняя общеобразовательная школа»

Каргапольского района Курганской области

Исследовательская работа

Геометрические головоломки

Автор: Афанасьева Юлия Максимовна,

учащаяся 5 класса

Руководитель: Ефимова В.С.,

учитель математики

МКОУ «Брылинская СОШ»,

высшая квалификационная категория

Брылино, 2017

Муниципальное казенное общеобразовательное учреждение

«Брылинская средняя общеобразовательная школа»

Каргапольского района Курганской области

Исследовательская работа Геометрические головоломки

Автор: Афанасьева Юлия Максимовна ,

учащаяся 5 класса

Руководитель: Ефимова В.С.,

учитель математики

МКОУ «Брылинская СОШ»,

высшая квалификационная категория

 

  Брылино, 2017

Цель: выявление степени знания и увлеченности людьми геометрическими головоломками.

Задачи:

• Определить виды головоломок.
• Изучить историю появления геометрических головоломок.
• Изучить правила игры.
• Выявить применение геометрических головоломок в современном мире.
• Провести опрос среди населения на знание и увлеченность геометрическими головоломками.
• Систематизировать полученные данные в диаграммах.

Методы исследования:

• теоретический (изучение фактов из литературы, Интернет-источников );
• эмпирический (проведение анкетирование населения, эксперимент );
• математический (представление информации в диаграммах) .

Виды головоломок

• Устные головоломки.
• Головоломки с предметами.
• Механические головоломки.
• Печатные головоломки.
• Компьютерные головоломки .

«Танграм»

«Фигуры из танграма»

«Колумбово яйцо»

«Колумбово яйцо»

«Полимино»

Мартин Гарднер

Соломон Голомб

«Полимино»

Домино

Тримино

Тетрамино

Пентамино

«Полимино»

Применение геометрических головоломок

Популярность геометрических головоломок

Качества и способности

Применение головоломок

Заключение

Проведенное исследование показывает, что взрослые люди мало интересуются и увлекаются геометрическими головоломками, дети же о «Танграм», «Колумбово яйцо» и «Полимино» совсем не знают. Это означает, что в дошкольных учреждениях и в начальной школе не используют задания геометрических головоломок, либо не говорят, как называется данная игра. Все опрошенные отмечают положительное влияние занятиями геометрическими головоломками на развитие умственных способностей у человека.

Перспектива

Спасибо за внимание!

Список используемых источников

• http://razvitiedetei.info/dosug/geometricheskij-konstruktor-tangram.html- Детский сайт для родителей. Развитие детей. https://ncuxolog.ru/zagadochnyj-tangram- Мир детских эмоций и чувств. http ://fb.ru/article/173523/kolumbovo-yaytso-uvlekatelnaya-golovolomka-dlya-detey-i-vzroslyih - Fb.ru http :// novijmir . blogspot . ru /- Волшебная шкатулка. Занимательная математика. http:// coollib.com/i/85/290985/i_025.jpg - слайд №7 https:// im2-tub-ru.yandex.net/i?id=1c4b6a17084cf5d65390c7df921d0aaf-l&n=13 , http :// www.born-today.com/images/3355.jpg - слайд 9
• http://razvitiedetei.info/dosug/geometricheskij-konstruktor-tangram.html- Детский сайт для родителей. Развитие детей.
• https://ncuxolog.ru/zagadochnyj-tangram- Мир детских эмоций и чувств.
• http ://fb.ru/article/173523/kolumbovo-yaytso-uvlekatelnaya-golovolomka-dlya-detey-i-vzroslyih - Fb.ru
• http :// novijmir . blogspot . ru /- Волшебная шкатулка. Занимательная математика.
• http:// coollib.com/i/85/290985/i_025.jpg - слайд №7
• https:// im2-tub-ru.yandex.net/i?id=1c4b6a17084cf5d65390c7df921d0aaf-l&n=13 , http :// www.born-today.com/images/3355.jpg - слайд 9