Формирование навыков самостоятельной деятельности учащихся на уроках математики на основе деятельностного подхода

Формирование навыков самостоятельной деятельности

учащихся на уроках математики

на основе деятельностного подхода

(слайд 1)

С дидактической точки зрения основу деятельностного подхода составляет самостоятельная работа учащихся, направленная на творческий поиск и постоянное созидание нового.

В соответствии с уровнем самостоятельной деятельности можно выделить типы самостоятельных работ: воспроизводящие, реконструктивно-вариативные, эвристические, творческие. В практике каждый тип самостоятельной работы представлен большим разнообразием видов работ.

(слайд 2)

Наиболее распространенные и эффективные: работа с книгой, упражнения, проверочные самостоятельные работы. В презентации отражено развитие умений учащихся работать с учебным математическим текстом.

(слайд 3)

Предлагаю Вашему вниманию дидактические условия работы с учебником.

Работая с математическим текстом, учимся находить ответы на вопросы, составлять алгоритмы решения задач по образцу, выделять смысловые опорные пункты, читать графики.

(слайд 4)

Как организую работу, например, при изучении десятичных дробей в 5 классе?

Чтобы подготовить учащихся к восприятию нового материала, провожу устную работу (с записью ответов в тетрадь).

(слайд 5)

Проверяя ответы, предлагаю отгадать зашифрованное слово.

Затем выписываем отдельно дроби со знаменателями 10, 100, 1000.

Задаю вопросы: можно ли эти дроби записать без знаменателя? Как это сделать? Как эти дроби называются?

Заслушиваю мнения учащихся. Затем правильные ответы на вопросы находим в учебнике. Записываем обыкновенные дроби в виде десятичных. После этого выполняем упражнения на закрепление.

На этом же уроке даю д/з: прочитать п. 3.1 «Сравнение десятичных дробей» и ответить на вопросы в конце пункта. А следующий урок начинаю с анализа текста: - Изменится ли дробь, если в конце ее приписать 0? 4 нуля? 9 нулей? Приведите примеры. – Как сравнивать десятичные дроби? Покажите на примерах.

(слайд 6)

Изучая в 9 классе тему «Вероятность равновозможных событий (п. 35), это новая тема в содержании образовательного стандарта, я предложила учащимся прочитать текст этого пункта дома, разобрать примеры и ответить на контрольные вопросы.

На следующем уроке мы повторили теоретический материал, выполнили упражнения на закрепление, проверили умения решать задачи по данной теме.

Д/з тест 23, КИМы.

«Начальные сведения из теории Вероятностей»

(слайды 7-31)

Упражнения являются наиболее распространенным видом самостоятельной работы. Их роль при осмыслении и закреплении знаний, развитии мышления исключительно велика. В качестве примера приведу работу по выводу формулы суммы углов выпуклого n-угольника. Для этого учащиеся самостоятельно составляют таблицу, итогом служит получение формулы.

(слайды 32, 33)

Самостоятельные работы на закрепление и применение пройденного материала выполняют функцию формирования определенных навыков, в том числе вычислительных.

Вызывают интерес задания-лабиринты. Простым вариантом этого задания является решение упражнений (чаще однотипных), когда ученики сверяют свои ответы с выписанными на доске (не по порядку). Это позволяет работать в индивидуальном темпе и сразу получить результаты.

Так, при закреплении темы «Линейное уравнение с одной переменной» предлагается расшифровать пословицу.

(слайд 34)

Очень нравится ребятам отгадывать зашифрованные слова. Они и сами составляют подобные задания. Приведу примеры карточек: «Сложение и вычитание десятичных дробей» (5 класс), «Умножение обыкновенных дробей» (6 класс). Такие задания даю при обобщение и систематизации знаний по теме или разделу.

(слайды 35 - 38)

Письменную самостоятельную работу рассматривают как один из способов организации самостоятельной деятельности учащихся. Такие работы предполагают большую самостоятельность ребят, при фронтальном проведении их выявляется уровень общей подготовки класса и каждого ученика в отдельности.

(слайд 39)

Большую помощь в организации самостоятельной деятельности оказывают мне дидактические и контрольно-измерительные материалы, издаваемые по всем классам. Тесты КИМов тематически сгруппированы, соответствуют требованиям школьной программы и возрастным особенностям учащихся. Структура КИМов аналогична структуре тестов в формате ЕГЭ. В конце пособия предложены тексты самостоятельных и контрольных работ, а также ключи к тестам (при выполнении заданий требую решения). Анализируя результаты, считаю, что применение различных видов самостоятельной работы позволяет увеличить возможность каждому ученику овладеть учебным материалом с учетом личных особенностей. Организация самостоятельной работы стимулирует процесс обучения, создает интерес и положительное отношение ребят к математике. Очень приятно и радостно слышать, когда дети говорят: «Лучше пусть будет еще один урок математики, чем какой-либо другой предмет».

Список литературы

1. Виленкин Н.Я. Математика 5 класс. Учебник для общеобразовательных учреждений. – Мнемозина: Москва, 2013.

2. Макарычев Ю. Н. Алгебра 9 класс. – Просвещение: Москва, 2013.

3. Маркова В.В. Современный урок математики: дидактические основы и конструирование урока. – Киров, 2010.

4. Элементы комбинаторики, статистики и теории вероятностей в курсе математики основной школы. Методическое пособие под ред. В.И. Марковой. – Киров, 2004г.

Формирование навыков самостоятельной деятельности учащихся на уроках математики на основе деятельностного подхода

Работу выполнила

Василькова Нина Николаевна

учитель математики

МКОУ ООШ д. Зайцевы

2016 год

Особенности деятельностного подхода:

• - знания добываются, создаются учеником в процессе личной работы (под руководством учителя), а не сообщаются ему в готовом виде;
• - учебный процесс выстраивается на постепенном усложнении содержания, способа и характера деятельности учащихся, на систематическом включении разных творческих заданий, необходимых для формирования личности ученика, его качеств и умений;
• - учитываются индивидуальные особенности учащихся и их субъективный опыт;
• - ведется обучение умениям работать с алгоритмами.

Деятельностный подход в обучении как средство достижения нового качества образования можно рассматривать с разных точек зрения: методологической, дидактической, психологической и методической.

С точки зрения дидактической основу деятельностного подхода составляет самостоятельная работа учащихся, направленная на творческий поиск и постоянное созидание нового.

Виды самостоятельной деятельности учащихся на уроках математики

• Работа с учебником.

• Выполнение упражнений.

• Письменные самостоятельные работы

Дидактические условия организации работы с учебником:

• тщательно планировать работу, подбирать удачные темы для самостоятельного чтения;
• четко управлять действиями учеников : что читать, с какой целью, на какие вопросы отвечать, какие упражнения выполнять после чтения;
• работа с учебником не должна занимать весь урок, она должна разумно сочетаться с другими видами учебной деятельности;
• широко использовать графический материал учебника для самостоятельной работы;
• обобщать и систематизировать материал.

Тема урока «Десятичная запись дробных чисел» (5 класс) Устная работа ( с записью ответов в тетрадь)

• № 1. Замените частное дробью или смешанным числом :

• № 2. Выразите в дециметрах

• 5 : 11
• 8 : 100
• 17 : 10
• 24 : 100
• 3 : 1000

6. 3м 2дм

7. 10м 3дм

8. 2см

9. 14дм 5см

10. 10см

Отгадайте зашифрованное слово:

8

100

Е

24

100

Я

2

10

Н

32

И

5

11

103

Д

Ч

1

7

10

С

14

Ы

5

10

3

100 0

1

Т

Е

• Выпишем отдельно дроби со знаменателями 10, 100, 1000
• Правильные ответы на вопросы находим в учебнике .
• Записываем обыкновенные дроби в виде десятичных.

– ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ СЛУЧАЙНОГО СОБЫТИЯ.

ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО ЗНАЧЕНИЯ ВЕРОЯТНОСТИ СОБЫТИЯ:

А – некоторое событие,

m – количество благоприятных исходов,

n – конечное число равновозможных исходов.

P – обозначение происходит от первой буквы французского слова probabilite – вероятность.

Классическое определение вероятности было впервые дано в работах французского математика Лапласа.

Пьер-Симо́н Лапла́с

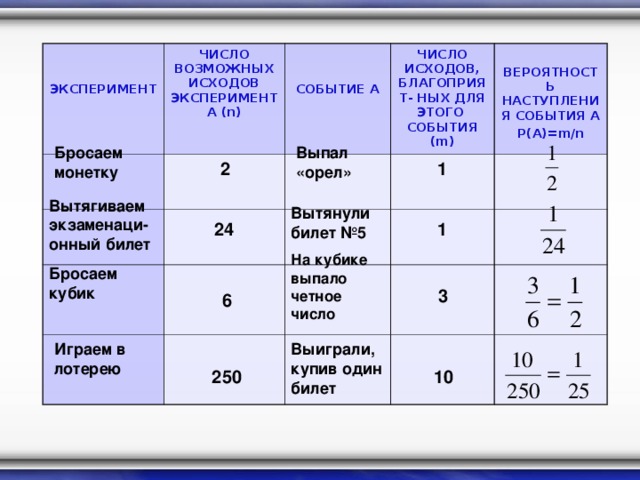
ЭКСПЕРИМЕНТ

ЧИСЛО ВОЗМОЖНЫХ ИСХОДОВ ЭКСПЕРИМЕНТА ( n)

СОБЫТИЕ А

ЧИСЛО ИСХОДОВ, БЛАГОПРИЯТ- НЫХ ДЛЯ ЭТОГО СОБЫТИЯ ( m)

ВЕРОЯТНОСТЬ НАСТУПЛЕНИЯ СОБЫТИЯ А

Р(А)= m / n

Выпал «орел»

Бросаем монетку

2

1

Вытягиваем экзаменаци- онный билет

Вытянули билет №5

1

24

На кубике выпало четное число

6

3

Бросаем кубик

Выиграли, купив один билет

Играем в лотерею

250

10

Пример 1

В школе 1300 человек, из них 5 человек хулиганы.

Какова вероятность того, что один из них попадётся директору на глаза?

Вероятность:

P ( A ) = 5/1300 = 1/250.

Пример 2.

При игре в нарды бросают 2 игральных кубика. Какова вероятность того, что на обоих кубиках выпадут одинаковые числа?

Составим следующую таблицу

1

1

2

11

2

3

12

21

3

31

22

4

4

13

5

32

14

5

41

23

24

6

42

51

33

6

15

52

34

16

43

25

61

26

53

44

35

62

54

36

45

63

55

64

46

56

65

66

Вероятность: P(A)=6/36 = = 1/6 .

Пример 3.

Из карточек составили слово «статистика». Какую карточку с буквой вероятнее всего вытащить ? Какие события равновероятные ?

Всего 10 букв.

Буква «с» встречается 2 раза –

P (с) = 2 / 10 = 1 / 5;

буква «т» встречается 3 раза –

P( т) = 3 / 10;

буква «а» встречается 2 раза –

P( а) = 2 / 10 = 1 / 5;

буква «и» встречается 2 раза –

P( и) = 2 / 10 = 1 / 5;

буква «к» встречается 1 раз –

P( к) = 1 / 10.

Свойства вероятности

• Вероятность достоверного события равна

• Вероятность невозможного события равна

• Вероятность события А не меньше , но не больше

?

1

?

0

?

?

1

0

• P(А) = 1 (u – достоверное событие);
• P(А) = 1 (u – достоверное событие);

• P(А) = 0 (v – невозможное событие);
• P(А) = 0 (v – невозможное событие);

• 0  P(A)  1.
• 0  P(A)  1.

Самостоятельная работа

Решение вероятностных задач

Задачи на вероятностную оценку случайного события

Задача 1.

В коробке 4 синих, 3 белых и 2 желтых фишки. Они тщательно перемешиваются, и наудачу извлекается одна из них. Найдите вероятность того, что она окажется: а) белой; б) желтой; в) не желтой. 

а) Мы имеем всевозможных случаев 9. Благоприятствующих событий 3. Вероятность равна:

P=3:9=1/3=0,33(3)

б) Мы имеем всевозможных случаев 9. Благоприятствующих событий 2. Вероятность равна P=2:9=0,2(2)

в) Мы имеем всевозможных случаев 9. Благоприятствующих событий 7 (4+3). Вероятность равна P=7:9=0,7(7)

Задача 2.

В коробке лежат 10 одинаковых шаров, на каждом из которых написан его номер от 1 до 10. Найдите вероятность следующих событий: а) извлекли шар № 7; б) номер извлеченного шара – четное число; в) номер извлеченного шара кратен 3.  

Всевозможных событий 10.

Вероятность того, что выпадет шар под №7 - 1/10.

5 благоприятных событий выпадения шара с четным номером, а вероятность 5/10=1/2.

3 благоприятных события выпадения шара с номером, кратным трем, вероятность равна 3/10

Задача 3.

Мальчики играли в “Орлянку”. Но монетка куда-то закатилась. Предложите, как заменить ее игральным кубиком?

Считать "орел" -  четное число, а "решка" – нечетное число.  

Задача 4 .

В настольной игре сломалась вертушка с тремя разными секторами: красным, белым и синим, но есть кубик. Как заменить вертушку? 

Считать на кубике 1 и 2 - красный сектор, 3 и 4 - синий сектор, 5 и 6 - белый сектор.

Задания для самостоятельной работы

Задача 1 . В урне находятся 3 синих, 8 красных и 9 белых шаров одинакового размера и веса, неразличимых на ощупь. Шары тщательно перемешаны. Какова вероятность появления синего, красного и белого шаров при одном вынимании шара из урны?

Задача 2 . Наташа купила лотерейный билет, который участвует в розыгрыше 100 призов на 50000 билетов, а Лена – билет, который участвует в розыгрыше трех призов на 70000. У кого больше шансов выиграть?

Задание 3 . В настольной игре потеряли кубик. Как заменить его с помощью разноцветных фишек?

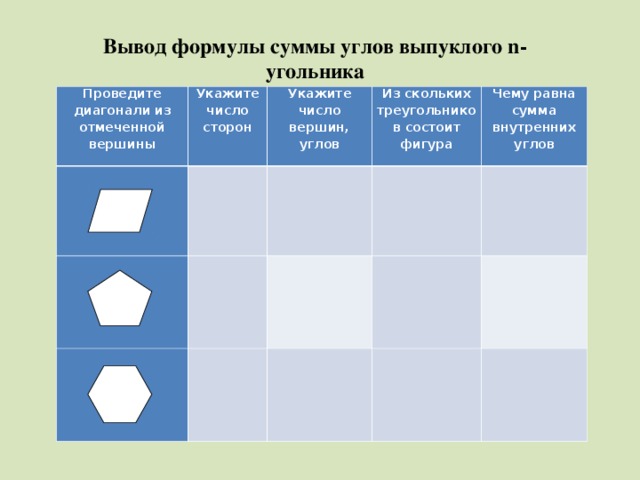
Вывод формулы суммы углов выпуклого n-угольника

Проведите диагонали из отмеченной вершины

Укажите число сторон

Укажите число вершин, углов

Из скольких треугольников состоит фигура

Чему равна сумма внутренних углов

.

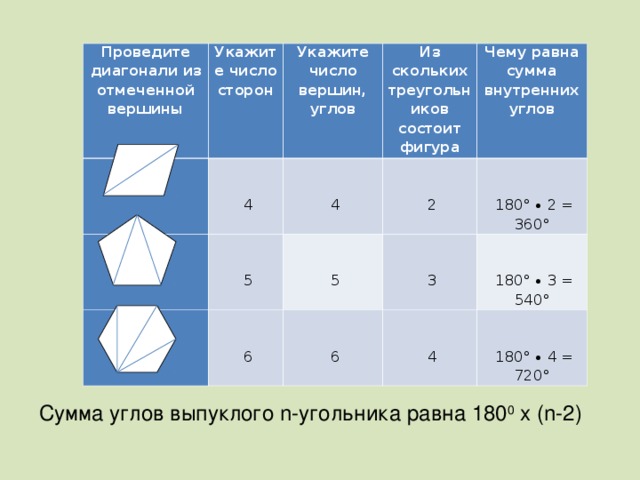
Проведите диагонали из отмеченной вершины

Укажите число сторон

  4

Укажите число вершин, углов

  5

  4

Из скольких треугольников состоит фигура

  2

  6

Чему равна сумма внутренних углов

  5

  180° ∙ 2 = 360°

  3

  6

  4

  180° ∙ 3 = 540°

  180° ∙ 4 = 720°

Сумма углов выпуклого n -угольника равна 180 0 х ( n -2)

0,5Х = 1,2

А

5

Г

Д

-2

Е

-12

З

2,4

-1/3

К

Л

-4

О

36

Р

13,5

-0,8

У

-10

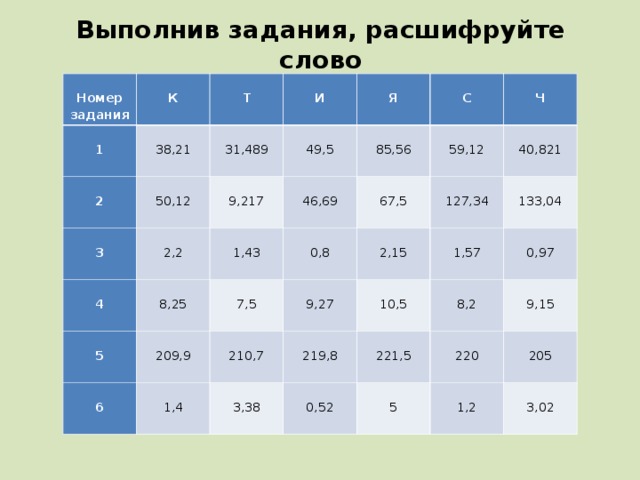
Выполнив задания, расшифруйте слово

Номер задания

1

К

Т

2

38,21

50,12

31,489

И

3

49,5

Я

9,217

4

2,2

С

85,56

46,69

1,43

8,25

5

67,5

59,12

Ч

209,9

7,5

6

0,8

127,34

40,821

2,15

9,27

210,7

1,4

133,04

10,5

3,38

219,8

1,57

0,97

0,52

221,5

8,2

220

9,15

5

205

1,2

3,02

• 35,85 + 4,971
• 125,19 – 78,5

3. x – 0,07 = 1,5

4. 9 – y = 1,5

5. Ученики четвертого класса собрали 215,7 кг металлолома, а пятого класса на 5,8 кг больше. Сколько металлолома собрал 5 класс?

6. Скорость лодки в стоячей воде 3,2 км/ч, а скорость течения 1,8 км/ч. Найдите скорость против течения реки.

№

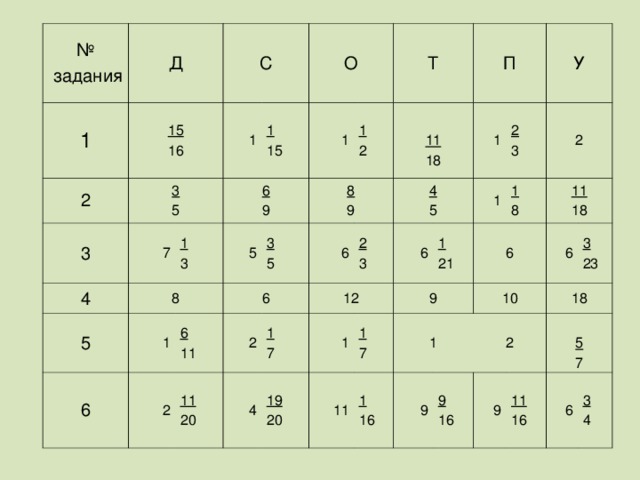
задания

Д

1

2

15

16

3

3

5

С

7

4

1

8

6

9

1

15

1

3

О

5

5

6

1

1

8

9

2

1

2

3

5

6

11

6

Т

6

2

11

20

11

18

2

3

4

5

1

7

П

12

4

1

1

19

20

6

11

1

7

1

21

1

2

3

У

9

6

1

8

2

1

16

1

11

18

9

10

6

2

9

16

9

18

3

23

5

7

11

16

6

3

4

=

1

2

4

3

8

2

Признаки самостоятельной работы

Под самостоятельной работой учащихся понимается такая работа, которая выполняется по заданию учителя без непосредственной его помощи (но под его руководством) в специально отведенное для этого время.

Признаки самостоятельной работы:

• наличие цели работы;
• наличие конкретного задания;
• четкое определение формы выражения результата;
• обязательное выполнение задания каждым учеником;
• обязательное подведение итогов самостоятельной работы;
• самостоятельная работа определена во времени.

Отсутствие хотя бы одного признака уже не характеризует эту работу как самостоятельную.