ЦЕЛЬ: Повторить знания по теме «Линейная функция». Ввести понятие о взаимном расположении графиков линейных функций; научить находить координаты точки пересечения графиков.
Развитие интереса к предмету, познавательных качеств, инициативы, мышления.
Воспитание положительного отношения к знаниям, дисциплинированности, взаимоподдержки и взаимопомощи при работе в группах.
ХОД УРОКА:
1. Проверка домашнего задания.
«О, сколько нам открытий чудных, готовит просвещенья дух».
А.С.Пушкин
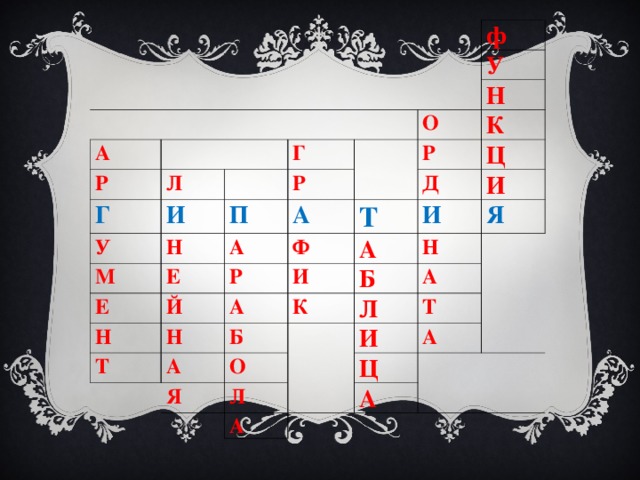
- А какое открытие совершили вы, ребята, разгадав дома кроссворд? Какое было зашифровано слово? /ГИПАТИЯ/
-Кто узнал, что означает это слово?
ГИПАТИЯ (370 – 415) – первая, известная в истории – женщина – математик. Руководитель группы александрийских учёных, она была растерзана по наущению христианских священников. Её годы жизни совпали с упадком значения Александрии как главного центра науки того времени.
- А теперь проверяем кроссворд.
1) Независимая переменная.
2) Вид функции.
3) Кривая.
4) Множество точек координатной плоскости, удовлетворяющее некоторому условию.
5) Способ задания функции.
6) Одна из координат точки.
7) Зависимость.
ф
У
Н
О
К
А
Г
Р
Ц
Р
Л
Р
Д
И
Г
И
П
А
Т
И
Я
У
Н
А
Ф
А
Н
М
Е
Р
И
Б
А
Е
Й
А
К
Л
Т
Н
Н
Б
И
А
Т
А
О
Ц
Я
Л
А
А
2. Сегодня на уроке мы совершим немало открытий, отправившись в путешествие на Луну.
Но любое путешествие требует подготовки, проверим, как вы готовы.
1) На каком рисунке изображён график функции?
а) б) в)
2) Какими формулами заданы линейные функции?
а) у = 5х – 7; д) у = х/4;
б) у = 2х2 + 3; е) у = 8;
в) у = 0·х + 1; ж) у = 2/х – 2;
г) у = - 2х + 3; з) у = 100х.
3) Выясните, принадлежит ли графику функции у = - 3х + 6 точка:
а) А( 2; 0); б) В( 3; 3); в) С( 4; -6)?
3. Любое путешествие имеет перед собой определённые цели.
Для того, чтобы определить наши цели, решим анаграммы.
ФФИИЦЭОКТНЕ (КОЭФФИЦИЕНТ)
АЯРПЯМ (ПРЯМАЯ)
АДЧААЗ (ЗАДАЧА)
АНЯИЛНЕЙ КЦНУФЯИ (ЛИНЕЙНАЯ ФУНКЦИЯ)
Исключите лишнее слово (задача). Что объединяет остальные слова?
Мы совершим путешествие по известным функциям, в ходе которого узнаем, как могут взаимно располагаться графики линейных функций и как найти координаты точки пересечения графиков.
4. В путешествие отправляются два корабля (две группы).
Все корабли начинают старт с разных точек земной поверхности, но приземлиться должны в одном месте на Луне, заданном координатами ( 2; 4). Задайте формулой у = кх + в движение своего корабля, если в1 = 0; в2 = 2; Постройте график своего движения.
Штурманы каждого корабля пишут полученную формулу на доске. Командиры выводят свои корабли на орбиту. Графики всех функций пересеклись в одной точке, значит мы удачно прилунились.
5. А теперь проведём исследовательскую работу.
Каждому экипажу даётся задание:
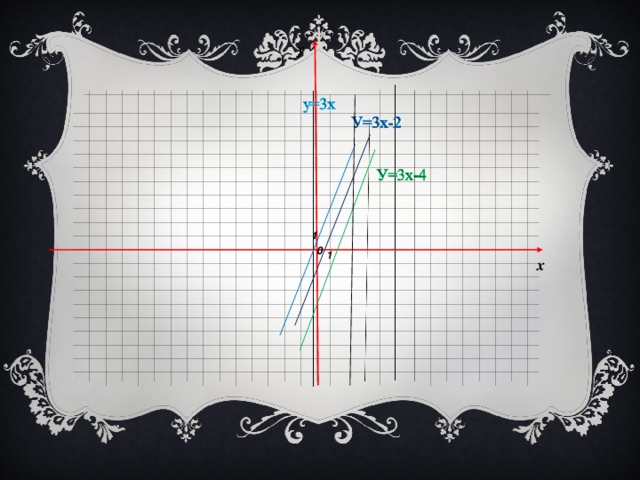
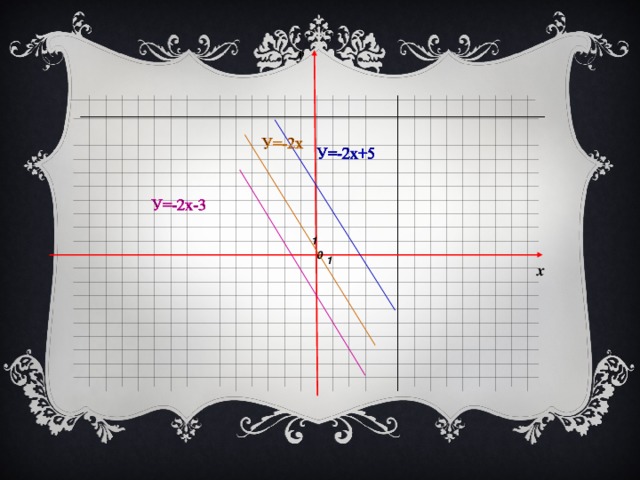
1) Водной координатной плоскости построить графики функций: 1). у = 3х; у = 3х – 4; у = 3х +2. 2) у = 5х; у = 5х – 1; у = 5х +3. Как расположены графики данных функций?
- Сравните коэффициенты при х.
Сделаем вывод: если коэффициенты при х одинаковы, то графики функций, заданных формулами вида у = кх + в, параллельны.
2) В одной координатной плоскости построить графики функций
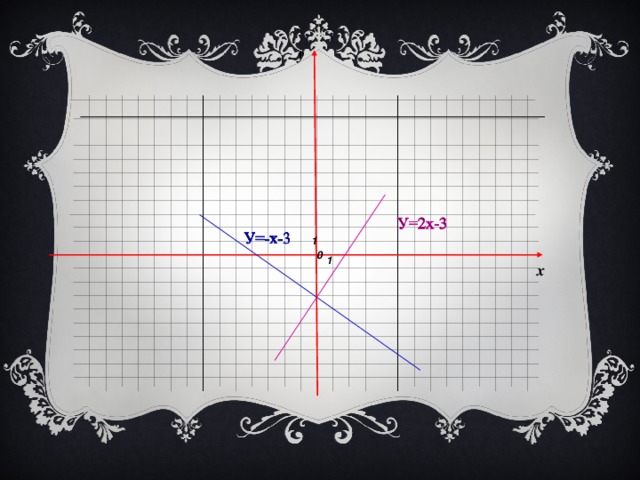
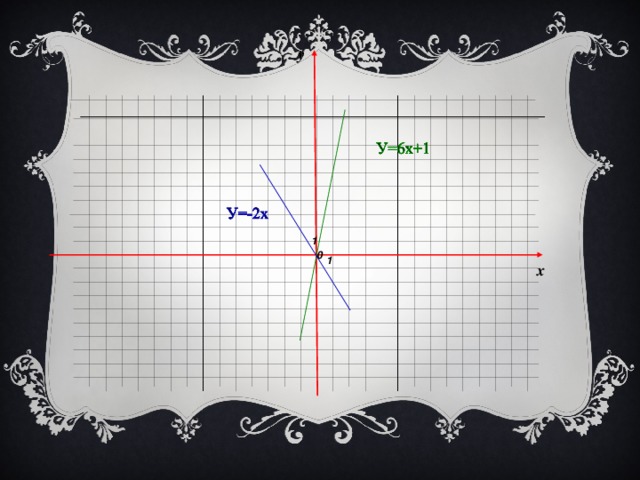
1). у = - х – 3 и у = 2х +3. 2). у = 6х + 1 и у = -2х. Как расположены графики этих функций?
- Сравните коэффициенты при х.
Сделаем вывод: если коэффициенты при х различны, то графики функций, заданных формулами вида у = кх + в, пересекаются.
Для закрепления выполним
3)Найдите по графику (1) координаты точки пересечения графиков функций у = -х – 3 и у = 2х + 3.
Мы нашли такое значение х, которому соответствует одно и то же значение у. А( -2; -1).
Как найти координаты этой точки, не выполняя построения?
Нужно решить уравнение, приравняв правые части формул. В результате мы найдём абсциссу точки пересечения.(х) А как найти ординату (у)? Подставить в одну из формул найденное значение х.
Найдём таким способом координаты точки пересечения графиков функций (1) и (2).
6. Пора возвращаться домой. На обратном пути, движения кораблей будет задано формулами:
у = 10х – 8; у = -3х +5;
Все два корабля должны приземлиться в точке ( х; у), координаты которой вы и найдёте.
1 экипаж 2 экипаж
у = 10х – 8 у = -3х + 5
у = -3х + 5 у = 5х – 3
В какой же точке мы приземлились? (1; 2).
7. Мы удачно добрались до Земли, где нас встречают родные и близкие.
Но, тем не менее, нужно провести разбор полётов:
- В каком случае графики линейных функций параллельны?
- Когда графики двух линейных функций пересекаются?
- Как найти координаты точки пересечения графиков?
8. Дома вы попытаетесь ещё раз проделать этот маршрут, построив график функции y = 0,5x + 3.
Какие значения принимает функция, если 0 ≤ х ≤ 8?
9. За удачное выполнение космических программ оценкой «отлично» награждаются…..... а
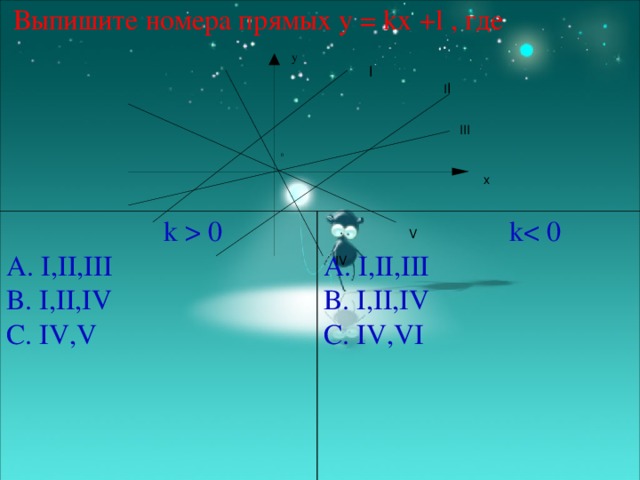0 A. I,II,III B. I,II,IV C. IV,V kA. I,II,III B. I,II,IV C. IV,VI у I I I III 0 х V IV" width="640"
