Разработка позволит обобщить и систематизировать теоретический материал по теме «Прогрессии».
Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.
Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским ученым. Индийский математик АРИАБХАТТА(5в.) применял формулы общего члена и суммы арифметической прогрессии.
Но правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении «Книга абака» в 1202 г (ЛЕОНАРДО ПИЗАНСКИЙ).
- Сами по себе прогрессии известны так давно, что, конечно, нельзя говорить о том, кто их открыл. Уже в Древнем Египте знали не только арифметическую, но и геометрическую прогрессию. Об этом свидетельствует приведенная ниже задача из папируса АХМЕСА:
- «У семи лиц по семи кошек; каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?»
Эта задача много раз с разными вариациями повторялась и у других народов в другие времена. Например, в написанной в XIII в. «Книге об абаке» Леонардо Пизанского (Фибоначчи) есть задача, в которой фигурируют 7 старух, направляющихся в Рим (очевидно, паломниц), у каждой из которых 7 мулов, на каждом из которых по 7 мешков, в каждом из которых по 7 хлебов, в каждом из которых по 7 ножей, каждый из которых в 7 ножнах. В задаче спрашивается, сколько всего предметов.
И на Руси решались похожие задачи. Еще в XIX веке в деревнях загадывали: “Шли 7 старцев. У каждого старца по 7 костылей. На каждом костыле по 7 сучков. На каждом сучке по 7 кошелей. В каждом кошеле по 7 пирогов. В каждом кошеле по 7 воробьев. Сколько всего?” А ведь это та же задача Прожившая тысячелетия она сохранилась почти неизменной.
В старинной книге «Арифметики МАГНИЦКОГО мы находим следующую забавную задачу: Один крестьянин продавал лошадь за 156 рублей. Покупатель, уже почти купивший лошадь, затем раздумал и вернул ее хозяину, сказав при этом: Нет мне расчета покупать за эту цену лошадь, которая таких денег не стоит. Тогда крестьянин предложил другие условия:
- Если по-твоему цена лошади высока, то купи только ее подковные гвозди, лошадь получишь бесплатно в придачу. Гвоздей в каждой подкове 6. За первый гвоздь дай мне всего четверть копейки, за второй –половину копейки, за третий – 1 копейку и т.д. Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условия продавца, рассчитывая, что за гвозди придется заплатить не более 10 рублей. На сколько покупатель проторговался? Ответ: За 24 подковных гвоздя пришлось заплатить 42000р, т.е. покупатель проторговался. За такую цену необидно и лошадь дать в придачу.
Легенда о шахматной доске.
Шахматы – одна из самых древних игр. Она существует уже многие века, и неудивительно, что с нею связаны различные предания, правдивость которых, за давностью времен, невозможно проверить.
Шахматная игра была придумана в Индии. Когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений шахматных фигур. Узнав, что игра была изобретена одним из его подданных, царь призвал его к себе ее изобретателя, ученого Сету, чтобы достойно вознаградить его. Он сказал, что достаточно богат, чтобы выполнить любое желание ученого.
Сета попросил царя выдать за первую клетку шахматной доски одно пшеничное зерно, за вторую – 2 зерна, за третью - 4, за четвертую – 8, за пятую – 16 и т.д.
Сможет ли царь Шерам выполнить желание Сеты?
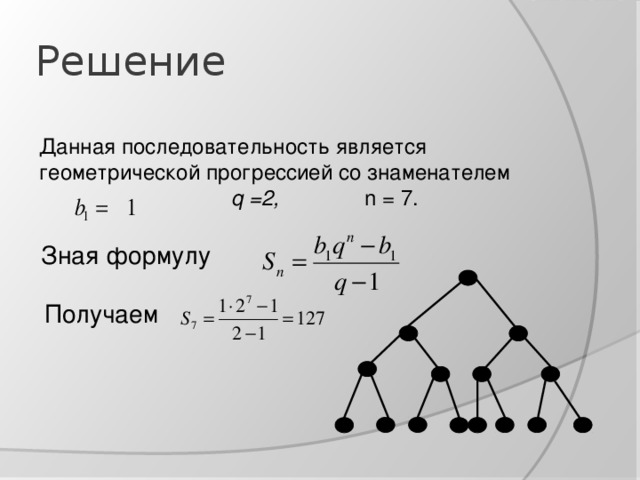
Ответ: Понятно, что нам придется находить сумму 64 членов геометрической прогрессии
1 + 2 + 4 + 8 + 16 + … здесь b1 = 1, q = 2, n = 64
(18 квинтиллионов 446 квадриллионов 744триллиона 73бмиллиарда 709 миллионов 551 тысяча 615).
все пшеничные зерна весят больше триллиона тонн. Это превосходит количество пшеницы, собранной человечеством до настоящего времени.
Если бы Шераму очень уж захотелось выполнить желание Сеты, то ему пришлось бы превратить земные царства в пахотные поля, осушить моря и океаны, растопить льды и снега, покрывающие далекие северные пустыни и засеять все это пространство пшеницей. Тогда, пожалуй, лет за пять он смог бы расплатиться с Сетой.
Чтобы представить себе, как велико это количество, можно прикинуть какой величины амбар потребовалось бы построить, чтобы поместить это зерно. Амбар должен быть шириной 10м, высотой 4м и длиной 3000000000км, а это в 2 раза дальше, чем от Земли до Солнца!.
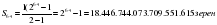
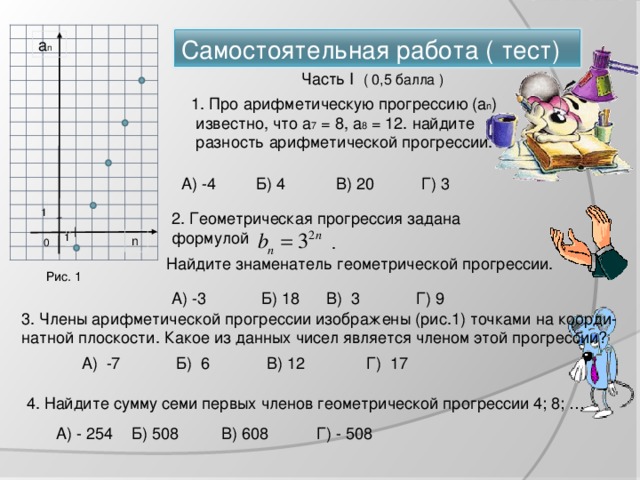
0 ) Ответ: b 5 = 72 (задания на 3 балла) 7. Сумма второго и пятого членов арифметической прогрессии равна 11. Третий её член на 6 больше первого. Найдите второй и четвёртый члены. Ответ: а 2 =1; а 4 = 7, Количество набранных баллов 1,5 - 2 оценка 2,5 – 4,5 «3» «4» 5 – 7,5 «5»" width="640"
