Табличный процессор Excel в изучении темы "Прогрессии"

Метапредметные связи в процессе изучения темы «Прогрессии»

Уроки 1 -2. “Числовая последовательность”

На данном уроке, объясняя рекуррентный способ задания последовательности, нужно привести в пример последовательность Фибоначчи. Для этого нужно рассказать о задаче, которая размещена в сочинении “Книга абака”, переработанной математиком Леонардо Фибоначчи.

"Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения".

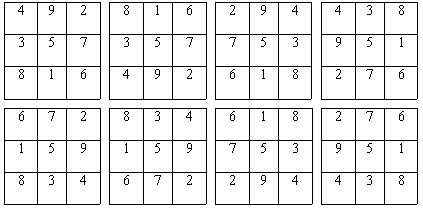
Можно предложить одну из этих схем для того, чтоб представить количество кроликов в каждый месяц.

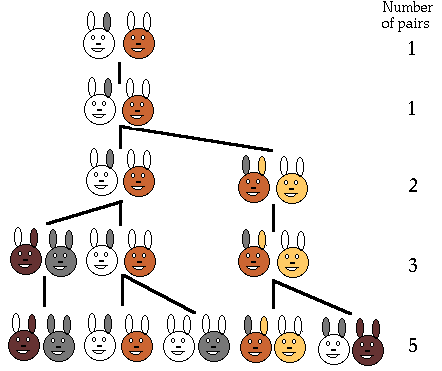
Ясно, что если считать первую пару кроликов новорожденными, то на второй месяц мы будем по прежнему иметь одну пару; на 3-й месяц - 1+1=2; на 4-й - 2+1=3 пары (ибо из двух имеющихся пар потомство дает лишь одна пара); на 5-й месяц - 3+2=5 пар (лишь 2 родившиеся на 3-й месяц пары дадут потомство на 5-й месяц); на 6-й месяц - 5+3=8 пар (ибо потомство дадут только те пары, которые родились на 4-м месяце) и т. д.

Таким образом, если обозначить число пар кроликов, имеющихся на n-м месяце через Fk, то F1=1, F2=1, F3=2, F4=3, F5=5, F6=8, F7=13, F8=21 и т. д., причем образование этих чисел регулируется общим законом: Fn=Fn-1+Fn-2 при всех n2, ведь число пар кроликов на n-м месяце равно числу Fn-1 пар кроликов на предшествующем месяце плюс число вновь родившихся пар, которое совпадает с числом Fn-2 пар кроликов, родившихся на (n-2)-ом месяце (ибо лишь эти пары кроликов дают потомство).

Числа Fn , образующие последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи.

Биографию Фибоначчи можно разместить на стенде “Это интересно”, также здесь размещается информация о том, где встречается последовательность Фибоначчи, чем она интересна.

ФИБОНАЧЧИ (Леонардо из Пизы)
Fibonacci (Leonardo of Pisa),  ок. 1175–1250

Итальянский купец Леонардо из Пизы более известный под прозвищем Фибоначчи был первым из великих математиков Европы позднего Средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить. Леонардо из Пизы, известный как Фибоначчи,. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты. В молодости Леонардо много путешествовал, сопровождая отца в деловых поездках. Например, мы знаем о его длительном пребывании в Византии и на Сицилии. Во время таких поездок он много общался с местными учеными.

Жизнь и научная карьера Леонардо теснейшим образом связана с развитием европейской культуры и науки.

До эпохи Возрождения было еще далеко, однако история даровала Италии краткий промежуток времени, который вполне можно было назвать репетицией надвигающейся эпохи Ренессанса. Этой репетицией руководил Фридрих II, император Священной Римской империи. Воспитанный в традициях южной Италии Фридрих II был внутренне глубоко далек от европейского христианского рыцарства. Рыцарские турниры Фридрих II совсем не признавал. Вместо этого он культивировал математические соревнования, на которых противники обменивались не ударами, а задачами.

На таких турнирах и заблистал талант Леонардо Фибоначчи. Этому способствовало хорошее образование, которое дал сыну купец Боначчи, взявший его с собой на Восток и приставивший к нему арабских учителей. Встреча между Фибоначчи и Фредериком II произошла в 1225 году и была событием большой важности для города Пизы. Император ехал верхом во главе длинной процессии трубачей, придворных, рыцарей, чиновников и бродячего зверинца животных. Некоторые проблемы, которые Император поставил перед знаменитым математиком, подробно изложены в Книге абака. Фибоначчи, очевидно, решил проблемы, поставленные Императором, и навсегда стал желанным гостем при Королевском дворе. Когда Фибоначчи перерабатывал Книгу абака в 1228 году, он посвятил исправленную редакцию Фредерику II. Всего он написал три значительных математических труда: Книга абака, опубликованная в 1202 году и переизданная в 1228 году, Практическая геометрия, опубликованная в 1220 году, и Книга квадратур. По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, учили математику чуть ли не до времен Декарта. Как указано в документах 1240 года, восхищенные граждане Пизы говорили, что он был "рассудительный и эрудированный человек", а не так давно Жозеф Гиз, главный редактор Британской Энциклопедии заявил, что будущие ученые во все времена "будут отдавать свой долг Леонардо Пизанскому, как одному из величайших интеллектуальных первопроходцев мира". Но хотя он и был величайшим математиком средних веков, единственные памятники Фибоначчи - это статуя напротив Пизанской башни через реку Арно и две улицы, которые носят его имя, одна - в Пизе, а другая - во Флоренции.

Последовательность Фибоначчи

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

Числа Fn , образующие последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи.

Можно рассмотреть отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:

1:1 = 1.0000, что меньше фи на 0.6180

2:1 = 2.0000, что больше фи на 0.3820

3:2 = 1.5000, что меньше фи на 0.1180

5:3 = 1.6667, что больше фи на 0.0486

8:5 = 1.6000, что меньше фи на 0.0180

По меpе нашего пpодвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим пpиближением к недостижимому "фи".

Следует обратить внимание, что в природе встречается именно приближение к числу "фи", тогда как математика оперирует с "чистым" значением. Его ввел Леонардо да Винчи и назвал "золотым сечением" (золотая пропорция). Cpеди его совpеменных названий есть и такие, как "золотое среднее" и "отношение вертящихся квадратов". Золотая пропорция – это деление отрезка АС на две части таким образом, что большая его часть АВ относится к меньшей части ВС так, как весь отрезок АС относится к АВ, то есть: АВ:ВС=АС:АВ=Ф (точное иррациональное число "фи").

Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается обратная к 1.618 величина (1 : 1.618=0.618). Это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение - бесконечная дробь, у этого соотношения также не должно быть конца.

При делении каждого числа на следующее за ним через одно, получаем число 0.382.

1:0.382=2.618

Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235, 2.618 , 1.618, 0.618, 0.382, 0.236. Все они играют особую роль в природе и в частности в техническом анализе.

Просто удивительно, сколько постоянных можно вычислить пpи помощи последовательности Фибоначчи, и как ее члены проявляются в огромном количестве сочетаний. Однако не будет преувеличением сказать, что это не просто игра с числами, а самое важное математическое выражение природных явлений из всех когда-либо открытых.

Последовательность Фибоначчи — это не просто игра с числами, а самое важное математическое выражение природных явлений из всех когда-либо открытых.

Именно с ней связывают универсальность существующих в природе форм. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Последовательность Фибоначчи в биологии.

Если пересчитать лепестки некоторых наиболее распространенных цветов, - например, ириса с его 3 лепестками, первоцвета с 5 лепестками, крестовника с 13 лепестками, маргаритки с 34 лепестками и астры с 55 (и 89) лепестками, то и тут видна последовательность Фибоначчи.

С тех пор как Фибоначчи открыл свою последовательность, были найдены даже явления природы, в которых эта последовательность, похоже, играет немаловажную роль. Одно из них — филлотаксис (листорасположение) — правило, по которому располагаются, например, семечки в соцветии подсолнуха. Семечки упорядочены в два ряда спиралей, один из которых идет по часовой стрелке, другой против. И каково же число семян в каждом случае? 34 и 55. В 19 веке ученые заметили, что цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках и т. д. "упакованы" по двойным спиралям, завивающимся навстречу друг другу. При этом числа "правых" и "левых" спиралей всегда относятся друг к другу, как соседние числа Фибоначчи (13:8, 21:13, 34:21, 55:34). Многочисленные примеры двойных спиралей, встречающихся повсюду в природе, всегда соответствуют этому правилу.

Идеальный пример можно найти и в стеблях и цветах тысячели­стника. Каждая новая ветвь тысячелистника растет из пазухи, и от новой ветви растут новые ветви. Складывая старые и новые ветви, можно найти число Фибоначчи в каждой горизонтальной плоскости.

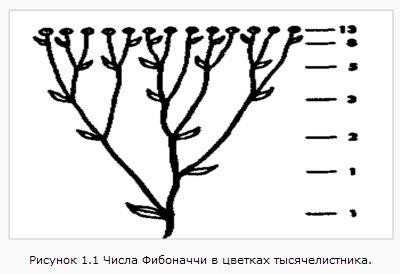
Если обратить внимание на то, как ветвится дерево, то тоже можно увидеть числа последовательности Фибоначчи.

Прямоугольник с шириной и высотой, равными двум соседним числам последовательности, представляет собой так называемый "Золотой прямоугольник", идеальный прямоугольник. Золотой прямоугольник можно разбить на более мелкие, с размерами, соответствующими соседним числам Фибоначчи. Если мы возьмем этот золотой прямоугольник и разобьем его на более мелкие в соответствии с последовательностью Фибоначчи и разделим каждый из них дугой, система начнет приобретать некую форму - мы увидим так называемую "Спираль Фибоначчи".

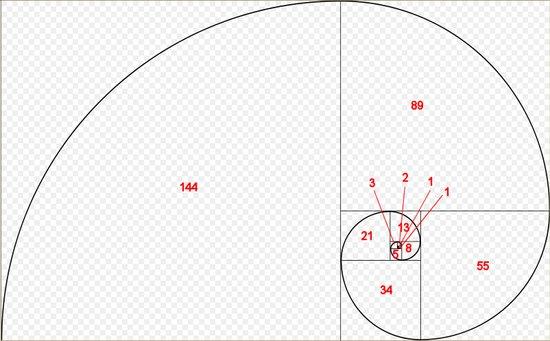
Эту удивительную спираль можем увидеть везде:

Алое многолистный

Сосновая шишка имеет 8 спиралей в одном направлении и 13 – в другом (8 и 13 идут друг за другом в последовательности Фибоначчи:

.

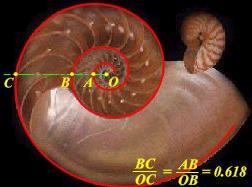
Раковина моллюска

Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль "кривой жизни".

Числа Фибоначчи проявляются в морфологии различных организмов. Например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13, 21, 34, 55. У хорошо знакомого комара - три пары ног, брюшко делится на восемь сегментов, на голове пять усиков - антенн. Личинка комара членится на 12 сегментов. Число позвонков у многих домашних животных равно 55.

Последовательность Фибоначчи в анатомии.

Друнвало Мелхиседек в книге "Древняя тайна Цветка Жизни" пишет: "Да Винчи вычислил, что, если нарисовать квадрат вокруг тела, потом провести диагональ от ступней до кончиков вытянутых пальцев, а затем провести параллельную горизонтальную линию (вторую из этих параллельных линий) от пупка к стороне квадрата, то эта горизонтальная линия пересечет диагональ точно в пропорции фи, как и вертикальную линию от головы до ступней. Если считать, что пупок находится в той совершенной точке, а не слегка выше для женщин или чуть ниже для мужчин, то это означает, что тело человека поделено в пропорции фи от макушки до ступней… Если бы эти линии были единственными, где в человеческом теле имеется пропорция фи, это, вероятно, было бы только интересным фактом. На самом деле пропорция фи обнаруживается в тысячах мест по всему телу, а это не просто совпадение. Вот некоторые явственные места в теле человека, где обнаруживается пропорция фи. Длина каждой фаланги пальца находится в пропорции фи к следующей фаланге… Та же пропорция отмечается для всех пальцев рук и ног. Если соотнести длину предплечья с длиной ладони, то получится пропорция фи, так же длина плеча относится к длине предплечья. Или отнесите длину голени к длине стопы и длину бедра к длине голени. Пропорция фи обнаруживается во всей скелетной системе. Она обычно отмечается в тех местах, где что-то сгибается или меняет направление. Она также обнаруживается в отношениях размеров одних частей тела к другим. Изучая это, все время удивляешься".

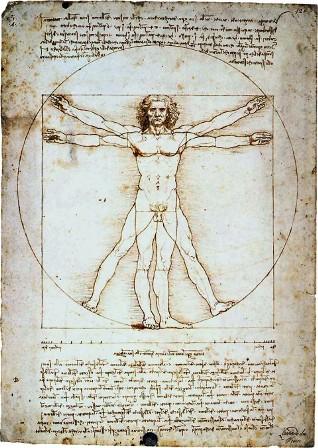
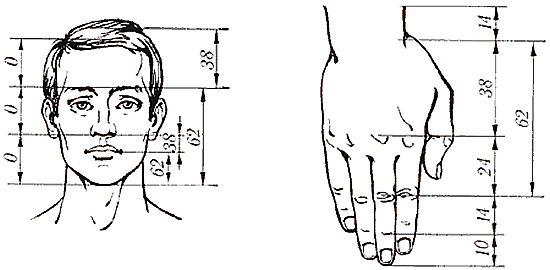
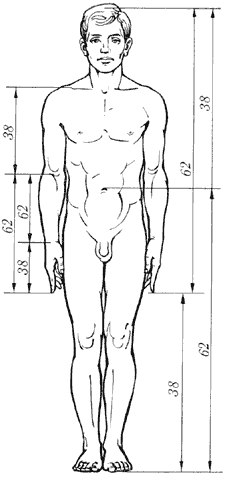
В анатомическом строении тела человека можно обнаружить немало "золотых пропорций", например длины фаланг пальцев. Обратите внимание на соотношения стопы и голени, голени и бедра, кисти и предплечья, верхней части плеча и лопатки, расстояний от макушки до бедра и до пятки.

Не меньше примеров "золотого сечения" встречается в лицевой эстетике. Идеальная пропорция наблюдается при сравнении ширины одной ноздри с суммарной шириной носовой перегородки и другой ноздри. Наиболее красивые лица также демонстрируют золотую прогрессию при сравнении ширины носа в области переносицы по внутренним краям орбит с шириной основания. Данная прогрессия продолжается далее к ширине ротовой щели, ширине между наружными углами глаз и, наконец, к ширине лба на уровне линии бровей.

Вертикальные пропорции имеют еще большее значение для создания симметрии лица. Эти пропорции берут начало от соотношения верхней и нижней губ: если за единицу принять высоту верхней губы, то у наиболее красивых губ высота нижней губы будет больше именно в идеальной пропорции.Еще одна идеальная вертикальная пропорция наблюдается, если за 1 принять высоту фильтрума или губного желобка (от "лука Купидона" до основания носа): в этом случае суммарная высота губ будет составлять 1,618.

У людей с красивыми лицами существует идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это явление называется "динамической симметрией" или "динамическим равновесием". Расстояние от линии смыкания губ до крыльев носа пропорционально расстоянию от линии губ до низшей точки подбородка в соотношении 1 : 1,618 (кончик носа при этом может быть приподнят или опущен, это не влияет на результат). Было также установлено, что расстояние от линии смыкания губ до крыльев носа идеально пропорционально расстоянию от зрачка глаза до крыла носа. Таким образом, на идеальном лице расстояние от глаз до крыльев носа равняется расстоянию от ротовой щели до подбородка (гармоническое уравнение).

Идеальная пропорция существует между расстояниями от линии роста волос (расположенной в верхней части лба в области начала апоневроза черепа) до зрачковой линии и от нее до подбородка. Если затем перевернуть циркуль, не изменяя положения его ножек, станет видно, что между расстояниями от нижней точки подбородка до крыльев носа и от крыльев носа до линии роста волос тоже идеальная пропорция. Эти данные показывают, что на идеальном лице в целом равны три вертикальных расстояния, вновь образующие гармоническое уравнение: (1) расстояние от линии роста волос до зрачковой линии, (2) расстояние от зрачковой линии до линии смыкания губ и (3) расстояние от крыльев носа до подбородка. Интересно, что на красивой голове даже высота уха тесно связана с этим размером.

Последовательность Фибоначчи в музыке

Эти числа, бесспорно, являются частью мистической естественной гармонии, которая приятно осязается, приятно выглядит и даже приятно звучит. Музыка, например, основана на 8-ми нотной октаве. На фортепьяно это представлено 8 белыми клавишами и 5 черными - всего 13.

Более наглядное представление можно получить, изучая спирали в природе и произведениях искусства. Сакральная геометрия исследует два вида спиралей: спираль золотого сечения и спираль Фибоначчи. Сравнение этих спиралей позволяет сделать следующий вывод. Спираль золотого сечения идеальна: у нет начала и нет конца, она продолжается бесконечно. В отличии от нее спираль Фибоначчи имеет начало. Все природные спирали – это спирали Фибоначчи, а в произведениях искусства используются обе спирали, иногда одновременно.

Последовательность Фибоначчи и архитектура пирамид.

Многие пытались разгадать секреты пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скоpее неразрешимая головоломка из числовых комбинаций. Замечательные изобpетательность, мастерство, время и труд аpхитектоpов пирамиды, использованные ими пpи возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была дописьменной, доиероглифической и символы были единственным средством записи открытий.

Ученые обнаружили, что три пирамиды в Гизе выстроены по спирали. В 1980-е годы было установлено, что там присутствуют и золотосеченная спираль и спираль Фибоначчи.

Kлюч к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.

Площадь тpеугольника

356 x 440 / 2 = 78320

Площадь квадpата

280 x 280 = 78400

Длина грани пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды -484.4 фута (147.6 м). Длина грани, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) - это числа из последовательности Фибоначчи.

Эти интересные наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618. Современные ученые склоняются к интерпретации, что древние египтяне построили ее с единственной целью - передать знания, которые они хотели сохранить для грядущих поколений. Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет центральную роль.

Не только египетские пирамиды построены в соответствии с совершенными пpопоpциями золотого сечения, то же самое явление обнаружено и у мексиканских пирамид. Возникает мысль, что как египетские, так и мексиканские пирамиды были возведены приблизительно в одно время людьми общего происхождения.

Многие пытались разгадать секреты пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скорее неразрешимая головоломка из числовых комбинаций. Замечательные изобретательность, мастерство, время и труд аpхитектоpов пирамиды, использованные ими при возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Kлюч к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.

Последовательность Фибоначчи и развитие человека

Развитие человека также происходит соответственно данной пропорции и подчиняется закону ее чисел, разделяя нашу жизнь на этапы с теми или иными доминантами механизма творчества.

Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет:

• 0 — начало отсчета — ребенок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;

• 1 — ребенок овладел ходьбой и осваивает ближайшее окружение;

• 2 — понимает речь и действует, пользуясь словесными указаниями;

• 3 — действует посредством слова, задает вопросы;

• 5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребенку охватить мир во всей его целостности;

• 8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии жизни;

• 13 — начинает работать механизм таланта, направленный на превращение приобретенного в процессе наследования материала, развивая свой собственный талант;

• 21 — механизм творчества приблизился к состоянию гармонии и делаются попытки выполнять талантливую работу;

• 34 — гармония мышления, чувств, воображения и психомоторики: рождается способность к гениальной работе;

• 55 — в этом возрасте, при условии сохраненной гармонии души и тела, человек готов стать творцом. И так далее...

Эта схема также может быть замечена вокруг нас и в нашей каждодневной жизни. Но самый потрясающий пример находится прямо над нашей головой на расстоянии приблизительно в 100 000 световых лет - даже спирали галактик сформированы по абсолютно тому же принципу, как и крошечные раковины...

Демонстрация ограниченности, монотонности, бесконечности последовательностей в табличном процессоре Excel..

Урок 3. “Числовая последовательность”

Рассмотреть последовательность Фибоначчи, заданную с помощью с копирования формулы с относительным адресом ячеек в табличном процессоре Excel

номер члена последовательности Фибоначчи	член последовательности Фибоначчи
1	1
2	1
3	=B2+B3
4	=B3+B4
5	=B4+B5
6	=B5+B6
7	=B6+B7
8	=B7+B8
9	=B8+B9
10	=B9+B10
11	=B10+B11
12	=B11+B12

Таким образом, моментально получаем таблицу значений, которую можно продолжать до любого номера последовательности.

номер члена последовательности Фибоначчи	член последовательности Фибоначчи
1	1
2	1
3	2
4	3
5	5
6	8
7	13
8	21
9	34
10	55
11	89
12	144

Урок 4-5 “Арифметическая и геометрическая прогрессии”.

На первом (4) уроке учащиеся обмениваются информацией по теме “Магические квадраты”. Подобный доклад может быть предложен кому – либо из учеников на предыдущем уроке, с которым он выступит перед классом. На втором уроке (5) составление квадрата с подобными свойствами из девяти последовательных членов арифметической прогрессии.

Магические квадраты

Древние люди куда больше зависели от природы, чем мы. Не имея метеорологических станций и спутников, центров для обработки наблюдений и прогнозирования, они предсказывали погоду по поведению птиц и животных, форме облаков, цвету восхода и заката Солнца. Найденные приметы передавались из поколения в поколение. Ими не пренебрегает и современная служба погоды.

Подобные приметы существовали не только для определения погоды, люди пытались найти связи для всех важных для них явлений с другими явлениями. Так родилась астрология, связывающая судьбы людей и народов с расположением небесных светил. А с появлением чисел им стали придавать и мистический смысл. До сих пор многие считают число 13 несчастливым, а уж если тринадцатое число месяца — пятница, то тут жди беды.

От беды нужно иметь защиту. Так появились разнообразные амулеты, предохраняющие человека от несчастий: драгоценные камни, когти и зубы животных, листья и травы. А в Китае и Индии с давних пор одним из видов амулета была бумажка с девятью цифрами, записанными в некотором порядке. (Цифры там были, конечно, не такие , которыми мы пользуемся сейчас, но имели то же числовое значение что и на данном квадрате)

4	9	2
3	5	7
8	1	6

Главное свойство такого расположения цифр в том, что их сумма в каждом горизонтальном ряду, в каждом вертикальном ряду и по каждой из двух диагоналей одна и та же.

Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.

По древней китайской легенде, император Ню, живший 4000 лет назад, однажды нашел на берегу реки священную черепаху, на панцире которой был изображен рисунок, состоящий из черных и белых кружков, соединенных черточками. Этот рисунок назвали “ло-шу”.

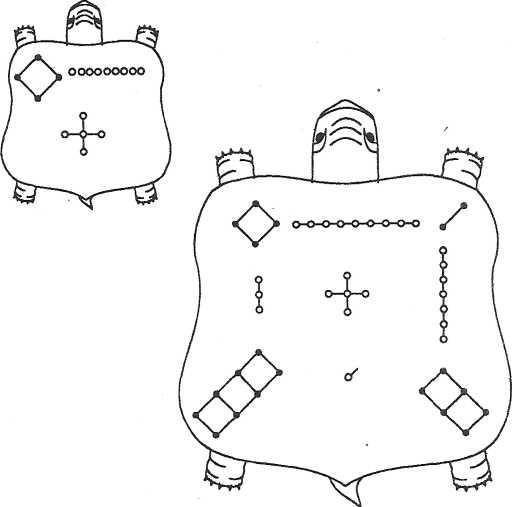
Подсчитав количество кружков в каждой из фигур, мы получим наш прежний магический квадрат. А существуют ли другие магические квадраты?

Сначала выясним, чему может равняться сумма чисел в строке. Так как 1 + 2+3+4 + 5+6 + 7 + 8+9 = 45, то в каждой строке (столбце, диагонали) стоит треть от этого числа, т.е. 15.

Теперь определим число, стоящее в центре. Обозначим его через х и сложим все числа, стоящие на вертикали, горизонтали и диагоналях, проходящих через центр. При этом каждое число войдет в сумму по одному разу, а центральное — четыре раза, поэтому 4*15=(45 - х)+4х. Отсюда находим, что х = 5.

Из соображений четности следует, что в углах квадрата должны стоять четные числа, а в серединах сторон - нечетные.

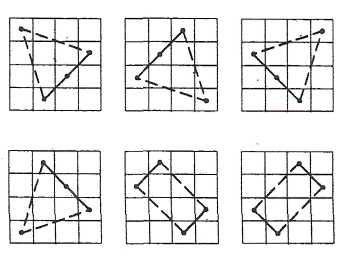
Теперь уже нетрудно убедиться, что все магические квадраты получаются из квадрата   “ло-шу” с помощью поворотов вокруг центра и симметрии относительно средних линий и диагоналей. Всего же их 8.

По образу квадрата “ло-шу” в дальнейшем стали придумывать магические квадраты большего размера. Первым квадратом, придуманным европейцем, считается квадрат Альбрехта Дюрера, изображенный на его знаменитой гравюре Меланхолия . Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки.

16	2	3	13
5	11	10	8
9	7	6	12
4	14	15	1

Магическим квадратом стали называть квадрат nхn, в клетках которого записаны числа от 1 до п² так, что в каждой строке, каждом столбце и по каждой из двух его диагоналей сумма чисел одна и та же. Найти эту сумму не составляет труда, так как 1+2+…+n2=n²(n²+1)/2. Поэтому сумма в каждой строке (столбце, диагонали) равна n(n²+1)/2.

Долгое время составление магических квадратов было весьма популярным занятием математиков и любителей математики. Выдающийся американский общественный деятель, дипломат и ученый Бенджамин Франклин в молодости забавлялся составлением причудливых магических квадратов, скрашивая скучные часы на службе в Законодательном Собрании штата Пенсильвания. Его квадрат 8X8, изображенный на рисунке 4, обладает многими дополнительными свойствами.

52	61	4	13	20	29	36	45
14	3	62	51	46	35	30	19
63	60	5	12	21	28	37	44
11	6	59	54	43	38	27	22
55	58	7	10	23	26	39	42
9	8	57	56	41	40	25	24
50	63	2	15	18	31	34	47
16	1	64	49	48	33	32	17

Рис. 4

Сумма чисел в каждой строке здесь равна 8(64+1)/2=260. При этом сумма чисел в каждой половине строки и в каждой половине столбца равна 130. Четыре числа в углах вместе с четырьмя числами в центре вновь дают 260. И еще много подобных соотношений можно отыскать в этом квадрате.

1	12	6	15
8	13	3	10
11	2	16	5
14	7	9	4

Известны и небольшие квадраты с дополнительными свойствами. Так, квадрат 4X4, изображенный на рисунке слева, имеет сумму 34 не только по строкам, столбцам и диагоналям, но и по “разломанным диагоналям” (рисунок справа ), а также в каждом квадрате 2X2. Если такими квадратами замостить плоскость, то каждый квадрат 4X4 в этой плоскости будет магическим.

Создавались магические квадраты больших размеров. Известный немецкий математик М. Штифель в книге “Arithmetica integra”, вышедшей в 1544 году, приводит магический квадрат размерами 16X16. Известны магические квадраты размерами 43 X 43. Изготовление большого магического квадрата не составляет труда, поскольку имеются алгоритмы, позволяющие строить магические квадраты любых размеров.

Следует, правда, отметить, что магического квадрата 2X2 не существует.

При всем том, многое о магических квадратах неизвестно. Неизвестно, как зависит количество магических квадратов nхn от значения размера n. Известно лишь, что квадратов 4X4 существует 880, а квадратов 5X5 — около четверти миллиона. Прямой перебор всех возможностей даже для квадратов 5 X 5 огромен.

В табличном процессоре Excel показать пример арифметической и геометрической прогрессий, а также построение графика этой последовательности:

номер члена арифметической прогрессии	значение члена арифметической прогрессии	номер члена арифметической прогрессии	значение члена арифметической прогрессии
1	3	1	3
2	=B2+5	2	8
3	=B3+5	3	13
4	=B4+5	4	18
5	=B5+5	5	23
6	=B6+5	6	28
7	=B7+5	7	33
8	=B8+5	8	38
9	=B9+5	9	43
10	=B10+5	10	48
11	=B11+5	11	53
12	=B12+5	12	58

номер члена геометрической прогрессии	значение члена геометрической прогрессии	номер члена геометрической прогрессии	значение члена геометрической прогрессии
1	3	1	3
2	=B2*2	2	6
3	=B3*2	3	12
4	=B4*2	4	24
5	=B5*2	5	48
6	=B6*2	6	96
7	=B7*2	7	192
8	=B8*2	8	384
9	=B9*2	9	768
10	=B10*2	10	1536
11	=B11*2	11	3072
12	=B12*2	12	6144

В рубрике “Это интересно” начало истории “Выгодная сделка”

Выгодная сделка.

Когда и где происходила эта история – неизвестно. Возможно, что и вовсе не происходила; даже скорее всего, что так. Но быль это или небылица, история достаточно занятна, чтоб её послушать.

Богач – миллионер возвратился из отлучки необычайно радостный: у него была в дороге счастливая встреча сулившая большие выгоды.

“Бывают же такие удачи: - рассказывал он домашним. – Неспроста, видимо, говорят, что деньга на деньгу набегает. Вот и на мою деньгу денежка бежит. И как неожиданно. Повстречался мне в пути незнакомец, из себя не видный. Мне б и разговаривать с ним не пристало, да он сам начал, как проведал, что у меня достаток есть. И такое к концу разговора предложил выгодное дельце, что у меня дух захватило.

- Сделаем, - говорит,- с тобой такой уговор. Я буду целый месяц приносить тебе по сотне тысяч рублей. Не даром, разумеется, но плата пустячная. В первый день я должен по уговору заплатить – смешно вымолвить – всего только одну копейку. Я ушам не поверил:

- Одну копейку? – переспрашиваю.

- Одну копейку, - говорит.- За вторую сотню тысяч заплатишь две копейки.

-Ну, - не терпится мне. – А дальше?

- А дальше: за третью сотню тысяч 4 копейки, за четвёртую 8, за пятую – 16. И так целый месяц, каждый день вдвое больше против предыдущего.

- И потом что? – спрашиваю.

- Всё, - говорит, - больше ничего не потребую. Только крепко держать уговор: каждое утро буду носить по сотне тысяч рублей, а ты плати, что сговорено. Раньше месяца кончать не смей.

Сотни тысяч рублей за копейки отдаёт! Если деньги не фальшивые, то не в полном уме человек. Однако же дело выгодное, упускать не надо.

-Ладно, - говорю. – Неси деньги. Я-то свои уплачу аккуратно. Сам, смотри, не обмани: правильные деньги приноси.

- Будь спокоен, - говорит, - завтра с утра жди.

Одного только боюсь: придёт ли? Как бы не спохватился, что слишком невыгодное дело затеял! Ну, до завтра не долго ждать”.

Пошёл день. Рано утром постучал богачу в окошко тот самый незнакомец, которого он встретил в дороге.

- Деньги готовь, - говорит. – Я свои принёс.

И, действительно, войдя в комнату, странный человек стал выкладывать деньги – настоящие, не фальшивые. Отсчитал ровно сто тысяч и говорит:

- Вот моё по уговору. Твой черёд платить.

Богач положил на стол медную копейку и с опаской дожидался, возьмёт гость монету или раздумает, деньги свои назад потребует. Посетитель осмотрел копейку, взвесил в руке и спрятал в суму.

- Завтра в такое же время жди. Дане забудь, две копейки припаси, - сказал он и ушёл.

Богач не верил удаче: сто тысяч с неба свалилось! Снова пересчитал деньги, удостоверился хорошенько, что не фальшивые: всё правильно. Запрятал деньги подальше и стал ждать завтрашней уплаты.

Ночью взяло его сомнение: не разбойник ли простаком прикинулся, хочет поглядеть, куда деньги прячу, да и нагрянуть с шайкой лихих людей?

Запер богач двери покрепче, с вечера в окно поглядывал, прислушивался, долго заснуть не мог. На утро снова стук в окно: незнакомец деньги принёс. Отсчитал сто тысяч, получил свои две копейки, спрятал монету в суму и ушёл, бросив на прощанье:

-К завтрашнему четыре копейки, смотри, приготовь. Снова радуется богач: вторая сотня тысяч даром досталась. А гость на грабителя не похож: по сторонам не глядит, не высматривает, свои только копейки требует. Чудак! Побольше бы таких на свете, умным людям хорошо бы жилось…

Явился незнакомец и на третий день – третья сотня тысяч перешла богаче за 4 копейки.

Ещё день, и таким же манером явилась четвёртая сотня тысяч – за 8 копеек.

Пришла и пятая сотня тысяч – за 16 копеек. Потом шестая за 32 копейки.

Спустя семь дней от начала сделки получил наш богач уже семьсот тысяч рублей, а уплатил пустяки:

1 коп.+2 коп.+4 коп.+8 коп.+16 коп.+32 коп.+64 коп.=1р.27коп

Понравилось это алчному миллионеру, и он уже стал сожалеть, что договорился всего на один месяц. Больше трёх миллионов получить не удастся. Склонить разве чудака продлить срок ещё хоть на полмесяца? Боязно: как бы не сообразил, что зря деньги отдаёт…

А вы, ребята, как думаете – кто приходил каждое утро к богачу: простак, разбойник или кто – то другой?

Урок 6 “Арифметическая и геометрическая прогрессии”.

В рубрике “Это интересно” продолжение истории “Выгодная сделка”. Для учеников вывешивается таблица, в которую они вносят полученные ими результаты:

	Ежедневная плата богача
За 1 сотню тысяч рублей
За 2 сотню тысяч рублей
За 3 сотню тысяч рублей
За 4 сотню тысяч рублей
За 5 сотню тысяч рублей
За 6 сотню тысяч рублей
За 7 сотню тысяч рублей
За 8 сотню тысяч рублей
За 9 сотню тысяч рублей
За 10 сотню тысяч рублей
За 11 сотню тысяч рублей
За 12 сотню тысяч рублей
За 13 сотню тысяч рублей
За 14 сотню тысяч рублей
За 15 сотню тысяч рублей
За 16 сотню тысяч рублей
За 17 сотню тысяч рублей
За 18 сотню тысяч рублей
За 19 сотню тысяч рублей
За 20 сотню тысяч рублей
За 21 сотню тысяч рублей
За 22 сотню тысяч рублей
За 23 сотню тысяч рублей
За 24 сотню тысяч рублей
За 25 сотню тысяч рублей
За 26 сотню тысяч рублей
За 27 сотню тысяч рублей
За 28 сотню тысяч рублей
За 29 сотню тысяч рублей
За 30 сотню тысяч рублей
всего

	Ежедневная плата богача
За 1 сотню тысяч рублей	1 коп
За 2 сотню тысяч рублей	2 коп
За 3 сотню тысяч рублей	4 коп
За 4 сотню тысяч рублей	8 коп
За 5 сотню тысяч рублей	16 коп
За 6 сотню тысяч рублей	32 коп
За 7 сотню тысяч рублей	64коп
За 8 сотню тысяч рублей	1р 28 коп
За 9 сотню тысяч рублей	2р 56 коп
За 10 сотню тысяч рублей	5р 12 коп
За 11 сотню тысяч рублей	10р 24 коп
За 12 сотню тысяч рублей	20р 48 коп
За 13 сотню тысяч рублей	40р 96 коп
За 14 сотню тысяч рублей	81р 92 коп
За 15 сотню тысяч рублей	163р 84 коп
За 16 сотню тысяч рублей	327р 68 коп
За 17 сотню тысяч рублей	655р 36 коп
За 18 сотню тысяч рублей	1 310р 72 коп
За 19 сотню тысяч рублей	2 621р 44 коп
За 20 сотню тысяч рублей	5 242р 88 коп
За 21 сотню тысяч рублей	10 485р 76 коп
За 22 сотню тысяч рублей	20 971р 52 коп
За 23 сотню тысяч рублей	41 943р 04 коп
За 24 сотню тысяч рублей	83 886р 08коп
За 25 сотню тысяч рублей	167 772р 16 коп
За 26 сотню тысяч рублей	335 544р 32 коп
За 27 сотню тысяч рублей	671 088р 64 коп
За 28 сотню тысяч рублей	1 342 177р 28 коп
За 29 сотню тысяч рублей	2 684 354р 56 коп
За 30 сотню тысяч рублей	5 368 709р 12 коп
всего

Вычисление также провести в электронной таблице Excel, показав работу с форматом ячеек на примере денежного формата.

Урок 7 “Арифметическая и геометрическая прогрессии”.

В рубрике “Это интересно” показать ученикам рациональный способ подсчёта суммы, выплаченной миллионером в истории “Выгодная сделка”. Этот способ можно применить для вычисления любой подобной суммы.

Когда гость ушёл в последний раз, миллионер подсчитал, во что обошлись ему столь дешёвые на первый взгляд три миллиона рублей. Оказалось, что уплачено было незнакомцу

10 737 418 р. 23 коп.

Без малого 11 миллионов!.. А ведь началось с одной копейки. Незнакомец мог бы приносить по три сотни тысяч и всё-таки не прогадал бы.

Прежде чем кончить с этой историей, посмотрите, каким способом можно ускорить подсчёт убытков миллионера; другими словами – как скорее всего выполнить сложение ряда чисел:

1+2+4+8+16+32+64+ и т.д.

Нетрудно подметить следующую особенность этих чисел:

1=1

2=1+1

4=(1+2)+1

8=(1+2+4)+1

16=(1+2+4+8)+1

32=(1+2+4+8+16)+1 и т.д.

Видно, что каждое число этого ряда равно всем предыдущим, вместе взятым, плюс одна единица. Поэтому когда нужно сложить все числа такого ряда, например, от 1 до 32 768, то мы прибавляем лишь к последнему числу (32 768) сумму всех предыдущих, иначе сказать – прибавляем то же последнее число без единицы (32 768 – 1). Получаем 65 535

Этим способом можно подсчитать убытки алчного миллионера очень быстро, как только узнаем, сколько уплатил он в последний раз. Его последний платёж был 5 368 709р 12 коп.

Поэтому, сложив 5 368 709р 12 коп. +5 368 709р 11 коп., получаем сразу искомый результат 10 737 418р 23 коп.

Урок 8. “Сумма n первых членов арифметической прогрессии и геометрической прогрессии”

При объяснении нового материала – доказательства теоремы о сумме первых n членов арифметической прогрессии - удобно провести исторический пример.

В Германии, в конце 18 в., для того чтобы заставить учеников поработать, учитель дал им задание подсчитать сумму всех натуральных чисел от 1 до 100. Какова же было его удивление, когда уже через несколько минут один ученик сказал ему ответ: искомая сумма равна 5050! Этот ученик, Карл Фридрих Гаусс, а ему было тогда 10 лет, стал одним из великих математиков мира. Как же маленькому Гауссу удалось быстро подсчитать сумму?

Решение

Рассмотреть нахождение суммы первых 100 натуральных чисел методом Гаусса:

1 + 2 + 3 + 4 + … + 96 + 97 + 98 + 99 + 100 = (1+100) + (2 + 99) +… + (48+53) +(49 + 52) +(50 +51) =50*101 = 5050

При доказательстве теоремы о сумме первых n членов геометрической прогрессии рассмотреть старинную русскую задачу о продаже лошади из учебника Л.Ф.Магницкого “Арифметика”

Проторговался ли купец?

Некто продавал коня и просил за него 1000 рублей. Купец сказал, что за коня запрошена слишком большая цена. "Хорошо, - ответил продавец, - если ты говоришь, что конь дорого стоит, то возьми его себе даром, а заплати только за его гвозди в подковах. А гвоздей во всякой подкове по 6 штук. И будешь ты мне за них платить таким образом: за первый гвоздь полушку, за второй гвоздь заплатишь две полушки, за третий гвоздь - четыре полушки, и так далее за все гвозди: за каждый в два раза больше, чем за предыдущий". Купец же, думая, что заплатит намного меньше, чем 1000 рублей, согласился. Проторговался ли купец, и если да, то насколько?

Решение задачи

За 24 подковных гвоздя пришлось уплатить

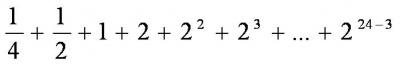
копеек. Сумма эта равна

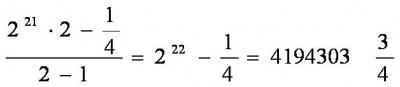
копеек, т.е. около 42 тысяч рублей. При таких условиях не обидно дать и лошадь в придачу

На данном уроке продемонстрировать ученикам нахождения суммы n первых членов арифметической и геометрической прогрессий с помощью функции суммы табличного процессора.

1	2	3	4	5	6	7	8	9	10	=СУММ(A1:J1)
1	2	3	4	5	6	7	8	9	10	55

В рубрике “Это интересно” разместить биографию Карла Фридриха Гаусса.

Карл Фридрих Гаусс (1777-1855) — немецкий математик, астроном, геодезист и физик, иностранный член-корреспондент (1802) и иностранный почетный член (1824) Петербургской Академии Наук

Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры (доказательство основной теоремы алгебры), теории чисел (квадратичные вычеты), дифференциальной геометрии (внутренняя геометрия поверхностей), математической физики (принцип Гаусса), теории электричества и магнетизма, геодезии (разработка метода наименьших квадратов) и многих разделов астрономии.

Карл Гаусс родился 30 апреля 1777, Брауншвейг, ныне Германия. Скончался 23 февраля 1855, Геттинген, Ганноверское королевство, ныне Германия,

Юный гений

Еще при жизни Гаусс был удостоен почетного титула «принц математиков». Он был единственным сыном бедных родителей. Школьные учителя были так поражены его математическими и лингвистическими способностями, что обратились к герцогу Брауншвейгскому с просьбой о поддержке, и герцог дал деньги на продолжение обучения в школе и в Геттингенском университете (в 1795-98). Степень доктора Гаусс получил в 1799 в университете Хельмштедта.

«Арифметические исследования»

Первое же обширное сочинение Гаусса «Арифметические исследования» (опубликовано в 1801) на многие годы определило последующее развитие двух важных разделов математики — теории чисел и высшей алгебры. Множество важных и тонких результатов приведены в «Арифметических исследованиях». В конце сочинения Гаусс приводит полную теорию уравнений деления круга и, указывая их связь с задачей построения правильных многоугольников, решает стоявшую с античных времен проблему о возможности построения циркулем и линейкой правильного многоугольника с заданным числом сторон. Гаусс указал все числа, при которых построение правильного многоугольника с помощью циркуля и линейки возможно. Это пять так называемых гауссовых простых чисел: 3, 5, 17, 257 и 65337, а также умноженные на любую степень двойки произведения различных (не повторяющихся) гауссовых чисел. Например, построить с помощью циркуля и линейки правильный (3х5х17)-угольник можно, а правильный 7-угольник нельзя, так как семерка не гауссово простое число.

Разумеется, доказанный Гауссом результат — пример так называемой чистой теоремы существования; утверждается, что построить с помощью циркуля и линейки правильный многоугольник с «допустимым» числом сторон можно, но ничего не говорится о том, как это сделать. Карл Гаусс предложил также явный способ построения с помощью циркуля и линейки правильного 17-угольника. Это событие Гаусс посчитал столь значительным, что отметил его в «Дневнике» (запись от 30 марта 1796 ) и завещал высечь правильный 17-угольник на своем надгробии (воля Гаусса была исполнена).

Основная теорема алгебры

С именем Гаусса также связана основная теорема алгебры, согласно которой число корней многочлена (действительных и комплексных) равно степени многочлена (при подсчете числа корней кратный корень учитывается столько раз, какова его степень). Первое доказательство основной теоремы алгебры Гаусс дал в 1799, а позднее предложил еще несколько доказательств.

Математика и астрономия

Гаусс живо интересовался не только «чистой математикой», но и ее приложениями. В области прикладной математики он не только получил ряд важных результатов, но и создал новые направления в науке.

Занимая с 1807 кафедру математики и астрономии Геттингенского университета и возглавляя астрономическую обсерваторию того же университета, Карл Гаусс на протяжении более двух десятилетий занимается изучением орбит малых планет и их возмущений. Мировую известность обрел разработанный Гауссом метод определения эллиптической орбиты по трем наблюдениям. Применение этого метода к малой планете Церера позволило вновь найти ее на небе после того, как она была утеряна вскоре после ее открытия астрономом Дж. Пиацци (1801). Не меньший успех сопутствовал применению метода Гаусса к другой малой планете, Палладе (1802).

В 1809 выходит фундаментальный труд Гаусса «Теория движения небесных тел», в котором изложены методы вычисления планетных орбит, используемые (с незначительными усовершенствованиями) и поныне.

В 1812 Карл Гаусс познакомил математический мир со своей гипергеометрической функцией, частным случаем которой являются многие из так называемых специальных функций математической физики. В той же работе он рассматривает и вопросы сходимости бесконечных рядов, важные для астрономических вычислений.

Высшая геодезия. Неевклидова геометрия

В 1818 Карл Гаусс одним из первых начинает размышлять над созданием неевклидовой геометрии, но от публикации полученных результатов воздерживается, опасаясь, по собственному признанию, «криков беотийцев» (т.е. возражений и насмешек невежд).

Десятилетие 1820-30 застает Гаусса за проведением геодезической съемки Ганноверского королевства и составлением его подробной карты. Гаусс не только проделывает огромную организационную работу и руководит измерением длины дуги меридиана от Геттингена до Альтоны, но и создает основы «высшей геодезии», занимающейся описанием действительной формы земной поверхности. Обобщающий труд «Исследования о предметах высшей геодезии» Гаусс создает в 1842-47. В основе этого фундаментального труда лежат также принадлежащие Гауссу идеи так называемой внутренней геометрии поверхности, изложенной им в сочинении «Общие исследования о кривых поверхностях» (1827). Локальные (т. е. характеризующие малую окрестность точки) свойства поверхности, по мысли Гаусса, естественнее связывать не с «посторонними», введенными извне, а с внутренними криволинейными координатами и выражать через дифференциальную форму от внутренних координат. Если поверхность изгибать не растягивая, то ее внутренние свойства остаются неизменными. Впоследствии по образу и подобию внутренней геометрии поверхностей Гаусса была создана многомерная риманова геометрия.

Открытия в области физики

В 1830-40 гг. Гаусс много внимания уделяет проблемам физики. В 1832 он создает так называемую абсолютную систему единиц, приняв за основные три единицы; единицу времени 1 с, единицу длины 1 мм и единицу массы 1 г. В 1833 в тесном сотрудничестве с Вильгельмом Вебером Гаусс строит первый в Германии электромагнитный телеграф. В 1839 выходит сочинение Гаусса «Общая теория сил притяжения и отталкивания, действующих обратно пропорционально квадрату расстояния», в которой излагает основные положения теории потенциала и доказывает знаменитую теорему Гаусса—Остроградского. Работа «Диоптрические исследования» (1840) Гаусса посвящена теории построения изображений в сложных оптических системах.

Значение исследований Гаусса

Многие исследования Карл Гаусс не публиковал при жизни. Они сохранились в виде очерков, набросков, переписки с друзьями. Изучением этих трудов до Второй мировой войны занималось Геттингенское научное общество, которому удалось издать 12 томов сочинений Гаусса. Наиболее интересную часть наследия составляет уже упоминавшийся дневник.

Научное творчество Карла Гаусса наглядно показывает неосновательность деления наук на «чистые» и «прикладные»: «принц математиков» находил практические применения результатам своих фундаментальных исследований и из конкретных задач прикладных областей умел извлекать проблемы, представляющие интерес для фундаментальной науки.

Урок 9. “Сумма n первых членов арифметической прогрессии и геометрической прогрессии”.

На этом уроке при решении задач на нахождение суммы арифметической и геометрической прогрессий можно предложить учащимся задачи из истории разных стран, показав тем самым, что все народы в разные времена интересовались этой темой.

О том, как давно была известна геометрическая прогрессия, свидетельствуют папирусы Ахмеса. Некоторые задачи имеют отвлеченный характер. Например:

 “В доме было 7 кошек.

Каждая кошка съедает 7 мышей.

Каждая мышь съедает 7 колосьев.

Каждый колос дает 7 растений.

На каждом растении вырастает 7 мер зерна.

Сколько всех вместе?”.

Автора задачи не интересует, о каких вещах идет речь, важно только их общее количество.

И на Руси решались похожие задачи. Еще в XIX веке в деревнях загадывали:

“Шли 7 старцев.

У каждого старца по 7 костылей.

На каждом костыле по 7 сучков.

На каждом сучке по 7 кошелей.

В каждом кошеле по 7 пирогов.

В каждом кошеле по 7 воробьев.

Сколько всего?”

А ведь это та же задача Ахмеса. Прожившая тысячелетия она сохранилась почти неизменной.

Древнейшая русская задача о делении хлеба.

Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвёртый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трёх остальных. Сколько нужно дать каждому?

Решение:

у- разность арифметической прогрессии

На основании условий задачи составим следующие два уравнения:

х + (х + у) + (х + 2у) + (х + 3у) + (х + 4у) = 100

7(х + (х + у)) = (х+2у) + (х+3у) + (х+4у)

На данном уроке ученикам можно самостоятельно найти сумму прогрессии, пользуясь функцией суммы табличного процессора Excel.

Уроки 10 – 11. “Решение задач”.

На данном уроке решаются задачи практического характера. Геометрическая прогрессия имеет очень широкие приложения в экономике. С ее помощью банк производит расчеты с вкладчиком, решает, стоит ли вкладывать деньги в крупные проекты, доход от которых будет получен через несколько лет и т. д. В задачах рассмотрена методика расчетов за банковский кредит. Как иногда бывает, условия кредита таковы, что заемщику предстоит выплатить дополнительную сумму денег, которая превышает на много весь кредит. Поэтому эти знания экономики, которые получат учащиеся посредством решения экономических задач на уроках математики, взятых из жизни застрахуют от ошибок. Может в будущей взрослой жизни ребята предотвратят ошибок, заставят задумываться, в том «какой кредит выгоднее?» Так же можно рассмотреть задачи экономического содержания, взятые из литературных источников. Таким образом, осуществляется межпредметная связь не только с экономикой, но и с литературой.

Задача.

При одном из видов кредитования заем в 6 000руб. погашается в течение года по 500руб. ежемесячно, вносимых в последний день месяца одновременно с уплатой 5% в месяц от долга. Найти размер всей платы за кредит.

Задача.

В романе М .Е.Салтыкова-Щедрина «Господа Головлевы» сын Порфирия Владимировича Петя проиграл в карты казенные 3000 руб. и попросил у бабушки эту сумму взаймы. Он говорил: «Я бы хороший процент дал. Пять процентов в месяц». Подсчитайте, сколько денег готов был вернуть Петя через год, согласись бабушка на его условия?

Задача.

В новелле О.Бальзака « Гобсек » один из героев, господин Дервиль, взял у ростовщика Гобсека сумму в 150000 франков сроком на 10 лет по 15% годовых. Вычислите, какую сумму он вернул по прошествии этого срока?

Задача.

Предположим, что в начале нашей эры в банк положили 1 копейку, ежегодно начисляли 5% годовых. В какую сумму превратится эта копейка через 2000 лет, т.е. к нашему времени?

Задача.

Предположим, что в 1776 году, когда образовались США, 1 доллар был отдан под 10 % годовых. В какую сумму он превратился к 2076 году – 300-летней годовщине образования США?

На данных уроках нужно показать ученикам, как можно вычислить плату по кредиту, в котором процент начисляется от оставшейся суммы, если известна налоговая ставка. Показать, как создать электронную таблицу, в которой происходит автоматический пересчёт данных при смене любых из условий (суммы, взятой в кредит, срока или процентной ставки). Таким образом, ученики в самостоятельной жизни легко смогут сделать примерные расчёты того, на какую сумму они могут рассчитывать, на какой срок им удобнее взять кредит и т.д.

Например,

Сумма, взятая в кредит и остаток долга	Срок кредитования (годы)	Процентная ставка (в%)	Сумма, выплаченная банку в текущем месяце в счёт погашения долга	Сумма, выплаченная банку в текущем месяце в счёт процентов
100000	3	29	=$A$2/(12*$B$2)	=A2*$C$2/(100*12)
=A2-D2			=$A$2/(12*$B$2)	=A3*$C$2/(100*12)
=A3-D3			=$A$2/(12*$B$2)	=A4*$C$2/(100*12)
=A4-D4			=$A$2/(12*$B$2)	=A5*$C$2/(100*12)
=A5-D5			=$A$2/(12*$B$2)	=A6*$C$2/(100*12)
=A6-D6			=$A$2/(12*$B$2)	=A7*$C$2/(100*12)
=A7-D7			=$A$2/(12*$B$2)	=A8*$C$2/(100*12)
=A8-D8			=$A$2/(12*$B$2)	=A9*$C$2/(100*12)
=A9-D9			=$A$2/(12*$B$2)	=A10*$C$2/(100*12)
=A10-D10			=$A$2/(12*$B$2)	=A11*$C$2/(100*12)
=A11-D11			=$A$2/(12*$B$2)	=A12*$C$2/(100*12)
=A12-D12			=$A$2/(12*$B$2)	=A13*$C$2/(100*12)
=A13-D13			=$A$2/(12*$B$2)	=A14*$C$2/(100*12)
=A14-D14			=$A$2/(12*$B$2)	=A15*$C$2/(100*12)
=A15-D15			=$A$2/(12*$B$2)	=A16*$C$2/(100*12)
=A16-D16			=$A$2/(12*$B$2)	=A17*$C$2/(100*12)
=A17-D17			=$A$2/(12*$B$2)	=A18*$C$2/(100*12)

Сумма, взятая в кредит и остаток долга	Срок кредитования (годы)	Процентная ставка (в%)	Сумма, выплаченная банку в текущем месяце в счёт погашения долга	Сумма, выплаченная банку в текущем месяце в счёт процентов
100 000,00р.	3	29	2 777,78р.	2 416,67р.
97 222,22р.			2 777,78р.	2 349,54р.
94 444,44р.			2 777,78р.	2 282,41р.
91 666,67р.			2 777,78р.	2 215,28р.
88 888,89р.			2 777,78р.	2 148,15р.
86 111,11р.			2 777,78р.	2 081,02р.
83 333,33р.			2 777,78р.	2 013,89р.
80 555,56р.			2 777,78р.	1 946,76р.
77 777,78р.			2 777,78р.	1 879,63р.
75 000,00р.			2 777,78р.	1 812,50р.
72 222,22р.			2 777,78р.	1 745,37р.
69 444,44р.			2 777,78р.	1 678,24р.
66 666,67р.			2 777,78р.	1 611,11р.
63 888,89р.			2 777,78р.	1 543,98р.
61 111,11р.			2 777,78р.	1 476,85р.
58 333,33р.			2 777,78р.	1 409,72р.
55 555,56р.			2 777,78р.	1 342,59р.

Уроки 12-13 “Бесконечно убывающая геометрическая прогрессия”.

На этих уроках в домашнем задании учеников есть творческое задание – придумать задачи на арифметическую прогрессию, геометрическую прогрессию, бесконечно убывающую геометрическую прогрессию. На следующем уроке разобрать наиболее интересные из придуманных, также задать задачу ученикам в качестве домашнего задания, которое нужно будет сдать на проверку автору.

Представить графическую интерпретацию бесконечно убывающей геометрической прогрессии. Например, прогрессия первый член которой равен 3, а знаменатель равен 0,5.

Урок 14. “Решение задач”

В рубрике “Это интересно” разместить легенду о шахматной доске

Легенда о шахматной доске.

Шахматы – одна из самых древних игр. Она существует уже многие века, и неудивительно, что с нею связаны различные предания, правдивость которых за давностью времени, невозможно проверить.

Вот одна из подобных легенд. Чтоб понять её достаточно знать, что игра происходит на доске, разграфлённой на 64 клетки (попеременно чёрные и белые).

I

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищён её остроумием и разнообразием возможных в ней положений.

Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.

Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый учёный, получавший средства к жизни от своих учеников.

- Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, - сказал царь.

Мудрец поклонился.

- Я достаточно богат, чтобы исполнить самое смелое твоё пожелание, - продолжал царь. – Назови награду, которая тебя удовлетворит, и ты получишь её.

Сета молча.

- Не робей, - одобрил его царь. – Выскажи своё желание. Я не пожалею ничего, чтоб исполнить его.

- Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.

Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.

-Повелитель, - сказал Сета, - прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.

- Простое пшеничное зерно? – изумился царь.

-Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью 4, за четвёртую - 8, за пятую – 16, за шестую – 32…

- Довольно, - с раздражением прервал его царь. – Ты получишь свои зёрна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай. Слуги мои вынесут тебе мой мешок с пшеницей.

Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца.

II

За обедом царь вспомнил об изобретении шахмат и послал узнать, унёс ли уже безрассудный Сета свою жалкую награду.

- Повелитель, - был ответ, - приказание твоё исполняется. Придворные математики исчисляют число следуемых зёрен.

Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медленно.

Вечером, отходя ко сну, царь ещё раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.

- Повелитель, - ответили ему, - математики твои трудятся без устали и надеются ещё до рассвета закончить подсчёт.

- Почему медлят с этим делом? – гневно воскликнул царь. – Завтра, прежде чем я проснусь, всё до последнего зерна должно бать выдано Сете. Я дважды не приказываю.

Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.

- Прежде чем скажешь о твоём деле, - объявил Шерам, - я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.

- Ради этого я и осмелился явиться перед тобой в столь ранний час, - ответил старшина. – Мы добросовестно исчислили всё количество зёрен, которое желает получить Сета. Число это тат велико …

- Как бы велико оно ни было, - надменно перебил его царь, житницы мои не оскуднеют. Награда было обещана и должна быть выдана…

- Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зёрен, какое потребовал Сета. Нет его в житницах целого царства. Не найдётся такого числа зёрен и на всём пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далёкие северные пустыни. Пусть всё пространство их сплошь будет засеяно пшеницей. И всё то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду. С изумлением внимал царь словам старца.

- Назови же мне это чудовищное число, - сказал он в раздумье.

-Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!!!

III

Такова легенда. Действительно ли было то, что здесь рассказано, неизвестно, - но что награда, о которой говорит предание, должна была выразиться именно таким числом, в этом можно убедиться.

Если бы нужно было отсчитать это количество зёрен, отсчитывая по одному зерну в секунду, то в первые сутки было отсчитано 86400 зёрен. Один кубический метр пшеницы (15 миллионов зёрен) был бы отсчитан примерно в полгода. Награда шахматного изобретателя должна была занять объём примерно в 12000000000000 кубических метров, или 12000 кубических километров. При высоте амбара 4метра и ширине 10 метров длина него должна была бы простираться на 300000000километров, что вдвое дальше, чем от Земли до Солнца!

Урок 15. “Обобщающий урок”

Для подготовки к контрольной работе можно составить кодированную домашнюю работу. Задания для класса или групп учеников подобрать таким образом, чтоб полученный ответ в каждом задании нужно было использовать, как известную величину в следующем.

44