Презентация представляет собой иллюстрационные слайды к объяснению материала. 1-ый слайд иллюстрирует введение понятия степени с иррациональным показателем. Далее вводится понятие показательной функции с основанием a и рассматриваются виды графиков, где a > 1 (возрастающая функция) и 0 < a < 1 (убывающая функция). Рассматриваются также свойства показательной функции и примеры применения показательной функции.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Показательная функция, её свойства и график
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Показательная функция, её свойства и график»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2100 руб.
3000 руб.
2020 руб.
2880 руб.
2020 руб.
2880 руб.
2100 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства





 n, то a m a n при a 1 и a m a n при 0 a
n, то a m a n при a 1 и a m a n при 0 a
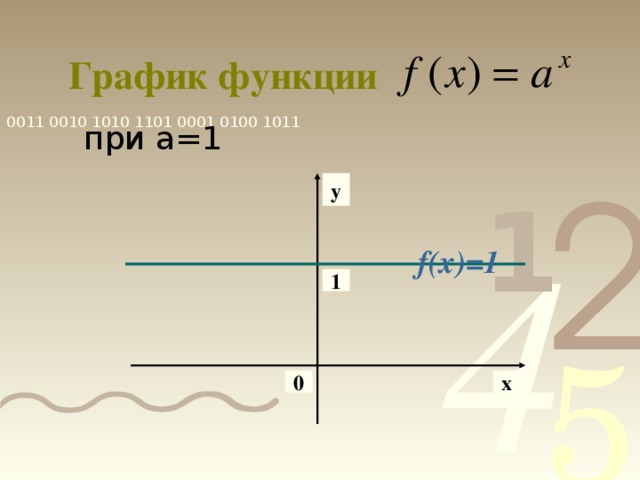
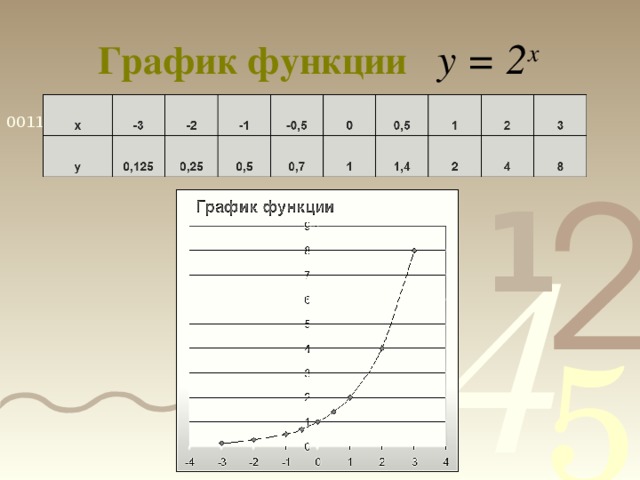
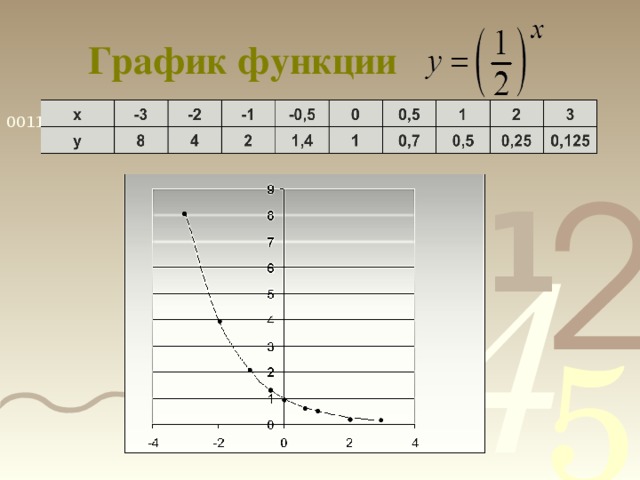
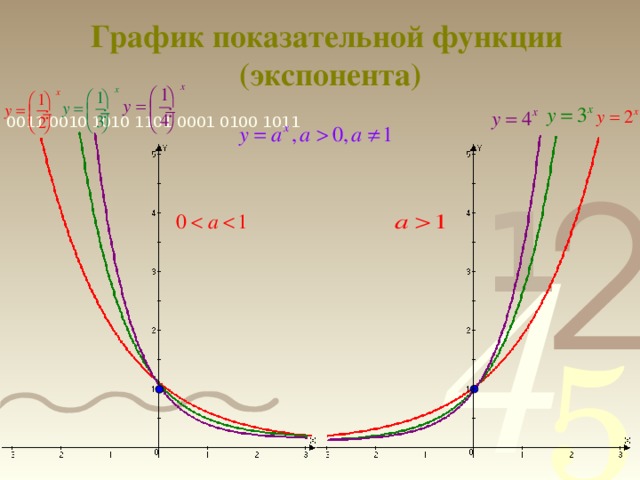

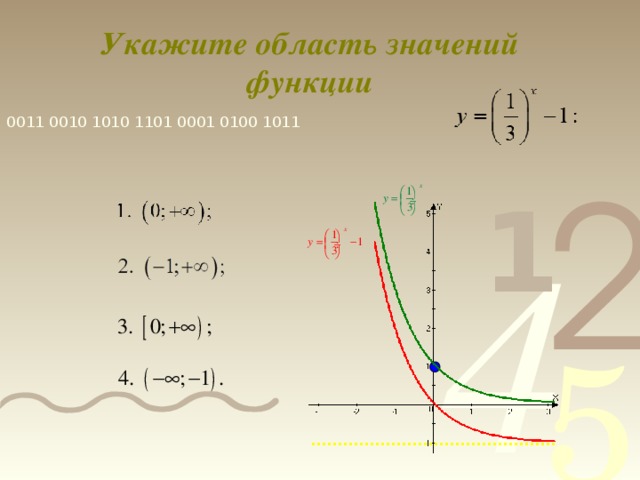
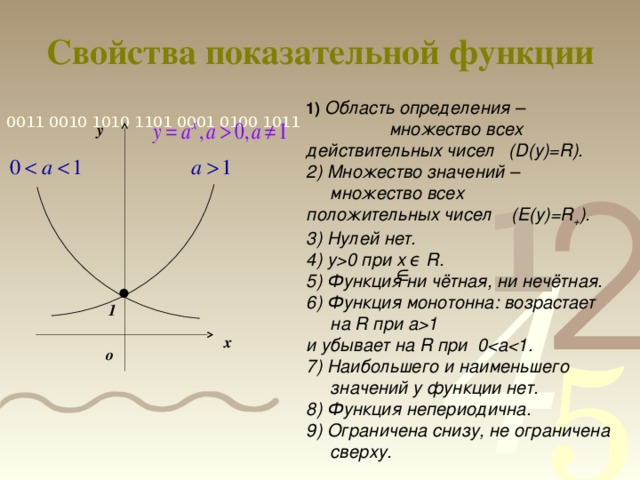 0 при х ϵ R. 5) Функция ни чётная, ни нечётная. 6) Функция монотонна: возрастает на R при а1 и убывает на R при 0 7) Наибольшего и наименьшего значений у функции нет. 8) Функция непериодична. 9) Ограничена снизу, не ограничена сверху. y 1 x о" width="640"
0 при х ϵ R. 5) Функция ни чётная, ни нечётная. 6) Функция монотонна: возрастает на R при а1 и убывает на R при 0 7) Наибольшего и наименьшего значений у функции нет. 8) Функция непериодична. 9) Ограничена снизу, не ограничена сверху. y 1 x о" width="640"