Урок по теме "Решение квадратных неравенств" представлен в виде презентации.Цель-закрепление знаний учащихся о способах решения квадратного неравенства, формирование умений и навыков решения неравенств, развитие логического мышления и математического интереса.Задания разноуровнего характера, содержат теоретичесий материал и практические тестовые вопросы.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Урок по теме "Решение квадратных неравенств"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок по теме "Решение квадратных неравенств" »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2020 руб.
2880 руб.
1630 руб.
2330 руб.
2020 руб.
2880 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
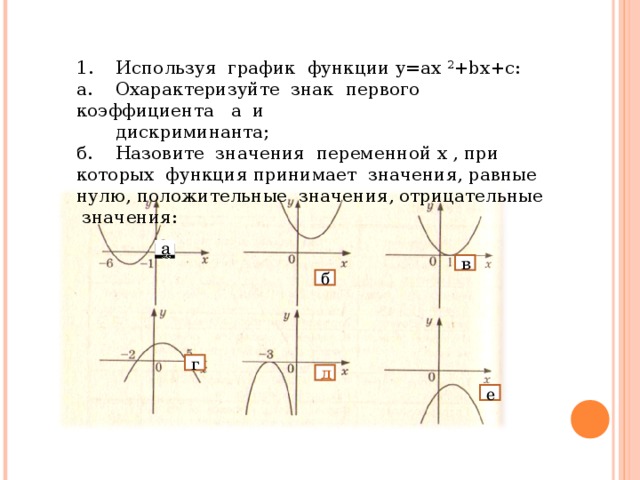

 0, f(x) 0, f(x)≥0 называют квадратными неравенствами или неравенствами второй степени, причем первые два из этих неравенств называют строгими, другие - нестрогими . Перейдем к нахождению решений квадратных неравенств следующих видов: ax 2 +bx+c 0 или ax 2 +bx+c 0. Далее" width="640"
0, f(x) 0, f(x)≥0 называют квадратными неравенствами или неравенствами второй степени, причем первые два из этих неравенств называют строгими, другие - нестрогими . Перейдем к нахождению решений квадратных неравенств следующих видов: ax 2 +bx+c 0 или ax 2 +bx+c 0. Далее" width="640"
 0 , при a 0 являются все действительные числа, а неравенство ax 2 + bx + c , при a 0 не имеет решений; Если D =0 , то решениями неравенства ax 2 + bx + c 0 , являются все действительные значения x , кроме а неравенство ax 2 + bx + c не имеет решений; Если D 0 , то решениями неравенства ax 2 + bx + c 0 при a 0 являются все числа x , лежащие вне отрезка [ x 1 , x 2 ] . А решениями неравенства ax 2 + bx + c являются числа x из интервала ( x 1 , x 2 ) . К содержанию К квадратным неравенствам" width="640"
0 , при a 0 являются все действительные числа, а неравенство ax 2 + bx + c , при a 0 не имеет решений; Если D =0 , то решениями неравенства ax 2 + bx + c 0 , являются все действительные значения x , кроме а неравенство ax 2 + bx + c не имеет решений; Если D 0 , то решениями неравенства ax 2 + bx + c 0 при a 0 являются все числа x , лежащие вне отрезка [ x 1 , x 2 ] . А решениями неравенства ax 2 + bx + c являются числа x из интервала ( x 1 , x 2 ) . К содержанию К квадратным неравенствам" width="640"
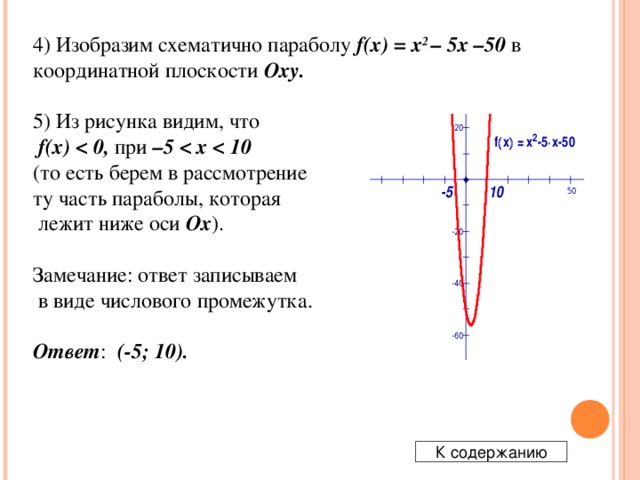
 0 . 3) Найдем нули функции (то есть абсциссы точек пересечения параболы с осью Ox ), для этого решим квадратное уравнение x 2 – 5 x – 50 = 0 . D = 225 = 15 2 , 225 0 , значит уравнение имеет два действительных корня. x 1 = -5; x 2 = 10. Нули функции: x = -5 и x = 10 . Далее" width="640"
0 . 3) Найдем нули функции (то есть абсциссы точек пересечения параболы с осью Ox ), для этого решим квадратное уравнение x 2 – 5 x – 50 = 0 . D = 225 = 15 2 , 225 0 , значит уравнение имеет два действительных корня. x 1 = -5; x 2 = 10. Нули функции: x = -5 и x = 10 . Далее" width="640"


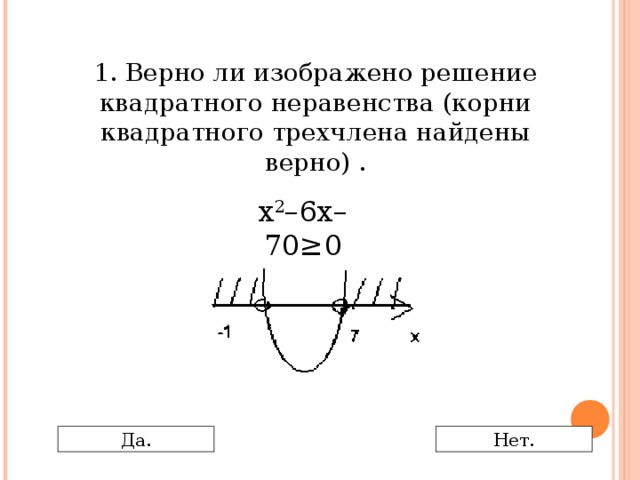
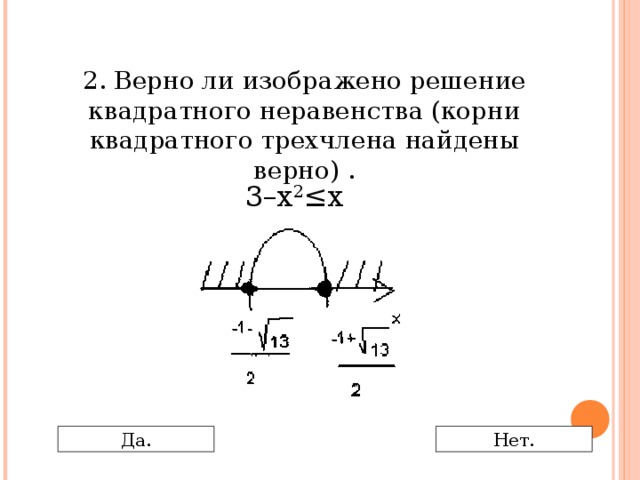
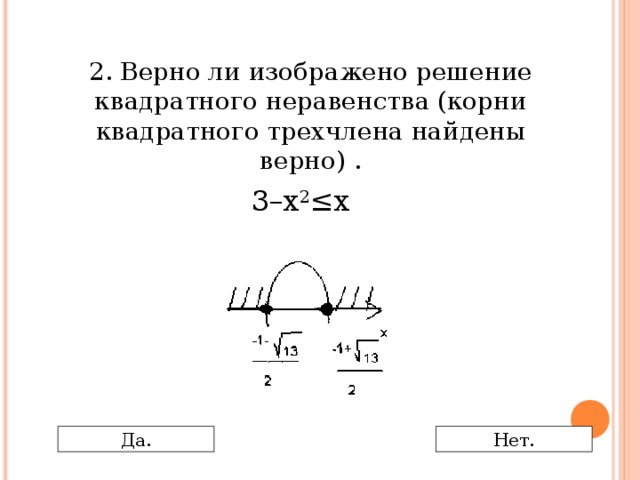
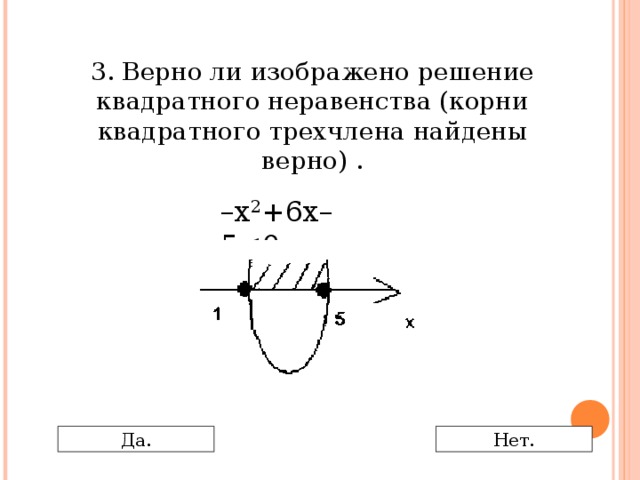
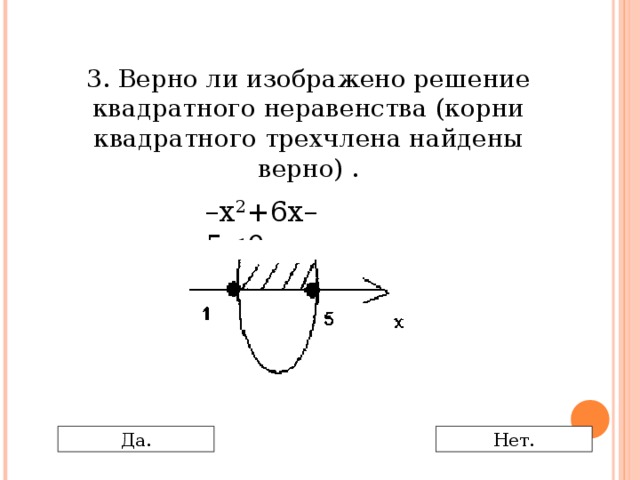
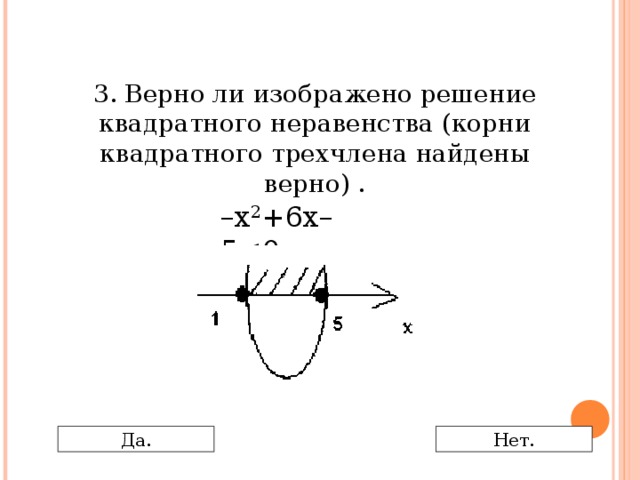
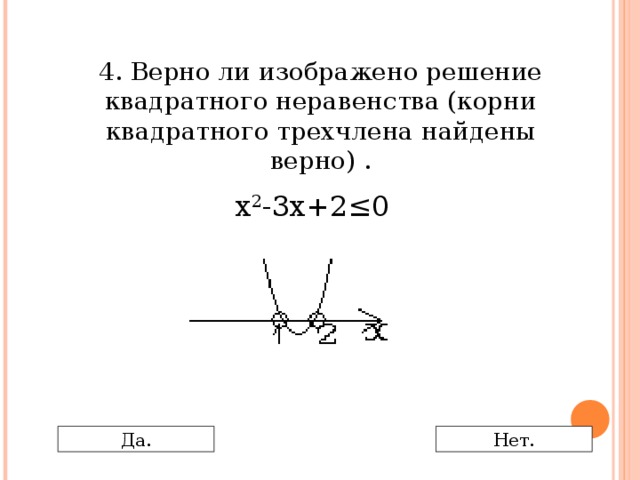
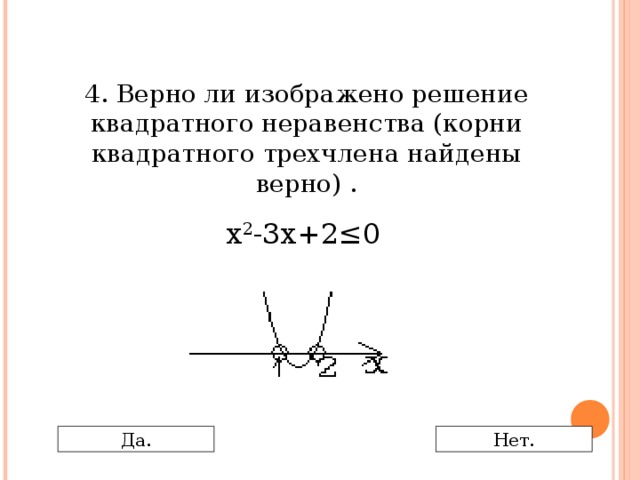
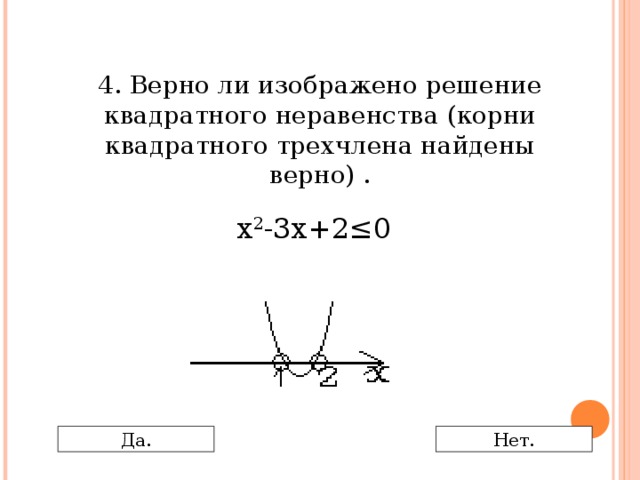
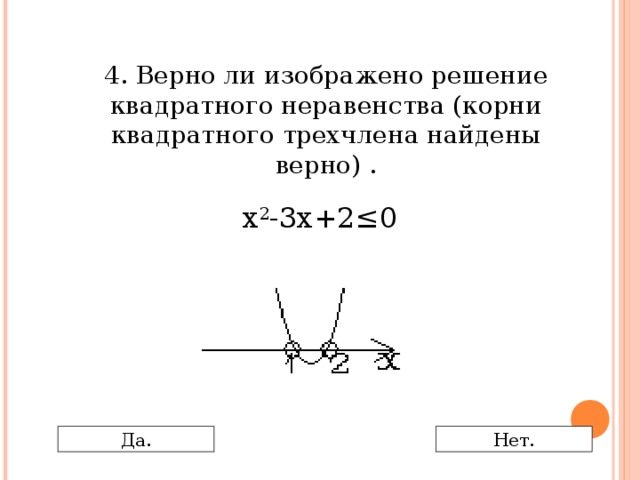
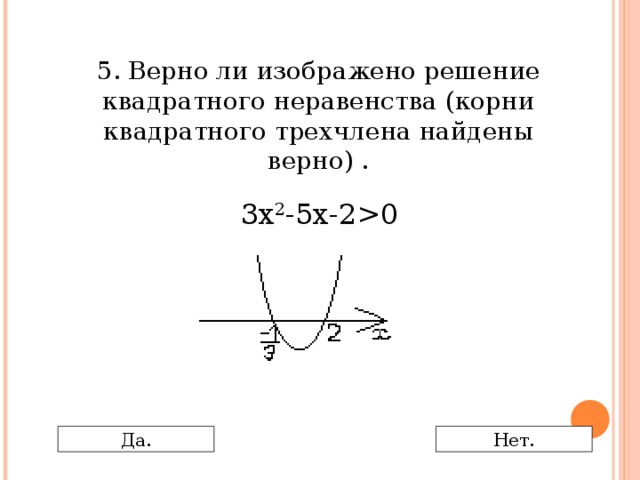 0 Да. Нет." width="640"
0 Да. Нет." width="640"
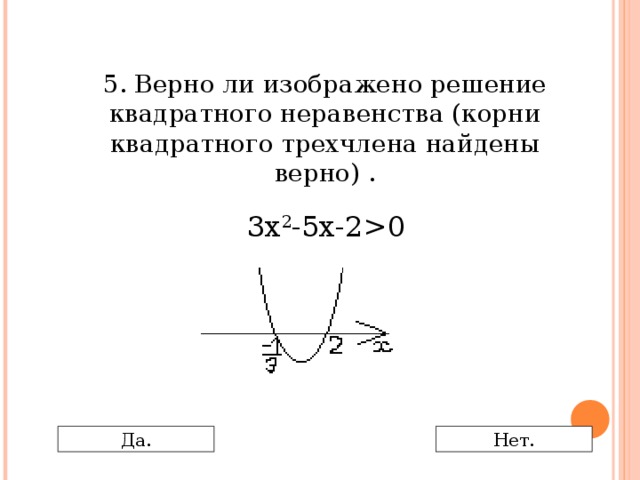 0 Да. Нет." width="640"
0 Да. Нет." width="640"
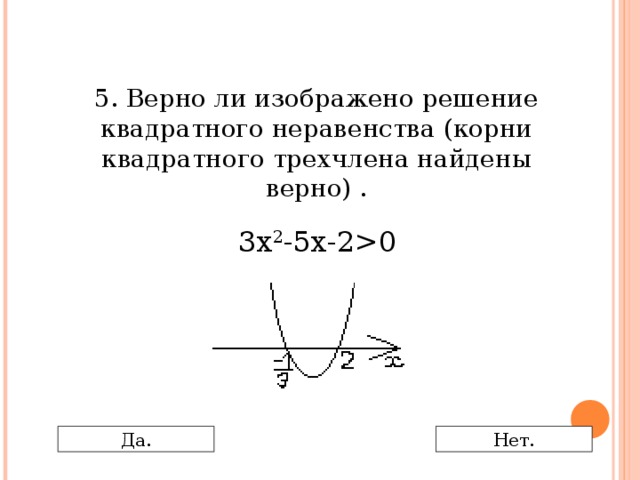 0 Да. Нет." width="640"
0 Да. Нет." width="640"
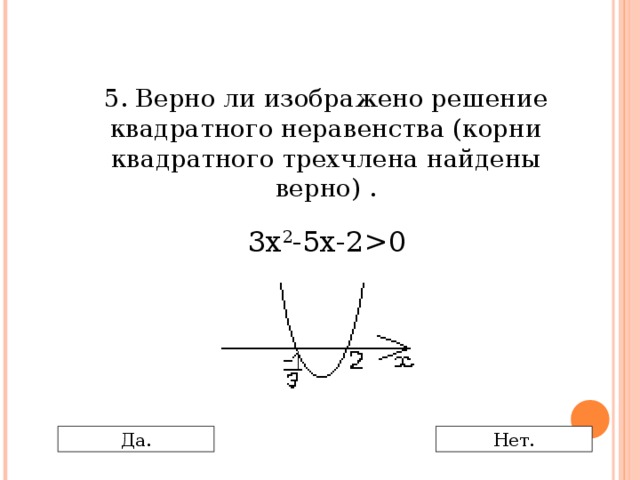 0 Да. Нет." width="640"
0 Да. Нет." width="640"
 0 Да. Нет." width="640"
0 Да. Нет." width="640"






 0 D0 М олодец назад" width="640"
0 D0 М олодец назад" width="640"
 0, Dмолодец назад" width="640"
0, Dмолодец назад" width="640"
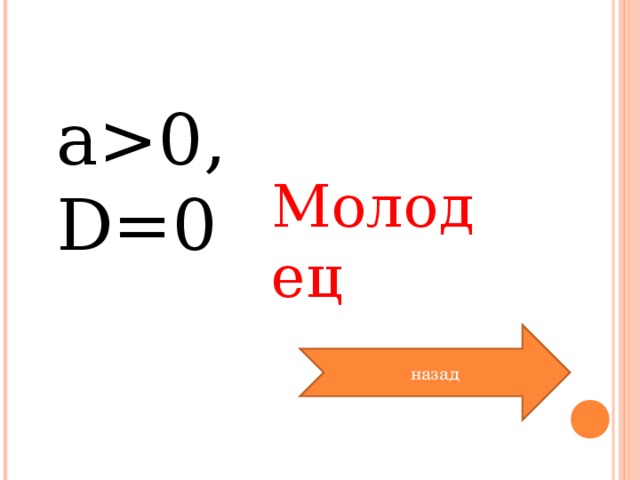 0, D=0 Молодец назад" width="640"
0, D=0 Молодец назад" width="640"
 0 назад" width="640"
0 назад" width="640"


















