В данной презентации присутствует как теоретический материал, так и дидактика по указанной теме.
Урок «Рациональные числа»
(8 класс)
Цели урока:
Создать условия, при которых ученик:
- расширит представления о числе, сформирует понятие «рациональное число»;
- систематизирует знания о числовых множествах;
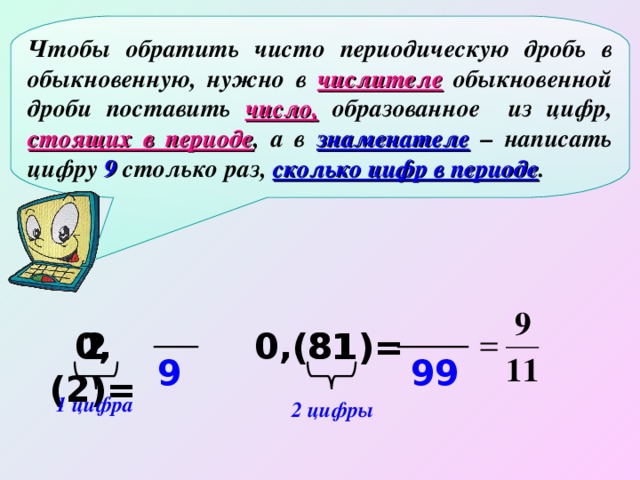
- приобретет навыки перевода рациональных чисел в десятичную (конечную или бесконечную) дробь; бесконечных десятичных периодических дробей в рациональные числа; различные способы перевода бесконечной десятичной периодической дроби в обыкновенную дробь;
- приобретет умения работать в парах,
- разовьет навыки самостоятельной работы, умения анализировать, сравнивать, внимательно выполнять необходимые действия.
В результате ученик:
- знает, как определить вид числа, его принадлежность к числовым множествам;
- умеет правильно пользоваться математической символикой в процессе выполнения заданий;
- умеет представлять рациональное число в виде конечной или бесконечной периодической дроби;
- сможет научиться представлять бесконечную периодическую дробь в виде обыкновенной дроби;
- Организационный этап, повторение ранее изученного.
Приветствие, проверка готовности к уроку, работа в тетради – число, тема урока (слайд).
Учащиеся работают на трех уровнях сложности. Чтобы было проще организовать работу, каждый знает свой «вариант» - уровень.
Ученики получают задание на 3 варианта (от самого простого – базового, потом средний уровень и самый сложный).
как вариант: Тест проходит в режиме on-line по ссылке: http://onlinetestpad.com/ru-ru/Go/Racionalnye-chisla-8-klass-18935/Default.aspx
Я делаю тесты сама в программе INDIGO.
Учащиеся сидят по рядам в соответствии с вариантом, но у них всегда есть право выбора при проверочных работах. Такая форма рассадки хороша тем, что легко организовать работу в парах «равноценных» учеников. Ученики 1 варианта (самый легкий – базовый) работают с учителем - игра «Верю – не верю». У учащихся на бланках распечатаны вопросы. Они точно такие же, как у учителя, но напечатаны вразброс и на отдельных полосках. Задача учеников – найти тот вопрос, который сейчас задал учитель и ответить на него прямо на этом листе. Такая форма объясняется тем, что слабые ученики, как правило – это кинестетики, поэтому для них и добавляется движение во время работы. Учитель зачитывает вопросы в следующем порядке:
Верите ли вы:
- что число -5 - натуральное?
- что натуральные числа использовали для счета предметов?
- что самое маленькое натуральное число – это 0?
- что любое натуральное число (например, 4) можно записать в виде обыкновенной дроби?
- что дроби появились, когда люди стали делить между собой имущество, измерять земельные участки, исчислять время?
- что - это натуральное число?
- что любое целое число (например, -67) можно записать в виде десятичной дроби?
- что знак Î означает «принадлежит»?
- что запись «(3;5) Ì (2;9)» означает «промежуток от 3 до пяти является частью промежутка от 2 до 9»?
- что утверждение «2 Ï Z» - верное?
- что -7 > 0?
- что знак Ë означает «является частью»?
- что - это дробь?
- что дробь и рациональное число – это одно и то же?
- что множество целых чисел – самое маленькое?
Выполнение тестов заканчивается в одно время для всех учащихся (не более 10 минут с учетом орг. момента). 2 и 3 варианты не запускают проверку результатов.
2. Основной этап урока с сообщение нового блока теории и проверки имеющихся знаний.
Далее учитель рассказывает блок теории, в это время ученики должны в это время откорректировать свои ответы или убедиться в их правильности.
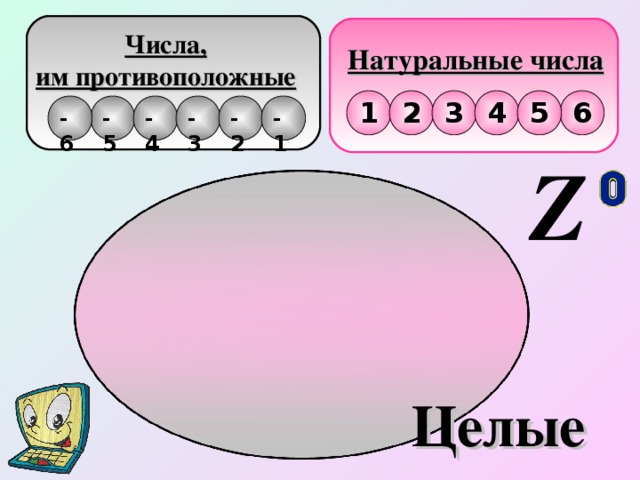
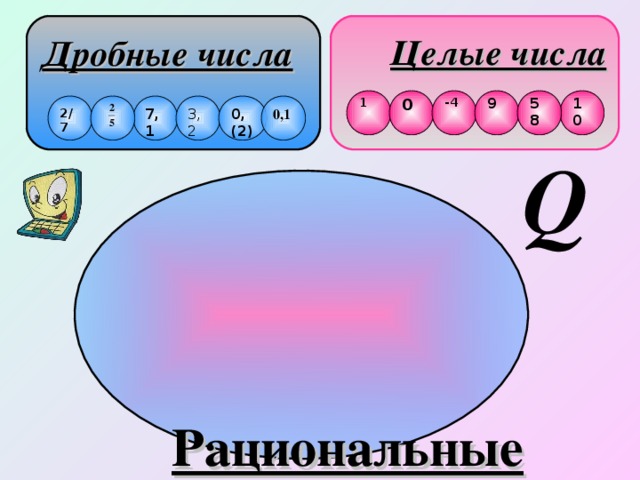
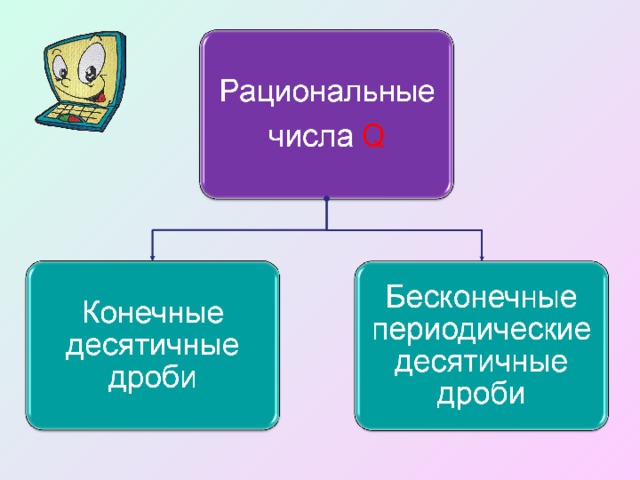
Блок теории – на слайдах и к ним комментарии учителя:
После этого дается время ученикам последний раз просмотреть свои ответы и проверить результаты. Для 1 варианта на слайде появляются правильные ответы. После этого еще раз вопрос: остались ли неправильные ответы и они обсуждаются вслух вместе со всеми учениками.
Следующий блок теории учащиеся фиксируют в тетрадях одновременно с объяснением учителя. Демонстрация идет на слайдах с краткими пояснениями.
3. Рефлексивно-оценочный этап
Теперь необходимо самостоятельно или с помощью соседа по парте или учителя попробовать воспроизвести алгоритмы на конкретных примерах. Работа в парах, по необходимости, с привлечением учителя. Задания для каждого варианта составлены по суммирующему принципу – чем больше решишь, тем выше отметка.
«НА 3»:
1. Определите какое множество является подмножеством множества [8;21]
а) (6;21] б) (9;20) в) [6;21] г) (6;8)
2. Для записи используется математический символ
а) ⊂ б) ∈ в) ∩ г) ∅
3. Отметьте числа -72; 6; -35,13; 106,4 на координатной оси
4. Соотнесите обыкновенные дроби с равными им десятичными.
А. Б. В. Г.
1) 0,5 2) 0,02 3) 0,12 4) 0,625
5. Сравните числа:
а) -5,7 и 0,334 б) 5,(7) и 5, 773
«НА 4»:
6. Переведите в бесконечную периодическую десятичную дробь число
8. Представьте в виде обыкновенной дроби число 1,(72)
«НА 5»:
9. Представьте в виде обыкновенной дроби число 2,9(12)
Работы сдаются учителю. Самопроверка будет осуществлена на следующем уроке после выполнения домашнего задания и повторения теории. Работа обучающего характера, поэтому важна не отметка. а понимание материала.
Подведем итог урока. Какие цели ставились в начале урока? (слайд). В тетради запишите то, в чем вы уверены, что научились делать
Давайте проговорим то, что вы написали:
- знаем, что все числа объединены во множество рациональных чисел;
- умеем пользоваться символикой и определять принадлежность чисел и промежутков;
- умеем любое число представлять в виде дроби , где или в виде бесконечной периодической дроби;
- получили возможность научиться переводить бесконечные периодические дроби в обыкновенные двумя способами, заметили, что второй способ трудно формулировать, но его применение ускорит получение результата).
4. Домашнее задание (презентация и слайды домашнего задания вывешиваются в специально для этого созданной группе в Контакте или фотографируются учащимися).
1. Дана фраза: «28 - рациональное число». Как можно записать иначе?
а) 28 ∈ N б) 28 ∈ Q в) 28 ∈ Z
2. Вычисли значение дроби − d, если a = 13; b = 36; c = 0,9; d=1,76;
3. Утверждение «−17∈(−17;5]» является: а) ложным; б) истинным
4. Выясни при каком наименьшем целом значение p число 3p+15p+2 является целым
5. Вычислить значение выражения:








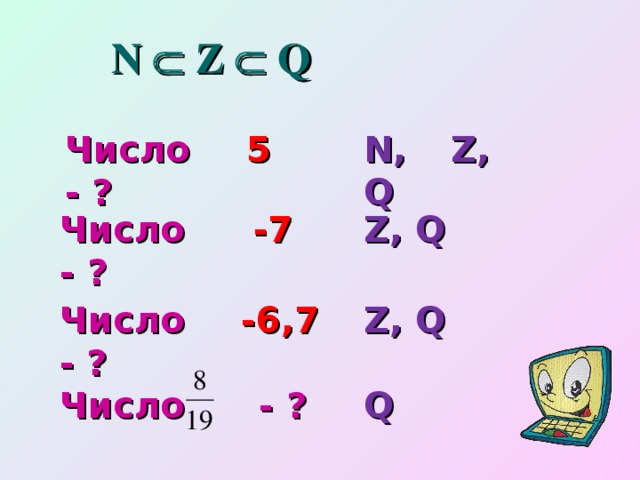












![1. Дана фраза: «28 - рациональное число». Как можно записать иначе? а) 28 ∈ N б) 28 ∈ Q в) 28 ∈ Z 2. Вычисли значение дроби − d, если a = 13; b = 36; c = 0,9; d=1,76; 3. Утверждение «−17∈(−17;5]» является: а) ложным; б) истинным 4. Выясни при каком наименьшем целом значение p число 3p+15p+2 является целым 5. Вычислить значение выражения:](https://fsd.kopilkaurokov.ru/uploads/user_file_548f1fe0e5611/img_user_file_548f1fe0e5611_25.jpg)

















