План урока по теме
«Иррациональные числа»
«Числа не управляют миром,
но они показывают, как управлять им»
И. Гёте
ЦЕЛИ УРОКА:
- Цели обучения:
- расширить представления учащихся о числе, сформировать понятие «иррациональное число»;
- формировать умения различать эти множества чисел и выполнять все арифметические действия;
- систематизировать знания о числовых множествах;
- развитие познавательного интереса через применение занимательных задач и примеров.
2. Цель воспитания:
- воспитание осознанных мотивов учения и положительного отношения к знаниям.
Учебно-методическое обеспечение
? Ю.Н.Макарычев Алгебра. 8 класс: учебник для общеобразовательных учреждений-М.: Просвещение, 2014 г.
?Н.Г. Миндюк Дидактические материалы. Алгебра. 8 класс-М.: Просвещение, 2014г.
? Н.Г. Миндюк Рабочая тетрадь. Часть 1 Алгебра. 8 класс-М.: Просвещение, 2014г.
Необходимое оборудование и материалы для занятий:
Ход урока
- Организационный момент
- Устная работа
- Какую тему мы изучили на прошлом уроке? (Рациональные числа)
- Какие числа называются рациональными? (Числа, которые можно представить в виде дроби m/n, где m-целое число, n-натуральное. Пример 3/5 можно представить разными способами: 3/5=6/10=9/15=……. )
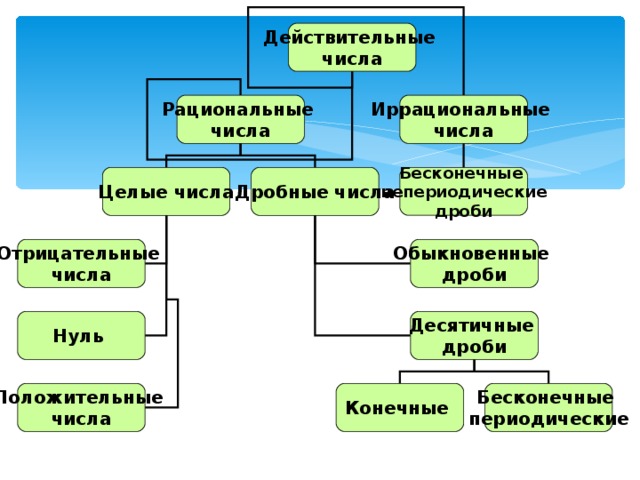
- Какие множества вы уже знаете? (натуральные –N, целые-Z, рациональные – Q,
- Задание на доске: Определите к какому множеству принадлежит каждое из чисел? Заполните таблицу. -7; 19; 3/8; -5,7; 235; -90; -1(4/11); 0,2020020002…; -p.
Натуральные –N
Целые-Z
Рациональные – Q
?
19; 235
-7; 19; 235; -90
-7; 19; 3/8; -5,7; 235; -90; -1(4/11)
А эти числа 0,2020020002…; -p куда следует отнести?
Наших знаний не хватает, чтобы что-то сказать о них. И вот сейчас мы переходим к изучению нового материала, а тема урока «Иррациональные числа», узнаете какие числа называются иррациональными и приведем примеры.
Рассмотрим бесконечную десятичную дробь
Данная бесконечная десятичная дробь по определению не является рациональным.
Значит эта дробь «не рациональное» число.
«НЕ» заменим приставкой «ИР».
Получим «иррациональное» число.
Иррациональное число – десятичная бесконечная периодическая дробь.
Рассмотрим примеры иррациональных чисел.
Иррациональное нельзя представить в виде дроби
где т – целое число, п – натуральное.
Действительные числа можно складывать, вычитать, умножать, делить, сравнивать.
Вернемся к нашей таблице. (Допишем в 4-ю колонку иррациональные числа и 0,2020020002…; -p
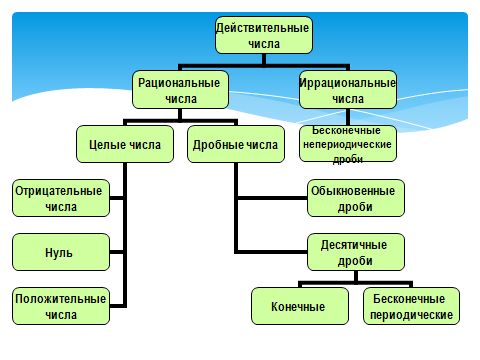
Обобщим знания о всех множествах чисел
Закрепление
Все задания из учебника можно разбить на 2 группы.
1-я – задания на определение принадлежности к различным числовым множествам.
2-я – задания на сравнение действительных чисел.
Выполним номера: №276, 277, 279, 287.(устно)
Выполним номера: № 280, 283, 288 (у доски)
Тест с последующей проверкой
«+» - согласен с утверждением; «-» - не согласен с утверждением.
1) Всякое целое число является натуральным.
2) Всякое натуральное число является рациональным.
3) Число -7 является рациональным.
4) Сумма двух натуральных чисел всегда является натуральным числом.
5) Разность двух натуральных чисел всегда является натуральным числом.
6) Произведение двух целых чисел всегда является целым числом.
7) Частное двух целых чисел всегда является целым числом.
8) Сумма двух рациональных чисел всегда является рациональным числом.
9) Частное двух рациональных чисел всегда является рациональным числом.
10) Всякое иррациональное число является действительным.
11) Действительное число не может быть натуральным.
12) Число 2,7(5) является иррациональным.
13) Число p является действительным.
14) Число 3,1(4) меньше числа p.
15) Число - 10 принадлежит одновременно множеству целых, рациональных и действительных чисел.
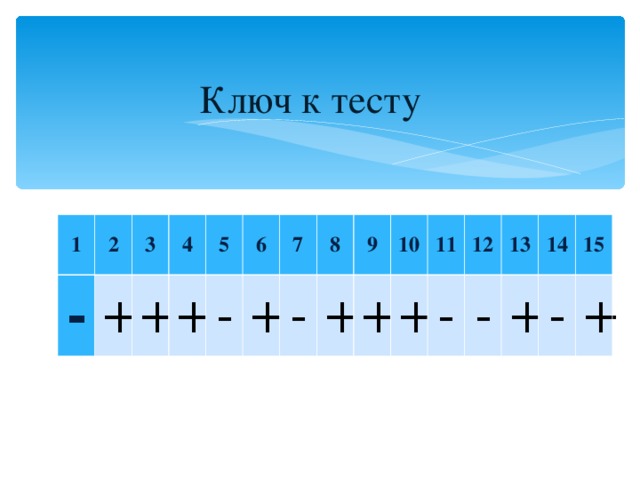
Ключ:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
-
+
+
+
-
+
-
+
+
+
-
-
+
-
+
Оценка
15 правильных ответов – оценка «5»
12-14 правильных ответов – оценка «4»
8-11 правильных ответов - оценка «3»
менее 8 следует подучить теорию.
Рефлексия
Какие числа называются рациональными, иррациональными?
Из каких чисел состоит множество действительных чисел?
Домашнее задание
п. 11 Прочитать.
№278; 281; 282
Оценки за урок.
Спасибо за урок!
Просмотр содержимого документа
«План»
Муниципальное бюджетное общеобразовательное учреждение
«Тургеневская СОШ»
Учитель: Лойко Галина Алексеевна
План урока по теме
«Иррациональные числа»
«Числа не управляют миром,
но они показывают, как управлять им»
И. Гёте
ЦЕЛИ УРОКА:
Цели обучения:
расширить представления учащихся о числе, сформировать понятие «иррациональное число»;
формировать умения различать эти множества чисел и выполнять все арифметические действия;
систематизировать знания о числовых множествах;
развитие познавательного интереса через применение занимательных задач и примеров.
2. Цель воспитания:
Учебно-методическое обеспечение
● Ю.Н.Макарычев Алгебра. 8 класс: учебник для общеобразовательных учреждений-М.: Просвещение, 2014 г.
●Н.Г. Миндюк Дидактические материалы. Алгебра. 8 класс-М.: Просвещение, 2014г.
● Н.Г. Миндюк Рабочая тетрадь. Часть 1 Алгебра. 8 класс-М.: Просвещение, 2014г.
Необходимое оборудование и материалы для занятий:
Ход урока
Организационный момент
Устная работа
Какую тему мы изучили на прошлом уроке? (Рациональные числа)
Какие числа называются рациональными? (Числа, которые можно представить в виде дроби m/n, где m-целое число, n-натуральное. Пример 3/5 можно представить разными способами: 3/5=6/10=9/15=…….. )
Какие множества вы уже знаете? (натуральные –N, целые-Z, рациональные – Q,
Задание на доске: Определите к какому множеству принадлежит каждое из чисел? Заполните таблицу. -7; 19; 3/8; -5,7; 235; -90; -1(4/11); 0,2020020002…; -.
| Натуральные –N | Целые-Z | Рациональные – Q | ? |
| 19; 235 | -7; 19; 235; -90 | -7; 19; 3/8; -5,7; 235; -90; -1(4/11) |
|
А эти числа 0,2020020002…; - куда следует отнести?
Наших знаний не хватает, чтобы что-то сказать о них. И вот сейчас мы переходим к изучению нового материала, а тема урока «Иррациональные числа», узнаете какие числа называются иррациональными и приведем примеры.
Рассмотрим бесконечную десятичную дробь
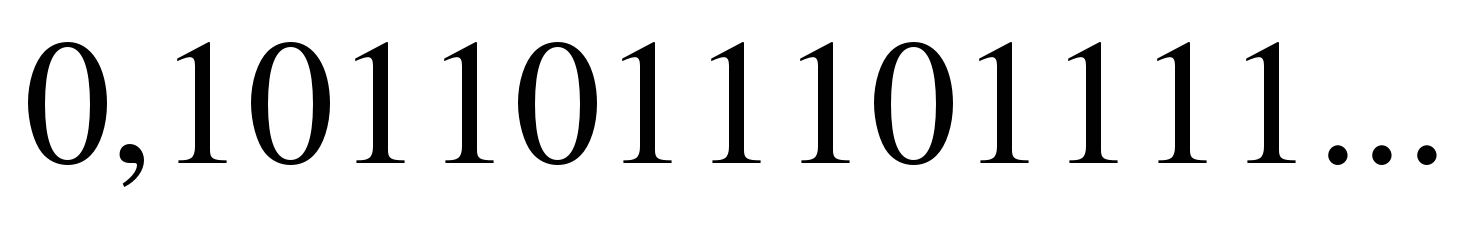
Данная бесконечная десятичная дробь по определению не является рациональным.
Значит эта дробь «не рациональное» число.
«НЕ» заменим приставкой «ИР».
Получим «иррациональное» число.
Иррациональное число – десятичная бесконечная периодическая дробь.
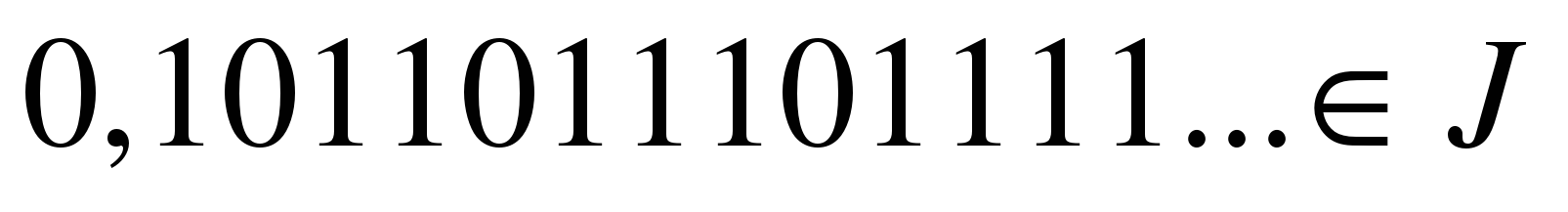
Рассмотрим примеры иррациональных чисел.
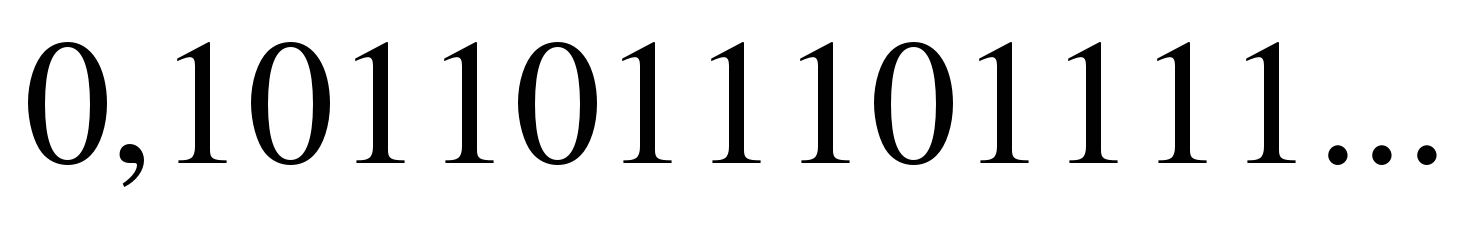
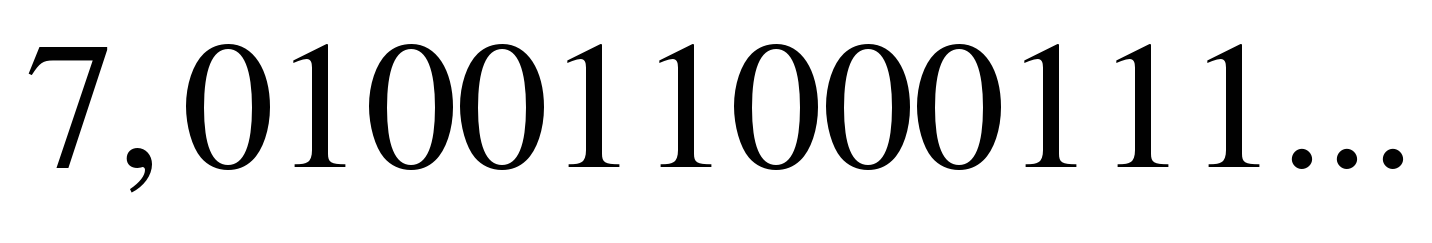
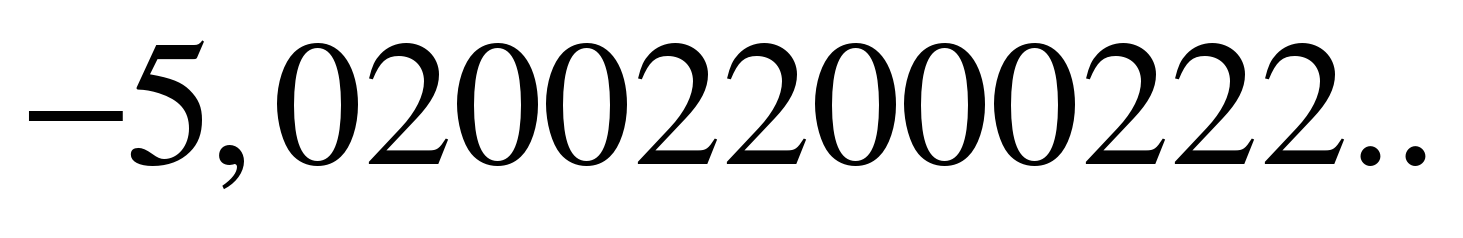
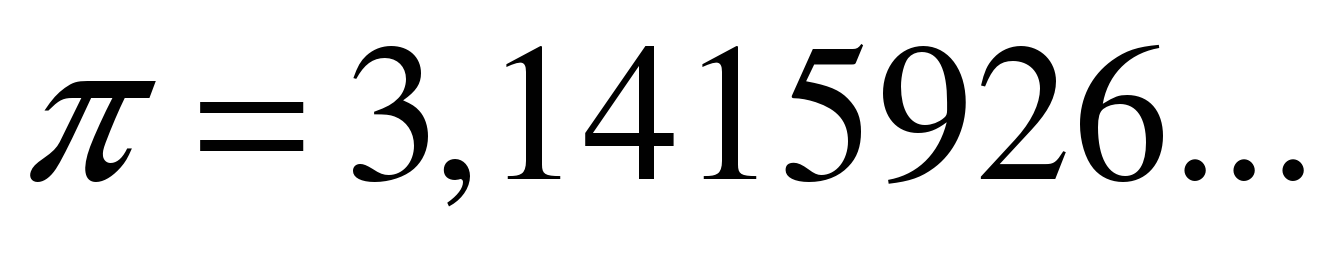
Иррациональное нельзя представить в виде дроби
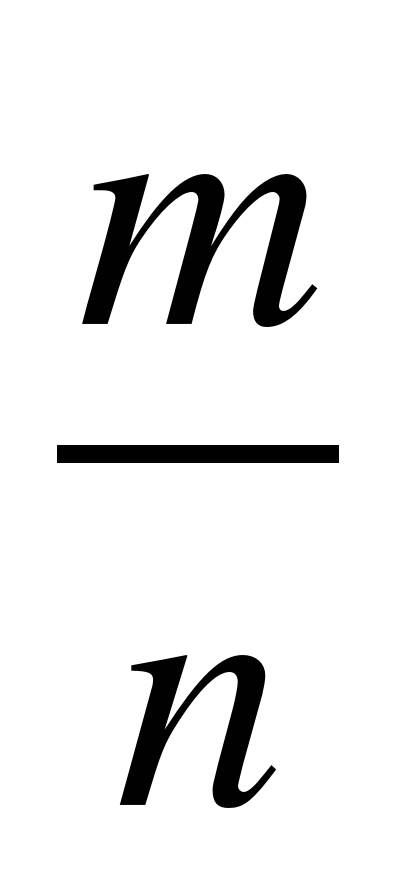где т – целое число, п – натуральное.
Действительные числа можно складывать, вычитать, умножать, делить, сравнивать.
Вернемся к нашей таблице. (Допишем в 4-ю колонку иррациональные числа и 0,2020020002…; -
Обобщим знания о всех множествах чисел
Закрепление
Все задания из учебника можно разбить на 2 группы.
1-я – задания на определение принадлежности к различным числовым множествам.
2-я – задания на сравнение действительных чисел.
Выполним номера: №276, 277, 279, 287.(устно)
Выполним номера: № 280, 283, 288 (у доски)
Тест с последующей проверкой
«+» - согласен с утверждением; «-» - не согласен с утверждением.
1) Всякое целое число является натуральным.
2) Всякое натуральное число является рациональным.
3) Число -7 является рациональным.
4) Сумма двух натуральных чисел всегда является натуральным числом.
5) Разность двух натуральных чисел всегда является натуральным числом.
6) Произведение двух целых чисел всегда является целым числом.
7) Частное двух целых чисел всегда является целым числом.
8) Сумма двух рациональных чисел всегда является рациональным числом.
9) Частное двух рациональных чисел всегда является рациональным числом.
10) Всякое иррациональное число является действительным.
11) Действительное число не может быть натуральным.
12) Число 2,7(5) является иррациональным.
13) Число является действительным.
14) Число 3,1(4) меньше числа .
15) Число - 10 принадлежит одновременно множеству целых, рациональных и действительных чисел.
Ключ:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| - | + | + | + | - | + | - | + | + | + | - | - | + | - | + |
Оценка
15 правильных ответов – оценка «5»
12-14 правильных ответов – оценка «4»
8-11 правильных ответов - оценка «3»
менее 8 следует подучить теорию.
Рефлексия
Какие числа называются рациональными, иррациональными?
Из каких чисел состоит множество действительных чисел?
Домашнее задание
п. 11 Прочитать.
№278; 281; 282
Оценки за урок.
Спасибо за урок!
Просмотр содержимого документа
«Тест с последующей проверкой»
Тест с последующей проверкой
«+» - согласен с утверждением;
«-» - не согласен с утверждением.
1) Всякое целое число является натуральным.
2) Всякое натуральное число является рациональным.
3) Число -7 является рациональным.
4) Сумма двух натуральных чисел всегда является натуральным числом.
5) Разность двух натуральных чисел всегда является натуральным числом.
6) Произведение двух целых чисел всегда является целым числом.
7) Частное двух целых чисел всегда является целым числом.
8) Сумма двух рациональных чисел всегда является рациональным числом.
9) Частное двух рациональных чисел всегда является рациональным числом.
10) Всякое иррациональное число является действительным.
11) Действительное число не может быть натуральным.
12) Число 2,7(5) является иррациональным.
13) Число является действительным.
14) Число 3,1(4) меньше числа .
15) Число - 10 принадлежит одновременно множеству целых, рациональных и действительных чисел.
Ответы
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценка
15 правильных ответов – оценка «5»
12-14 правильных ответов – оценка «4»
8-11 правильных ответов – оценка «3»
менее 8 – следует подучить теорию.
Просмотр содержимого презентации
«Презентация»
